基于IACO-PF的锂电池SOC估算

单成鑫，李立伟，杨玉新

（1青岛大学电气工程学院；2青岛大学威海创新研究院；3青岛大学图书馆，山东 青岛266071）

近年来，能源危机和环境污染的影响，使得电动汽车的研究和应用实现了迅速发展[1]。锂离子电池凭借能量比高、寿命长、自放电率低的特点，在电动汽车领域得到了广泛应用。由于锂离子电池的失效可能会导致严重的后果，为了保障电池的安全应用，提出了一种对电池状态进行实时监控的电池管理系统[2](battery management system，BMS)。电池荷电状态[3](state of charge，SOC)是BMS 的重要参数，由于SOC 是电池的内部状态，不能直接测量。因此，SOC的估计成为了许多研究者的关注的问题，目前已经提出了许多估计方法，可以分为三大类：开环法、数据驱动法和基于模型的方法[4]。开环法包括安时积分法和开路电压法，数据驱动的方法主要包括神经网络[5]模糊算法，卡尔曼滤波[6]和粒子滤波[7](particle filter，PF)是基于模型方法中常见的算法。上述估算方法的优缺点见表1。

表1 电池SOC估算方法的优缺点Table 1 Advantages and disadvantages of battery SOC estimation method

PF 是一种高精度的基于概率的估计算法，PF利用蒙特卡洛方法采样的一组加权粒子来近似系统的后验分布，对分布的形式没有任何明确的假设，该方法适用于具有较强非线性[8]的复杂模型的状态估计。对于非高斯分布系统噪声条件下具有复杂形式的非线性锂离子电池模型，利用PF 进行荷电状态估计，具有更好的优势。传统PF 算法在迭代求解的过程中，往往会出现粒子多样化降低，产生粒子贫化现象，造成估算结果产生较大误差降低算法的估计精度[9]。近年来智能优化算法在处理优化问题中具有独特优势，可以用于解决粒子滤波粒子贫化的问题[10]。蚁群算法(ant colony optimization，ACO)是一种类似于遗传算法的迭代优化方法[11]。该算法在许多领域都有良好的优化性能，在PF 算法过程中，采用ACO 算法在更新步骤之前对粒子分布进行优化，从而使粒子贫化问题最小化。本文采用改进ACO算法，通过改进传统ACO算法中的信息素浓度和启发式的相对影响参数以及信息素挥发速率，解决该算法的局部最优问题，再对PF 进行优化，改善PF中粒子贫化问题。

1 电池模型及参数辨识

1.1 锂离子电池模型

等效电路模型的建立，不仅考虑其精确性，也要兼顾复杂性。电池的充放电动态性能由RC 环节描述，并且考虑了电池的极化现象。随着更多RC环节的累积，模型更准确，但更复杂。考虑到模型的精确性和简单性，选择二阶Thevenin 电池等效模型来描述锂离子电池。模型电路如图1 所示，UOC为电池开路电压；R0表示电池欧姆内阻；UL为负载电压；R1、R2、C1、C2为极化内阻、极化电容；I为电路中流过的电流，两个RC环节的环路电压分别为U1、U2。

图1 二阶Thevenin等效模型Fig.1 Second-order Thevenin equivalent model

电池SOC 选取安时积分法进行计算，并根据基础电路定律，对等效电路模型进行分析，可列出以下关系式

式中，SOC0表示为SOC 的初始值；I 表示瞬时电池端电流，在放电过程中被认为是正的，充电过程则为负；t 为时间；η 为库仑效率；QN为电池额定容量；UL、I由试验测量得出。

对式(1)～(3)进行离散化处理，选取SOC作为状态变量，电池端电压UL作为观测变量，得到电池的非线性状态空间模型。

状态方程

观测方程

式(5)中

式中，∆t 为采样间隔；ω、v 为过程和观测噪声；UOC(SOCt)所表示的UOC与SOC 的函数拟合关系以及两个RC环节中R1、C1、R2、C2参数，将由下一节的参数辨识给出。

1.2 参数辨识

锂电池的测试平台由直流电子负载、dSPACE MicroLabBox试验箱以及计算机组成。本次试验采用额定电压3.7 V，额定容量为1.5 A·h的锂电池组在室温25°C下进行测试。对选取的二阶Thevenin电池等效模型通过试验测得的数据采用指数拟合方法进行参数辨识[12]。

首先将电池充满电后静置1 h，测得开路电压。然后采用1 C的间歇脉冲电流对电池进行放电180 s，然后静置180 s，间歇周期为360 s。每次放电过程，电池的SOC减少5%。并将静置结束时的电压值记录下来，近似为开路电压。放电过程中电压的部分曲线变化如图2所示。

图2 脉冲放电电压部分波形Fig.2 Partial waveform of pulse discharge voltage

通过图2 可以发现在放电过程中，在AB 段与CD段电池电压出现了跳跃式突变，由等效电路图可知，C1、C2端电压不会突变，这是因为电池本身欧姆内阻造成的。在BC段与DE段电池电压则出现了指数式缓慢变化，这是因为电池内部的极化现象造成的，对应等效电路图中两个RC环节影响的结果。

结合脉冲放电试验数据，对电池欧姆内阻与RC环节进行参数辨识。在这里对于欧姆内阻R0的值，选取如图CD 段电池放电结束时突变的压降与放电电流之比，即

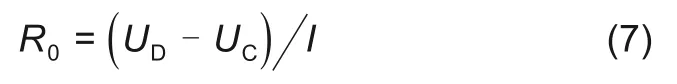
在脉冲放电后的静置时间段中(DE 段)，RC 环节可看作零输入响应，电池的输出方程为

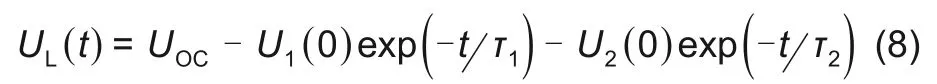
U1(0)为R1C1在放电结束瞬间电压初始值，U2(0)为放电的初始值。在MATLAB的Curve Filting工具箱中利用式(8)跟DE段电压数据曲线拟合，求出时间常数τ1、τ2。在脉冲放电过程中BC 段，两个RC环节可看作为零状态响应，电池的输出方程为

将上一步通过拟合求得的时间常数τ1、τ2代入，再次使用MATLAB Curve Filting 工具箱利用式(9)跟BC段电压数据曲线拟合，得出R1、R2，再根据τ1=R1C1，τ2=R2C2，分别求出C1、C2。

参数辨识结果见表2。

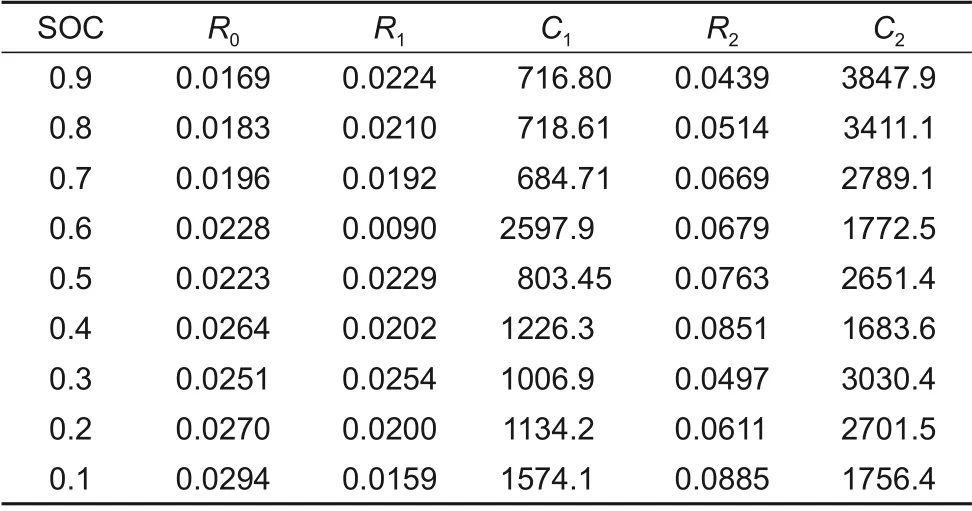
表2 二阶模型辨识参数Table 2 Second-order model identification parameter

1.3 OCV-SOC拟合

根据1.2 节记录的放电试验过程中的近似开路电压，以及对应SOC 值的试验数据。在MATLAB中的cftool 工具箱进行7 次多项式的曲线拟合，得到开路电压UOC与SOC的函数关系式

7次拟合曲线方程的判定系数为0.9997，效果较好。既能保证拟合精度，又能减轻后续运行负担。

2 PF算法

粒子滤波是基于蒙特卡洛方法递推的贝叶斯滤波[13]，通过一组随机样本表示所需的状态概率分布，并给出解决贝叶斯估计问题的方法。它通过一组加权粒子来逼近后验，其形式没有任何明确的假设，因此可以用于任何非线性非高斯系统。

首先，需要求得后验分布的最优贝叶斯解。假设用于贝叶斯估计的状态值(xk)和观测值(yk)由以下方程式控制。

式中，fk为先前状态xk和状态噪声ωk的非线性函数；hk为状态xk和观测噪声vk的非线性函数；ωk、vk为相互独立的系统状态和观测噪声。假设初始状态p(x0)概率密度函数已知，贝叶斯估计目的是递归计算每个状态xk的后验概率密度p(xk|y1:k)。

假设系统状态服从一阶马尔可夫系统模型，得到先验概率分布的一般表达式，再由此求出后验概率分布

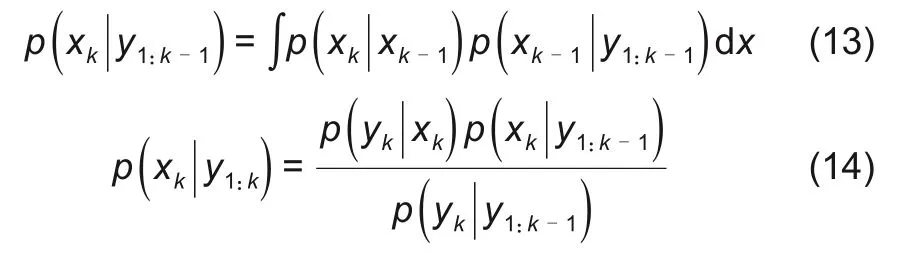
上式中，分母是一个常数值

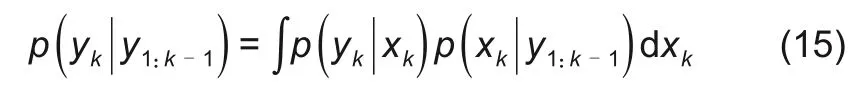
式(13)和式(14)的递归关系构成了最佳贝叶斯解的基础。但是，后验概率密度的这种递归传播在理论上只是一个最佳解决方案，而且由于式(13)中的积分通常很难处理，因此无法通过求解获得。所以在粒子滤波算法中使用蒙特卡洛模拟和重要性采样执行递归贝叶斯估计，假设已知重要性概率密度函数q(xk|yk)，从中采样抽取粒子集{xi0:k}Ni=0，x0:k={xj,j=0,1…,k}，是0～k时刻的状态集，其对应权值{wik}Ni=0更新式如下

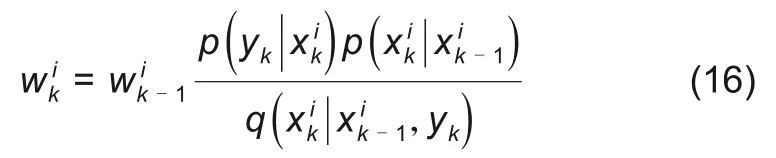
将权值归一化得到下式

其中后验密度通过状态空间附近的粒子的相对密度来近似

其中δ(∙)为狄拉克函数。当N足够大时，近似值(18)就越接近真实后验密度p(xk|y1:k)。

粒子滤波的具体实现步骤如下。

（1）初始化状态：从先验概率分布p(x0)中随机选取N 个初始状态粒子xi0，i=(1,2,...N)，并将特定粒子的初始粒子权重指定为1/N。粒子数量取决于系统类型和计算成本。重采样的阈值可以初始化为Nth=2N/3。

（2）重要性采样：使用状态方程更新状态值，并根据式(16)更新粒子权重。

（3）权重归一化：使用式(17)将所有粒子的总权重归一化。

（4）重采样：重采样的阈值定义为有效样本Neff，可以将其定义为

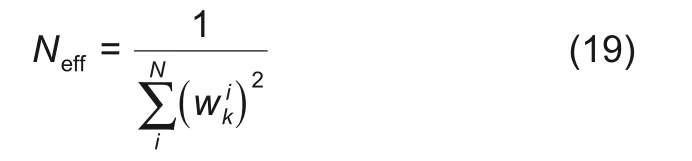
如果有效粒子低于给定的Nth，则对粒子重新采样以得到权重为1/N的新粒子。

（5）状态估计：将状态计算为

3 IACO-PF算法

3.1 ACO算法

蚁群算法本质上是一个基于生物的系统，该系统基于模拟蚂蚁自然行为的媒介[14]。ACO源自蚂蚁展示的自然优化能力。当寻找食物时，它们倾向于沿着巢穴i 和一些外部地标j 之间的最佳路线(或路径)前进，因为如果更多的蚂蚁选择相同的路径，它们的特定信息素浓度τij就会变得更高。地标离巢穴越近，蚂蚁可进行的往返次数就越高。信息素浓度τij越高，更多的蚂蚁会选择这种途径而不是其他可能的途径。该迭代过程实现了端点之间的最佳路径。因此，ACO 算法使用数学公式来模拟此自然优化过程。蚂蚁k(k=1,2,...,m)的移动方向基于式(21)中定义的概率函数。当一只蚂蚁尚未完成移动时，式(21)用于确定要采取的下一条路径，直到它们收敛到最佳解。

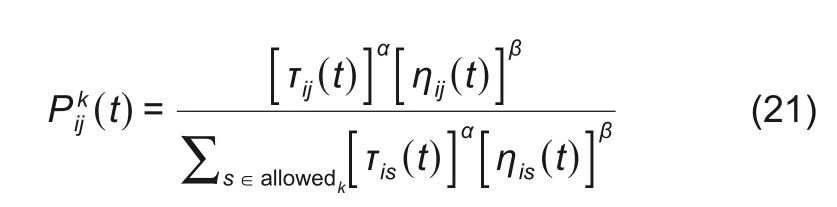
式中，allowedk为可供选择地标的集合；ηij是可作为先验启发式值，定义为i、j 两点间距离dij的倒数，ηij(t)=1/dij。该概率分布受参数α 和β 的偏倚影响，这些参数分别确定信息素浓度和启发式信息的相对影响。

完成一次循环后，信息素浓度τij(t)受蚂蚁的运动影响，根据下式更新

式中，ρ是信息素挥发速率；∆τij(t)为此期间信息素浓度的增强值。

一般来说，ACO算法按照以下规则工作[15]。

（1）对于给定的问题，其候选解与对应于蚂蚁正在访问的路径或顶点相关联。例如，在PF 框架中，如果一个粒子被认为是一只蚂蚁，那么，这个粒子(蚂蚁)就会在状态空间中沿着一条路径运动，最终到达它的新状态。具有新状态的粒子被视为顶点。于是新粒子集形成候选解。

（2）当蚂蚁沿着一条路径移动时，沿着该路径的信息素浓度以一定的水平增加。

（3）当蚂蚁需要在两条或多条路径中选择移动时，往往信息素浓度较高、距离较短的路径被蚂蚁选择的概率较大。

（4）信息素浓度会随着时间的推移而蒸发，这一特性会使蚂蚁最多的路径始终保持信息素的最高水平。

3.2 IACO算法

3.2.1 调整信息素浓度与启发式相对影响参数

在计算转移概率Pkij时，信息素浓度τij随着迭代次数的增加而累积，使得τij的影响逐渐增大，期望启发式的影响逐渐减小，传统蚁群算法往往会陷入局部最优。参数的选择直接影响模型求解的速度和效率。传统蚁群算法中信息素浓度与启发式相对影响参数α、β 一般取1、2.5，为提高ACO 的效率，定义α、β为

式中，Nc为当前迭代次数。α 随着迭代次数的增加逐渐减小，使得τij的影响逐渐降低，同时β 随着迭代进行而逐渐增加，从而增加期望启发式的影响，避免算法陷入局部最优。

3.2.2 改进信息素挥发速率

蒸发速率ρ 的选择对算法的性能有很大的影响。ρ太小会导致信息素的快速积累。因此，也会很容易使该算法陷入局部最优。ρ过大会降低算法的效率。为了提高解的质量，提出了非线性增量蒸发率。ρ的新的更新公式定义为

式中，ρ0为初始定义信息素挥发速率；Nc,max为最大迭代次数。

4 IACO-PF算法设计

4.1 算法思想

为了解决传统粒子滤波中粒子多样性贫化现象，优化粒子滤波的重采样步骤，在更新步骤之前，采用改进的蚁群优化算法[16]。在此之中，蚂蚁将替代随机生成的粒子，它们将根据下面的蚁群算法重新定位，以便在重采样步骤中接近最优解。

在迭代过程中，τij受每次粒子运动的影响，其值的增加或减少取决于粒子j是否位于运动路径中，如下式所示

信息素路径定义意味着路径中信息素浓度会随着更多蚂蚁通过同一路径时而增加，而较少蚂蚁经过的路径的信息素浓度将随时间成比例下降。蚂蚁沿着路径行进并再次返回所花费的时间越长，信息素的蒸发量就越大。相比之下，由于大多数蚂蚁最终选择了该路径，因此信息素的浓度在最短路径中保持较高。

优化步骤基于从式(28)获得的概率函数迭代运行。它表示粒子i在N−1个粒子中选择粒子j作为移动方向的概率。

启发式函数ηij现在定义为两个粒子间距离的倒数

参数τij的初始值为目标粒子j的权重，即

因此，目标粒子j的权值越大，则粒子i向目标粒子j移动的概率就越大，反之越小。α和β是与原始ACO 中定义的参数相同的参数，在粒子滤波中定义为确定权值信息和位置信息的相对影响。

当Pij接近1 时，IACO 算法会收敛，这意味着粒子i会重新定位到粒子j的更近距离处。当在每次迭代过程中都保持这种收敛性时，大多数粒子会收敛到该粒子j，它表示为基于Pij的可能性更高(权重更高)的邻域。如果直接通过概率式(28)将粒子向最优权值的粒子转移，经过多次迭代后会导致粒子多样性降低。因此，本文引入距离阈值λL和概率阈值λP来控制较优权值粒子间的转移。IACO 算法直到所有移动的粒子的位置收敛到在式(31)中定义的距离阈值内的高似然区域(一般或局部最优解)时终止。概率阈值的具体取值通过试验获得。

式中，wj是目标粒子j的权重；randn是正态分布的随机数。

4.2 算法步骤

PF 算法将根据以下步骤重新定位，以便在重采样步骤时接近最优解。

（1）初始化粒子状态。从先验概率分布p(x0)中随机选取N 个SOC 初始状态粒子{SOCi0,i=1,2,...,N},粒子的初始权重大小{wik}N

i=0=1/N。

（2）重要性采样。根据系统状态方程更新粒子，得到下一时刻先验粒子{SOCik,i=1,2,...,N}，并根据下列方程更新粒子权重

（3）采用改进蚁群算法优化粒子状态，当粒子与其目标粒子之间的距离不在阈值λL内，并且迭代时间不超过最大值，则选择距离在阈值λL以内的粒子i根据概率Pij选择移动目标j，设置概率阈值λP，当Pij<λP时，粒子位置保持不变，当Pij>λP时，粒子i转移至目标粒子j位置。之后更新ACO的参数(如η、τ等)。

（4）权重归一化。将采样到的N个粒子的权重进行归一化，得到

（5）重采样。根据有效粒子数Neff比较重采样的阈值，判断是否进行重采样。

（6）状态输出。

5 实验设计与结果分析

5.1 脉冲放电试验

为了验证本文提出的IACO-PF 算法的准确性和有效性，首先根据电池在1C 脉冲放电状态的试验数据以及辨识参数，并代入电池模型的状态方程(4)与观测方程(5)中，分别采用IACO-PF算法和PF算法对锂离子电池进行SOC 估算，并将这两种算法的预测SOC值与真实SOC值进行比较。

各算法均采用过程噪声方差Q=1，观测噪声R=0.01，并取SOC 的初始值SOC0=100，采用粒子数N=100，有效粒子阈值Nth=2N/3。IACO-PF算法中取最大迭代次数Nc,max=100，ρ0=0.5，概率阈值取λP=0.0025。试验得到SOC估算结果以及误差如图3和图4所示。

图3 SOC试验仿真曲线Fig.3 Experiment simulation curve of SOC

图4 SOC试验仿真曲线误差Fig.4 Experiment simulation curve error of SOC

为了更直观地对比两个算法的SOC估算性能，分别计算了两种算法的均方根误差和最大绝对误差来评估预测结果

从图3、图4可以看出，由IACO-PF算法与PF算法得到的SOC预测值都与SOC的真实值非常接近，说明了这两种算法都能对电池的SOC 值做出很好的预测。并且从表3中的数据得出IACO-PF算法和PF算法的SOC预测值与真实值的最大误差都能控制在2.5%以内，说明了对于非高斯分布系统噪声条件下的非线性锂离子电池SOC 的估算，粒子滤波算法具有较强的适用性。从图4可以直观看出，PF 算法由于产生了粒子贫化问题，使得SOC的估计误差开始增大，反观IACO-PF 算法在整个预测过程中误差值都能保持稳定，并且最大误差减小到了1%以内，由此可以说明IACO-PF算法具有更高的有效性和准确性。

表3 两种算法的数据统计Table 3 Data statistics of two algorithms

5.2 DST工况试验

模拟电动汽车实际行驶过程中电流变化情况，并进一步验证IACO-PF 算法的准确性，进行DST方法对电池进行充放电仿真试验[17]，DST工况电流如图5所示，试验前先将电池充分静置，试验参数不变，仿真时间15000 s，试验得到SOC估算结果以及误差如图6和图7所示。

图5 DST工况电流分布图Fig.5 DST operating current profile

图6 SOC试验仿真曲线Fig.6 Experiment simulation curve of SOC

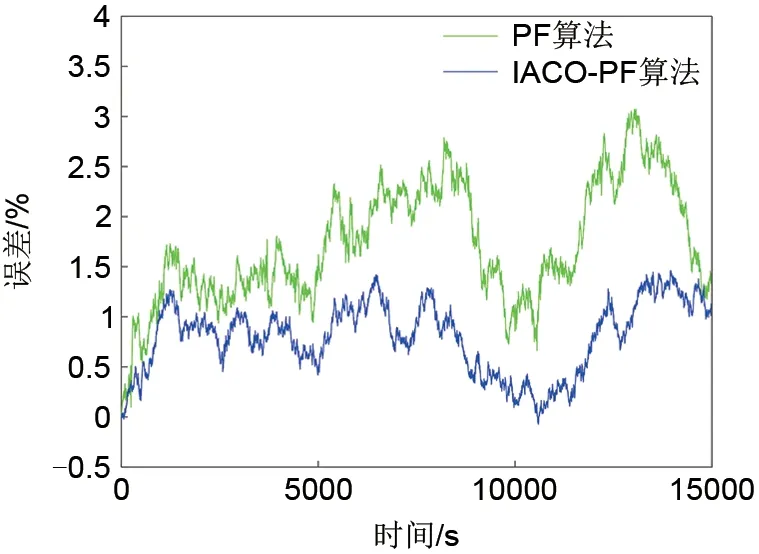
图7 SOC试验仿真曲线误差Fig.7 Experiment simulation curve error of SOC

从图6、图7可知，在DST工况电流下，IACOPF算法与PF算法得到的SOC预测值同样也能很好地趋于SOC真实值，做出良好的预测。由表4中的数据可知，在复杂的工况电流下，两种算法的精度会相应降低，但相比于PF 算法，IACO-PF 算法的SOC估计值仍保持良好的有效性和准确性。

表4 两种算法的数据统计Table 4 Data statistics of two algorithms

6 结 论

结合二阶Thevenin 电池等效模型搭建锂电池状态方程，对传统蚁群优化算法进行调整信息素浓度与启发式相对影响参数以及改进信息素挥发速率来解决传统粒子滤波的粒子贫化问题。试验结果表明，基于IACO-PF 算法的SOC 估计结果相比传统PF 算法更具准确和稳定，对锂电池健康管理具有重要意义。扩展了智能算法SOC估计的研究领域，具有广泛的应用价值。