基于热-电-磁场耦合的高温蓄热导体结构分析

2021-05-26田艳丰赵鑫鑫付启桐赵旭章

储能科学与技术 2021年3期

田艳丰，赵鑫鑫，付启桐，王哲，赵旭章

（1沈阳工业大学电气工程学院，辽宁沈阳110870；2新疆互力佳源环保科技有限公司，新疆乌鲁木齐830022）

根据近几年统计，我国清洁能源发展迅速，其装机容量、发电量已位居世界首位。同时却步入“三弃”(弃风、弃光、弃水)消纳难的困境[1-4]。而利用弃风电在夜间电负荷低谷、热负荷较大时段为大容量高温高电压固体蓄热装置提供能源，不仅可以消纳富余电量，还有利于优化电网负荷曲线，实现削峰填谷，提高电网运行安全性、可靠性，缓解电网调峰压力和供热矛盾[5-8]。高温高电压固体蓄热装置的蓄热功能主要通过由蓄热材料组成的蓄热体和由电热合金制成的加热元件实现。储热材料可以在特定的条件下将热量以材料的热焓贮存起来，并能在需要时释放和利用；电热合金能通过焦耳热对蓄热体进行加热，将无法储存的电能转换为热能进行储存。

在电热元件的研究中，材料的形状与其工作温度和储热体功率有关，一般线材加工成螺旋形元件使用，而螺旋电热元件由于螺旋方向和电流流向不同影响其磁场分布；带材加工成波形元件使用，其波形也会影响磁场分布。实际工况中蓄热体内部环境复杂(潮湿、高温、电磁场交织等)，蓄热体、电热元件中均有金属材料分布。而在施加三相交流电运行中，螺旋电热元件由于电磁力引发的位移形变量如图1所示。

图1 电热丝形变量Fig.1 Electric heating wire shape variable

为了使固体电储热系统在800 ℃左右的高电压工况下安全运行，电热元件能够尽量避免因磁场作用而导致的电热元件受力超本身机械受力强度造成的变形、断裂、移位，影响固体蓄热的工作性能，因此对两种加热元件对比分析。对于本文提出的电热元件相关的磁场问题，现有研究甚少，查找文献发现一般求解三维的磁场问题，同行提出了有限差分法、边界元法、混合算法等[9-12]，以上算法并不能直观反映电热元件的磁场分布规律或者只是形式解，而且计算速度较慢对仿真机器配置要求过高。为了更加直观、具体的得出电热元件的数据和对比结果，本文根据电磁场基本原理，进行有限元数值分析求解[13-18]，得出了两种电热元件的磁场分布状态，运用仿真数据生成磁密图，对比得出在相同的工况下两种电热元件磁密的具体分布情况。

解决固体蓄热磁场耦合的方式有多种，如隔离磁场、施加控制电路等[19-24]。由于一般方法在800 ℃高温高电压下实施困难，根据电磁场理论通电导线的磁场分布与电流方向、导体形状的影响有关。故本文通过改变电热元件形状削弱磁场场强及耦合，来减小蓄热体内部及相邻导体间的磁场力，对比螺旋电热元件发现波形电热元件在高电压下磁密更小，可使电热元件磁场力明显降低，并且对不同工作电压、不同型号下的波浪电热元件进行了磁密深入对比分析，为高温高电压固体蓄热体安全运行及电热元件的适用提供技术支持。

1 导体磁场建模方法

通常高温高电压固体电储热系统是在蓄热块预留的电热元件孔内布置电热元件通电加热，将电能转换为热能存储。因此，需要对蓄热块、电热元件分别建模。

1.1 蓄热块磁场模型

本文运用一种高温固体蓄热简化模型，其中砖体采用单块蓄热量为1.71 kW·h的蓄热砖，蓄热时间8 h，蓄热体内部留有等距加热孔放置加热元件，具体蓄热体模型如图2所示。磁场计算时对场域进行以下诠释：

（1）蓄热体以及内部细节为轴对称且分布均匀；

（2）两种不同类型电热元件下蓄热体的空间分布上属于X、Y轴向对称；

（3）在砖体导磁率几乎与空气相同的基础上忽略蓄热砖对磁场的影响；

（4）在所有场量正弦变化的同时不考虑高次谐波影响。

图2 固体蓄热体模型Fig.2 Solid heat storage model

1.2 电热元件磁场数学模型

电热元件研究类型分为如下两种。

（1）螺旋形电热元件：采用相邻加热丝绕向相反的连接方式，使相邻的磁极间通过同样的电流，但电流的流向相反。其中，电热元件所选用的螺距为18 mm，其螺径为47 mm，丝长为855 mm，丝直径3 mm。模型如图3所示。

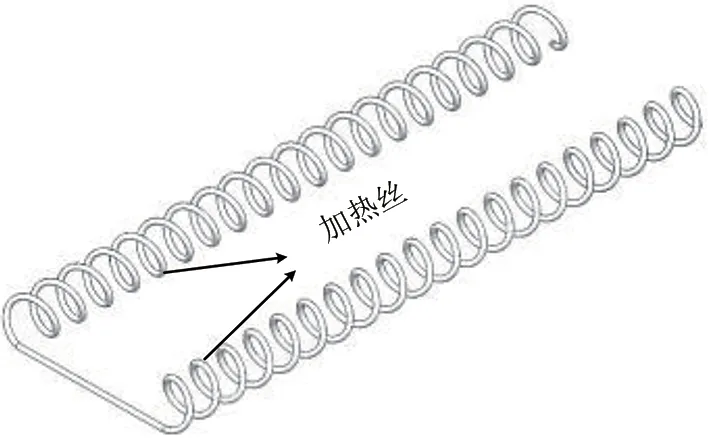
图3 螺旋加热丝模型Fig.3 Spiral heating wire model

（2）带材波浪形电热元件：采用U形弯处平角的处理方式，同样相邻的磁极间通以相同电流，电流的流向相反。其中，波浪直线部分长110 mm，厚度2 mm，宽度15 mm，波间距25 mm，模型如图4所示。

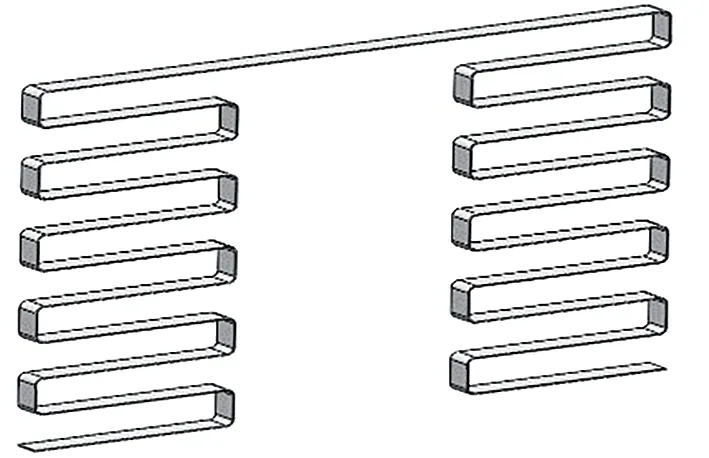
图4 波形加热丝模型Fig.4 Wave heating wire model

本文根据安培定律(即通电后电流使电热元件周围产生磁场，磁场再作用于通电电热元件)对以上两种模型导体间的磁力进行计算，再利用微分原理分解当作单位长度的通电导体间的磁力。计算公式如下

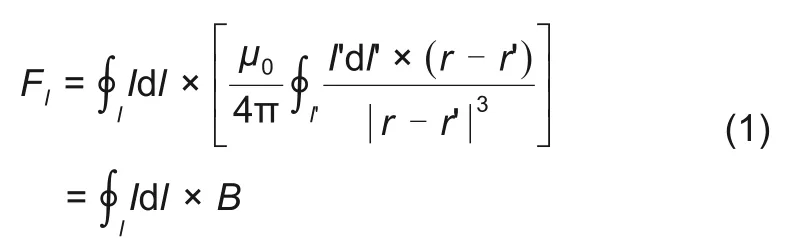
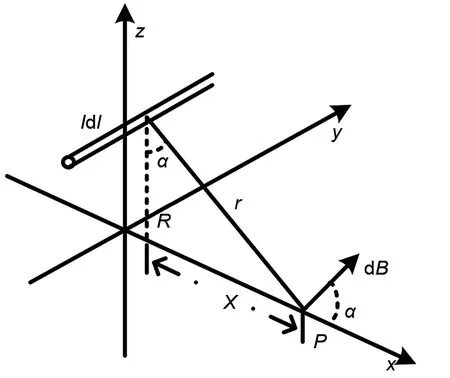
图5 电流元磁场计算示意图Fig.5 Schematic diagram of current element magnetic field calculation

对于垂直电流元的某磁场点P，设X = r'得到r'= r sinα，因此

根据每个电流元与点P的空间距离，得出

再利用先进多物理场仿真软件对其进行网格化后的有限元计算[25-27]。分别对两种电热元件通电后的磁场力在麦克斯韦方程组微分形式下求解，具体方程如下

（1）高斯定律

（2）高斯磁定律

（3）法拉第电磁感应定律

（4）安培定律

式中，D 为电位移矢量，C/m；ρe为电荷体密度，C/m3；E 为电场强度，V/m；H 为磁场强度，A/m；Je为电流密度，A/m2。

另外，由于蓄热装置中的蓄热块和空气的导电性能受温度影响较弱，其介电常数可视为定值，变化曲线如图6所示。

电热元件的介电常数受温度变化较大，电阻率和温度的关系如式(11)所示

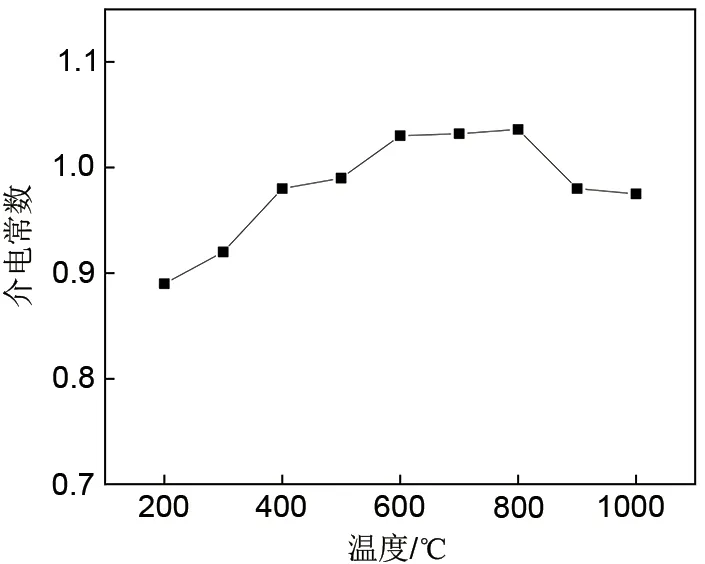
图6 钢渣蓄热材料介电常数-温度关系图Fig.6 Dielectric constant-temperature diagram of steel slag heat storage material

式中，M 为电阻率系数；T 为电热元件附近温度；K为常数。

并引入能够描述介质电磁特性的方程，更好表示电热元件在电磁场作用下的宏观特性，见式(12)

式中，Ɛ 为介电常数，F/m；Ɛr为相对介电常数；Ɛ0为真空介电常数(8.85×10-12F/m)。

式中，μ为磁导率，H/m；μr为相对磁导率；μ0为真空磁导率(4π×10-7H/m)。

2 仿真分析验证

本蓄热模型为对称结构，电热元件的排布也为对称性，砖体采用特制钢渣材质，其材料中钢渣含量大于50%，硅酸铝及黏土等矿物组分约20%，其他类天然矿物及氧化铝、氧化镁、氧化硅等原料共占约30%，混合不同粒度的原料制备的具有高热导率、高稳定性且致密不易变形的砖体，其主要物性指标如表1所示。

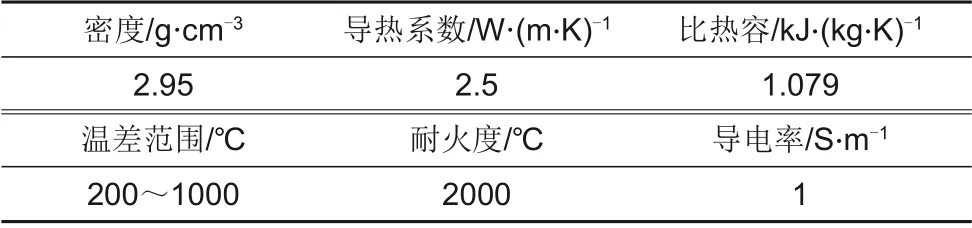
表1 蓄热块物理指标Table 1 Physical index of heat storage block

内部留有的加热丝孔放置由铁铬铝材料制成的电热元件(线材螺旋形、带材波浪形)。蓄热砖、空气的相对磁导率和相对介电常数均为1，电热元件的电阻率1.35 Ω∙m，相对介电常数1，相对磁导率2.58 H/m，电热元件密度7.25 g/cm3，最高使用温度为1000 ℃。具体如表2所示。

表2 材料物理特性参数Table 2 Material physical parameters

因蓄热体结构与加热丝排布均对称，加之整个高温固体蓄热体结构太大，在现有计算机的研究条件下，本仿真简化采用两个相邻加热丝孔研究，具有代表性即可[28-29]。固体蓄热装置外接110 kV三相线电压，电热元件采用ABC 三相电分接并联方式，通以180 A电流。两种方案仿真结果分别如下文所述。

当采用螺旋形电热元件(相邻绕向相反)时，加热丝的磁场分布如图7、图8所示。

图7 螺旋加热丝磁力线Fig.7 Spiral heating wire magnetic field line

图8 螺旋加热丝磁通密度Fig.8 Spiral heating wire magnetic flux density

根据上述两图分析，此种类型的电热元件磁场分布从电热元件内径中部位置开始到两端口磁密逐渐减弱，最大值为0.05866 T。磁力线穿过内径形成闭合回路，在螺径内分布较密，端口处开始分散且有相互交错现象，周围空间分布相对稀疏，且两电热元件磁力线分布呈对称状，但是螺旋电热元件自身内部磁场分布较乱，磁力线在电热元件附近向周围各个方向发散，轴向分布较密，加大了线圈的轴向力分布，自身容易受磁力作用形变，在高温下造成匝间短路。

当采用波浪形电热元件时，电热元件的磁场分布如图9、图10所示。

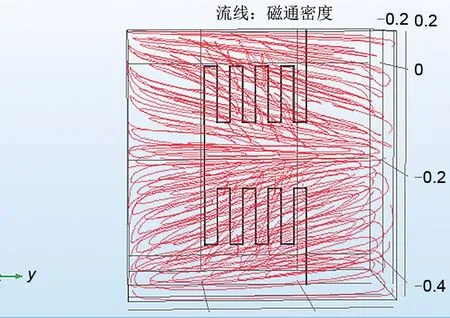
图9 波浪加热丝磁力线Fig.9 Wave heating wire magnetic field line

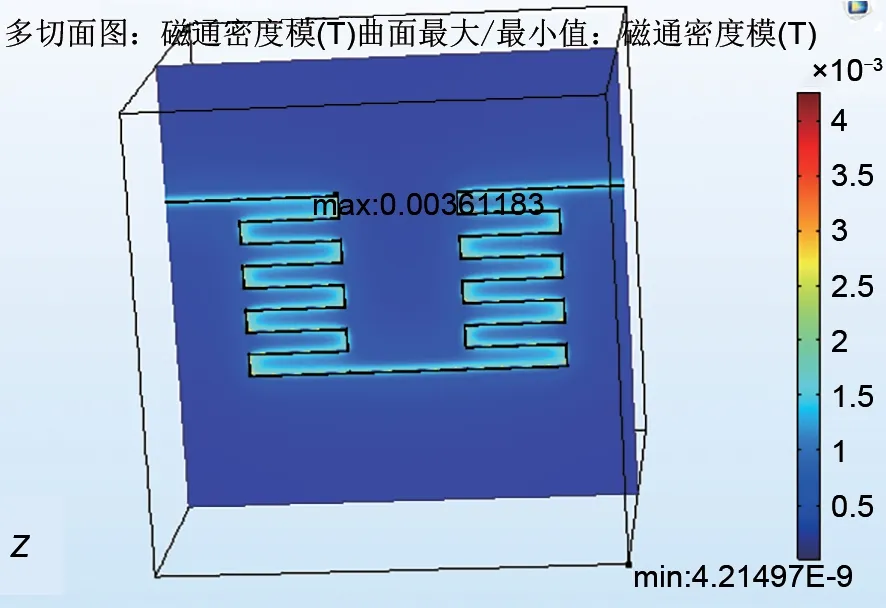
图10 波浪加热丝磁通密度Fig.10 Wave heating wire magnetic flux density

根据图9、图10分析，此种类型电热元件磁场分布较为均匀且规律，磁通密度在电热元件拐角处较密，其他均分布较弱，最大值为0.00361 T。磁力线分布与磁密分布相同，围绕整个电热元件形成轴向闭合回路，但整体磁力线密度相比螺旋形很弱。

两种电热元件横向磁通对比如图11、图12 所示。如图中所示，波浪加热丝横向磁密在电热元件截面处较强最大值为0.0004 T；螺旋加热丝横向磁密在螺旋线处最大，为0.065 T。波浪加热丝横向磁密相比螺旋形降低103个级别，降密优势明显。

两种加热丝轴向磁通对比如图13、图14 所示。如图中所示，波浪加热丝轴向磁密在电热元件截面处较强最大值为0.0012 T，其他位置磁密呈直线下降趋势；螺旋加热丝轴向磁密一直处于较强状态，在0.011～0.012 T 范围内呈水平线趋势。相比而言，波浪加热丝轴向磁密最大值小了10 倍，且其余部分磁密减弱明显。

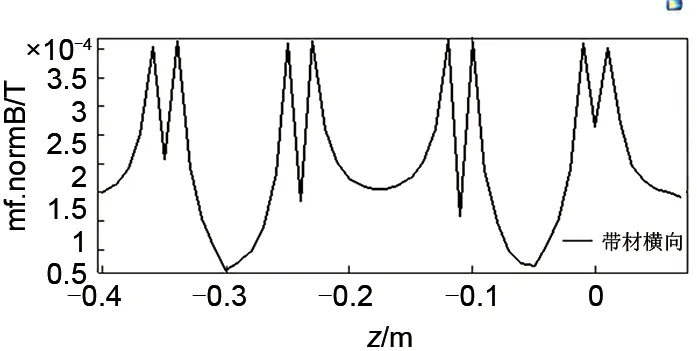
图11 波浪加热丝横向磁通密度Fig.11 Transverse magnetic flux density of wave heating wire

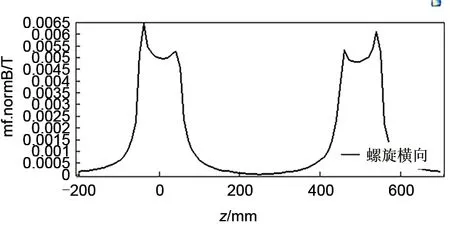
图12 螺旋加热丝横向磁通密度Fig.12 Transverse magnetic flux density of spiral heating wire

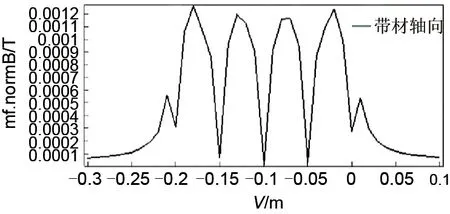
图13 波浪加热丝轴向磁通密度Fig.13 Axial magnetic flux density of wave heating wire

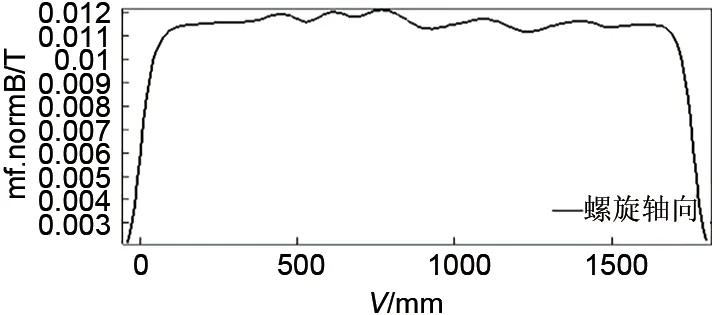
图14 螺旋加热丝轴向磁通密度Fig.14 Axial magnetic flux density of spiral heating wire

另通过本文提出的平角波形电热元件与规格相同U形弯处未做处理的波形电热元件电场强度对比如图15、图16所示。

图15、图16 表明在圆角电热元件与平角电热元件的对比中，两种电热元件的平直部分均电场分布均匀，强度为2.85×104V/m；但在折弯处出现电场强度内外差异较大情况，圆角内侧电场强度3.15×104V/m、外侧电场强度2.65×104V/m，在正常工况下折弯处极易发生元件自身内外侧击穿，发生事故影响蓄热安全；平角电热元件余留极短两弯折处(长度约4 mm)的电场强度内侧为3.15×104V/m、外侧为2.7×104V/m，此种处理大幅度缩短了内外侧差异部分长度，可避免自身击穿现象。

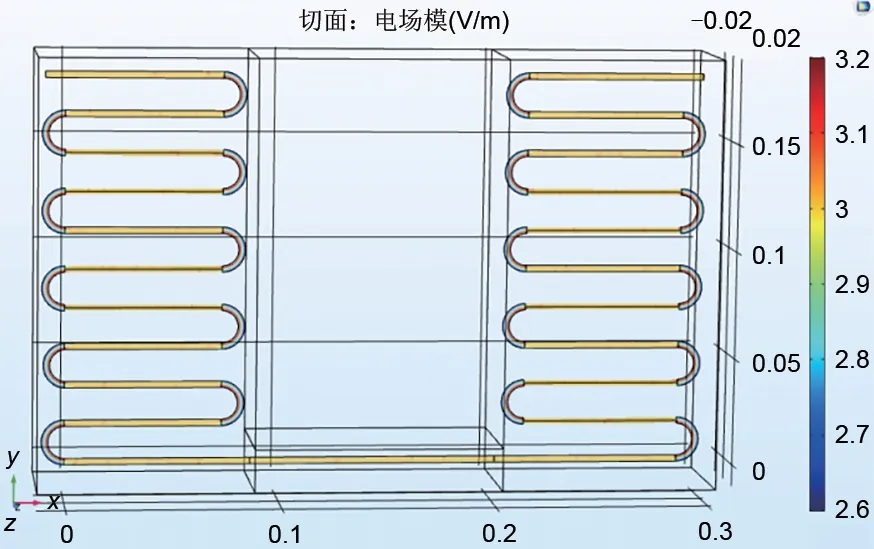
图15 圆角波形电热丝电场强度Fig.15 Electric field intensity of rounded wave heating wire

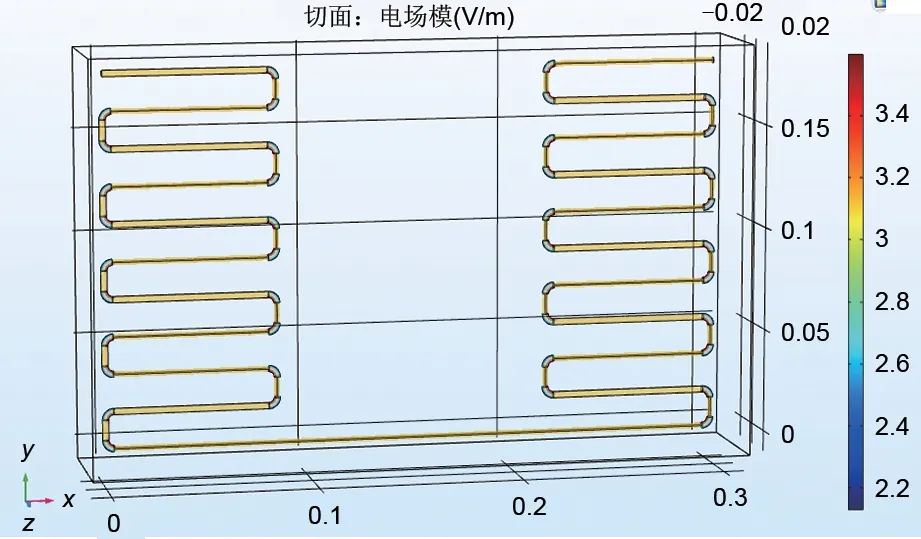
图16 平角波形电热丝电场强度Fig.16 Electric field intensity of flat-angle wave heating wire

根据上述两种加热丝磁场分析结果表明，带材波浪形加热解耦方案效果显著，很大程度上降低了固体蓄热内部导体周围的磁通密度。可见在800 ℃高温高电压的情况下，波浪电热元件电磁场分布及强度优于螺旋电热元件。同时平角电热元件可以有效避免因自身电场强度不同而导致的内外侧击穿。

此处为进一步分析不同电压对波浪加热丝电磁分布的影响，将分别在35、66、110 kV 电压下对波距25 mm 波形电热元件进行仿真分析，得出数据如图17、图18所示。

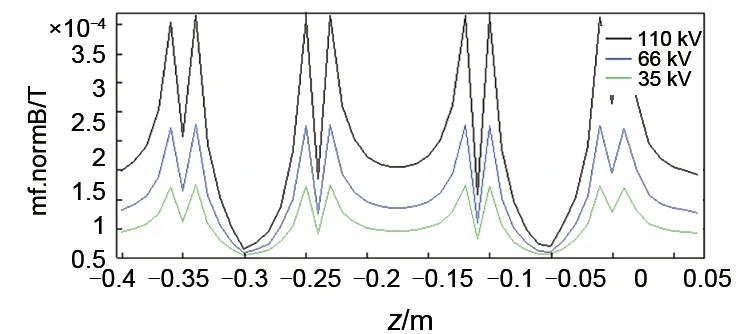
图17 不同电压下横向磁通密度曲线Fig.17 Transverse magnetic flux density curve under different voltages

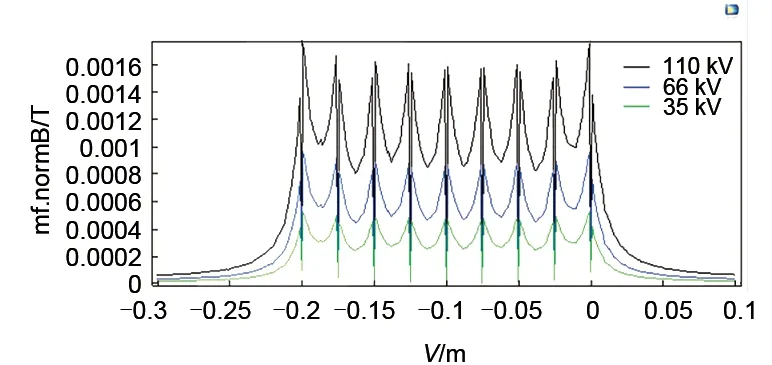
图18 不同电压下轴向磁通密度曲线Fig.18 Axial magnetic flux density curve under different voltages

上述电热元件电磁密度曲线对比表明，电热元件轴向、横向的磁密在不同电压级别下分布规律基本一致，均在电热元件表面附近磁密较高，远离电热元件位置呈现下降趋势，在两相邻电热元件的中间位置磁密最低。由于电压级别不同影响磁密数值大小及变化坡度，110 kV 电压下横向磁密最大0.0004 T、66 kV 电压横向磁密最大0.0002 T、35 kV 电压横向磁密最大0.0001 T，且电压越大磁密分布曲线越陡；轴向的磁密分布则相对规律，110 kV电压磁密在0.0009～0.0016 T之间、66 kV电压磁密在0.0004～0.0009 T之间、35 kV电压磁密在0.0003～0.0005 T 之间，且电压等级越低磁密差越小磁密分布越均匀。

为研究不同波距对磁密分布的影响，在对电热元件施加110 kV 电压其他规格保持不变情况下，分别对波间距为20、25、30 mm 其余参数不变的电热元件分析，得出数据如图19、图20所示。

图19、20 电热元件电磁密度曲线对比可知，在110 kV 电压下，不同波距电热元件的横向磁密分布曲线基本重合，波距30 mm 电热元件在某点数值上略微偏高，其对电热元件的影响可相对忽略不计；在轴向方面，磁密曲线由于波距的影响，曲线会随波距增大而变宽，电磁密度都在0.0008～0.0016 T 之间，较窄波距则会导致磁密分布集聚，加大磁密平均分布强度。

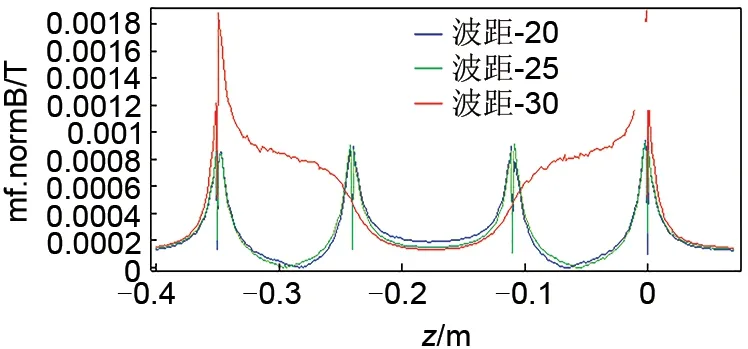
图19 不同波距横向磁通密度曲线Fig.19 Transverse magnetic flux density curve with different wave distance

图20 不同波距的轴向磁通密度曲线Fig.20 Axial magnetic flux density curve of different wave distance

表3 不同电压的磁密分布Table 3 Magnetic density distribution of different voltages

表4 不同波距的磁密分布Table 4 Magnetic density distribution of different wave pitch

综合分析上述数据，平角带材波浪型电热元件更合适在高温高电压(800 ℃、35 kV 以上)环境中使用。不同电压对同一型号电热元件磁密影响较弱，磁密分布规律一致仅数值上有略微不同，但窄波距会增大轴向磁通分布密度。随着施加电压的不同，可在高电压等级下增加波间距来降低轴向的磁密强度，从而减弱电热元件所受电磁力，使高温材料在机械强度降低时能够有效避免电热元件因磁场力超过材料承受强度而造成的形变、自身短路、击穿、连线跌落等现象。