基于简化型LSTM神经网络的时间序列预测方法

2021-05-26李文静王潇潇

北京工业大学学报 2021年5期

李文静，王潇潇

(1.北京工业大学信息学部，北京 100124； 2.计算智能与智能系统北京市重点实验室，北京 100124；3.智慧环保北京实验室，北京 100124； 4.北京人工智能研究院，北京 100124)

时间序列预测可以判断事物发展趋势，高效的预测模型可为应用决策提供有力依据[1]. 长短期记忆(long short-term memory, LSTM)神经网络对时间序列预测具有显著优势[2-4]，已广泛地应用于金融市场股票预测[5-7]、石油产量预测[8]、短时交通流预测[9]等领域，但标准LSTM神经网络用于时间序列预测具有耗时长、复杂度高等问题[10-11]. 围绕LSTM神经网络结构设计，目前已有大量学者进行了研究.

LSTM神经网络在训练过程中需要更新较多的参数，增加了训练时间[12]，故对其内部结构进行删减尤为重要. 一些研究者通过简化LSTM神经网络结构提出了多种基于标准LSTM神经网络的简化变体[13]，如去除遗忘门[14]、耦合输入门与遗忘门[15]、去除窥视孔连接[16]等. Greff等[13]对多种LSTM神经网络简化变体的效果进行了评价，实验证明耦合输入门与遗忘门、去除窥视孔连接的简化变体可以在不显著降低性能的情况下减少LSTM模型的参数数量和计算成本. Cho等[15]提出一种包括重置门与更新门2个门结构的门控循环单元(gated recurrent unit，GRU)，实验证明GRU可以达到与LSTM模型相当的效果，并且能够很大程度上提高训练效率. Zhou等[17]提出只有一个门结构的最小门控单元(minimal gated unit，MGU)，实验证明MGU具有与GRU相当的精度，但结构更简单，参数更少，训练速度更快. Oliver等[18]通过耦合输入门与遗忘门以简化LSTM模型，使用一个门结构同时控制遗忘和选择记忆，该神经网络与其他LSTM模型简化变体相比能够减少对历史数据的依赖性，降低网络的复杂度，在网络性能不变的情况下缩短训练时间[19]. 然而，以上介绍的LSTM简化模型，仍需要更新和存储较多的参数，导致网络计算冗余，训练时间较长.

针对以上问题，近几年一些学者提出精简门结构方程的方法，进一步减少训练过程中需要更新的参数，提高训练速度. Lu等[20]通过精简标准LSTM网络门结构方程减少参数更新，提出3个模型并将其与标准LSTM网络结构比较，实验证明该模型在较少参数的情况下可获得与标准LSTM模型相当的性能. Rahul等[21]通过减少重置门和更新门的参数，提出GRU的3种变体，并对其性能进行了评估. 结果表明，这些变体的性能与GRU模型相当，同时降低了计算开销. Joel等[22]介绍了MGU的3种模型变体，通过减少遗忘门动力方程中的参数数目，进一步简化了设计，这3种模型变体显示出与MGU模型相似的精度，同时使用较少的参数减少训练时间. 根据以上分析，在减少门结构数量的基础上精简门结构参数能够在保证网络性能的前提下减少网络的训练时间.

由于Oliver等[18]提出的LSTM简化神经网络具有较短训练时间、较少参数数量等优点，本文基于该网络提出简化型LSTM神经网络，在耦合门结构的基础上继续对门结构方程中的参数进行简化，可以更大程度上减少LSTM神经网络在训练过程中参数更新的数量，提高网络的训练速度. 通过2个基准数据集及污水处理过程出水生化需氧量(biochemical oxygen demand，BOD)质量浓度预测的实验验证，将其在3个时间序列数据集上与标准LSTM网络及其他变体进行比较评价，结果说明本文提出的简化型LSTM神经网络在训练时间减少的同时能够达到较好的时间序列预测精度.

1 标准LSTM神经网络结构

标准LSTM神经网络结构包含一个状态单元及3个门结构(输入门、遗忘门、输出门)，其中状态单元用于记录当前时刻的状态，各门结构用于控制信息的遗忘或记忆. 本文介绍的LSTM模型的结构是去除窥视孔连接的标准LSTM模型[16]，其内部结构图如图1所示. 标准LSTM模型的结构为

(1)

图1 LSTM神经网络内部结构详细示意图Fig.1 Detailed schematic diagram of the internal structure for LSTM neural network

式中：xt为当前时刻输入向量；ht为当前时刻输出向量；zt、it、ft、ct、ot、ht分别为输入信号、输入门、遗忘门、状态单元、输出门、输出信号；Wz、Wi、Wf、Wo分别为zt、it、ft、ot中的输入权重矩阵；Uz、Ui、Uf、Uo分别为zt、it、ft、ot中的递归权重矩阵；bz、bi、bf、bo分别为zt、it、ft、ot中的偏置矩阵；σ为sigmoid激活函数；g为tanh激活函数；⊙表示矩阵点乘操作.

对于只有一个重复隐含状态的递归神经网络(recurrent neural network, RNN)结构，若设定m为输入向量的维度，n为隐含层单元的个数，则每次迭代过程需要更新的参数个数为(mn+n2+n). 由于标准LSTM神经网络存在3个门结构(输入门it、遗忘门ft、输出门ot)与输入信号zt，由式(1)可知，标准LSTM神经网络在每次迭代过程中需要更新的参数个数为4(mn+n2+n).

2 简化型LSTM神经网络设计

本文提出的简化型LSTM神经网络，首先通过耦合输入门与遗忘门简化标准LSTM神经网络结构，其次对门结构方程中的参数进行精简以进一步减少网络参数，从而提高网络训练速度.

2.1 LSTM神经网络门结构简化设计

本文通过耦合输入门与遗忘门实现对标准LSTM神经网络的门结构简化，其结构由1个状态单元及2个门结构组成(如图2所示)，具体介绍如下.

图2 简化LSTM神经网络内部结构Fig.2 Internal structure of the simplified LSTM neural network

1) 输入门：控制需要输入到网络中的信息，该结构与标准LSTM神经网络相同，通过

zt=σ(Wzxt+Uzht-1+bz)

(2)

it=σ(Wixt+Uiht-1+bi)

(3)

实现.

2) 状态单元：状态单元ct结合输入信号zt与1-it控制的上一时刻的状态单元ct-1，其更新公式为

ct=(1-it)⊙ct-1+zt

(4)

由此可见，与标准LSTM神经网络不同，式(4)由1-it代替遗忘门ft对上一时刻的状态单元进行选择性记忆，当it数值为0时，上一时刻的单元状态全部记忆，当it数值为1时，上一时刻的单元状态全部遗忘，从而实现了输入门与遗忘门的耦合.

3) 输出门：控制当前时刻状态单元信息ct的输出程度，该结构与标准LSTM神经网络输出结构相同，通过

ot=σ(Woxt+Uoht-1+bo)

(5)

ht=ot⊙g(ct)

(6)

实现. 由此可见，输出门ot控制神经网络的最终输出. 若ot数值为0，则当前时刻单元状态ct全部不输出，ht输出值为0；若ot数值为1，则当前时刻单元状态ct全部输出.

经过输入门与遗忘门的耦合，LSTM网络在简化后由2个门结构组成，每次迭代过程需要更新的参数个数为3(mn+n2+n)，与标准LSTM神经网络结构相比减少了25%.

2.2 LSTM神经网络门结构参数精简方法

虽然耦合输入门及遗忘门简化了标准LSTM神经网络的结构，然而在每次训练过程中均需对输入权重矩阵Wz、Wi、Wo进行更新，由此导致计算量较大，训练时间较长. 针对该问题，本文通过简化门结构方程的参数进一步对LSTM神经网络结构进行精简，在不损失精度的前提下缩短网络的训练时间.

本文主要通过2种方法精简门结构方程，包括：1) 去除输入权重矩阵Wi、Wo；2) 去除输入权重矩阵Wi、Wo与偏置矩阵bi、bo. 本文将经过以上2种形式简化后的LSTM神经网络分别简称为LSTM- 简化型Ⅰ神经网络和LSTM- 简化型Ⅱ神经网络，以下分别对这2种简化型LSTM神经网络进行介绍.

1) LSTM- 简化型Ⅰ神经网络

该简化方法通过去除输入门与输出门中的输入权重矩阵Wi、Wo进一步简化LSTM神经网络，由

(7)

构成.

由此可见，与标准LSTM神经网络的门结构控制信号不同之处为：该网络门结构控制信号由t-1时刻输出信号ht-1、递归权重矩阵及偏置矩阵2项组成，在每次迭代过程中该网络需要更新的参数个数为3(mn+n2+n-2mn)，降低了计算复杂度.

2) LSTM- 简化型Ⅱ神经网络

该简化方法在去除输入门与输出门中输入权重矩阵Wi、Wo的同时，将偏置矩阵bi、bo去除，由

(8)

构成.

由此可见，与标准LSTM神经网络的门结构控制信号不同之处为：该网络门结构控制信号仅由t-1时刻输出信号ht-1、递归权重矩阵1项组成，在每次迭代过程中该模型需要更新的参数个数为3(mn+n2+n-2mn-2n)，进一步降低了LSTM神经网络的计算复杂度.

2.3 简化型LSTM神经网络学习算法

本文采用梯度下降算法[23-24]对提出的简化型LSTM神经网络的参数进行学习，定义损失函数计算公式为

(9)

式中：hd,t为网络在t时刻的期望输出；ht为网络在t时刻的实际输出.

下面以LSTM- 简化型Ⅰ神经网络为例，介绍参数更新过程.

步骤1根据

δht=δzt+1Uz+δit+1Ui+δot+1Uo

(10)

δzt=δht⊙ot⊙g′(ct)⊙it⊙z′t

(11)

δit=δht⊙ot⊙g′(ct)⊙zt⊙i′t

(12)

δot=δht⊙g(ct)⊙o′t

(13)

计算t时刻输出值ht及输入信号zt、it、ot的误差项. 其中, 导数形式展开公式为

g′(ct)=1-g(ct)2

(14)

z′t=zt(1-zt)

(15)

i′t=it(1-it)

(16)

o′t=ot(1-ot)

(17)

步骤2计算t时刻输入权重矩阵、递归权重矩阵、偏置矩阵的更新值公式为

δWz,t=δzt⊗xt

(18)

δUΩ,t=δΩt⊗ht-1

(19)

δbΩ,t=δΩt

(20)

式中：⊗为矩阵叉乘操作；Ω分别为{z,i,o}中的任意一个.

步骤3根据

Wz,t=Wz,t+1-η×δWz,t

(21)

UΩ,t=UΩ,t+1-η×δUΩ,t

(22)

bΩ,t=bΩ,t+1-η×δbΩ,t

(23)

计算t时刻更新后的输入权重矩阵、递归权重矩阵、偏置矩阵. 式中η为学习率.

步骤4计算训练样本的均方根误差(root mean squared error, RMSE)，如果训练样本的RMSE达到期望训练样本的RMSE或达到最大迭代次数，则参数更新结束，否则返回步骤1.

对于LSTM- 简化型Ⅱ神经网络，由于其门结构方程在LSTM- 简化型Ⅰ神经网络的基础上进一步去除了偏置矩阵，其权重矩阵更新与LSTM- 简化型Ⅰ神经网络相同，如式(21)(22)所示.

3 实验结果和分析

为了验证所提出的简化型LSTM神经网络在时间序列预测上的有效性，本文采用RMSE评价模型的预测准确性[25-27],公式为

(24)

式中N为样本个数. 将其与标准LSTM神经网络、只进行门结构简化的LSTM神经网络(简称LSTM- 变体Ⅰ)、仅去除输入权重矩阵的LSTM神经网络(简称LSTM- 变体Ⅱ)、仅去除输入权重矩阵与偏置矩阵的LSTM神经网络(简称LSTM- 变体Ⅲ)等多种LSTM模型的性能进行比较，在参数设置(包括LSTM模型状态单元维度、学习率、期望训练样本的RMSE、迭代次数)相同的情况下分别计算训练和测试RMSE、训练时间及所需更新参数个数等，所有实验独立运行20次并求取均值.

3.1 时间序列基准数据集

在本节中采用2个时间序列基准数据集(Lorenz时间序列、Mackey-Glass时间序列)评估简化型LSTM神经网络的性能.

3.1.1 Lorenz时间序列预测

Lorenz系统是一种大气对流数学模型[28]，它被广泛地用作时间序列预测的基准实验以评价模型的有效性. 其系统方程为

(25)

式中：x(t)、y(t)、z(t)为三维空间Lorenz系统的序列；a1、a2、a3为系统参数，a1=10，a2=28，a3=8/3.

图3 LSTM- 简化型Ⅰ对Lorenz时间序列预测的训练过程及测试效果Fig.3 Training process and testing results for the simplified LSTM Ⅰ in Lorenz time series

在本实验中，生成5 000组Lorenz样本,仅使用y维样本y(t)进行时间序列预测. 前2 000组作为训练样本，后3 000组作为测试样本. 以[y(t)y(t-1)y(t-2)]为输入向量，预测y(t+1)的值. 设定状态单元维度为8，学习率η为0.01，期望训练样本的RMSE为0.060 0，最大迭代次数为1 000次. 当训练样本的RMSE达到期望训练样本的RMSE或最大迭代次数时，停止参数更新.

LSTM- 简化型Ⅰ、Ⅱ的训练过程RMSE曲线分别如图3、4中的(a)所示. 从图中可以看出，本文提出的简化型LSTM神经网络的训练RMSE可以快速收敛. 其测试结果如图3、4中的(b)(c)所示，可以看出其均可以达到较好的拟合效果.

表1对比了不同模型的性能，可以看出，(LSTM- 变体Ⅰ)或(LSTM- 变体Ⅱ、Ⅲ)均可以减少更新参数个数并缩短训练时间，但LSTM- 变体Ⅰ、Ⅱ的训练时间短于LSTM- 变体Ⅲ，同时LSTM- 简化型Ⅰ在需要更新的参数个数比LSTM- 变体Ⅲ较多的情况下训练时间显著缩短，均说明门结构精简相对于简化门结构方程对简化LSTM神经网络的效果更显著. 通过实验结果分析可以得出，本文提出的LSTM- 简化型Ⅰ、Ⅱ神经网络能够在不显著降低预测精度的情况下，进一步缩短训练时间，减少LSTM神经网络的计算复杂度，减少预测时间，更易对时间序列信息预测.

3.1.2 Mackey-Glass时间序列预测

Mackey-Glass时间序列预测问题已被公认为评估网络性能的基准问题之一[29]. 时间序列预测由离散方程

(26)

产生. 式中:a=0.1,b=0.2,τ=17,x(0)=1.2.

在本实验中，选取样本1 000组，其中前500组作为训练样本,后500组作为测试样本. 以[x(t)x(t-6)x(t-12)x(t-18)]为输入向量，预测

图4 LSTM- 简化型Ⅱ对Lorenz时间序列预测的训练过程及测试效果Fig.4 Training process and testing results for the simplified LSTM Ⅱ in Lorenz time series

表1 Lorenz时间序列预测模型性能对比

图5 LSTM- 简化型Ⅰ对Mackey-Glass时间序列预测的训练过程及测试效果Fig.5 Training process and testing results for the simplified LSTMⅠ in Mackey-Glass time series

x(t+6)的值. 设定状态单元维度为10，学习率η为0.01，期望训练RMSE为0.006 0，最大迭代次数为700次. 当训练样本的RMSE达到期望训练样本的RMSE或最大迭代次数时，停止参数更新.

LSTM- 简化型Ⅰ、Ⅱ的训练过程分别如图5、6中的(a)所示. 从图中可以看出，训练RMSE可以达到期望训练RMSE. 测试结果、测试误差分别如图5、6中的(b)(c)所示，从图中可以看出，本文提出的简化型LSTM神经网络的测试结果可以达到较好的拟合效果.

从表2对不同模型进行比较的结果可以看出，3种LSTM变体(LSTM- 变体Ⅰ、Ⅱ、Ⅲ)通过对门结构精简或简化门结构方程的方式，均缩短了训练时间，并且LSTM- 变体Ⅰ在需要更新的参数个数比LSTM- 变体Ⅱ、Ⅲ较多的情况下训练时间缩短，同时LSTM- 简化型Ⅰ、LSTM- 变体Ⅲ均可以减少更新参数个数并缩短训练时间，但前者的训练时间短于后者，说明门结构精简相对于简化门结构方程对简化LSTM神经网络的效果更显著. 通过实验结果分析，可以得出，本文提出的LSTM- 简化型Ⅰ、Ⅱ神经网络在不显著降低预测精度的情况下进一步缩短训练时间，在时间序列预测过程中达到对时间序列信息简洁、快速预测的目的.

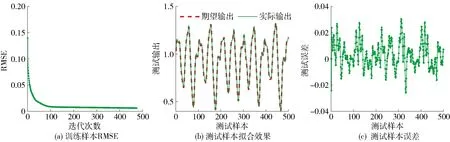
图6 LSTM- 简化型Ⅱ对Mackey-Glass时间序列预测的训练过程及测试效果Fig.6 Training process and testing results for the simplified LSTMⅡ in Mackey-Glass time series

表2 Mackey-Glass时间序列预测模型性能对比

3.2 污水处理中BOD预测

图7 LSTM- 简化型Ⅰ对BOD质量浓度预测的训练过程及测试效果Fig.7 Training process and testing results for the simplified LSTMⅠ in BOD mass concentration prediction

BOD是污水处理中评价水质的重要指标之一,具有高度的非线性、大时变的特征，很难及时准确地预测其质量浓度[30]. 本文利用LSTM- 简化型Ⅰ、Ⅱ神经网络对污水处理过程中的BOD进行建模，选取前8时刻的BOD质量浓度作为输入向量，下一时刻的BOD质量浓度作为输出变量.

选取北京市某污水厂的数据进行仿真，获得357组按照时间顺序进行排列的样本，选取前250组作为训练样本，后107组作为测试样本，将所有样本归一化至[-1,1]输入模型，并将样本反归一化后输出. 设定状态单元维度为15，学习率η为0.01，期望训练样本的RMSE为0.060 0，最大迭代次数为2 000次. 当训练样本的RMSE达到期望训练样本的RMSE或最大迭代次数时，停止参数更新.

LSTM- 简化型Ⅰ、Ⅱ的训练过程分别如图7、8中的(a)所示. 从图中可以看出，训练样本的RMSE能够达到期望训练样本的RMSE. 其测试结果反归一化后输出并计算测试误差，分别如图7、8中的(b)(c)所示. 从图中可以看出，简化型LSTM神经网络的测试结果均可以达到较好的拟合效果.

图8 LSTM- 简化型Ⅱ对BOD质量浓度预测的训练过程及测试效果Fig.8 Training process and testing results for the simplified LSTMⅡ in BOD mass concentration prediction

从表3的对比结果可以看出，在达到期望训练样本的RMSE、停止参数更新的情况下，LSTM- 变体Ⅰ比LSTM- 变体Ⅱ、Ⅲ需要更新较多的参数个数但需要较短的训练时间，同时LSTM- 简化型Ⅰ在需要更新的参数个数与LSTM- 变体Ⅲ相同的情况下训练时间显著缩短，均说明门结构精简对简化LSTM神经网络的效果更显著. 通过实验结果分析可以得出，本文提出的LSTM- 简化型Ⅰ、Ⅱ神经网络能够在精度相当的情况下进一步缩短训练时间，对BOD质量浓度快速预测.