基于骨架提取的拓扑优化最小尺寸精确控制
2021-05-25闫晓磊陈佳文张树忠黄晓东
闫晓磊,陈佳文,张树忠,张 勇,黄晓东
(1. 福建省汽车电子与电驱动重点实验室(福建工程学院),福建,福州 350118;2. 华侨大学机电及自动化学院,福建,厦门 361021;3. 澳大利亚斯威本科技大学科学、工程与技术学院,维多利亚,Hawthorn 3122)
经过近几十年的发展,拓扑优化已经广泛应用于航天航空、机械工程、海洋工程等领域[1-3]。但拓扑优化得到的结构几何形状往往比较复杂,常用的制造工艺难以加工或成本太高[4-5],因此,研究协同考量制造工艺约束的结构设计方法具有明显的工程实际意义。
在结构设计中,极限尺寸是一类重要的制造约束。比如构件的最小、最大尺寸以及孔洞的最小尺寸控制等。考虑尺寸约束是结构拓扑优化领域的一个难点,近年来,国内外学者在这方面做了一些工作。
Poulsen[6]引入非负函数MOLE,对特定方向上的密度梯度施加约束,实现了最小尺寸控制。Guest 等[7]以节点密度为设计变量,通过调节节点到单元的映射半径,实现拓扑结构的最小尺寸控制。类似地,白伟等[8]通过惩罚映射区域的单元平均密度,达到了控制结构最大尺寸的目的。Zhou 等[9]在三重密度场(设计密度、滤波密度、映射密度)框架下,通过联合调节滤波半径、映射阈值及其范围,提出了一种可调控最小尺寸的拓扑优化方法。采用类似的处理方法,Dunning[10]将其引入基于参数化隐式函数的拓扑优化方法,实现了最小尺寸控制。以上研究通过对设计变量施加约束,间接地隐式地实现了最小尺寸控制,但往往无法实现特征尺寸的精确控制[11]。
Zhang 等[12]基于SIMP(Solid Isotropic Material with Penalization)拓扑优化方法,借助于拓扑结构骨架实现了最大、最小尺寸的精确控制;Guo 等[13]基于水平集方法,利用符号距离水平集函数提取了拓扑结构的骨架,并通过约束其极值,实现了拓扑结构的最大、最小尺寸控制;Niu 等[14]基于MMC(Moving Morphable Components)方法,通过在组件的宽度上施加相同的上限和下限,实现了结构的等尺寸控制;Liu[15]基于水平集方法,通过对拓扑结构骨架的识别与分割,将拓扑结构分解为多个条状组件,实现了结构的动态极限尺寸控制。以上研究,借助拓扑结构的骨架,显式地实现了结构特征尺寸的精确控制,但这些方法难以考虑骨架变化对设计变量灵敏度的影响[16]。
渐进结构优化方法(Bi-directional Evolutionary Structural Optimization, BESO)是一种启发式的拓扑优化方法,具有原理简单、效率高、易实现的特点[17-18]。因此,本文尝试以BESO 方法为基础,通过细化边界单元及提取拓扑结构骨架,提出一种高效的拓扑优化方法,避免繁琐的公式推导的同时,实现最小尺寸的精确控制。
1 BESO 算法改进
BESO 拓扑优化方法,虽然具有效率高、原理简单的优点,但优化结果存在锯齿状边界问题[19],无法直接用于CAD 几何建模,也不利于特征尺寸的控制。对此,本文首先对传统BESO 方法进行改进。
1.1 拓扑优化模型
以最小化结构平均柔度为目标为例,拓扑优化模型可定义为:
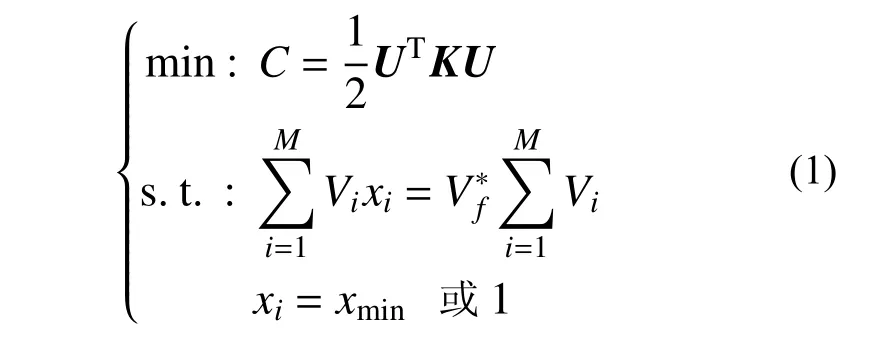
式中:xi为第i个单元的拓扑设计变量,当xi=1 表示该单元为实单元,当xi=xmin表示该单元为空单元(为避免求解困难,xmin通常取接近于零的小值,本文xmin取10-3);C为结构的平均柔度;U为节点位移向量;K为整体刚度矩阵;Vf*为目标体积分数;Vi为单元i的面积或体积;M为设计域单元总数。
1.2 灵敏度分析及单元滤波
在BESO 算法中,仍然采用SIMP 插值模型,即第i个单元的弹性模量可表示为:

式中:E0为基体材料的弹性模量;p为惩罚因子(本文取3)。
根据目标函数式(1),再结合插值模型式(2),可求得目标平均柔度C对拓扑设计变量xi的偏微分为:

有了灵敏度分析式(3),单元敏度数可以定义为:

为了抑制棋盘格模式和网格依赖性,同时将单元敏度数转化为节点敏度数,这里采用权重滤波方法[20]:

式中:rmin为过滤半径;rji为节点j和单元i中心的距离。
1.3 边界单元细化
为了得到光滑的边界,通常的做法是加密有限元网格,但网格增加势必会造成计算量的急剧增加。本文采用形函数插值方法,对结构拓扑边界上的单元进行虚拟细化,在不增加有限元网格的情况下,达到光滑结构拓扑边界的目的。下面给出具体细化过程。
首先,将结构边界上的某个单元划分为Ne个小单元(该小单元并不参与有限元计算),则第k个小单元的灵敏度可由该边界单元的节点灵敏度计算得到:

在优化过程中,并不是所有单元都进行上述细化处理,而仅细化结构拓扑边界上的单元。判断单元是否是边界单元,要根据节点灵敏度的大小排序确定,即边界单元的节点灵敏度满足:


2 拓扑结构骨架提取及最小尺寸控制
2.1 骨架提取算法
图形骨架具有中心性、同伦、单位性且不会改变原图形的拓扑特性。因此,采用骨架对尺寸精确定义以及控制具有明显优势。本文所采用拓扑细化算法[22]来提取拓扑结构骨架。
拓扑细化算法的核心就是逐层删去结构边界上的简单点(Simple point),所谓简单点就是删除之后不改变图形拓扑特征的点。在有限元框架下,若某边界实单元v满足下面的公式,则视该单元为简单点[23-24]:

式中:N3(v)为单元v的26 个邻域单元,即3×3×3基体,如图1 所示;δ 为变量的改变;G为该单元基体N3(v)的欧拉示性数;O为基体N3(v)的连接体数;S为实体单元。若第一式成立表示该单元满足欧拉特性;若第二式成立表示删除该边界单元后连通性不改变。
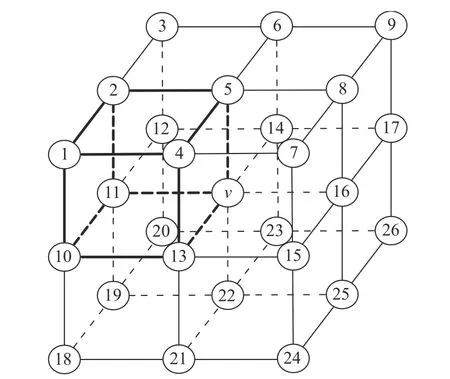
图 1 N2(v)和N3(v)基体Fig. 1 Frameworks for N2(v) and N3(v)
在实际操作中,第一步是选出设计域的边界,若N3(v)的26 邻域单元中只有一个实单元,则单元v为边界点中的端点,直接保留,继续第二步。
第二步验证欧拉特性。将3×3×3 基体N3(v)划分为8 个2×2×2 基体N2(v),则单元v的欧拉特性可计算为[25]:
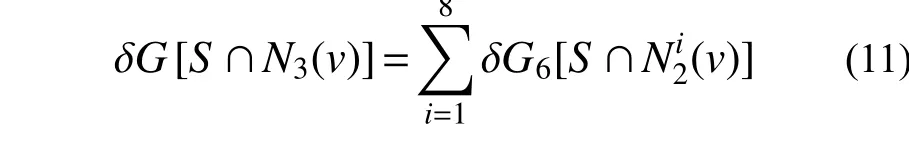
式中,G6为单元v的6 邻域欧拉特性,在第i个N2(v)基体中,单元v的6 邻域欧拉示性数的变化量可计算为:
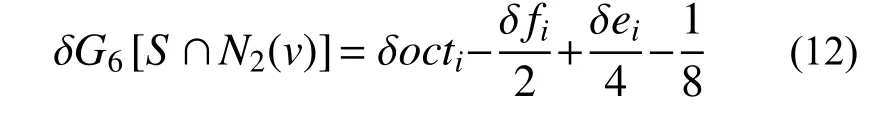
式中,ei、fi、octi分别为单元i所在N2(v)基体中实单元所形成的边、面和基体的数目。
第三步验证连通性。可采用八叉树算法[26],计算边界实单元v的连接体数,若计算得到的连接体数为1,同时边界单元v删除时式(11)为0,则该单元为简单点,直接删除,否则,保留。
2.2 骨架毛刺去除
利用第2.1 节过程,可提取到每一步优化后拓扑结构的骨架,但在拓扑结构边缘处的骨架可能会生成毛刺[27],使骨架形状失真。因此,在得到拓扑结构骨架后,还需要进行去毛刺处理。去除毛刺的原理比较简单,若骨架端点到连结点的长度小于阈值Lth,即认为该骨架分支为毛刺,进行删除。需要注意的是,在去除毛刺时,可能会将原连结点转变为新的端点,从而产生新的毛刺,因此,毛刺的去除须分级去除,直到无毛刺可去除。本文毛刺阈值Lth取10 个单元的长度。
2.3 最小尺寸控制
在迭代过程中,得到拓扑结构的骨架单元后,以最小控制尺寸dmin为直径,以骨架单元的形心为球心,扫掠整个骨架,即可确定最小尺寸对应的控制域B(dmin)。在优化过程中,始终保证形心在控制域B(dmin)内的单元全部为实单元,从而实现拓扑结构最小尺寸的精确控制。
此外,需要说明的是,拓扑优化过程中,拓扑构型的演化是通过空洞的生成与合并形成的,如果直接施加最小尺寸约束,可能会造成优化结果早熟[12],得不到最优解。为避免这一现象,本文采用逐渐强化约束的方法,即构造最小尺寸约束为:

3 拓扑优化最小尺寸控制算法步骤
根据上面分析,基于BESO 的最小尺寸控制拓扑优化算法可概括为以下步骤:
步骤1:设计域网格离散,初始化设计参数:收敛精度ε、目标体积分数Vf*、进化率ER、过滤半径rmin及最小尺寸dmin等;
步骤2:对结构进行有限元方法分析,根据式(3)分析目标函数的单元灵敏度;
步骤3:根据式(5)计算节点灵敏度;
步骤4:确定当前迭代步材料目标体积分数:

步骤5:节点灵敏度排序,细化边界单元;
步骤6:单元(包括小单元)删、添;
步骤7:提取拓扑结构的骨架;
步骤8:根据式(13),确定控制域B(dmin),施加最小尺寸约束;
步骤9:更新结构;
步骤10:返回步骤2,直到满足体积约束和目标函数收敛精度。
4 实例分析
下面通过实例来验证所提出的最小尺寸控制拓扑优化算法。为简化起见,以下所有实例中,材料的弹性模量和泊松比都分别取为E=1 GPa、ν=0.3;进化率ER=0.01;另外,二维单元细化规模为10×10 个小单元、三维单元细化规模为10×10×10 个小单元。
4.1 算例1. L 型梁结构
首先,为验证算法的有效性,对于如图2 所示L 型梁结构,右端中点受大小为1 kN 的集中载荷作用,上边界固支;初始设计域被离散为5120 个矩形有限元网格;过滤半径rmin=2 mm,最小控制尺寸为dmin=2 mm。
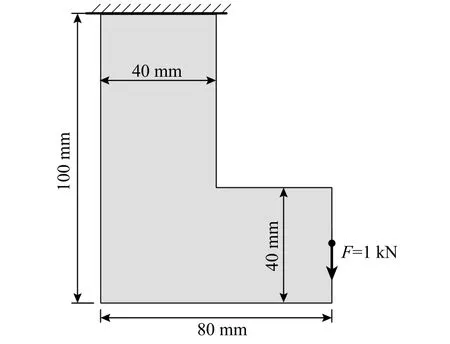
图 2 L 型梁结构设计域Fig. 2 Design domain of a L-shape beam
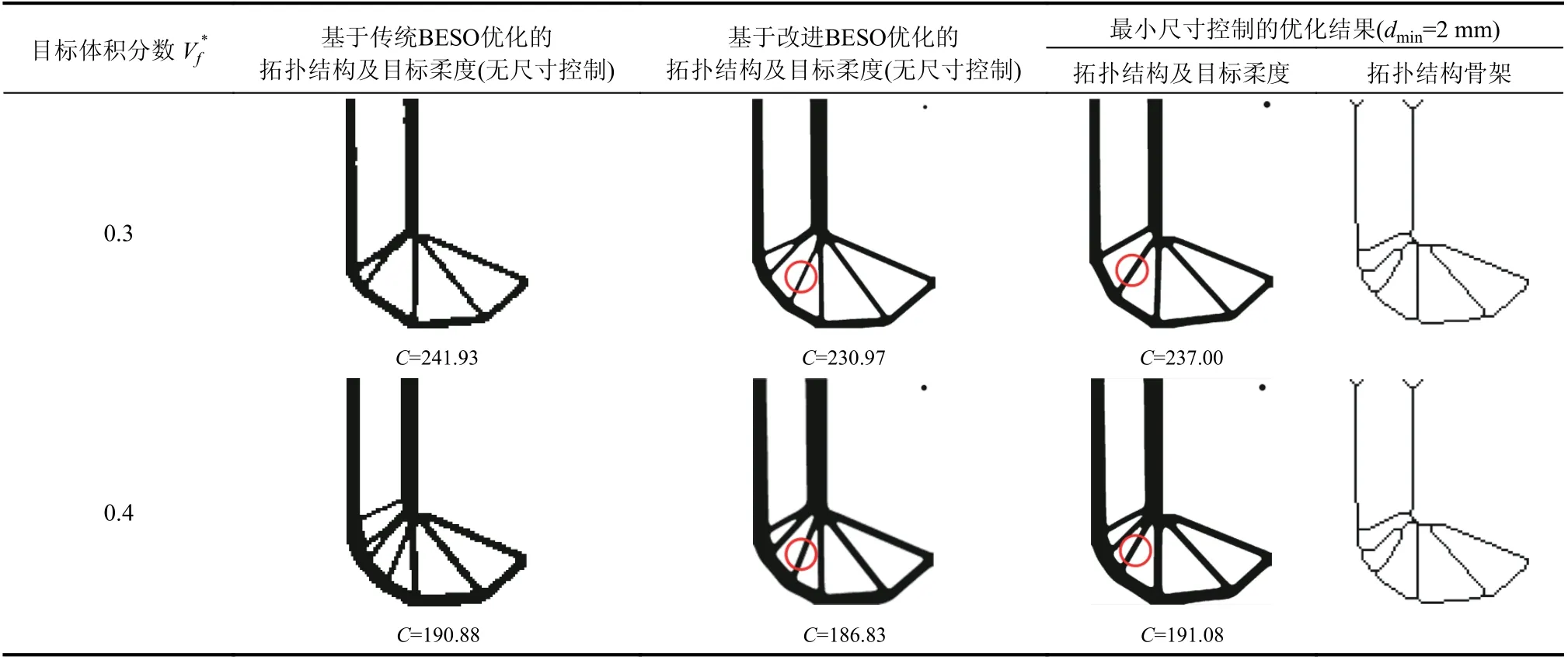
表 1 L 型梁不同体积分数下的最小尺寸控制优化结果Table 1 The optimized results with minimum length scale control under different volume fractions for the L-shape beam
图3 给出了表1 对应的最小尺寸约束下不同目标体积分数约束时的目标函数收敛曲线。优化过程体积分数逐渐减少到目标体积分数,目标柔度逐渐增大直至收敛,收敛过程十分平稳。
4.2 算例2. 悬臂梁结构
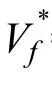
先来研究最小尺寸约束施加过程,即参数β 的影响,此时固定最小尺寸约束为dmin=2 mm。图5 对比了β=5、β=10、β=20 情况及无尺寸约束的优化结果。从图5 中可以看出,最小尺寸约束的施加对优化结果具有显著的影响。β 较小时,由于整个优化过程最小尺寸约束都在起作用,此时优化得到的拓扑结构中存在很多杆件,并且目标柔度变大(相对于无尺寸约束情况);随着β 的增加,最小尺寸约束相当于施加在优化过程的后期,此时拓扑结构中杆件逐渐变少,结构趋于简化,目标柔度也逐渐接近无尺寸约束情况。事实上,在拓扑构型演化中,空洞的生成与合并过程也就是最小尺寸“杆件”的产生与断裂过程,最小尺寸约束的施加势必会影响这一过程,造成优化过早收敛[10,12],而通过松弛施加最小尺寸约束可以有效避免这一问题。

图 3 最小尺寸控制下的目标柔度及体积分数迭代曲线 (dmin=2 mm)Fig. 3 Iterative history curves of the objective compliance and the volume fraction with the minimum length scale control (dmin=2 mm)
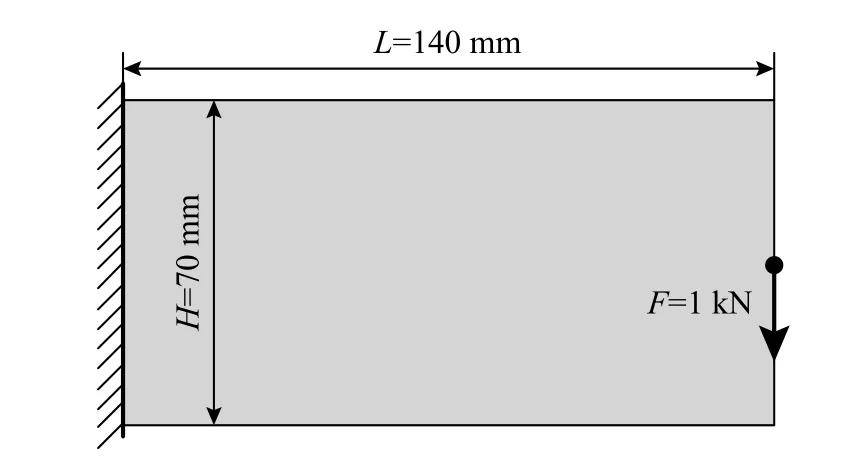
图 4 悬臂梁设计域Fig. 4 Design domain of the cantilever beam
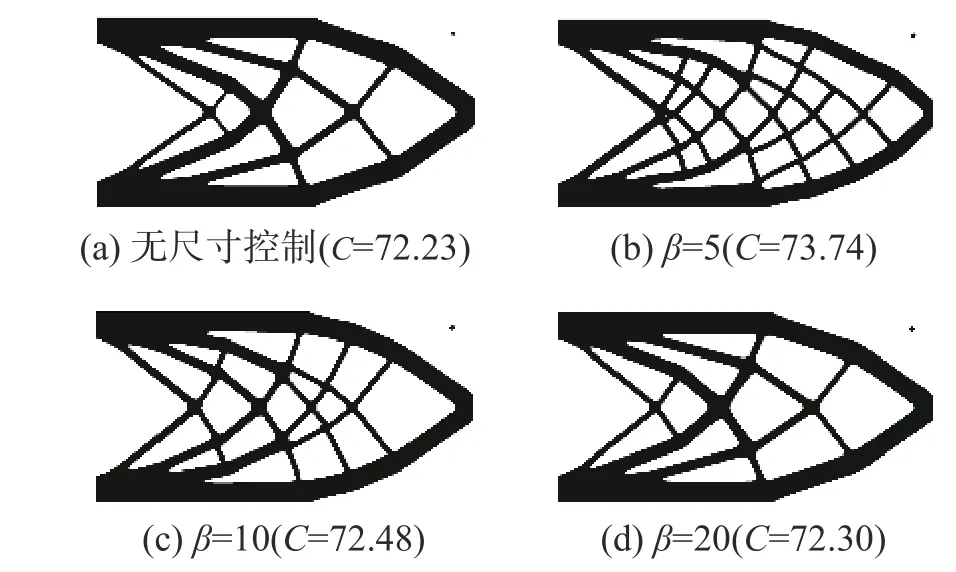
图 5 不同β 值的拓扑优化(dmin=2 mm)Fig. 5 Topology optimization results with different index β (dmin=2 mm)
下面研究最小控制尺寸dmin对结果的影响。图6 对比了最小尺寸分别为dmin=2 mm、dmin=2.5 mm、dmin=3 mm 及无尺寸约束情况下的拓扑优化结果,此时,β 设定为20。从图6 中可以看出,随着最小控制尺寸dmin的增大,结构中的最细杆件逐渐变粗,并且都满足了最小尺寸控制要求;但随dmin的增大,结构拓扑变得复杂,目标柔度也逐渐增大;可见,最小控制尺寸dmin的大小对优化结果具有显著的影响,设置最小控制尺寸可以避免细小支杆的产生,提高结构的稳定性,但过大的最小控制尺寸可能使设计结果性能变差且结构复杂。
4.3 算例3. 三维支座



图 6 不同最小尺寸约束的拓扑优化结果Fig. 6 Topology optimization results under different minimum length scale controls

图 7 三维支座设计域Fig. 7 Design domain of a 3D support
图8 对比了最终的拓扑优化结果,其中图8(a)为无尺寸控制的拓扑优化结果;图8(b)为施加了最小尺寸控制的拓扑优化结果;图8(c)为对应的拓扑骨架结构;对比图8(a)与图8(b),可以看到,支座中最细杆的尺寸可以被精确控制,但施加最小尺寸控制后,结构的整体刚度略有下降(目标柔度略有上升);图8(d)为体积分数及目标函数收敛曲线,从图中可以看出,施加最小尺寸控制后,迭代收敛过程依然很平稳。

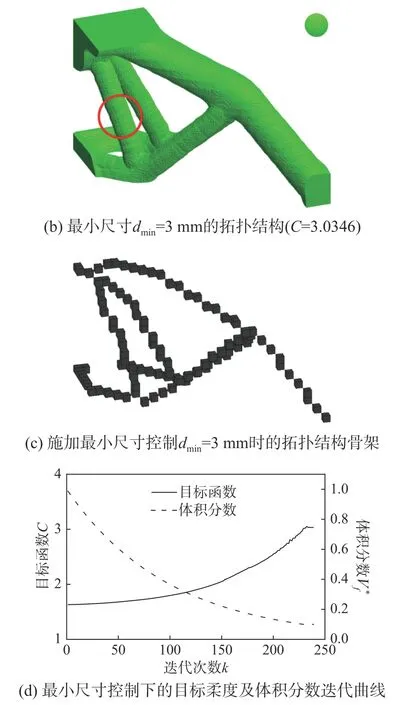
图 8 三维支座施加最小尺寸控制的拓扑优化结果Fig. 8 Optimized results with minimum length scale control for the 3D support
5 结论
本文在改进BESO 算法的基础上,通过提取拓扑结构的骨架,提出了一种可控制最小特征尺寸的拓扑优化方法。二维和三维算例表明:
(1) 该方法可以显式地实现结构最小尺寸精确控制;
(2) 合理地设置最小控制尺寸可以避免结构产生细小支杆,提高结构的稳定性,但过大的最小控制尺寸会使结构变得复杂且性能变差;
(3) 最小尺寸约束的施加对拓扑构型演化过程影响显著,本文通过最小尺寸约束松弛施加的方法,有效避免了优化过程早熟的问题。
在后面工作中,作者将进一步对拓扑结构孔洞尺寸及其他制造工艺约束的协同控制进行研究。
