隔震建筑橡胶柔性管道易损性模型研发及应用

解琳琳，闫海洋，曾德民，李爱群,3，杜志超，钟勃健

(1. 北京建筑大学土木与交通工程学院，北京 100044；2. 北京建筑大学工程结构与新材料北京高等学校工程研究中心，北京 100044；3. 东南大学土木工程学院，南京 210096；4. 北京建工建筑设计研究院，北京 100044)

隔震技术可显著提升上部结构的抗震性能和震后可恢复能力(即韧性)[1-4]，柔性管道作为隔震层中的关键元件，是保障隔震建筑功能(给水、排水、输气)的重要非结构构件[5-7]，隔震层的大变形特性对隔震层柔性管道提出了较大需求。目前，橡胶柔性管道由于其良好的变形特征和承载能力，逐渐得到工程界的认可与应用。与此同时，橡胶柔性管道的地震易损性模型及其损失后果函数研发对完善隔震建筑的地震韧性评价体系显得尤为重要。

部分学者对隔震层柔性管道进行了试验研究。尚庆学等[8]对5 个金属柔性管道进行了抗震性能试验，重点分析了不同密封构造和连接接头形式对其变形能力和破坏特征的影响规律。课题组分别开展了27 个金属柔性管道[9]和24 个橡胶柔性管道[10]的抗震性能试验，识别了柔性管道的关键损伤状态，明确了不同公称内径和设计长度等对其变形能力和破坏特征的影响规律。在柔性管道的易损性研究方面，尚庆学等[8]初步研究了金属柔性管道的易损性模型，但总的来说国内外对于柔性管道尤其是橡胶柔性管道的易损性研究还相对较少，对其不同损伤状态下的损失后果(修复时间和修复费用)函数的研究尚罕见报道。基于既有试验数据，建立橡胶柔性管道的地震易损性模型及其损失后果函数，明确不同方案下柔性管道的地震损伤概率，分析柔性管道对结构地震韧性水准的影响规律，可为全面保障隔震建筑的地震韧性能力提供重要支撑[11-12]。

针对上述需求，本研究基于课题组前期完成的24 个橡胶柔性管道抗震性能试验数据[10]，建立了橡胶柔性管道易损性模型和损失后果函数(下文所述“柔性管道”均指“橡胶柔性管道”)，并将其集成至我国《建筑抗震韧性评价标准》[13](下文简称为“评价标准”)评价软件中。为进一步明确不同柔性管道方案对结构地震韧性水准的影响，本研究设计了一5 层RC 框架隔震结构，以公称内径和设计长度为变量设置了6 种柔性管道方案，对该结构进行了设防地震和罕遇地震下的韧性评价，明确了柔性管道对该结构韧性水准的影响规律。本文的研究成果可为隔震建筑的地震韧性评价体系的完善提供重要参考。

1 易损性模型及损失后果函数

1.1 柔性管道易损性模型

课题组前期柔性管道试验[10]以行业标准《建筑隔震柔性管道》[14]为依据，考虑了2 种公称内径和4 种设计长度(共计8 组24 个试件)，对竖向安装的柔性管道进行了往复加载试验研究。本研究总结了柔性管道的损伤演化过程：加载位移较小时，试件本身存在冗余长度并不受力，当加载位移幅值达到某一限值时，管道绷直并开始受力，管内压强亦逐渐上升；当加载位移达到管道极限变形能力时，管道发生破坏导致漏水，管道丧失功能。课题组前期根据试验现象对柔性管道设置了2 个关键损伤状态：DS1“管道绷直”和DS2“管道破坏漏水”。当构件进入DS1 前，管道处于正常工作状态；进入DS1 未达DS2 前，管道会产生一定的拔出但不致破坏；进入DS2 后，橡胶破裂管道漏水，震后需立即更换。柔性管道试验中所有试件均经历了DS1，其中6 组18 个试件进入了DS2，其余2 组6 个试件采用了规范建议方案(DN50 设计长度750 mm、DN100 设计长度850 mm)均未发生破坏，具体破坏试件分组见表1，其中φi为同组试件破坏位移角均值(试件破坏时加载位移与设计长度比值)。

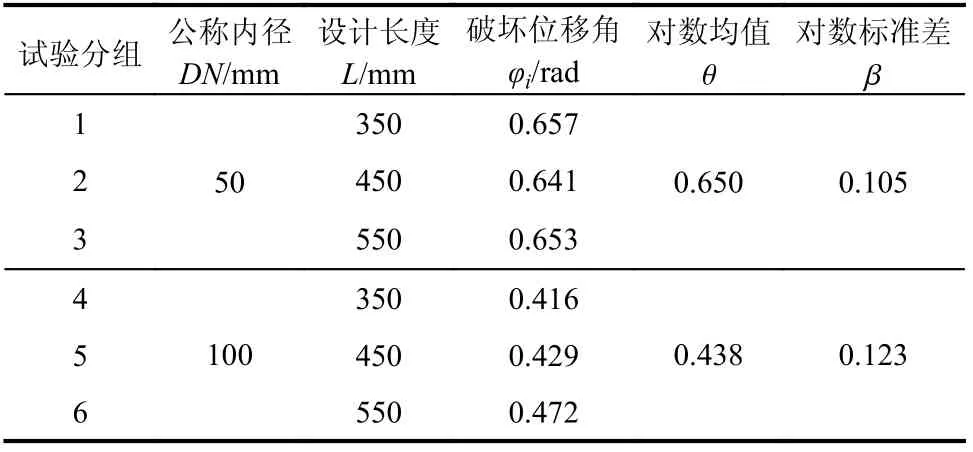
表 1 DS2 下柔性管道信息及易损性曲线参数Table 1 Information of the flexible pipes and parameters of fragility curve under DS2

基于上述管道试验研究成果，本研究将建立柔性管道易损性模型。目前普遍采用FEMA P-58 所推荐的分析方法来构建易损性函数[15-16]，即假定其满足对数正态分布，并可表示为：

式中：edp为工程需求参数，本文为位移角(隔震层位移与管道设计长度比值)；Φ(·)为标准正态分布累积函数；θ 和β 分别为某一损伤状态下工程需求参数的对数均值和标准差，可按式(2)和式(3)计算：

式中：M为所考虑试件的数目，本文区分不同公称内径的柔性管道易损性模型，对于2 种不同公称内径的试件均有9 个试件发生了破坏，因此M取为9；Zi为第i个试件发生损伤时的工程需求参数值；βu代表试件安装和试验加载条件等不确定性，当M＞5 时，βu取为0.1。

从表1 可以看出，对于具有相当公称内径的柔性管道，随着设计长度的增大其破坏位移角基本相当。在相同的设计长度下，随着柔性管道公称内径的增大，管道的破坏位移角显著降低，公称内径是影响管道破坏的关键因素。因此，在建立柔性管道易损性模型时需考虑不同公称内径，将不同设计长度的柔性管道破坏位移角均作为该公称内径管道的损伤数据，根据式(1)～式(3)计算获得2 种公称内径管道的易损性模型关键参数(如表1 所示)和易损性曲线(如图1 所示)。

图 1 DS2 下柔性管道易损性曲线Fig. 1 Fragility curve of flexible pipes under DS2

1.2 柔性管道损失后果函数

损失后果函数将损失的可能分布表示成损失状态函数的潜在关系，主要体现为修复与置换费用、修复时间、人员伤亡和其他影响[16]。其中修复费用需综合采购、运输以及技术人员劳务费等多因素进行考虑；修复时间应计入所有震损构件完成功能性恢复所需时间；人员伤亡依据建筑倒塌模态、构件损伤状态以及建筑居民数量进行确定。

柔性管道位于隔震层，发生破坏时可暂不考虑人员伤亡，因此其损失后果函数目前只考虑修复费用及时间。通过厂家调研确定包含了售价和运输费用的管道修复费用。课题组前期试验在开展上述8 组24 个试件时，对拆卸和安装时间进行了实测用于确定修复时间。柔性管道在未进入DS2 前，虽然管道会有一定程度拔出，但未发生破坏，因此可不进行修复或更换；当管道进入DS2 后，管道破坏发生漏水，需立即进行更换恢复其功能。具体损失后果函数如下：

1) 修复费用：柔性管道造价取决于公称内径与设计长度。本研究基于商家报价，综合考虑管道和端部连接接头总造价，确定公称内径50 mm和100 mm 的管道单位长度价格分别为1360 元和2460 元。

2) 修复时间：试验时考虑随机性的影响，通过任意两人合作的方式进行柔性管道的拆卸及更换，记录对应的修复工时，共24 个样本数据(同内径破坏与未破坏管道拆卸和安装时间基本相当)。目前国内外对于结构震后修复的准备时间的考虑方法尚不成熟，在确定各类构件修复时间时大都暂未考虑该因素影响，按修复/更换构件的时间建立相应的损失后果函数，本文在此也暂不考虑准备时间。同样假设修复时间函数曲线服从对数正态分布[17]，βu取为0.1 进行拟合。需要说明的是，同等公称内径不同设计长度柔性管道修复时间基本相当，而内径100 mm 相比于50 mm 的柔性管道法兰盘螺栓数量较多，拆卸-安装的工作量加大进而导致修复时间变长，因此以公称内径为变量对柔性管道修复时间曲线加以区分，如图2所示。公称内径为50 mm 和100 mm 时的柔性管道修复时间中位值分别为14.94 min (0.249 h)和31.62 min (0.527 h)，对数标准差β 分别为0.139 和0.149。

图 2 柔性管道修复时间后果函数Fig. 2 Consequence function for repair time of flexible pipes

2 分析案例设计

2.1 案例概况

本研究设计了一RC 框架结构，抗震设防烈度为8 度(0.20g)，场地类别为Ⅲ类，设计地震分组为第二组。结构共5 层，首层层高5.1 m，2 层～5 层层高为4.5 m，总高度为23.1 m，平面尺寸为109.2 m×76.8 m，三维模型如图3(a)所示。

基于《建筑抗震设计规范》(GB 50011-2010)[18]采用ETABS 软件进行隔震设计，所用隔震支座相关参数及支座布置分别如表2 和图3(b)所示，隔震层屈重比为1.48%，上部结构基本周期(X向)为0.772 s，隔震结构基本周期为3.269 s。为方便后续韧性评价，本研究在此根据评价标准相关要求选取8 条天然波和3 条人工波进行设计，其加速度反应谱与规范谱对比如图4 所示。从图中可以看出，在隔震前后周期点上加速度反应谱与规范谱误差不超过35%，平均误差不超过20%，符合规范要求[18]。结果表明，该结构隔震效果显著，减震系数平均值为0.18，大震隔震层位移平均值为321 mm，长期面压为8.43 MPa，罕遇地震下极大面压为12.15 MPa 且未出现拉应力，各项指标均满足规范相关要求[18]。

图 3 案例三维图及隔震层布置图Fig. 3 Three dimension view of the case and layout of the isolators

表 2 隔震支座参数Table 2 Parameters of the isolators

图 4 反应谱与设计谱对比Fig. 4 Comparison of response spectrum and design spectrum

2.2 案例结构响应

基于ETABS 软件建立精细有限元模型，上部结构采用弹性模型，隔震层为弹塑性模型，隔震支座采用Rubber Isolator 和Gap 单元模拟，梁柱采用Frame 单元模拟[19-21]。将上述11 条地震动沿结构主轴方向输入进行动力弹塑性分析，获取结构的地震响应，以设防地震及罕遇地震下的结构层间位移角及楼面绝对加速度为代表的典型结果如图5 和图6 所示，其中0 层代表隔震层，根据11 条地震动下隔震层位移均值与管道设计长度比值计算隔震层位移角(具体见表3)。

1) 在设防地震作用下，最大层间位移角0.09%(平均值为0.07%)出现在结构二层；最大楼面加速度0.83 m/s2(平均值为0.62 m/s2)出现在结构顶层。结构响应得到有效控制，结构构件和非结构构件基本处于无损状态。

图 5 设防地震作用下典型结构响应Fig. 5 Typical structural responses under design earthquake

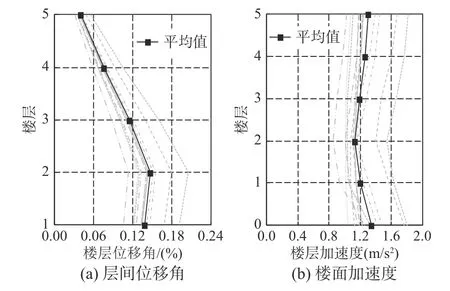
图 6 罕遇地震作用下典型结构响应Fig. 6 Typical structural responses under maximum considered earthquake

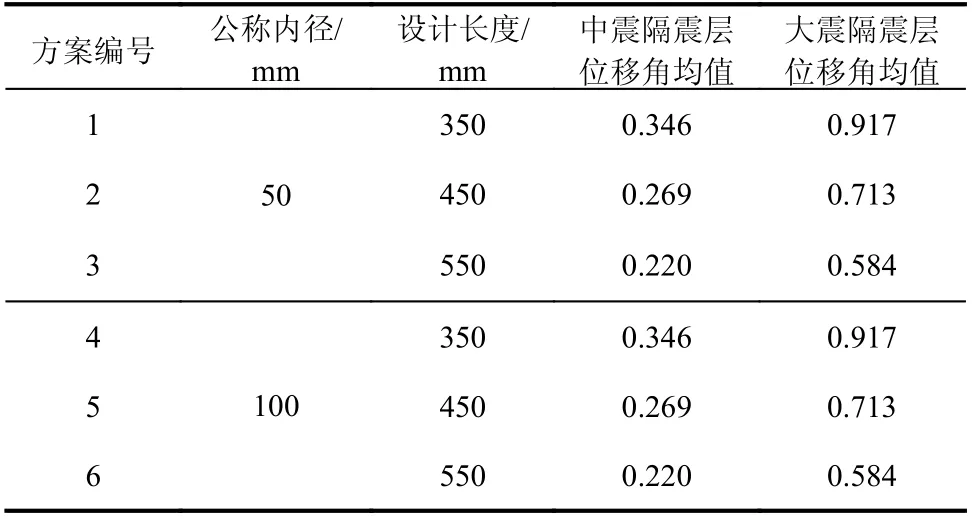
表 3 柔性管道参数及隔震层位移角均值Table 3 Parameters of flexible pipelines and mean drift ratios of seismic isolation layer

2) 在罕遇地震作用下，最大层间位移角仍出现在结构二层，最大值为0.21%，均值为0.15%，从图6(a)可以看出仅在一条地震动下最大层间位移角超过了1/550，上部结构基本处于弹性状态。最大楼面绝对加速度出现在结构顶层，最大值为1.82 m/s2，平均值为1.30 m/s2，整体控制良好。

3 考虑柔性管道的韧性评价

本研究将上文所提出的柔性管道易损性模型和损失后果函数集成至我国评价标准软件中，考虑柔性管道，对上述RC 框架隔震结构进行韧性评价。目前工程应用时，绝大部分隔震建筑所采用的柔性管道公称内径与设计长度基本相同。本研究参照已有工程，将隔震层柔性管道数量设置为62 根，考虑2 种不同公称内径(50 mm、100 mm)和3 种不同设计长度(350 mm、450 mm、550 mm)，共六种方案，研究不同柔性管道方案对建筑韧性水准的影响规律。

各方案集成韧性评价模型时，各案例间仅柔性管道不同，其余部分保持一致，重置费用约为3707 万元。结构构件和非结构构件分布信息见表4。按照评价标准相关规定，本研究采用的韧性评价指标：修复费用、修复时间及人员损失。其中修复费用指标为建筑修复费用与重置费用的比值；修复时间指标即震损构件恢复其功能所需修复时间；人员损失指标分别为伤、亡人数占全部人数的比例。3 项指标均采用蒙特卡洛模拟1000 次计算得到的具有84%保证率的拟合值确定，根据表5对三项指标等级进行评级，取最低等级作为该建筑抗震韧性等级。本研究在此考虑6 种柔性管道方案，对设防地震和罕遇地震作用下的建筑进行韧性评价。

表 4 使用的构件易损性类别Table 4 Fragility specification of components

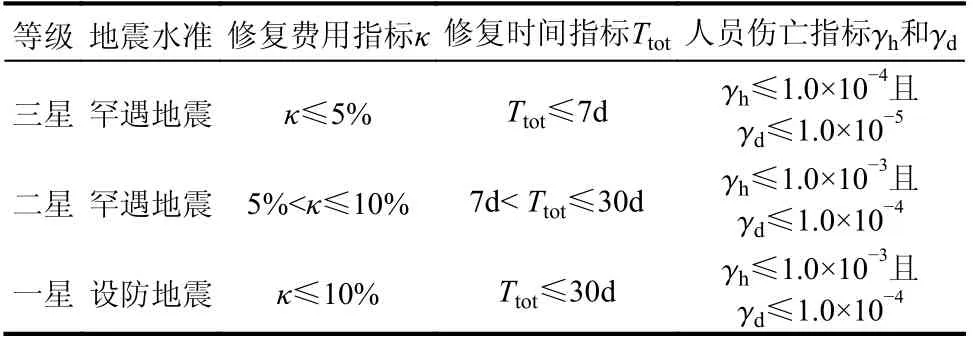
表 5 建筑抗震韧性等级评价Table 5 Seismic resilience assessment of buildings

3.1 修复费用

在设防地震和罕遇地震作用下，各方案的损伤构件修复费用见表6 和表7。

在设防地震作用下，从表6 可以看出：1) 上部结构隔墙饰面产生了一定程度的损伤，震后修复需花费0.66 万元；2) DN50 的管道在3 种设计长度下均未破坏，震后无需修复；3) 随着管道公称内径的增大，管道破坏风险增大，DN100 的管道在3 种设计长度下均有一定概率发生破坏，当设计长度最小时，从概率角度进入DS2 的管道数达33 根，震后修复费用达到了5.08 万元，约为隔墙饰面修复费用的7.5 倍，占总修复费用的88.5%，随着管道长度的增大，由于管道变形能力增大导致破坏概率显著降低，修复费用降低至0.71 万元；4) 设防地震作用下各方案建筑修复成本最高为5.74 万元，重置成本为3707 万元，修复费用指标为0.15%，可进行罕遇地震下评估确定结构韧性水准。

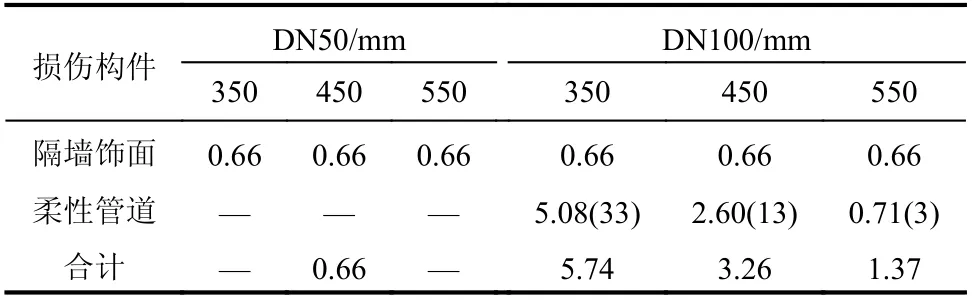
表 6 设防地震作用下修复费用 /万元Table 6 Repair cost under design earthquake

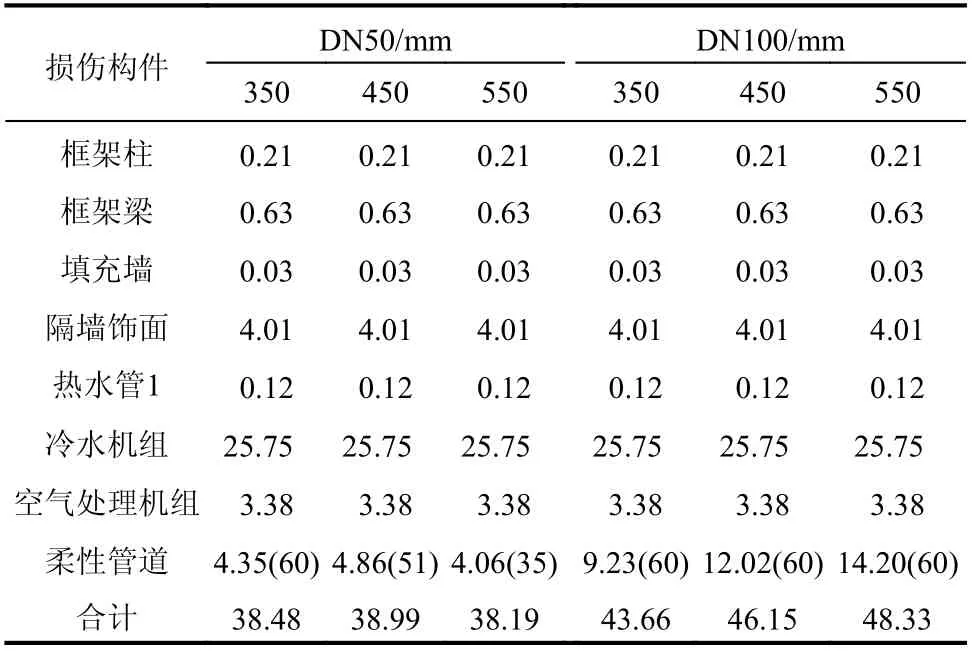
表 7 罕遇地震作用下修复费用 /万元Table 7 Repair cost under maximum considered earthquake

在罕遇地震作用下，从表7 可以看出：1) 由于楼面绝对加速度达到了1.82 m/s2，而冷水机组与空气处理机组DS3 所对应的损伤阈值中位值分别为0.2g和0.25g[13]，两者有一定概率损伤且修复费用达到了29.13 万元，占总修复费用的60.3%～76.3%，对修复费用评级起到了控制作用；2) 对于结构构件，由于结构层间位移角基本小于弹性限值，因此导致的修复费用相对较小，梁柱总修复费用为0.84 万元；3) 对于位移敏感型非结构构件(填充墙和隔墙饰面)，两者总修复费用达到了4.04 万元。

对于柔性管道：1) 由于大公称内径管道变形能力较弱，损坏数量较多且价格偏高，因此DN100方案组柔性管道修复费用整体高于DN50 方案组；2) 对于50 mm 内径管道，加大管道设计长度提高了变形能力，可使柔性管道损失数量减少，但管道造价却在提高，因此管道修复费用并没有得到明显控制；3) 对于100 mm 内径管道，罕遇地震作用下隔震层位移为321 mm，对应各方案的位移角分别为0.917、0.713 和0.584，而DN100 破坏位移角中位值为0.438，震后基本难以避免破坏，因此各方案柔性管道接近于全部破坏(数量达60 根)，此时管道设计长度决定了修复费用，当设计长度最大时，震后修复费用达到了14.20 万元，占总修复费用的29.4%。总的来说，罕遇地震作用下各方案建筑修复成本最高为48.33 万元，重置成本为3707 万元，修复费用指标为1.3%，评级为三星。

综上所述，柔性管道对隔震结构的震后修复费用存在一定程度的影响，在设防地震下较为明显，罕遇地震下虽不起控制作用，但也值得关注。虽然加大管道设计长度可降低破坏概率，但应采用规范建议的长度才能确保管道的地震安全。

3.2 修复时间

根据评价标准相关规定，在确定隔墙饰面及其他构件修复时间时，首先应明确构件在对应损伤状态下的单人修复工时，然后计算所需工人数量进而转化为修复时间；柔性管道的修复时间依据本文所提出的修复时间后果函数进行计算。设防地震和罕遇地震作用下同内径各方案柔性管道修复时间基本一致，不区分设计长度给出损伤构件修复时间，具体见表8。

表 8 各方案下修复时间 /dTable 8 Repair time of different schemes

在设防地震作用下，从表8 可以看出：1) DN50各方案柔性管道震后无损伤未引起修复工时；2) DN100 各方案柔性管道损坏数量虽各不相同，但由于修复工作可以同时展开，各方案柔性管道修复时间均一致(0.02 d)，为隔墙饰面修复时间的1/2；3) 建筑修复时间最高为0.06 d，整体水准高。

在罕遇地震作用下，从表8 可以看出：1) DN50和DN100 各方案柔性管道修复时间分别为0.02 d和0.05 d，由于大公称内径管道拆卸-安装工作量偏大，因此修复时间较长；2) 柔性管道损坏引起的修复工时占总修复时间仅0.01%，与其他受损构件相比，对修复时间评级并不起控制作用；3) 建筑修复时间最高为4.13 d，评级为三星。

综上所述，相比于修复费用，柔性管道对隔震结构的震后修复时间影响相对较小，整体未超过0.05 d，并不会影响相应韧性星级评定。

4 结论

隔震建筑的韧性评价需考虑隔震层柔性管道，然而现有研究对柔性管道的易损性模型及其损失后果函数研究还相对较少。针对橡胶柔性管道，本研究基于课题组前期开展的试验数据，明确了关键损伤状态，建立了易损性模型及损失后果函数。设计了一典型RC 框架隔震结构，考虑公称内径和设计长度影响设定了6 种管道方案，进行了设防地震和罕遇地震作用下的结构地震韧性评价，分析了不同柔性管道方案对建筑韧性水准的影响规律。得到的主要结论如下：

(1)确定了柔性管道2 个关键损伤状态：DS1“管道绷直”和DS2“管道破坏漏水”。采用FEMA 推荐的分析方法，以位移角(隔震层水平位移除以管道设计长度)为工程需求参数，区分公称内径为50 mm 和100 mm 的橡胶柔性管道，建立了两者DS2 状态的易损性模型，相应的中位值分别为0.650 和0.438，对数标准差分别为0.105和0.123。

(2)柔性管道经历DS2 之后须立即更换，本研究建立了修复费用和修复时间的损失后果函数。修复费用考虑了管道造价及运输费用，确定内径50 mm 和100 mm 的管道单位长度价格分别为1360 元和2460 元；基于试验时记录的24 个试件拆卸-安装数据，建立了修复时间函数曲线，内径50 mm 和100 mm 的柔性管道修复时间中位值分别为14.94 min (0.249 h)和31.62 min (0.527 h)，对数标准差分别为0.139 和0.149。

(3)本研究的隔震结构案例韧性分析结果表明，在设防地震作用下，小公称内径的柔性管道破坏概率小，各方案下震后均不需修复，大公称内径的管道则有一定概率破坏，当管道长度最短时其修复费用占比最大，达88.5%，但相应的修复工时短，仅需0.02 d。

(4)在罕遇地震作用下，尽管柔性管道的修复费用对韧性评级并未产生影响，但大公称内径柔性管道震后修复费用仍达到了29.4%。值得注意的是在不满足规范设计长度时，增大设计长度由于不能避免管道在大变形下破损，其修复费用反而随之增大，采用《建筑隔震柔性管道》[14]所规定的设计长度是控制该损失的有效方法。柔性管道损坏所引起的修复工时最高为0.05 d，仅占总修复时长的0.01%。