考虑锁相环多单相光伏逆变器并联稳定性分析

2021-05-25张自强高建勇时翔钟诚

电气传动 2021年10期

张自强，高建勇，时翔，钟诚

（1.国网甘肃省电力公司，甘肃兰州 730070；2.国网青岛供电公司，山东青岛 266002；3.东北电力大学电气工程学院，吉林吉林 132012）

近年来，电网中接入光伏逆变器不断增多，其并网控制稳定性得到学者广泛关注。光伏逆变器在设计初期未考虑电网阻抗，当其接入弱电网时，受电网阻抗交互影响，其稳定裕度下降，进而出现低频振荡、谐振等失稳现象[1-3]。

最新研究表明，单台逆变器接入电网失稳条件苛刻，逆变器失稳振荡现象通常发生在多台逆变器并网场景[4-9]。诺顿等效方法能有效地简化建模难度，具有良好的可扩展性，是多逆变器并网控制稳定性的重要方法[6-9]。文献[6]建立滞环控制并网逆变器诺顿等效阻抗，将多逆变器谐振现象分成内部谐振、并联谐振和串联谐振。文献[7-8]采用诺顿等效对多逆变器并网系统进行稳定性控制，指出多逆变器系统存在阻抗倍增效应。文献[9]基于诺顿等效，分析多光伏并网系统中的集电线路阻抗对稳定性的影响。

诺顿等效方法假定锁相环动态特性足够慢，忽略锁相环影响。但是，锁相环对逆变器低频段稳定性具有重要影响[10-12]，诺顿等效方法存在一定不足。

为此，本文以多台单相光伏逆变器并联接入电网为对象，建立含二阶广义积分锁相环（second order generalized integral-phase locked loop，SOGIPLL）的光伏并网逆变器等效导纳模型；与现有诺顿等效阻抗方法进行分析对比；分析锁相环带宽、参考电流大小对多逆变器并网系统稳定性的影响；最后，基于RT-LAB平台，搭建单相多逆变器并网实时仿真模型，验证理论分析的正确性。

1 系统描述

图1为典型多台单相光伏逆变器接入电网系统框图。

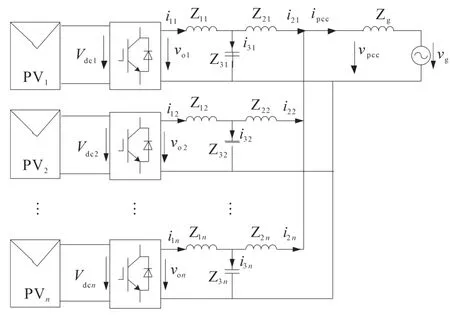
图1 典型n台光伏单相逆变器并网系统框图Fig.1 The block diagram of typical n-multiple single-phase PV inverters connected to power grid

图1中，外部电网采用理想电压源vg和等效阻抗Zg表示；n台逆变器并联接入PCC节点；Vpcc为PCC节点电压；ipcc为PCC节点电流；光伏逆变器采用 LCL 滤波器，分别用 Z1j，Z2j，Z3j表示，下标 j表示逆变器台号；i1j，i2j，i3j分别为第 j台逆变器流过Z1j，Z2j，Z3j的电流；Vdcj为 j台逆变器直流侧电压。

对于单相并网逆变器，静止坐标系下的比例谐振控制是目前通用控制策略[13]，其框图如图2所示。

图2 单相并网逆变器框图Fig.2 Block diagram of single-phase gird-connected inverter

图2中，Gcj为电流控制器；Gpllj为锁相环函数；Gpwmj为PWM函数；iref为参考电流；Iref为参考电流幅值。

Gcj控制器传递函数为

式中：kpj，krj分别为PR控制器的比例系数和积分系数。

Gpwmj通常取 1.5Ts一阶延迟函数[6]：

式中：Ts为控制周期。

由图2可知，逆变器控制环节开环函数为

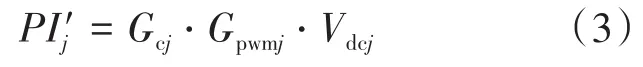
逆变器输出电压voj到电流i1j的传递函数为

2 现有诺顿等效模型

参考文献[7-8]忽略了PLL环节，任意第j台并网逆变器均可采用诺顿电路等效。即采用受控电流Nj·iref、并联阻抗ZNj等效，如图3所示。

图3 逆变器诺顿等效电路Fig.3 Equivalent circuit of gird-connected inveter

图3中，受控电流源Nj（s）的传递函数为

诺顿等效阻抗ZNj表达式为

式中：Z1j,CL为闭环阻抗。

由图3可知，并网电流i2j可表述为

3 含锁相环等效导纳模型

3.1 SOGI-PLL小信号模型

第2节所述诺顿等效方法，忽略了锁相环环节。但实际上，锁相环是并网逆变器的重要控制环节，对系统稳定性有重要影响[10-12]。为此，本文对现有诺顿等效电路模型进行修正，增加锁相环影响。但是，锁相环环节包含dq变换环节，dq变换为时域环节，无法直接获得其传递函数，需要对其进行小信号线性化处理。

SOGI-PLL是目前广泛使用单相锁相环[14-15]，其平均模型框图如图4所示。

图4 SOGI-PLL锁相环框图Fig.4 The block diagram of SOGI-PLL

图4中，SOGI滤波环节得传递函数为

式中：ks为自适应滤波器控制参数；ω为PCC电压角频率。

锁相环采用比例积分控制：

式中：kppll为比例系数；kipll为积分系数。

当PLL没有完全跟踪电网相位时，电网相位和锁相环输出相位存在相位差Δθ。即，dq变换所使用相位 θ1= θg+ Δθ，θg= ωt为电网电压相位。则dq变换可以拆分为TΔθ和Tθg，即

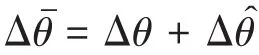
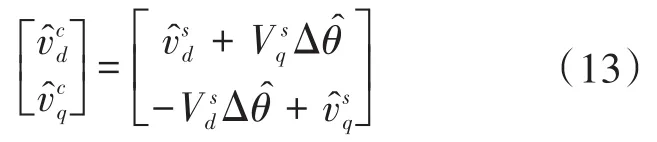
将式（14）代入式（13），联立可得：

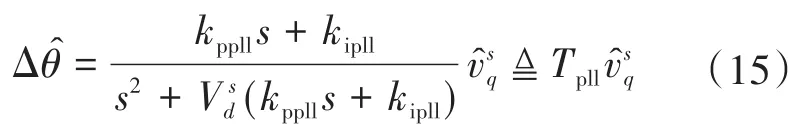
接下来，分析电网坐标系侧小信号传递函数。采用PARK逆变换，α-β坐标系和电网同步d-q坐标系下的小扰动分量可表述为

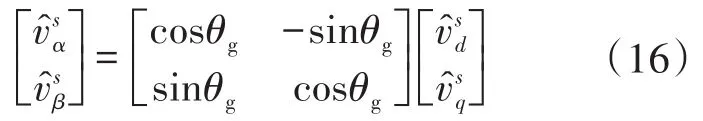
由式（15）可知，PLL环节中，扰动量vsd不起作用，故可忽略该扰动量。则式（16）简化为

对于拉普拉斯变换，存在：

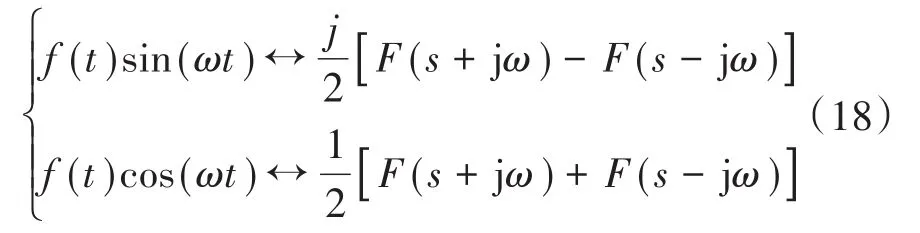
将式（15）代入式（17），并通过式（18）将式（17）变化到s域：

另外，参考电流iref可线性化为

3.2 多逆变器并网系统阻抗模型

将式（22）代入式（9），对于任意j台并网逆变器，考虑锁相环环节时，式（9）可改写为

为便于分析，定义新的锁相环导纳Ypllj：

则式（23）可改写为

由式（25）可知，当考虑SOGI-PLL时，单相并网逆变器的可采用导纳Yoj=YNj+Ypllj等效。相比原有诺顿等效阻抗方法，不含有等效电流源，并网逆变器完全采用阻抗Yoj等效。

依据式（25），图1所示n台单相逆变器并网系统的等效电路如图5所示。

Fig.5 含锁相环单相逆变器等效电路Fig.5 Equivalent circuit of single-phase inverter with PLL

依据图5，对于任意第j台并网逆变器，其并网电流i2,j：

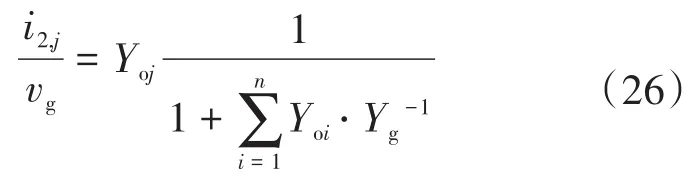
依据级联系统稳定性判别理论[16]，式（26）系统稳定需要满足两个条件：

1）Yoj自身稳定；

4 算例分析

本文算例单相并网逆变器参数与文献[7-8]一致。文献[7-8]未提供锁相环参数。为此，本文依据文献[15]典型设计方法，取阻尼比ς=0.7，带宽 ωb分别选取典型值 50 Hz，100 Hz，200 Hz。SOGI-PLL锁相环参数如表1所示。

表1 不同带宽SOGI-PLL锁相环参数Tab.1 Parameters of SOGI-PLL

4.1 阻抗对比稳定性分析

选取SOGI-PLL带宽100 Hz。单台逆变器的诺顿等效导纳YN，锁相环节等效导纳YPLL，和含锁相环等效导纳YO的波特图如图6所示。

图6 单台逆变器YN，YPLL，YO波特图Fig.6 Bode diagram of YN，YPLL，YOfor single inverter

由图6可知，YO和YN高频段曲线基本一致，YO和YPLL低频段曲线基本一致。锁相环导纳YPLL对YO的低频段特性具有决定性影响，且其低频段特性主要由YPLL确定。YPLL会增大低频段YO幅值增益，降低低频段稳定裕度。而高频段，YPLL对YO的影响不大，YO与YN曲线基本一致。

进一步观察式（7）可知，YN不含有锁相环和参考电流Iref信息，无法分析锁相环和参考电流大小对逆变器并网稳定性影响。但文献[10-12]中，对单台三相并网逆变器全阶小信号建模分析指出，锁相环和参考电流对逆变器的并网控制稳定性都有显著影响。

采用表1的SOGI-PLL参数，固定参考电流Iref=40 A，取不同锁相环带宽 ωb=200 Hz，100 Hz，50 Hz，等效导纳YO的波特图如图7所示。固定锁相环带宽100 Hz，选择不同参考电流Iref=20 A，40 A，60 A，逆变器等效导纳YO波特图如图8所示。

图7 不同锁相环带宽下YO波特图Fig.7 Bode diagram of YOwith different phase-locked loop bandwidths

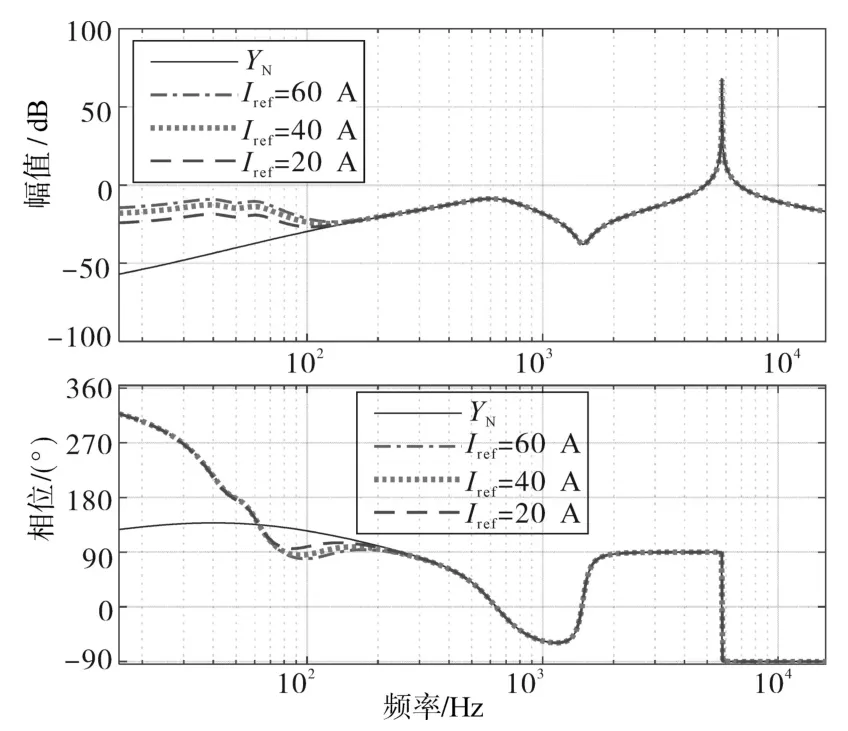
图8 不同参考电流时的YO波特图Fig.8 Bode diagram of YOwith different reference currents

由图7可知，锁相环带宽越低时，YO低频段幅值增益越低，低频段导纳越小，YO越接近YN，YO与YN重叠区域越多，稳定裕度越大。

由图8可知，当Iref越小时，YO导纳的低频段幅值增益越低，相位曲线越高，与YN重叠区域越大，系统稳定裕度越大。

4.2 可接入逆变器台数分析

对于n台逆变器并网系统，外部控制稳定性取决于导纳比（阻抗比）[7-8]。采用文献[7-8]参数，绘制导纳比奈奎斯特曲线，分析系统可接入最多逆变器台数。奈奎斯特曲线如图9所示。为简化篇幅，本文奈奎斯特图只给出（-1，0）附近的局部放大图。由图9可知，随着逆变器台数增加，奈奎斯特曲线越靠近（-1，0），并网系统控制系统稳定裕度越低。当逆变器台数n=63时，奈奎斯特曲线刚好跨过（-1，0），系统临界失稳。但是，后文含锁相环节等效导纳方法分析结果不同。

图9 诺顿等效方法奈奎斯特分析曲线Fig.9 Nyquist analysis curve using Norton equivalent method

采用本文所提考虑锁相环的等效导纳方法，分析导纳比奈奎斯特曲线，判断可接入逆变器台数。

图10为不同参考电流时奈奎斯特曲线。选取参考电流Iref=40 A，取不同锁相环带宽ωb=200 Hz，100 Hz，50 Hz，对应的导纳比奈奎斯特曲线如图10a～图10c所示。固定锁相环带宽100 Hz，取参考电流Iref=20 A，40 A，60 A时，对应的导纳比奈奎斯特曲线如图10d～图10f所示。

由图10可知，与诺顿等效方法分析一致，随着逆变器台数增加，导纳比奈奎斯特曲线逐渐靠近（-1，0），系统稳裕度降低。但是，临界失稳逆变器台数结论不一致。临界失稳逆变器台数小于63台，临界失稳逆变器台数受锁相环带宽和参考电流大小影响。

由图10a～图10c可知，不同锁相环带宽200 Hz，100 Hz，50 Hz时，临界失稳逆变器台数分别是15台、19台、25台。相比于诺顿等效方法分析结果，可接入逆变器台数明显减少。且随着PLL带宽降低，逆变器临界失稳逆变器台数增加。即，PLL带宽越低，系统稳定裕度越大，可接入逆变器台数越多。

图10 不同参考电流时奈奎斯特曲线Fig.10 Nyquist analysis curve with different reference currents

由图10d～图10f可知，参考电流分别为60 A，40 A，20 A时，临界失稳逆变器台数分别为13，19，36。随着参考电流降低，多逆变器并网系统稳定裕度增加，可接入逆变器数量越多。

5 RT-LAB仿真验证

RT-LAB为工业级的系统实时仿真平台，相比于普通数字仿真，其仿真步长与实际物理步长保持一致，具有更好的物理模拟效果。

为验证4.1节稳定性分析的结论，以图1为拓扑，采用文献[7-8]的逆变器参数及表1的锁相环参数，在RT-LAB实验平台上，搭建了n台单相逆变器并网实时仿真系统，进行仿真实验。图11为不同锁相环带宽和参考电流时仿真结果图。

图11 不同锁相环带宽和参考电流时仿真结果Fig.11 Simulation results with different PLL bandwidths and different reference currents

5.1 不同锁相环带宽仿真结果

与上小节分析相对应，单台并网逆变器参考电流设置为40 A，SOGI-PLL带宽分别选择200 Hz，100 Hz，50 Hz。1 s以前，系统接入逆变器数量为临界稳定台数；1 s时刻，通过断路器投入新的逆变器，破坏系统稳定性。

不同锁相环带宽和参考电流时的仿真曲线如图11所示。由图11a～图11c可知，1 s以前，并网电流稳定，多逆变器并网系统处于稳定。1 s时刻投入新逆变器，本文通过闭合断路器硬并网，并网初期存在较大冲击电流，经过约0.2 s后，冲击电流减少，并网电流出现低频振荡。

对于不同锁相环带宽，低频振荡频率不同。锁相环带宽200 Hz，100 Hz和50 Hz，对应的低频振荡频率分别为14.9 Hz，10.1 Hz和6.6 Hz，临界失稳台数分别为15，19和25。该结果本文方法分析结果一致，小于原有诺顿等效方法分析结果（63台）。随着锁相环带宽的降低，系统的稳定裕度增加，电网可接入逆变器台数越多，且失稳后低频振荡频率越低。

5.2 不同参考电流仿真结果

与上小节相对应，固定锁相环带宽100 Hz，分别给定参考电流Iref=20 A，40 A，60 A，进行多台单相逆变器仿真验证。不同参考电流的仿真结果如图11d～图11f所示。Iref=20 A时，系统进入稳定时间较长，修改为3 s时刻投入新的逆变器。

由图11d～图11f可知，参考电流分别为20 A，40 A和60 A时，临界失稳的逆变器台数分别是35，19和13，与4.1节稳定性分析结果一致。随着参考电流的增大，允许的接入并网逆变器数量减小。当失稳后，低频振荡频率分别为9.3 Hz，10.1 Hz，11.9 Hz，随着参考电流的增加，低频振荡频率增大。