SIDO Buck-Boost变换器的工作模式及稳态增益分析
2021-05-25谢锋皇金锋李林鸿
谢锋 ,皇金锋 ,2,李林鸿
(1.陕西理工大学电气工程学院,陕西 汉中 723001;2.陕西省工业自动化重点实验室,陕西 汉中 723001)
随着电力电子技术的飞速发展,开关电源逐渐朝着高频、小型化和多输出的方向发展[1-4]。单电感双输出DC-DC开关变换器仅使用一个电感(或高频变压器)就可以实现两路电压输出,这为需要多路电压供电的便携式电子设备提供了一个新的供电解决方案[5-7],因此SIDO DC-DC开关变换器受到国内外研究人员的广泛关注[8-9]。
SIDO Buck-Boost变换器具有宽输入及宽输出的特点,近年来,国内外的专家学者已经做了深入的研究工作,文献[10]提出了基于临界连续模式(critical conduction mode,CRM)的单电感双输出Buck-Boost PFC变换器,通过分时复用控制方法,实现了两个输出支路的独立控制。SIDO Buck-Boost变换器还具有升降压特性,因此SIDO Buck-Boost变换器不仅能够实现多路电压输出,而且能够实现多等级电压输出(相对于输入电源电压而言),这为需要多电压等级供电的电子产品供电问题提供了一个新的思路。但变换器设计时必须满足一定的条件,才能使得变换器严格地工作在预期设计的输出状态(升压或降压输出),而目前关于这方面的研究还未见报道。
SIDO Buck-Boost变换器的稳态增益与多个变量有关,实验结果表明,主开关和支路开关管的占空比均对变换器的稳态增益有较大影响,且与传统单输出Buck-Boost变换器相比,SIDO Buck-Boost变换器两支路的稳态增益不仅与占空比有关,也与两支路的负载阻值大小有关,因此,必须深入分析SIDO Buck-Boost变换器的稳态增益,明确其与占空比和负载等之间的关系,以便指导SIDO Buck-Boost变换器产品的开发与研制。
本文深入分析了CCM SIDO Buck-Boost变换器的稳态增益,得到了变换器工作在各种输出状态需满足的条件,并推导出了使得变换器增益取得极大值的实现条件。总结出了变换器稳态增益与主开关管和支路开关管占空比的关系。研究结果对于需要多等级电压输出的SIDO Buck-Boost变换器参数设计具有指导意义。
1 SIDO Buck-Boost变换器的工作模式
SIDO Buck-Boost变换器电路拓扑如图1所示,其由储能电感L,滤波电容Ca和Cb,主开关管Si,支路开关管Sa和 Sb,二极管VDa和 VDb以及负载电阻Ra和Rb组成,开关管Si,Sa和Sb的占空比Di,Da和Db满足Di<Db,Da+Db=1。
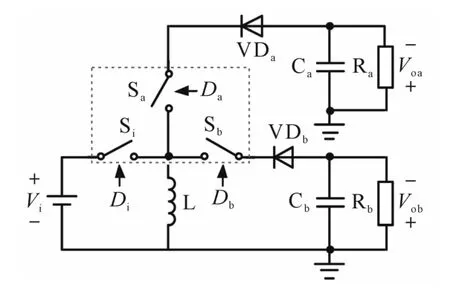
图1 SIDO Buck-Boost变换器电路拓扑Fig.1 The circuit topology of SIDO Buck-Boost converter
根据最小电感电流与零的大小关系,可将SIDO Buck-Boost变换器的工作模式分为连续导电模式和不连续导电模式,下面进行详细分析。
1)连续导电模式(CCM):CCM工作波形如图2所示,此时ILV>0。在0~t1时间段,输入电源Vi向电感L充电;在t1~t2时间段,电感向负载Rb供电的同时为电容Cb充电;在t2~t3时间段,电感向负载Ra供电的同时为电容Ca充电。图2中ILP为最大电感电流,ILT为转折电感电流,ILV为最小电感电流。

图2 CCM工作波形Fig.2 Working waveforms of CCM
2)不连续导电模式(DCM):DCM工作波形如图3所示,此时ILV=0。在0~t1时间段,输入电源Vi向电感L充电;在t1~t2时间段,电感为负载Rb供电的同时为电容Cb充电。在t2~t2A时间段,电感电流iL由ILT开始下降,当iL>Ioa时,电感L为负载Ra供电的同时为电容 Ca充电,直到 iL<Ioa,电容 Ca和电感共同向负载Ra供电。在t2A~t3时间段,电感电流为零,负载由电容供能。

图3 DCM工作波形Fig.3 Working waveforms of DCM
2 CCM SIDO Buck-Boost变换器的稳态关系
2.1 电感电流关系
SIDO Buck-Boost变换器稳态工作时,电感电流平均值IL有如下关系成立:
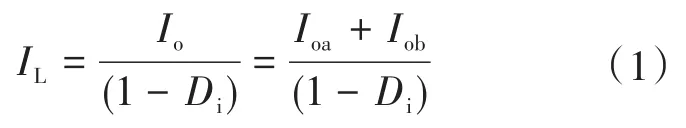
又因为输出电流Ioa=Voa/Ra,Iob=Vob/Rb,因此可得电感电流平均值为
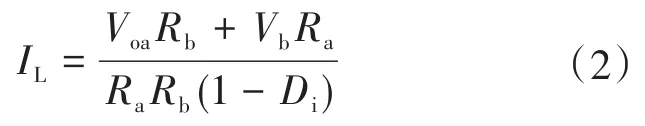
式中:Voa,Vob分别为支路a和支路b的输出电压;Ra和Rb分别为支路a和支路b的负载电阻。
结合图2可得:

式中:Vi为输入电压。
2.2 临界电感
当SIDO Buck-Boost变换器工作于CCM与DCM的临界状态时,最小电感电流ILV为零,得到CCM与DCM的临界电感LC为

式中:f为开关频率。
分析式(4)可知,当L>LC时,变换器工作于CCM;当L<LC时,变换器工作于DCM。
2.3 稳态增益
根据状态空间平均法[11-12],得到CCM SIDO Buck-Boost变换器两条支路的稳态增益为
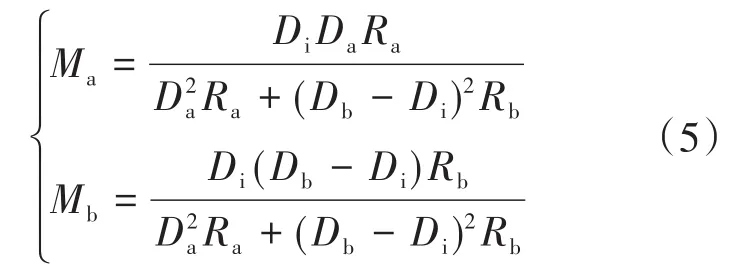
其中

分析式(5)可知,SIDO Buck-Boost变换器的稳态增益不仅与占空比有关,而且与负载阻值有关,因此SIDO Buck-Boost变换器在不同的占空比及负载条件下,其稳态增益会出现大于1、小于1和等于1的情况,即变换器两支路输出会出现升压、降压、电源电压和升降压的情况,下面对这几种情况进行详细分析。
3 CCM稳态增益分析
SIDO Buck-Boost变换器CCM时,其输出处于升压和降压状态的临界条件为主开关管Si的占空比 Di=0.5,下面就Di<0.5,Di=0.5和Di>0.5 这三种情况分别进行讨论。
3.1 Di<0.5时稳态增益分析
假设Db=1,则Da=0,此时SIDO Buck-Boost变换器的能量全部转移到b支路,因此,b支路的稳态增益处于最大值:

因此,当主开关管Si的占空比Di<0.5时,无论支路开关管Sa和Sb的占空比Da和Db如何改变,变换器两支路必工作在降压状态。
3.2 Di=0.5时稳态增益分析
主开关管Si的占空比Di=0.5时,式(5)可简化为

3.2.1 升压输出状态
变换器两支路输出为升压状态时,稳态增益满足:
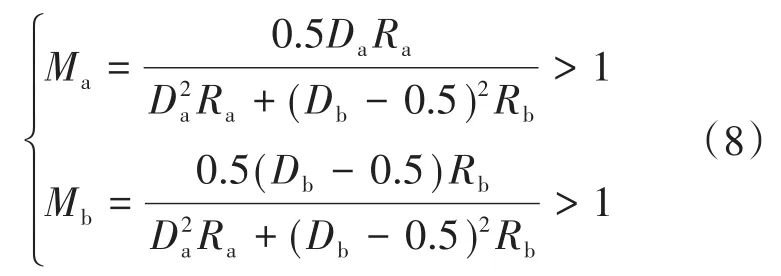
解得式(8)两个不等式的交集为空集,因而此时变换器两支路不能同时工作在升压状态。
3.2.2 降压输出状态
变换器两支路输出为降压状态时,稳态增益满足:

解得式(9)两个不等式解的交集为空集,因而此时变换器两支路不能同时工作在降压状态。
3.2.3 电源电压输出状态
变换器两支路输出为电源电压状态时,稳态增益满足:
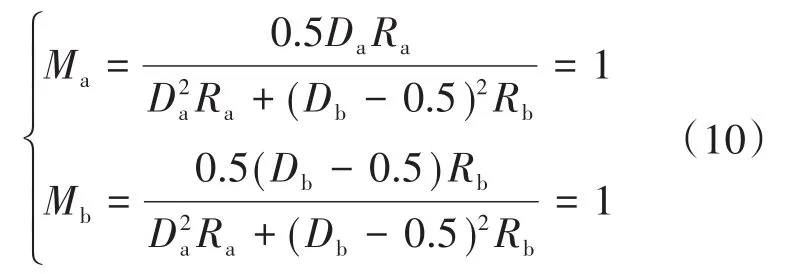
求解式(10)可得:

因此只需满足式(11),变换器两支路就可以工作在电源电压状态。当Ra=Rb时,式(11)可简化为

3.2.4 升降压输出状态
变换器两支路输出为升降压状态时,(假设支路a降压,支路b升压),稳态增益满足:

求解式(13)可得:

此时,变换器两支路分别工作在降压和升压状态。当Ra=Rb时,式(14)可简化为

3.3 D ii>0.5时稳态增益分析
3.3.1 升压输出状态
变换器两支路输出为升压状态时,稳态增益满足:

求解式(16)可得:

此时变换器两支路同时处于升压状态。当Ra=Rb时,两支路同时处于升压的条件为

3.3.2 升降压输出状态
变换器两支路输出为升降压状态时(假设支路a降压,支路b升压),稳态增益满足:

求解式(19)可得:

此时变换器两支路处于升降压状态。当Ra=Rb时,变换器两支路处于升降压状态的条件为

同理可以证明,此时不存在使得变换器两支路同时工作在降压状态的条件。也不存在使得变换器两支路同时处于电源电压状态的条件。
根据以上分析可知,当主开关管占空比Di<0.5时,SIDO Buck-Boost变换器两支路必工作在降压状态;当主开关管占空比Di=0.5时,SIDO Buck-Boost变换器两支路可以工作在电源电压状态,也可以工作在升降压状态,但不能同时工作在升压状态,也不能同时工作在降压状态;当主开关管占空比Di>0.5时,SIDO Buck-Boost变换器两支路输出可以工作在升压状态,也可以工作在升降压状态,但不能同时工作在电源电压状态,也不能同时工作在降压状态。
4 稳态增益极值分析
4.1 支路a稳态增益极值分析
将式(5)中Ma对Di求偏导可得:

式(22)表明,支路a的稳态增益随着Di的增大而增大。
将式(5)中Ma对Db求偏导可得:

令式(23)等于零,解得Db为

将Ma对Db求二阶偏导并将式(24)代入可得:

由式(25)可知,当Db取值满足式(24)时,支路a的稳态增益取得极大值。此时的Db就是使得支路a稳态增益取得极大值的极大值点。
4.2 支路b稳态增益极值分析
将式(5)中Mb对Di求偏导可得:

式(26)表明,支路b的稳态增益随着Di的增大而增大。
将式(5)中Mb对Db求偏导可得:

令式(27)等于零,解得Db为
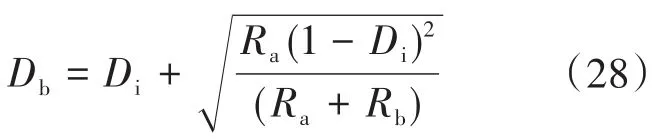
将Mb对Db求二阶偏导并将式(28)代入可得:

由式(29)可知,当Db取值满足式(28)时,支路b稳态增益取得极大值。此时的Db就是使得支路b稳态增益取得极大值的极大值点。
根据以上分析可知,SIDO Buck-Boost变换器的稳态增益随着主开关管占空比Di的增大而增大;并且两个支路开关管占空比分别存在一个极大值点,在此极大值点,变换器此支路稳态增益取得极大值。
5 实验分析
为验证理论的正确性,搭建了实验电路。
变换器参数设置如下:输入电压Vi=10 V,开关频率f=20kHz,负载电阻Ra=Rb=20 Ω,滤波电容Ca=Cb=40 μF。
5.1 工作模式实验分析
设定变换器的占空比为:Di=0.4,Da=0.3,Db=0.7,将参数代入式(5)中,解得支路a和支路b两支路输出电压均为6.67 V,再将参数代入式(4)中,可得CCM与DCM的临界电感LC为90 μH。因此实验电感L分别取1 mH和60 μH,得到实验波形如图4所示。由图4a可知,当电感取1 mH时,最小电感电流ILV>0,因此变换器工作在CCM。由图4b可知,当电感取60 μH时,最小电感电流ILV=0,因此变换器工作在DCM。实验结果与理论分析一致,验证了变换器工作模式分析的正确性。

图4 工作模式实验波形Fig.4 Experimental waveforms of working modes
5.2 稳态增益实验分析
根据主开关管占空比Di取值的不同,变换器两支路将会工作在不同的状态。
分别取Di=0.4,Di=0.5和Di=0.6三种情况进行实验,得到实验波形如图5~图7所示,实验得到的输出电压数据如表1所示。由图5可知,当Di=0.4时(小于0.5),变换器两支路均工作在降压状态。由图6可知,当Di=0.5,Db=0.75时,变换器两支路工作在电源电压状态(由于电路损耗等原因,实际输出电压略小于电源电压);Di=0.5,Db=0.85时,支路a工作在降压状态,支路b工作在升压状态(变换器工作在升降压状态)。
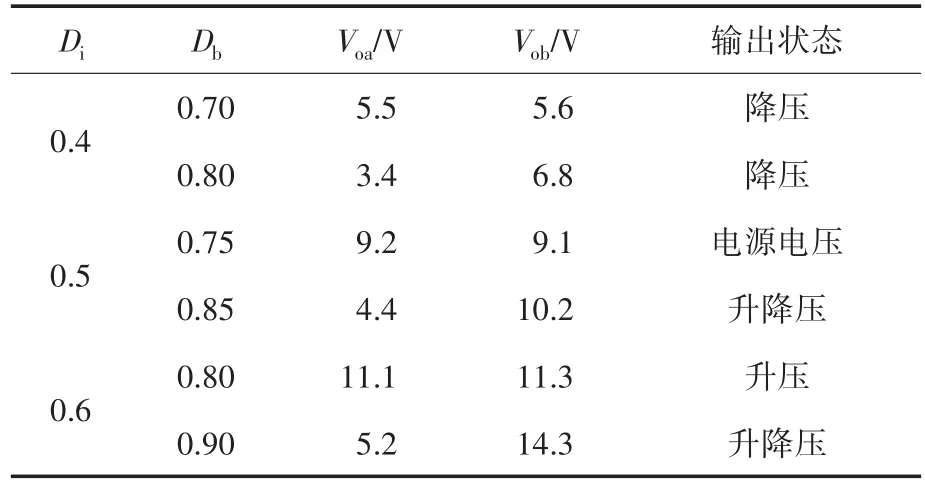
表1 输出电压数据Tab.1 Output voltage data

图5 Di=0.4时稳态输出电压Fig.5 Steady output voltage at Di=0.4

图6 Di=0.5时稳态输出电压Fig.6 Steady output voltage at Di=0.5

图7 Di=0.6时变换器稳态输出电压Fig.7 Steady output voltage at Di=0.6
由图7可知,当Di=0.6,Db=0.8时,变换器两支路工作在升压状态;Di=0.6,Db=0.9时,支路a工作在降压状态,支路b工作在升压状态(变换器工作在升降压状态)。
由实验结果和实验数据可得,变换器工作在CCM时,若主开关管的占空比小于0.5,SIDO Buck-Boost变换器两支路只能工作在降压状态;若主开关管的占空比等于0.5,变换器两支路可以同时工作在电源电压状态,也可以工作在升降压状态,但不能同时工作在升压状态,也不能同时工作在降压状态;若主开关管的占空比大于0.5,变换器两支路可以同时工作在升压状态,也可以工作在升降压状态,但不能同时工作在降压状态。
以上实验结果与理论分析一致,验证了理论分析的正确性。
6 结论
本文讨论了SIDO Buck-Boost变换器的工作模式,深入分析了CCM时变换器的稳态增益,根据主开关管占空比取值与0.5之间关系的不同,变换器两支路的稳态增益会出现四种不同的情况。变换器两支路的稳态增益均随着主开关管占空比的增大而增大,且两支路的支路开关管占空比分别存在一个极大值点,在此极大值点,变换器此支路的输出稳态增益取得极大值。
本文分析所得结论可以为需要多电压等级输出的SIDO Buck-Boost变换器的研制提供理论指导。
