双水平井斜井段导向钻井快速磁测距计算方法
2021-05-25刁斌斌高德利
刁斌斌, 高德利, 穆 凡, 张 森
(中国石油大学(北京)石油工程教育部重点实验室,北京 102249)
蒸汽辅助重力泄油(SAGD)双水平井技术由Butler和Stephens[1]提出以来,已在重油和油砂的开发中得到了广泛应用,同时在未来天然气水合物的高效开发中也具有潜在的应用前景。目前,SAGD双水井钻井技术在中国辽河油田和新疆风城油田等重油开发矿场试验中效果显著[2-5]。但是现场实践中发现,仅在注入井水平井段使用磁导向钻井技术,仍难保障整个水平井段的邻井距离都达到设计要求,亟需在注入井斜井段实现磁导向钻井[6]。目前,可以用于引导注入井沿生产井平行钻进的工具主要是MGT(magnetic guidance tool)[7-8]和RMRS(rotating magnet ranging system)[8-9]。中国对该类工具的研究起步较晚,特别是研发的基于旋转磁场随钻测量的测距导向技术已在钻井现场取得应用实效[10-14]。为了实现在注入井斜井段实现磁导向钻井,研究者提出了考虑会聚角和异面夹角影响的RMRS测距算法[15]。然而,该方法需要磁短节随钻头钻进一段距离才能得到正钻井到已钻井的距离和方向,需要钻进的距离随邻井距离的增加而增加,不仅增加了钻井周期,而且钻进方向的改变和磁短节井下位置的记录误差也会影响计算结果的精度。针对以上问题,笔者以TSP-RMRS[16]用于双水平井水平井段测距算法为基础,进一步探讨考虑会聚角和异面夹角的TSP-RMRS测距算法,以实现双水平井斜井段空间相对位置的快速测量。
1 TSP-RMRS的工作原理
与RMRS的硬件组成相似,TSP-RMRS的硬件也主要由磁短节、探管、接口箱和计算机组成。如图1所示,与RMRS不同的是,TSP-RMRS探管的内部有两个三轴交变磁场传感器、一个三轴重力加速度传感器,其中一个三轴交变磁场传感器靠近探管的止端,另一个三轴交变磁场传感器和三轴重力加速度传感器靠近探管的接线端,而且两个交变磁场传感器之间相隔一定的距离d[16]。如图2所示,测量时,磁短节直接与钻头相连,在注入井中随钻头的旋转而旋转,但是不需要沿井眼延伸方向移动;探管由井下牵引器或修井油管等下入预先钻好的生产井中,主要作用是探测井下的地磁场、重力场、温度和由磁短节旋转产生的两组交变磁场感应强度三轴分量数据,并将记录的数据通过电缆传输到地面的接口箱,进而传输到计算机中安装的测距导向计算软件,计算注入井与生产井的空间相对位置;然后,结合注入井与生产井的测斜数据,定向井工程师可以不断调整注入井的井眼轨迹按设计要求钻进。

图1 探管内部三轴传感器排列示意图Fig.1 Arrangement diagram of all three-axis sensor in probe

图2 TSP-RMRS工作示意图Fig. 2 Operational diagram of TSP-RMRS
2 双水平井快速磁测距算法

图3 磁短节与探管的空间位置关系Fig.3 Spatial position relation between magnetic sub and probe
在双水平井斜井段,两口井不断靠近,而且并不总是在同一平面上,可以把这两口井斜井段的空间位置关系分解为共面会聚和异面两种情况,并可以用会聚角α表征两口井测量井段的会聚程度,用异面夹角β表征两口井测量井段的异面程度[15]。如图3所示,以磁短节的中心为原点O,以井眼延伸方向为w轴,以磁短节到已钻井的径向为r轴,q轴同时正交于w轴和r轴,建立O-rqw坐标系;以磁短节到传感器组Ⅰ的径向为r1轴,q1轴同时正交于w轴和r1轴,建立O-r1q1w坐标系;以磁短节到传感器组Ⅱ的径向为r2轴,q2轴同时正交于w轴和r2轴,建立O-r2q2w坐标系。传感器组Ⅰ在O-r1q1w坐标系中的坐标为(r1, 0,w1);传感器组Ⅱ在O-r2q2w坐标系中的坐标为(r2, 0,w2)。
由磁短节产生的磁场感应强度在传感器组Ⅰ处的r1轴和w轴分量的幅值[16]可表示为

(1)

(2)
同理,由磁短节产生的磁场感应强度在传感器组Ⅱ处的r2轴和w轴分量的幅值可表示为

(3)

(4)
令

(5)

(6)
由式(1)、(2)和(5)可得

(7)
式中,当w1>0时,取“+”号;当w1<0时,取“-”号。
由式(3)、(4)和(6)可得

(8)
式中,当w2>0时,取“+”号;当w2<0时,取“-”号。
如图4所示,以探管上端传感器组中心为原点,以注入井井眼高边方向和延伸方向分别为h1轴和w1轴,l1轴同时正交于h1轴和w1轴,建立h1l1w1直角坐标系;h1轴到u1轴的夹角Ahu1为135°,v1轴同时正交于u1轴和w1轴,建立u1v1w1直角坐标系。以探管上端三轴磁通门传感器的三个轴建立x1y1z1直角坐标系,其中z1轴与探管的轴线重合,并指向探管尾端。
由探管上端传感器组检测到的由磁短节产生磁场的三轴磁感应强度分量Bx1、By1和Bz1可得

(9)
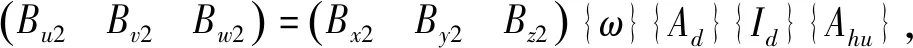
(10)

(11)

(12)
其中

式中,ω为探管重力工具面角,(°);Ip和Ii分别为生产井和注入井的井斜角,(°);Ap和Ai分别为生产井和注入井的方位角,(°)。

图4 磁短节与传感器组Ⅰ的相对方位Fig.4 Relative orientation between magnetic sub and sensor package Ⅰ
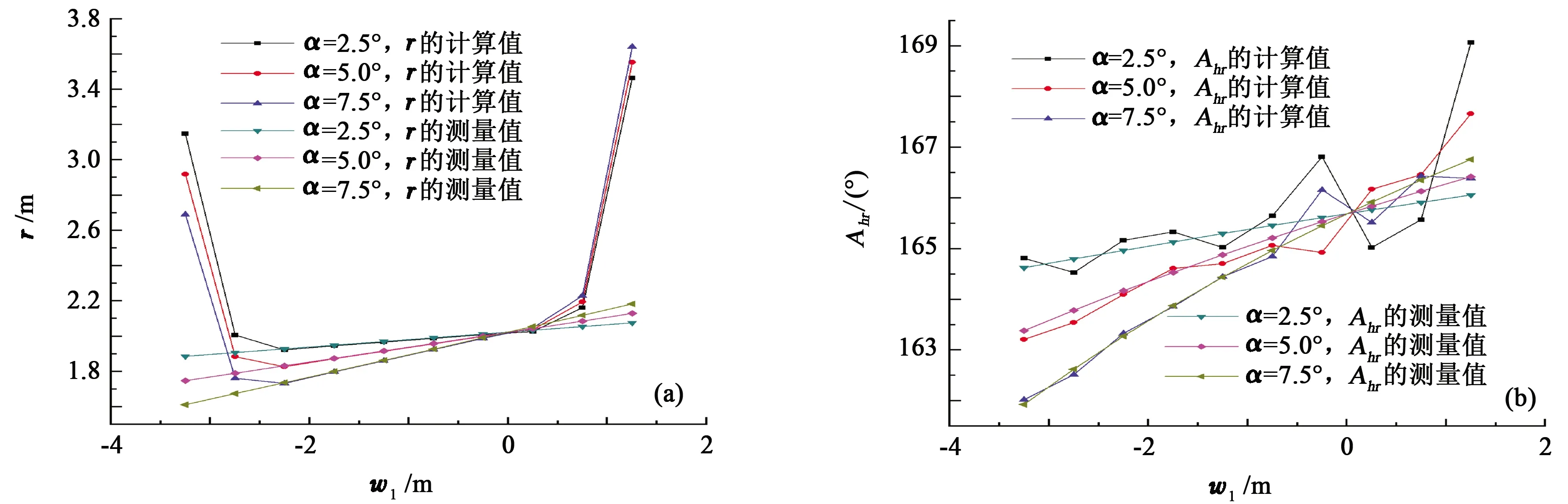
由SAGD双水平井设计轨道的要求可知,0 (13) 由式(13)和角Ahu1可得h1轴到r1轴夹角Ahr1为 (14) 即 (15) 同理可得 (16) 当SAGD双水平井斜井段共面会聚(α>0,且β=0)时,r轴、r1轴和r2轴共面。如图5所示,点A和B分别代表传感器组Ⅰ和Ⅱ的中心点;点A和B在w轴上的投影分别为点M和N;线段EF平行于h轴;线段EF垂直于线段BF;g轴指向点A的铅垂线方向。在O-rqw坐标系中,点A、B、M、N和E的坐标分别为(r1,0,w1)、 (r2,0,w2)、(0,0,w1)、(0,0,w2)和(r1,0,w2)。 图5 两口井斜井段共面会聚时磁短节与 探管相对位置的计算模型Fig.5 Computational model for relative position between magnetic sub and probe when build-up sections of SAGD wells being coplanar 由图5可知: γ=180°-Ahr2, (17) δ=Ii+φ, (18) cosα=cosθcosφ, (19) cosIp=cosθcosδ, (20) (21) 由式(16)~(18)可得 (22) 由式(15)~(19)可得 (23) 联立式(22)和(23)即可求得α。同时,由图5可知: w2-w1=dcosα, (24) r1=r-w1tanα, (25) r2=r-w2tanα. (26) 联立式(5)、(6)和(22)~(24)可得 (27) (28) (29) 由于此时两口井的测量井段共面,因此正钻井井眼高边方向到r的夹角Ahr等于Ahr1和Ahr2的值。 当SAGD双水平井斜井段异面(α=0且β>0)时,如图6所示。在O-rqw坐标系中,点C和D的坐标分别为(r,0,w1)和(r,0,w2)。 图6 两口井斜井段异面时磁短节与探管相对 位置的计算模型Fig.6 Computational model for relative position between magnetic sub and probe when build-up sections of SAGD wells being no-coplanar 由图6可知: (30) 式中,LAC和LBD分别为线段AC和BD的长度。 (31) (32) η1+η2=|Ahr1-Ahr2|, (33) w2-w1=dcosβ, (34) (35) LAC=rtanη1, (36) LBD=rtanη2, (37) (38) 联立式(5)、(6)、(31)和(32)可得 (39) (40) 联立式(30)、(39)和(40)可得 (41) 结合η1和η2的取值范围,联立式(33)和(41)可求得η1和η2。将求得的Ahr1、角Ahr2和η1的值代入式(38),即可求得角Ahr。 由式(35)~(37)可得 r(tanη1+tanη2)=dsinβ. (42) 联立式(34)、(39)和(40)可得 (43) 联立式(42)和(43)可得 (44) 将求得的k1、k2、η1、η2以及d代入式(44)即可求得正钻井到探管径向间距r。 如图7所示,模拟磁短节和测试小车都放到无磁支架上,探管放于支架下方。测试小车可以带动模拟磁短节旋转,从而模拟磁短节随钻头在井下旋转。测量过程中无磁支架不动,模拟磁短节摆放的倾斜角为90.3°、方位角为192°,并通过调整探管摆放的姿态改变会聚角α和异面夹角β。每次测量时,磁短节都在测试小车的驱动下以一定的角速度旋转,测试小车在无磁支架上不移动。每次测量后,测试小车在无磁支架上移动0.25 m。 当模拟两口井斜井段共面会聚且α等于5°、角β等于0°时,探管检测到的z轴(即探管的轴线方向)磁感应强度信号如图8所示。由图8可知,每次测量得到的z轴磁感应强度信号的幅值基本保持不变。因此无法由z轴磁感应强度信号的幅值定性判断两口的会聚/发散和异面的程度。 图7 试验中的TSP-RMRS模拟装置Fig.7 Simulated TSP-RMRS in experiment 图8 探管记录的轴向磁感应强度随时间的变化Fig.8 Variation in axial magnetic induction intensity over time recorded by probe 当β等于0°、α取不同值时,模拟磁短节到探管径向间距r和角Ahr的计算值与真实值,结果如图9所示。当角α等于0°、角β取不同值时,模拟磁短节到探管径向间距和Ahr的计算值与真实值如图10所示。由图9和10可知,w1的变化对模拟磁短节到探管径向间距r的计算精度具有很大影响,然而w1的变化对Ahr的计算精度影响较小;当探管检测到的信号具有较好质量时,模拟磁短节到探管径向间距对r和Ahr的计算精度影响较小;当-d≤w1≤0时,模拟磁短节到两组传感器的轴向距离同时小于等于两组传感器的间距,此时由本文中介绍的测距算法得到的r和Ahr都具有很好的计算精度。在实际应用中,可以通过调整探管下放井深,达到磁短节到探管内部两组传感器的轴向距离同时小于等于两组传感器间距的目标。因此本文中的测距算法可以用于SAGD双水平井导向钻井工程。同时,综合考虑SAGD双水平井设计间距、探管井深测量误差和探管结构的抗弯强度,建议探管内部两组传感器的间距d设计为5 m。 图9 α不同时r和Ahr的计算值与真实值Fig.9 Calculated and measured values for r and Ahr with different α values 图10 β不同时r和Ahr的计算值与真实值Fig.10 Calculated values and measured values for r and Ahr with different β values (1)SAGD双水平井斜井段邻井距离的精确测量与精细控制,有利于进一步提高两口井水平井段邻井距离的控制效果,而建立考虑斜井段两口井非平行空间位置关系的磁测距算法是实现斜井段邻井距离精确测量的关键。 (2)提出的考虑会聚角和异面夹角影响的TSP-RMRS测距算法,适用于SAGD双水平井斜井段邻井距离的测量,同时不需要磁短节随钻头钻进一段距离,有利于提高邻井距离的计算精度。 (3)当磁短节到探管内部两组传感器的轴向距离同时小于等于两组传感器的间距时,SAGD双水平井斜井段的TSP-RMRS磁测距算法的计算精度可以满足钻井现场的实际需求。



2.1 共面会聚



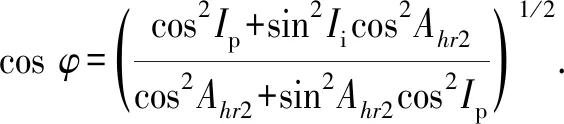



2.2 异 面




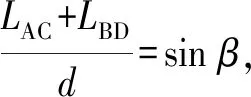






3 模拟试验结果



4 结 论
