电场诱导微结构成型的模拟研究

韩志亮，刘学清

（江汉大学 光电化学材料与器件教育部重点实验室，湖北 武汉 430056）

0 引言

随着光电器件柔性化和尺寸微型化，表面具有微纳结构的柔性聚合物薄膜由于其特殊的光、电和量子效应，在微器件中具有潜在的应用价值和广泛研究前景［1-5]。而微纳结构的加工技术是器件量产化的制约因素，传统的微纳结构主要通过机械压印实现。近年来，利用电场技术构建聚合物微结构逐渐得到关注［6-10]，如文献［11-14]研究了PDMS在电场诱导成型过程中各工艺参数对结构的影响及微透镜阵列结构；文献［15-18]通过电场诱导设计了高保真度、高宽比的微通道实验结构。目前报道的文献中，大多数研究集中在加工工艺的实验控制和参数优化，这种定性和半经验式研究方法难以预测微纳结构生长趋势和结构成型的精确控制，因此很难得到预期的结构。

随着计算仿真技术的发展，利用软件模拟微结构加工过程，定量分析工艺参数（电场、极板间距、聚合物初始膜厚）与微结构形貌之间的关系并预测实验结果逐渐得到重视。本文采用相场法瞬态仿真分析数学模型，讨论了微结构的成型过程及原理，采用COMSOL Multiphysics软件对电场诱导过程进行了仿真模拟，分析了电极宽度、电压及聚合物初始膜厚对最终结构生长和演化的影响，分别采用相场法与水平集法模型进行仿真并对仿真结果进行了比较。

1 电场诱导聚合物流变成型机理

电场诱导聚合物流变成型技术是一种非接触式聚合物微结构成型技术，利用一定电场强度下的静电场力作用驱使聚合物表面的微热扰动不断演化生长，最终形成具有特定形状的微结构。目前存在如图1所示的3种诱导方式：利用平板模板与微热扰动聚合物在静电场中形成与最不稳定波长相符的微结构（图1（a））；利用预结构化聚合物与平面模板进行诱导成型(图1（b）)；利用预结构化模板与平面聚合物诱导成型（图1（c）)。

图1 电场诱导成型结构图Fig.1 Str uctur e of electric field induction molding

1.1 均匀电场诱导成型最不稳定波长

根据多相液体界面的微观规律可知，在自然状态下，聚合物在微观尺度下表面非完全水平，在范德华力和重力作用下存在极小幅度的微热扰动波，具有一定波长。在均匀电场作用下，一部分扰动波被加强，一部分被抑制，其中生长速度最快的波长称为最不稳定波长，随着最不稳定波长的扰动增强，导致聚合物薄膜按照最不稳定波长向上生长［19]。根据生长与抑制的临界波数与波长的关系以及生长速率与波数的关系，可求得临界生长微观热扰动波数km及最不稳定波长λm的计算公式为

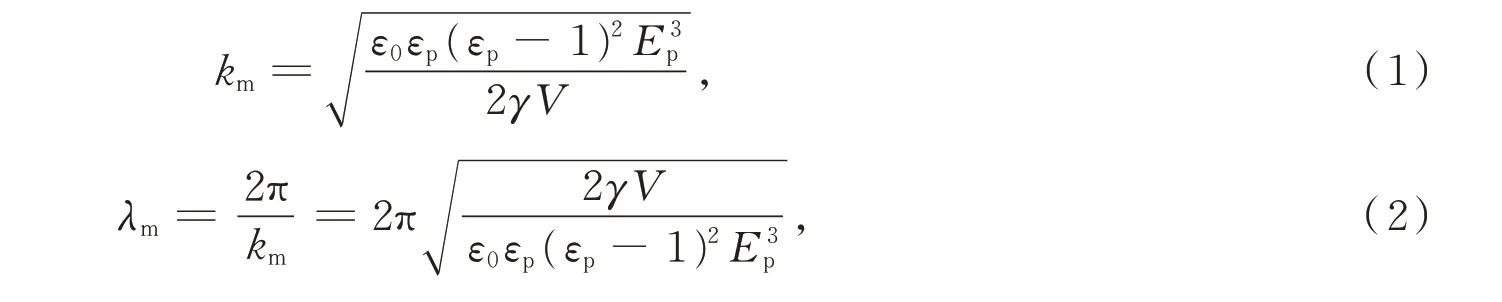
式中，ε0表示真空介电常数，F/m；εp表示聚合物相对介电常数，无因次；Ep表示聚合物中的空间调制电场强度，V/m；γ表示聚合物表面张力系数，N/m；V表示电压，V。

1.2 均匀电场诱导电流体力学基础

对电流体动力学分析理想化温度与材料属性不变。外加电场作用时平面模板诱导聚合物满足麦克斯韦应力张量方程产生的静电压强，忽略磁场影响，模拟简图如图2所示。当在模板与基底之间施加电压时，内部产生均匀场强，根据场内电势与高度的关系可知：

式中，Ea表示空气中的空间调制电场强度，V/m；H表示模板底面与基底表面的距离，m；h表示平面聚合物的厚度，m。

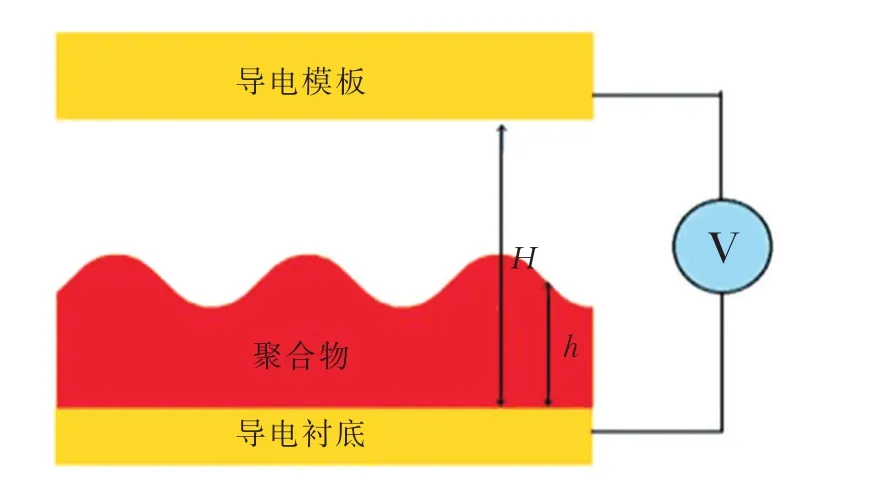
图2 模型简图Fig.2 The model diagram

在气-液界面处，由于聚合物内部不存在自由电荷，聚合物与空气的电位移矢量相等，且两侧的电势相等，因此有

式中，n表示气-液界面法向方向且指向空气一侧；φa表示空气电势，V；φp表示聚合物电势，V。

根据（3）式和（4）式，可求得Ea和Ep分别为

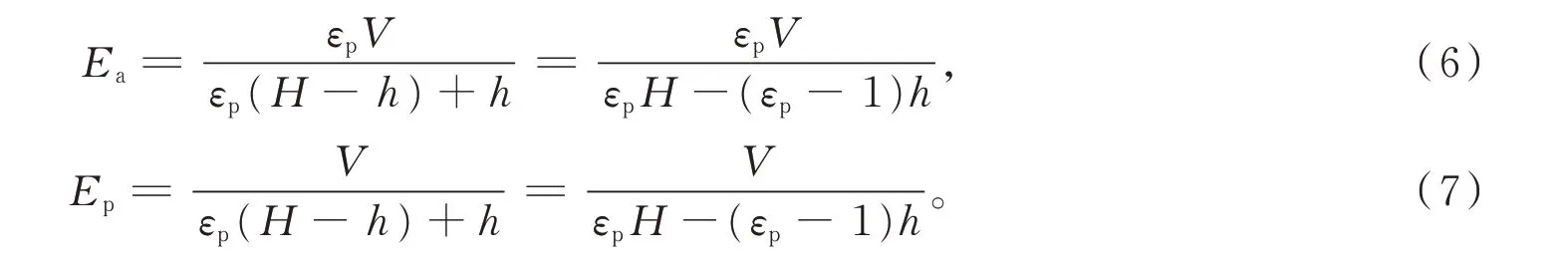
由麦克斯韦方程可知，在气-液界面处空气与聚合物满足力学平衡，当连续两介子的介电常数与磁导率不同时，界面处会产生麦克斯韦应力张量效应，始终沿界面法线方向指向介子内部，根据界面处麦克斯韦张量方程有

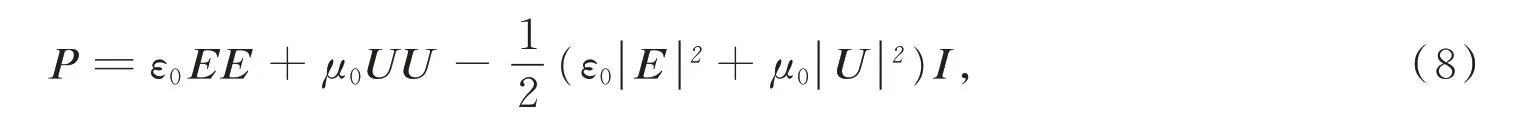
式中，P表示麦克斯韦张量，Pa；μ0表示真空磁导率，N/A2；E表示空间电场矢量，V/m；U表示空间磁场矢量，A/m；I表示单位矩阵。

因为无磁场存在，因此麦克斯韦张量方程可简化为（9）式，且在空气与聚合物一侧所受的麦克斯韦张量沿法线指向空气和聚合物分别为

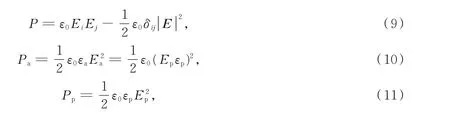
式中,E i和E j分别表示水平和垂直电场分量；δij表示克罗内多算子；Pa表示空气一侧所受静电张量，Pa；Pp表示聚合物薄膜一侧所受静电张量，Pa；εa表示空气相对介电常数，无因次。

根据（10）式和（11）式可得聚合物与空气在界面处所受的静电张量差值沿竖直方向指向模板，在诱导过程中聚合物内部产生的麦克斯韦压强为

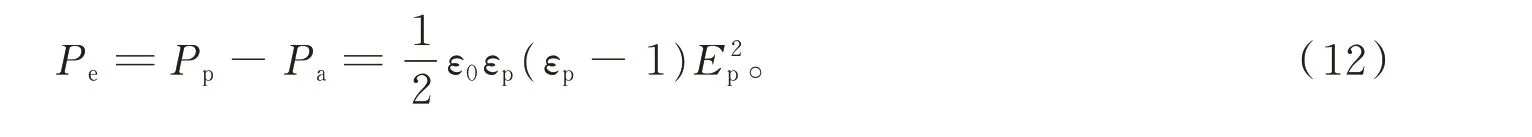
当聚合物在自然状态时，会产生一定波长热扰动。施加外部电场后，聚合物的热扰动在波峰与波谷不同位置处会产生不同的静电压强（见图3）。

根据（7）式和（12）式聚合物空间调制电场强度可得

再由流体静力学分析，聚合物内部受总压为

式中,P0表示大气压强，Pa；Pγ表示界面表面张量压强，Pa；P A和P B分别表示A点和B点的总压强；PeA和PeB分别表示A点和B点的麦克斯韦张量压强，Pa。

根据图3中A点与B点处聚合物厚度及场强不同（h A＞h B，E A＞E B），可推出波峰A点处聚合物压强比波谷B点处聚合物压强小，在静电压强作用下，B点处聚合物会不断向A点处流动，波峰处聚合物会不断演化生长，随着高度升高，压强差增大，生长速度也会增加直至波谷处聚合物全部聚集在波峰处。

当以光滑模板进行诱导时，靠微热扰动波的压强差成型；若以图案模板诱导时，由于模板图案的不均匀导致内部场强不一样，图案下压强作用会克服聚合物微扰动产生作用按图案的形状成型，成型原理与光滑模板一样。

2 模拟结果与分析

采用有限元软件COMSOL Multiphysics模拟分析，选择相场法对微结构变形进行研究，以相场作为流场与静电场基础，利用相场函数追踪聚合物-空气界面的演化变形。由于无法实现微热扰动状态模型，采用结构化电极模板进行模拟研究，探索工艺参数对聚合物微结构变形的影响，简图如图2所示。

2.1 电极宽度对微结构的影响

为简化计算，模拟采用半个周期对称二维模型进行仿真。电极微结构宽度分别采用8、14、20μm，聚合物膜厚采用10μm，电压为800 V。图4为聚合物表面变形过程及不同电极结构间隙对微结构变形的影响。蓝色为空气，红色为聚合物，白色凹陷部分为电极轮廓结构（几何结构未表示）。

图4 不同电极宽度对微结构影响Fig.4 Effects of electrode width on microstructure

由图4可知，当电场作用时间在2e-4s时，微结构变形较明显，电极宽度为20μm的聚合物生长高度最大，而8与14μm均出现微结构趋势但增长较慢。对比不同电极宽度对微结构的影响可以看出，在一定程度上增加电极宽度可以影响微结构生长速度；根据电场模曲线图可以看出，电极宽度越大，聚合物空气界面初始场强越大，而电场强度差是产生静电压强差的主要因素，因此电极宽度在一定程度上会影响微结构高度。

2.2 电压对微结构的影响

从（13）式可以看出，电压是影响微结构高度很重要的外部因素，电压直接对聚合物表面的场强分布产生影响，从而影响诱导过程。笔者主要分析不同电压对聚合物微结构成型的影响，电极宽度采用20μm，其他尺寸保持不变，分别采用550、700、850 V不同电压仿真分析对微结构形貌变化的影响。在诱导时间2.4e-4s时，聚合物表面结构如图5所示，根据微结构的最终态可以看出，在电压为550 V时，聚合表面只有轻微的变化波动，而在700 V时，微结构有明显的波形，但高度较低；当电压增加至850 V时，微结构波峰高度增加接近电极表面，若继续增加电压则可使微结构与电极接触，变化见图5。

同时，可以推导出电压直接影响微结构最终高度变化，若电压较低则无法克服聚合物表面张力及重力形成微结构。通过对比图5中电场模曲线图可以看出，当电压为550 V时，电极凸起部分与平板部分电场模相差较小，当电压逐渐增大时，凸起部分的场强差也逐渐增大从而更有利于微结构成型，同时微结构成型速度也会减慢；若增加电极凸起部分的长度同样可以提高场强差驱动微结构成型。

图5 不同电压对微结构影响Fig.5 Effects of voltages on microstructure

2.3 初始聚合物厚度对微结构成型的影响

由电场诱导微结构成型原理可知，聚合物初始厚度会导致初始态截面的电场强度不同，并且会影响微结构最终达到的形态。模拟的几何尺寸保持不变，电压采用800 V，空气间隙15μm，聚合物初始厚度分别为10、15及20μm，微结构成型的演化过程不变，初始膜厚对结果的影响如图6所示，在相同诱导时间内初始膜厚并没有影响演化过程，但会影响微结构的最终形态，当初始膜厚为10μm时，在一定场强下，微结构波峰接触到了电极微结构，并且底面开始出现了薄膜“消失”现象，聚合物全部聚集在电极结构下端；随着膜厚的增加，聚合物表面既有微结构变化趋势，同时也保留了一定的膜厚。根据电场模曲线图可以看出，膜厚越小，其表面的电场强度越大，膜厚的增加同时也增加了两电极间的距离，导致场强减小。

2.4 相场法与水平集法对比

通过修改几何模型形状和尺寸，保证几何参数和条件参数一致，分别采用相场法和水平集法进行仿真模拟，得到的结果出现了一定差异（见图7）。

通过对比两种算法的仿真结果可以看出，相同时间下，相场法最终达到的结果是凸起电极下整体保持上涨最后与电极接触，而水平集法则形成了中空结构；云图箭头表示速度流向，从箭头方向可以看出，相场法中最底层聚合物由两端向中间流动，而水平集法则相反，由中间流向两侧，导致生长的结构在中间部分产生了差异。而通过场强曲线图可以看出，初始态时相场法中间的场强最大，由于尖端效应，使得相场下凸起电极场强呈现一体态，聚合物整体生长过程中向中间挤压形成了一体态的微结构，随着聚合物的生长慢慢变成了驼峰状场强分布；而水平集法从开始一直是表现为驼峰状，两边生长较快导致中间产生空隙，随着聚合物继续流动，中空结构的位置下移，最终达到稳态，可以看出相场法得到的模拟图更接近实际实验得到的结构。水平集法和相场法计算类似，但表面张力的处理对二者的稳定性产生很大的影响，在COMSOL Multiphysics中存在区别，在处理对表面张力的问题时，相场法在求解时间方面比水平集法更好。

图6 不同初始膜厚对微结构影响Fig.6 Effects of polymer thickness on microstructure

图7 不同算法对微结构影响Fig.7 Effects of algorithms on microstructure

3 结论

本文分析了水平电场下聚合物流变成型诱导机制。在此基础上建立相场数学模型，采用COMSOL Multiphysics软件模拟了结构化电极下影响电场诱导微结构过程的因素，讨论了部分参数（电极宽度、电压、初始膜厚）对微结构成型的影响，得到以下结论：

1）电场强度和作用时间一定时，聚合物微结构生长高度随电极宽度增加而略有增加。

2）增加电压既可以有效提高微结构的生长速度也影响最终微结构的高度。

3）初始膜厚较薄有利于微结构生长。但初始膜厚若低于某一临界点，成型过程会出现“露底”，无法形成连续的膜。此外初始膜厚影响微结构的生长速度，厚度越大，作用在聚合物表面静电力越小，微结构生长越慢。

4）对比水平集法和相场法仿真计算结果，在相同条件下，水平集法得到的模型图案出现中空结构，而相场法则无此现象。原因在于两种算法在处理表面张力以及在处理两相界面时建立的数学模型差异，导致最终结构上的差异。