基于稀疏凸非负矩阵分解的混合数据特征提取与评价研究

周 静，余 超，胡怡宇，杜倩倩

（江汉大学 人工智能学院，湖北 武汉 430056）

0 引言

国外学者较为重视在线课程平台数据资源的研究［1-2]，如美国教育部门建立了“学习分析系统”对学生线上教育数据进行挖掘、模化和案例运用，可以帮助教师了解学生更多、更好、更精确的学习信息；加拿大面向高等教育领域的学生推出“学生成功系统”，帮助教师系统地分析每个学生的在线学习数据，并预测学生的期末考试成绩。国内关于在线课程平台的数据资源的研究大多集中在北京、上海、广州等地，目前已经利用新的数据信息处理手段为在线课程用户提供基本公共在线教育服务，并初步建立在线教育数据挖掘与分析子系统。

综合国内外研究现状，虽然目前已对在线教育数据进行了挖掘和分析，并开发出数据分析平台；但研究基本仅限于在线教育数据，未考虑线下传统课堂数据；同时数据分析基本采用的是传统的机器学习和数据挖掘方法，如回归分类、聚类等方法，难以有效提取出混合学习数据中的群集特征。针对目前的研究现状，本文通过融合传统教学和互联网线上的教育数据构建混合教育数据特征网络，对传统的非负矩阵分解（non-negative matrix factorization，NMF）方法进行改进，提取出混合数据特征网络中影响教育质量的主要群集特征，并基于状态-压力-响应（pressurestate-response，PSR）模型构建教育指标多级评价模型，对个体进行有效分级。

1 数据特征网络构建

数据特征网络的一个重要特征是网络包含少量的高度节点，这些高度节点的“度”很大，说明它们之间以很高的连接概率互联，构成群集［3-4]。学习行为特征节点的“度”越大，表示该行为与其他行为被执行的次数越多，则说明该学习行为特征越重要，这样的学习行为特征之间存在的联系可以看成群集。群集函数特征的差异表明，网络呈现出明显的层次拓扑结构，大多数节点分别依附在若干个节点上，形成若干个小网络，小网络经过选择性的互联形成大网络并产生少数几个中心节点，最后这几个中心节点互联成完整的网络，如图1所示。图1中10个节点分别代表个体的各学习行为特征，由图1可知，10个学习行为特征汇聚形成了4个群集［5-6]，基于4个群集特征构建形成了教育特征网络，该网络中的学习行为特征是指综合学习效果特征指标。

图1 基于群集特征的数据特征网络Fig.1 Data feature network based on cluster feature

2 改进的稀疏CNMF特征提取方法

NMF方法提取数据群集特征的思路是对于任意给定的m×n大小的高维非负矩阵X，压缩分解成两个低维非负矩阵F和U，其中F的维度为m×k，U的维度为n×k，F和U满足X=FUT，其中F为特征矩阵。

凸非负矩阵（conves nonnegative matrix factorization，CNMF）分解是NMF模型的推广，可更有效地抽取混合数据中的群集特征，并通过对特征矩阵的稀疏化减少矩阵分解与特征提取的计算量。CNMF［4，7]模型将矩阵F替换成原始矩阵X的非负凸组合，即F=XV。原始矩阵X维度为m×n，非负凸组合系数矩阵V的维度为n×k，用于表示特征的基矩阵，特征矩阵F的维度为m×k，则可得到CNMF的分解形式为X=XVUT，其中V和U被约束成非负，X没有约束。

基本CNMF的目标函数［8]为

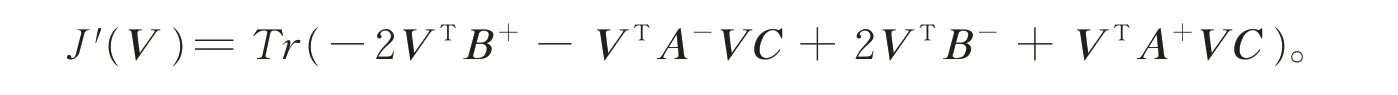
本文提出一个新的目标函数J（V）如（1）式所示，新目标函数比传统的目标函数更简单和易于计算，能够有效提高收敛速度，且对V、U等系数矩阵的优化效果更好，群集特征的识别率更高，

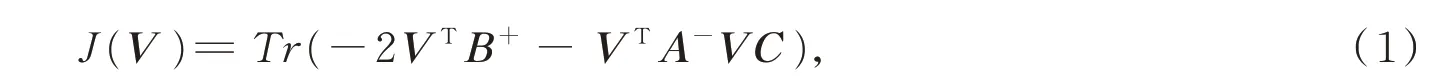
式中，B+=(XTX)+U,A-=(XTX)-,C=UTU。且分别表示矩阵A的正负部分，如（2）式所示，

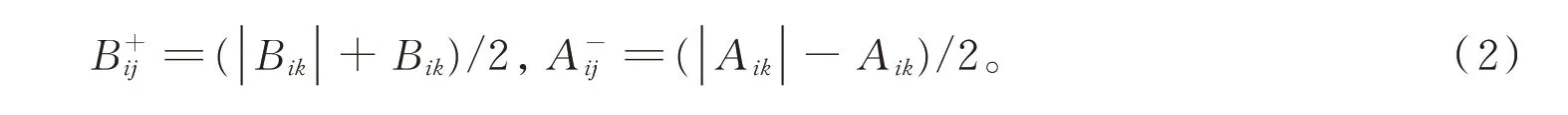
定义一个辅助函数Z(V,V′)，它满足

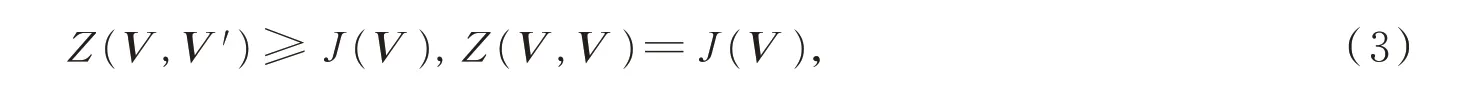
对于任一V和V′，定义

可知：

因此，只要找到符合（3）式的Z(V,V′)，可保证目标函数J(V(t))不增且收敛。

其中

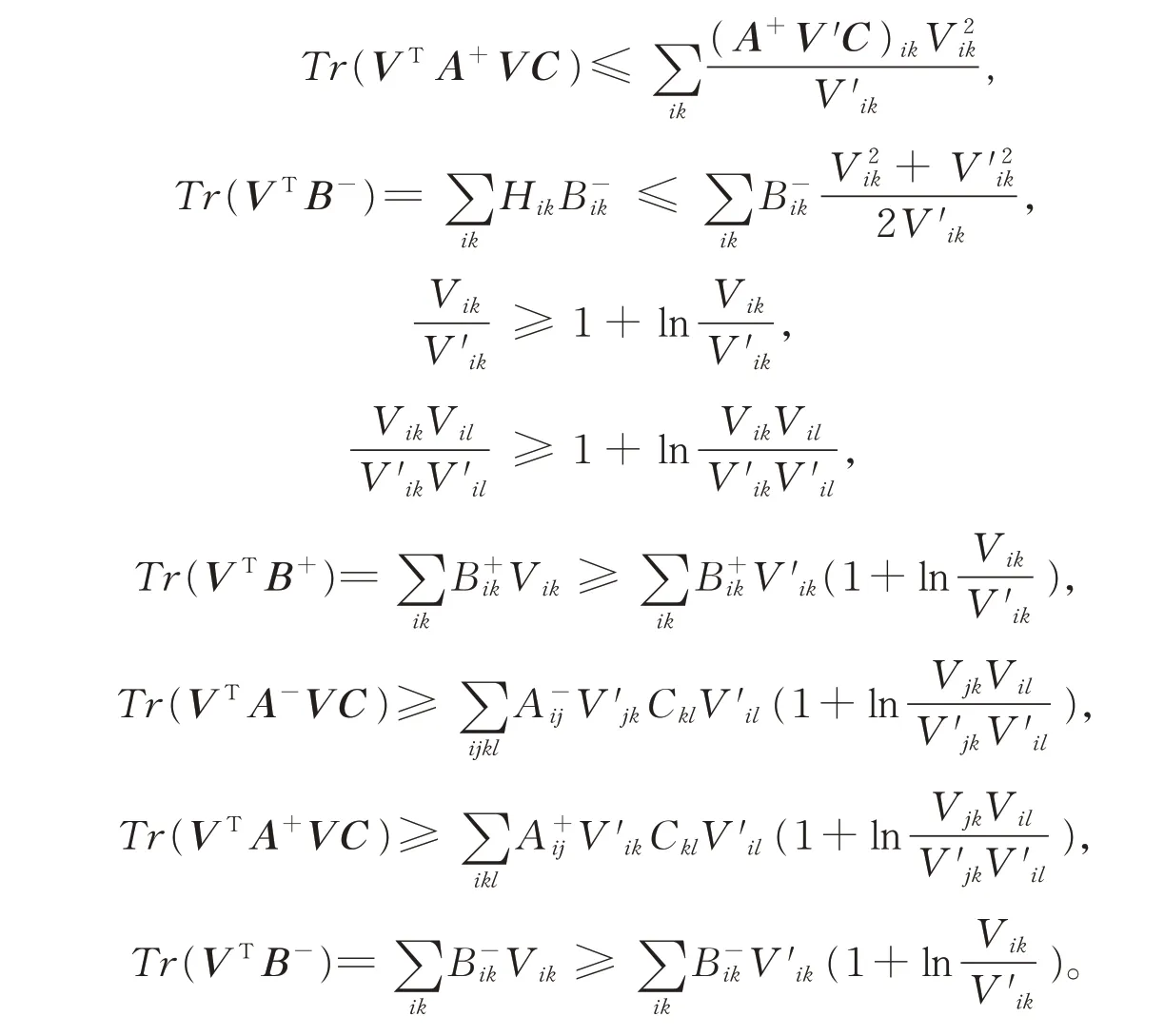
符合（3）式的Z(V,V′)由（5）式定义：

为找到Z(V,V′)的最小值，令其导数为0，则有

Z(V,V′)的最小值由公式（6）计算得到，即可得到使Z取最小值时的V ik，

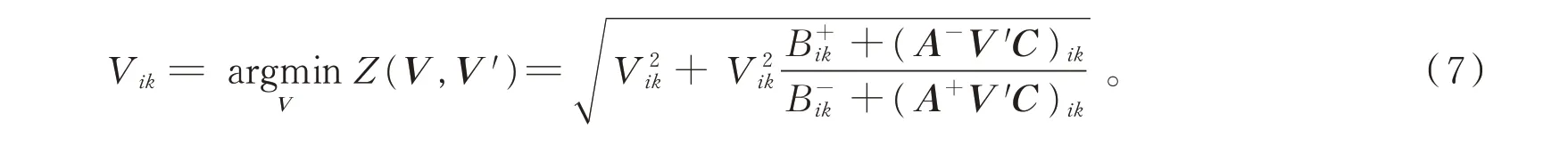
又因为

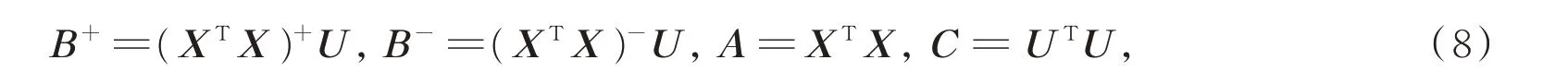
可得到V的迭代规则如（9）式所示：

同理可得到U的迭代公式为

由公式（9）、（10）定义的迭代规则可保证J(V(t))=Z(V(t),V(t))≥Z(V(t+1),V(t))≥J(V(t+1))，使得目标函数J(V(t))是个不增函数且收敛。按照新的迭代规则进行迭代运算时，为消除数据间的冗余信息，需对系数矩阵V加以稀疏条件约束，因此采用阈值判断方法在迭代中对系数矩阵V进行稀疏化约束。即选择一个阈值，对V的每一列分别进行处理，将大于这个阈值的部分保留，其他区域置零，则处理后的矩阵被稀疏化，降低了计算量，同时特征更稀疏可使得提取出的混合数据的群集特征更为集中。

3 基于改进的稀疏CNMF方法提取群集特征

以混合教学数据为例，采集教育个体的学习行为及学习效果等教育特征数据，由教育特征指标数据构成X矩阵。对X进行CNMF分解得到系数矩阵UT，其维度为K×J，即得到了K个群集，UT的第k行第j列的数值记为表示第k个学习行为特征指标隶属于第j个群集的权值系数。值越大，说明第k个学习特征指标隶属于第j个群集的程度越高，因此可找到高度隶属于第j个群集的特征指标。

对江汉大学公共课《计算机基础》教学中的个体行为特征指标数据进行稀疏CNMF分解，得到4个群集，表征各学习特征指标分别隶属于4个群集的系数矩阵U如表1所示。由表1可知，U的第1列的第6、5、1、2行的值较高，说明第6、5、1、2指标隶属于第一个群集的权重较高，即隶属于第一群集的指标按照权重高低分别是：学习进度、任务点、视频观看率、测验成绩。隶属于第二群集的指标按照权重高低分别是：实验成绩、考勤。隶属于第三群集的指标按照权重高低分别是：作业、访问数。隶属第四群集的指标按照权重高低分别是：期末考试成绩、期中考试成绩。

表1 教育特征数据指标的权值系数Tab.1 The weight coefficient of educational char acteristic data index

采用基本CNMF及改进的CNMF方法在特征矩阵维度N取不同值时分别进行群集特征提取，实验结果如图2所示，可知在不同的矩阵维度下改进后的CNMF方法提取群集特征所需时间均小于基本CNMF方法。

图2 群集特征提取时间对比Fig.2 Comparison of cluster feature extraction time

4 教育个体PSR评价体系构建及权值求解

4.1 教育个体PSR评价指标体系构建

基于上述方法提取到的混合教学数据中的群集特征，选取多级指标，采用PSR［9]模型，构建评价层—群集层—特征层的3个层次上的PSR评价指标体系如图3所示。图3中一级指标（评价层）分为所提取到的群集1至群集4的4个二级指标，4个二级指标（群集层）下面又进一步分为10个三级特征指标。

图3 基于稀疏CNMF的教育个体PSR评价指标体系Fig.3 PSR evaluation index system of educational individuals based on sparse CNMF

4.2 基于熵值法求解PSR各指标权重

基于个体质量PSR评价指标体系，考虑到个体的分级不仅由个体的学习特征行为指标决定，还应考虑个体的综合学习效果指标。为了确定各指标对个体分级影响的权值，本文采用熵值法［10]确定指标权值，主要步骤如下：

步骤一对由M个个体、N个指标构建的原始指标数据矩阵X按照（11）式进行标准化，

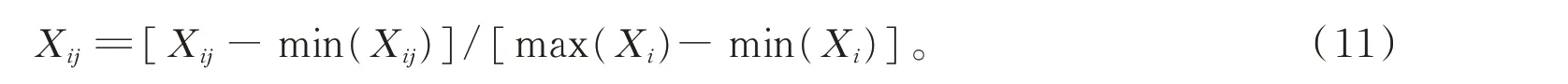
计算第j项指标下第i个个体指标值x ij的权重P ij，

计算第j项指标的熵值E j，

式中，k=1/lnM。

步骤二计算第j项评价指标的差异性系数gj，

步骤三计算第j项评价指标的权重w j，

步骤四计算评价指标权值。基于特征层的指标值，可通过如（16）式所示的加权综合计算方法计算群集层（二级指标）及评价层（一级指标）的指标值，

式中，D j表示上一层指标值；Cj表示下一级指标值；Rj表示Cj相对于D j的权重；N为Cj级指标的数量。

根据上述方法，确定各个指标之间的相对重要程度，可以得到PSR评价指标体系中各指标的权重（见表2）。

5 教育质量综合评价及教育个体分级模型

5.1 教育个体分级理论模型

基于表2中的PSR指标体系中各指标的权重，采用综合加权法计算得到个体的综合评价值，用于衡量个体质量，实现对个体质量的综合评价［9，11]以及个体的分级。

设x i″为第i个一级评价指标所得评价值，x ik′为第i个一级评价指标的第k个二级评价指标所得的评价值，x ikl为第i个一级评价指标，第k个二级评价指标的第l个三级评价指标所得的评价值。将教育质量分级综合评价指标所得的评价值以相应的权重系数来加权，其加权和作为教育质量的综合评价值y，教育质量分级综合评价模型为

表2 PSR评价指标体系中各指标的权重值Tab.2 The weight value of each index in the PSR evaluation index system

5.2 分级阶梯模型建立

由式（17）所计算得到的教育个体质量综合评价值越大，则说明教育质量级别越高，个体质量越好，级别数越靠前，反之亦然。因此可建立分级阶梯模型如式（18）所示，用于确定教育个体质量的级别数，

由（17）式和（18）式可求得各个体样本的综合评价指标值与分级值，并给出200个个体样本分属于10级的分布曲线（见图4），图4横轴表示级别数，纵轴表示学生人数。图4同时给出了依据学生期末考试成绩得到的理想分级值的分布曲线。

图4 个体分级分布图Fig.4 Individual classification distribution map

由图4可知，本文所提出的评价指标体系对学生进行分级评价的结果与学生个体期末考试成绩的理想分级结果基本一致，证明了本文所提出的特征提取方法及评价分级模型的有效性。

6 结语

本文针对线上和线下混合教学中所获取的教育特征数据，构建基于群集的教育特征网络；采用改进迭代规则的稀疏凸非负矩阵分解特征提取算法对教育特征网络数据进行降维，提取影响教育特征网络的群集特征。根据该反映个体质量的群集特征的权值大小，可分析得到个体质量的核心指标；同时，通过选取多级特征指标构建了混合教学模式下个体质量的PSR评价指标体系；采用综合评价法构建个体质量综合评价模型和分级模型，并对该课程混合教学中的教育个体进行了有效分级，分级结果分布与学生个体期末考试成绩的理想分级结果基本一致，证明了本文算法的有效性。