First-principles investigation of the valley and electrical properties of carbon-doped α-graphyne-like BN sheet*
2021-05-24BoChen陈波XiangQianLi李向前LinXue薛林YanHan韩燕ZhiYang杨致andLongLongZhang张龙龙
Bo Chen(陈波), Xiang-Qian Li(李向前), Lin Xue(薛林),Yan Han(韩燕), Zhi Yang(杨致), and Long-Long Zhang(张龙龙)
College of Physics and Optoelectronics,Taiyuan University of Technology,Taiyuan 030024,China
Keywords: first-principles calculations, α-graphyne like structures, valleytronic materials, wide band gap semiconductors
1. Introduction
Valleytronics, a new field beyond electronics and spintronics, are based on exploiting and manipulating the electron valley degree of freedom, which is the energy extrema in momentum space.[1,2]The most representative valleytronic materials are monolayers of semiconducting transition metal dichalcogenides MX2(M =Mo, W; X =S, Se), which have two degenerate yet inequivalent valleys at the corners of their hexagonal Brillouin zones (the K and K′points). And these two inequivalent valleys are connected by time-reversal symmetry. Due to the lack of the inversion symmetry, carriers in these two inequivalent valleys are subject to opposite Berry curvatures,[3]which are gauge-independent pseudovectors that reflect the handedness and geometries of Bloch waves and act like effective magnetic fields in momentum space.[4–6]The opposite Berry curvatures, direct band gap,and angular momentum of the atomic orbitals together contribute to the different optical selection rules for the two valleys, thus permitting the generation of valley polarization by controlling the helicity of light.[7–9]However, the low carrier mobilities (about 200 cm2·V−1·s−1for MoS2monolayer) and direct-to-indirect band gap transition induced by strain in MX2monolayers restrict their practical applications in valleytronics.[10,11]In addition,the restored inversion symmetry in MX2bilayers makes Berry curvature zero at any point in the entire Brillouin zone, which prohibits valley polarization in MX2bilayers via the circularly polarized light. Therefore new two-dimensional(2D)valleytronic materials with moderate and robust direct band gaps,high carrier mobilities,and inversion asymmetry independent of layer number are remained to be found.
Owing to the inversion asymmetry and direct band gap of about 6.0 eV,[12]honeycomb boron nitride (h-BN) monolayer is an ideal material to realize valleytronics in the ultraviolet region, but its carrier mobility at room temperature is as low as 0.01 cm2·V−1·s−1.[13]The carrier mobility of h-BN monolayer may be enhanced by carbon doping,[14]along with a tunable band gap from deep ultraviolet to far-infrared spectra,depending on the carbon doping concentration.[15]Like h-BN monolayer,the inversion asymmetric boron nitride analog of α-graphyne (labeled as α-BNyne) monolayer has a direct band gap of 5.428 eV and a low electron mobility of about 132.04 cm2·V−1·s−1, as shown in Figs. A1, A2 and Table A1 in supplement material. So we wonder if it is possible that carbon doping could increase the carrier mobilities of α-BNyne while maintaining its direct band gap nature and inversion asymmetry,which is worthy of exploration. In this paper,we predict two valleytronic materials,B3C2N3and BC6N,through ab initio density functional theory(DFT)calculations.We show that both B3C2N3and BC6N monolayers are energetically more stable than α-BNyne, and have direct band gaps of 3.143 eV and 2.683 eV,respectively. The direct band gap feature is robust against the biaxial strain. Further calculations demonstrate that B3C2N3and BC6N monolayers exhibit relatively high carrier mobilities,and inversion asymmetry is reserved in the energetically most favorable B3C2N3and BC6N bilayers.Finally,the capacity of BC6N monolayer to be a photocatalyst for water splitting and the separation of photogenerated electrons and holes in B3C2N3-BC6N van der Waals heterostructure are revealed.
2. Computational methods
Our DFT calculations are performed by using Vienna ab initio simulation package (VASP).[16]Ion–electron interaction is described by the projector augmented wave(PAW) potentials.[17,18]Exchange–correlation between electrons is treated using the generalized gradient approximation(GGA) in Perdew–Burke–Ernzerhof (PBE) form.[19]Threedimensional periodic boundary conditions are applied, and a vacuum region of 30 ˚A is incorporated to avoid interactions between neighboring layers. Geometry optimization is done using the conjugated gradient method[20]with a 3×3 supercell (72 atoms) to avoid possible artifacts of single cell calculations.[21]The energy cutoff of the plane waves is set to 700 eV, with an energy precision of 10−6eV. A 3×3×1 Γ centered Monkhorst–Pack grid is used to sample the Brillouin zone (the convergence tests of energy cutoff and number of k-points are shown in Fig.B1 in supplement material).The atomic positions are fully relaxed until the force on each atom is less than 10−2eV/˚A.Considering that the GGA usually underestimates the band gap, Heyd–Scuseria–Ernzerhof(HSE06) hybrid functional[22]is adopted to correct the band structures and optical absorption coefficients. Phonon spectra are calculated using a 3×3 supercell approach within the Phonopy code[23]interfaced with density functional perturbation theory[24]implemented in VASP. Ab initio molecular dynamics (AIMD) simulations are carried out at room temperature by using canonical ensemble (NVT) with a 4×4 supercell (128 atoms). Each simulation lasts for 6 ps with a time step of 1.0 fs, and the temperature is controlled by applying the Nos´e–Hoover algorithm.[25,26]For the B3C2N3and BC6N bilayers and vertical heterostructures formed by stacking B3C2N3and BC6N monolayers, van der Waals interaction is included by employing DFT-D3 method.[27,28]The maximally localized Wannier functions are constructed by Wannier90 code,[29]and the Berry curvatures are calculated through WannierTools package.[30]VASPKIT program is used for data post-processing.[31]
3. Results and discussion
3.1. Structures and stabilities
Like carbon-doped γ-BNyne,[32]two carbon-doped α-BNyne structures are studied here. As shown in Fig. 1,B3C2N3is composed of hexagonal carbon rings linked by BN chains, while BC6N is composed of BN hexagons connected by carbon chains. There are eight atoms in one primitive unit cell. Atoms at the corners of the hexagonal honeycomb are sp2-hybridized, because the angle of two neighboring bonds of the atoms is 120°;while atoms at the sides of the hexagonal lattice are sp-hybridized, because they are located in a strict straight line with the atoms at the corners. The lattice constants and bond lengths of the optimized geometric structures for B3C2N3and BC6N monolayers are summarized in Table 1,with α-BNyne included as a control sample(see Fig.A1(a)in supplement material).

Fig. 1. Top view of B3C2N3 and BC6N monolayers. The dashed line delineates the primitive unit cell.

Table 1. Lattice constant a0, bond lengths l1, l2, and l3, cohesive energy Ecoh, calculated elastic constants Cij, Young’s modulus Y, and Poisson’s ratio ν for B3C2N3 and BC6N monolayers. α-BNyne(B4N4)is included for comparison.
Cohesive energies are calculated to evaluate the energetic stabilities of B3C2N3and BC6N monolayers using the expression Ecoh=(mEB+nEC+tEN−Etot)/(m+n+t),where EB/EC/ENand Etotare the total energies of an isolated B/C/N atom and a primitive unit cell,respectively. m/n/t is the number of B/C/N atoms in the primitive unit cell. As displayed in Table 1,the cohesive energies of B3C2N3and BC6N monolayers are higher than that of α-BNyne, indicating that B3C2N3and BC6N monolayers are substantially more stable than α-BNyne. The mechanical stabilities of B3C2N3and BC6N monolayers are assessed on the basis of Born criteria.[33]Due to the added relation C66=(C11−C12)/2, there are five independent elastic constants in the hexagonal crystal system,and the necessary and sufficient conditions for elastic stability can be derived by calculating the eigenvalues of the stiffness matrix. For mechanically stable 2D hexagonal materials,the following conditions must be met: C11>|C12|, 2C213<C33×(C11+C12),C44>0. According to our results shown in Table 1,the computed elastic constants satisfy the Born criteria,which indicates that both the B3C2N3and BC6N monolayers are mechanically stable. Furthermore,2D Young’s modulus(in-plane stiffness)Y and Poisson’s ratio ν can be deduced as Y =(C211−C212)/C11and ν =C12/C11.[34]The calculated Young’s modulus for graphene is 338.609 N/m, which is in accordance with the experimental result of 340 N/m.[35]This supports the reliability of the procedure we employed. As reported in Table 1, it seems that the Young’s modulus and Poisson’s ratio of α-BNyne are more affected when doping carbon atoms at sp2-positions,which may be attributed to the one more bond of sp2-site compared to sp-site. Similar to α-BNyne,[36]B3C2N3and BC6N monolayers are also soft materials and may have a large deformation under a low stress.The dynamic stabilities of B3C2N3and BC6N monolayers are evaluated by calculating the phonon spectra displayed in Figs. 2(a) and 2(b). Because of the neglectable contribution of imaginary phonon frequencies in the entire Brillouin zone,B3C2N3and BC6N monolayers are confirmed to be dynamically stable. Additionally, AIMD simulations at room temperature are performed to investigate the thermal stability of B3C2N3and BC6N monolayers. As seen from Figs.2(c)and 2(d), structural integrity could be maintained well at the end of the simulation, demonstrating the promising thermal stability of B3C2N3and BC6N monolayers. Atoms of B3C2N3or BC6N monolayer at room temperature are not on the same plane, which is a common characteristic for 2D materials to resist the thermal perturbation via fluctuation.

Fig. 2. Phonon dispersions of (a) B3C2N3 and (b) BC6N monolayers,as well as snapshots for the final configurations of(c)B3C2N3 and(d)BC6N monolayers at room temperature.
3.2. Electronic and valley-related physical properties of B3C2N3 and BC6N monolayers
After confirming the excellent stabilities of B3C2N3and BC6N monolayers, we wonder whether they have a sizeable direct band gap just like α-BNyne. As exhibited in Figs.3(a)and 3(b), both B3C2N3and BC6N monolayers are nonmagnetic semiconductors with direct band gaps of 3.143 eV and 2.683 eV, respectively, calculated at the HSE06 level of theory. The valence band maximum(VBM)and conduction band minimum(CBM)of B3C2N3/BC6N monolayer are located at the K point in the Brillouin zone. For B3C2N3monolayer,the partial density of states(PDOS)shows that the valence bands near the Fermi level are predominantly composed of pzorbitals of N atoms and the C atoms surrounded by B atoms,while the conduction bands close to the Fermi level are mainly consisted of pzorbitals of B atoms and the C atoms surrounded by N atoms. This is further confirmed by the isosurfaces of charge densities of VBM and CBM as illustrated in Fig. 3(c). For BC6N monolayer, PDOS and isosurfaces of charge densities of VBM and CBM (Fig. 3(d)) reveal that the valence bands around the Fermi level are predominantly composed of pzorbitals of N atoms and C atoms at the carbon chains,while the conduction bands in the vicinity of the Fermi level are mainly consisted of pzorbitals of B atoms and the C atoms that surround the N atoms. So B3C2N3and BC6N monolayers are two-dimensional direct wide band gap semiconductors. The larger band gap of B3C2N3monolayer compared to that of BC6N monolayer may due to the larger electronegativity difference between B and N in B3C2N3than that between B and C or between N and C in BC6N.[37,38]Interestingly,the charge density of VBM/CBM of B3C2N3monolayer looks like that of CBM/VBM of BC6N monolayer. This possibly leads to opposite responses of band gaps to biaxial strain,which we will discuss later.
Similar to semiconducting MX2monolayers, the timereversal symmetry and the inversion asymmetry make B3C2N3/BC6N monolayer have two energy-degenerate but inequivalent valleys at the corners of the first Brillouin zone,namely, the K and K′valleys, and these two valleys have opposite Berry curvatures. According to Kubo formula,[39–41]Berry curvature Ω(k)can be written as

where |ψnk〉 is the Bloch function with eigenvalue En, fnis the Fermi–Dirac distribution function, and vx(y)are the velocity operators. The Berry curvatures of the occupied states for B3C2N3and BC6N monolayers are obtained through constructing the maximally localized Wannier functions, as seen in Fig.4(a).

Fig. 3. Band structures and PDOSs obtained within the HSE06 scheme for (a) B3C2N3 and (b) BC6N monolayers, the VBM is set to 0 eV.Charge densities of VBM and CBM states for(c)B3C2N3 and(d)BC6N monolayers.
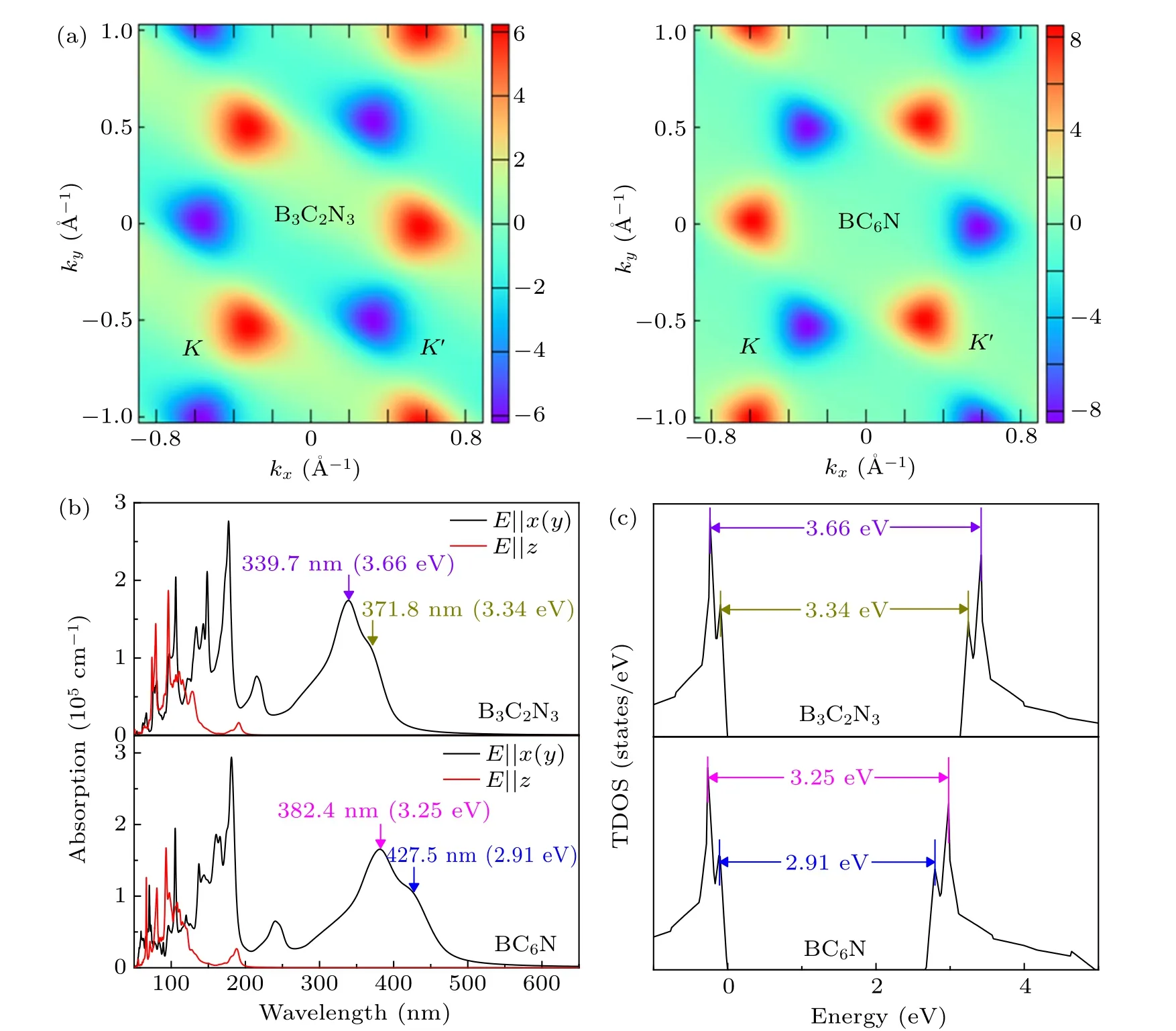
Fig. 4. (a) Berry curvatures, (b) absorption coefficients, and (c) TDOSs of B3C2N3 and BC6N monolayers, where the absorption coefficients and TDOSs are calculated with the HSE06 hybrid functional.
Obviously, the Berry curvatures at K and K′valleys exhibit obvious peaks but with opposite signs, and the distribution of Berry curvatures shows C3vsymmetry. So although the electrons in the neighboring valleys have the same energy,they can be distinguished by their opposite Berry curvatures.Meanwhile, for the incident light with the electric field (E)polarized along the x, y (E⊥z), and z (E ‖z) directions, absorption coefficients α(ω)can be calculated according to the formula:[42]

where ε1(ω) and iε2(ω) are the real and imaginary parts of the dielectric function ε(ω) (ε(ω) = ε1(ω)+iε2(ω)), c is the magnitude of light velocity in vacuum, and ω is the circular frequency of the incident light. As depicted in Fig.4(b),we find that the absorption coefficients are the same for polarization along the x and y directions, which may indicate the isotropic in-plane optical properties. Both the B3C2N3and BC6N monolayers have two high in-plane absorption peaks in the 300–450 nm region, which may be caused by the transitions between the corresponding peaks in the total density of states (TDOS) displayed in Fig. 4(c), as the transition probability of electrons is proportional to the TDOS.[43]Hence,the direct band gaps,valley-contrasting Berry curvatures,together with the large absorption coefficients make valley polarization in B3C2N3and BC6N monolayers achievable via valleyselective circular dichroism.[9]
For B3C2N3and BC6N monolayers utilized in valleytronics, two requirements must be met. One is that B3C2N3and BC6N monolayers should have relatively high carrier mobilities. The other is that the direct band gap nature can be maintained under strain, because B3C2N3and BC6N monolayers are soft materials and may have a large deformation under a low stress,as mentioned above. The carrier mobilities of electrons and holes for B3C2N3and BC6N monolayers are calculated based on the deformation potential theory,[44]which has been extensively used to evaluate the carrier mobilities of 2D materials.[45,46]For inorganic semiconductors, the coherent wavelength of thermally activated electrons or holes is comparable to the wavelength of acoustic phonon and is much longer than the typical bond length,so the scattering of a thermal electron or hole is dominated by the electron–acoustic phonon coupling. On the basis of effective mass approximation,the carrier mobility in 2D materials can be expressed as

where e,kB,T, ¯h,and m*are the electron charge,Boltzmann constant,temperature,reduced Planck constant,and carrier effective mass,respectively. C2Dis the elastic modulus defined as C2D=(∂2E2D/∂δ2)/S0,in which E2Dis the total energy of the system, S0represents the area of the optimized structure.δ is the applied biaxial strain and is defined by (a −a0)/a0,here a0and a are the optimized lattice constant and the lattice length along the strain direction, respectively. Negative and positive values of strain stand for the compression and elongation, respectively. Edis the deformation potential constant denoting the shift of the band edges (CBM for electrons and VBM for holes)induced by the strain. For B3C2N3and BC6N monolayers,the changes of total energies and band edges with biaxial strain are illustrated in Fig.C1 in supplement material,and the obtained C2D, Ed, m*, µ at 300 K for B3C2N3and BC6N monolayers are compiled in Table 2. It should be noted that the shift of the VBM for B3C2N3monolayer is small and is not linear with the biaxial strain,as shown in Fig.C1(a).The reason is unclear now, which needs further research. Compared to the electron mobility of 132.04 cm2·V−1·s−1and hole mobility of 1527.16 cm2·V−1·s−1for α-BNyne, doping carbon atoms at the corner could increase the electron mobility by about four times,while doping carbon atoms at the side of hexagonal lattice could greatly enhance the electron mobility and maintain the hole mobility. So doping carbon atoms in α-BNyne would increase the carrier mobilities. B3C2N3and BC6N monolayers exhibit relatively high carrier mobilities.
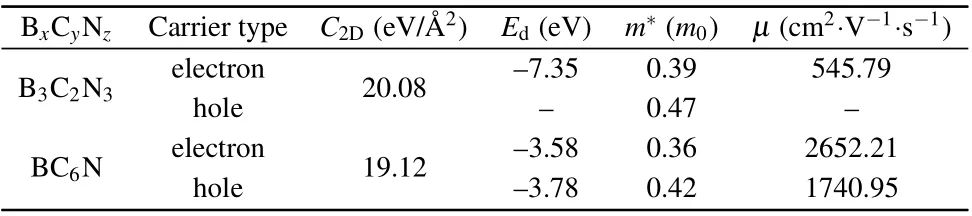
Table 2. Calculated elastic modulus C2D, deformation potential constant Ed, effective mass m*, carrier mobility µ at 300 K for B3C2N3 and BC6N monolayers. m0 is the mass of free electron. Ed and m* are obtained by the HSE06 method.

Fig.5.Electron localization function maps for h-BN,α-BNyne(B4N4),B3C2N3,and BC6N.
Why carbon doping can increase the electron mobility of α-BNyne? For h-BN, the large electronegativity difference between B and N makes the B–N bond ionic.[47,48]So electrons are bound to the N atoms, as demonstrated by the electron localization function(ELF)map of h-BN shown in Fig.5.This causes the low electron mobility and large band gap in h-BN. Like h-BN, electrons are also bound to the N atoms in α-BNyne, hence its electron mobility is low and its band gap is large. Furthermore, from ELF map of α-BNyne we can find that the sp-hybridized N atoms at the sides of hexagonal lattice have stronger ionic nature compared to the sp2-hybridized N atoms at the corners of hexagonal honeycomb.When doping carbon atoms into α-BNyne, its intermediate electronegativity between those of B and N atoms makes the B–C and C–N bonds have stronger covalent nature and weaker ionic properties than the B–N bond, as verified by the ELF maps of B3C2N3and BC6N monolayers in Fig. 5. So electrons in B3C2N3and BC6N monolayers are less bound and more mobile compared with the electrons in α-BNyne. More significantly, there are no sp-hybridized N atoms in BC6N monolayer,thus it has high electron mobility over the B3C2N3monolayer.
Interestingly, from Table 2 and Fig. C1 we can find that in B3C2N3monolayer,the shift of CBM is quit dependent on the biaxial strain, contrary to the basically independence of VBM on biaxial strain. But in BC6N monolayer,the absolute value of Edfor VBM is little larger than that for CBM.So with the increase of biaxial strain,band gap for B3C2N3monolayer should decrease while band gap for BC6N monolayer should increase, and the rangeability of band gap of B3C2N3monolayer is larger than that of band gap of BC6N monolayer. To prove our deduction, biaxial strain dependent band structures and band gaps of B3C2N3and BC6N monolayers are calculated by using the HSE06 functional,as presented in Figs.C2,C3 and 6. It can be seen that the locations of VBM and CBM are at K point in the Brillouin zone and do not move within a strain range from −2%to 2%, indicating that the direct band gap feature of B3C2N3and BC6N monolayers is robust against the biaxial strain. Changes of band gaps for B3C2N3and BC6N monolayers are opposite and agree with our inference.We attribute this to the fact that B3C2N3and BC6N monolayers have inverse charge density distributions at the band edges,which may result in the opposite responses of the band gaps to biaxial strain.
In addition, band edges of B3C2N3and BC6N monolayers can straddle the redox potentials of water (at pH=0, the standard oxidation potential of H2O/O2is −5.67 eV, and reduction potential of H+/H2is −4.44 eV.Vacuum level is set to zero for reference),[49]but the band gap of B3C2N3monolayer is too large for efficient solar energy absorption. So BC6N monolayer might be a promising candidate photocatalyst for practical applications in visible-light-driven water splitting.

Fig.6. Band gaps as a function of biaxial strain for B3C2N3 and BC6N monolayers.
3.3. Bilayers and heterostructures
Since B3C2N3and BC6N monolayers are valleytronic materials, we address the question of whether B3C2N3and BC6N bilayers can also be utilized in valleytronics, or not.Like α-BNyne bilayer,[50]five different high symmetry stacking configurations are proposed and investigated for B3C2N3and BC6N bilayers,as shown in Fig.7.

Fig.7. Top and side views for the different stacking configurations of B3C2N3 and BC6N bilayers.




Fig. 8. (a)/(b) Band structure (HSE06) and (c)/(d) Berry curvature for B3C2N3/BC6N bilayer with AB-III configuration.



Fig.9. Top and side views for the B3C2N3–BC6N van der Waals heterostructures in six different stacking orders.

Fig. 10. (a) Band structure and charge densities of (b) VBM and(c) CBM states for AB-I stacking B3C2N3-BC6N van der Waals heterostructure.
4. Conclusions
Using first-principles calculations, we demonstrate that carbon doping can increase the carrier mobilities of α-BNyne while maintain its direct band gap nature and inversion asymmetry,which make the two carbon-doped α-BNyne structures,namely, the B3C2N3and BC6N monolayers, potential valleytronic materials. More importantly, unlike the MoS2bilayer, optical pumping with circularly polarized light might achieve valley polarization in the energetically most favorable B3C2N3and BC6N bilayers. Besides, the promising photocatalytic activity of BC6N monolayer for efficient solar water splitting and the type-II energy band alignment between B3C2N3and BC6N monolayers are revealed.
We should note that except for α-BNyne, β-, γ-, and 6,6,12-BNyne are all direct wide band gap semiconductors with inversion asymmetry,[51]and the valley properties are affected by temperature and magnetic field.[52,53]So do these materials have relatively high carrier mobilities? If not, can carbon doping increase their carrier mobilities and make them suitable for applications in valleytronics? What is the influence of temperature and magnetic field on the valley properties of B3C2N3and BC6N monolayers? Can valley splitting be realized in the heterostructure formed by stacking B3C2N3/BC6N monolayer with a ferromagnetic material? These are worthy of exploration. Further researches are in progress.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Process modeling gas atomization of close-coupled ring-hole nozzle for 316L stainless steel powder production*
- A 532 nm molecular iodine optical frequency standard based on modulation transfer spectroscopy*
- High-throughput identification of one-dimensional atomic wires and first principles calculations of their electronic states*
- Effect of tellurium(Te4+)irradiation on microstructure and associated irradiation-induced hardening*
- Effect of helium concentration on irradiation damage of Fe-ion irradiated SIMP steel at 300 °C and 450 °C*
- Optical spectroscopy study of damage evolution in 6H-SiC by H+2 implantation*
