在幺正规范(ξ→∞)下推导t→cγ振幅
2021-05-24柳国丽别素雅
柳国丽,别素雅
(郑州大学 物理学院 河南 郑州 450001)
0 引言
当单圈构成的图形没有树图贡献时,其所有图形贡献的发散项全部相加的结果为零。但在计算内线为荷电规范玻色子和费米子组成的圈图时,却不能满足所有发散项相加结果为零这一要求。利用波函数的幺正性也能在计算中消去发散项[1]。下面从幺正性消去发散项的方法来计算t→cγ过程。
1 单圈图μ→eγ发散项不能相消
1.1 μ→eγ费曼图
图1中的费曼规则为:

图1 μ→eγ 费曼图
(1)
(2)
γφW∶-igμν。
(3)
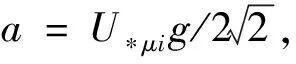
本文耦合是模型无关的,取新物理中的一般形式,所以发散性不依赖于具体模型。因为没有树图贡献,所有的发散项加起来应该为零。为简单起见,将上面这些耦合写成更一般的形式:
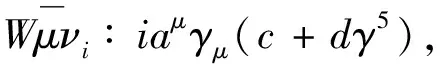
(4)
(5)
其中c=d=±1,暂取为自由参数。
1.2 各项展开计算
为了更好地利用计算机圈图程序计算,采用费曼规范,取ξ=1。W粒子和φ粒子的传播子为:
(6)
(7)
γφW的耦合对应gμν项,没有发散项,而考虑的是发散项的相消问题,所以图1(d)和(h)项暂且不考虑。
1.2.1图1(a)的计算
γρq1ργλkλγμ·aa+γμγρkργλq3λ·aa],
(8)
其中:f1=c2+d2;f2=2cd;f3=c2-d2;aa=f1+f2γ5;q1=p3-2p4;q2=p3+p4;q3=p4-2p3;
iMa中前3项b1(-4kμγρkρaa+2dkμγρkρ·aa+2k2γμ·aa)包含有发散项,按三点函数[2-3]展开。由
可以看出C2(4)含Δ/4发散因子(B0含一个Δ发散因子)。b1(-4kμγρkρ·aa+2dkμγρkρ·aa+2k2γμ·aa)展开为
(9)
1.2.2计算图1(b)
(10)

(11)
1.2.3计算图1(c)
d=4时有发散项
c1[-4f3(mνi/m4)γμB0]→-4f3(mνi/m4)γμΔc1。
(12)
1.2.4图1(a)~(c)中的发散项之和为
(13)
1.2.5图1(e): 2条鬼粒子内线
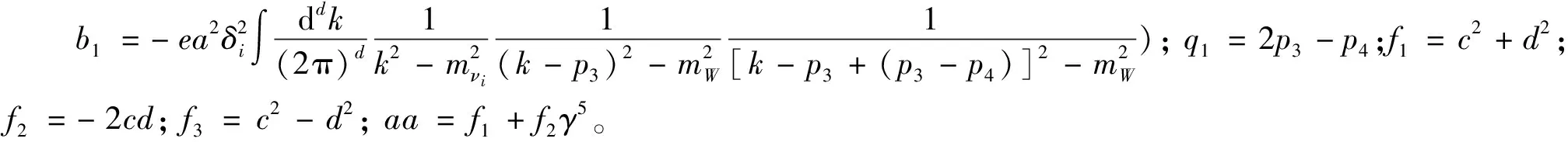
1.2.6计算图1(f)
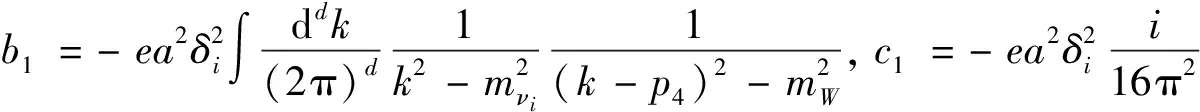
c1[γμ·aa/2+f3mνi/m4γμ]→(γμ/2·aa+f3mνi/m4γμ)Δc1。
(14)
1.2.7计算图1(g)
上式中发散项为
c1[-f3mνi/m4γμB0]→-f3mνi/m4γμΔc1。
(15)
1.3 图1(e)~(g)发散项之和为零
c1Δ[-·γμ·aa/2+γμ·aa/2+f3mνi/m4γμ-f3mνi/m4γμ]=0。
1.4 所有单圈发散项相加不为零
所有发散项相加不为零。内线上标量粒子的发散没有问题(不管是不是鬼粒子)。在下面t→cγ计算中,将根据文献[1]中关于此类过程洛伦兹结构的讨论,运用Ward恒等式[4]和CKM矩阵元的幺正性[5]舍弃发散项,计算t→cγ过程的振幅。
2 顶夸克衰变t→cγ
在费曼规范(ξ=1)下,计算时会不可避免地出现发散项。由于在幺正规范(ξ=∞)下,不会出现Goldstone粒子,故可利用CKM矩阵元的幺正性和Ward恒等式直接计算出最终结果。下面给出t→cγ的详细计算过程。
2.1 振幅一般形式
t→cγ振幅可写为
(16)
(17)
由电磁场的规范不变性,
(18)
则有
-mc(C+Dγ5)+mt(C-Dγ5)+q2(E+Fγ5)=0,q2=0,C=D=0。
(19)

(20)
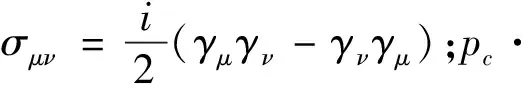
2.2 费曼规则
各个顶点为
(21)
(22)
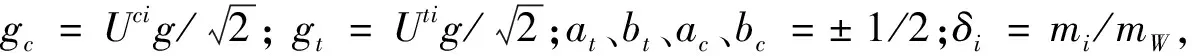
在幺正规范ξ=∞下的传播子如下。
1)对于所有的质量不为零的规范玻色子:
2.3 费曼规范下的费曼图t→cγ及图2(a)的振幅
图(2)给出了t→cγ费曼图。虽然其中有鬼粒子内线图,但在幺正规范下,鬼粒子将消失,故本文不予考虑,所以图2(d)~(j)的贡献都为零。图2(b)、(c)的振幅正比于γμ,由前面讨论可知,此类贡献可忽略。所以图(1)只剩下图2(a)和图2(i)有贡献。由文献[1]可知图2(a)中,
(23)
下面将着重介绍图2(i)的计算。
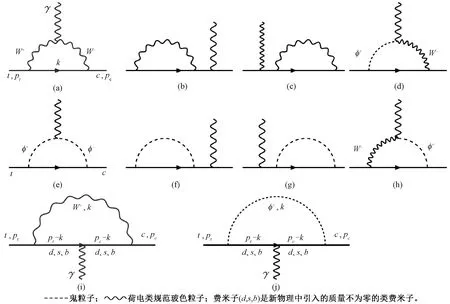
图2 t→cγ 费曼图
2.4 计算图2(i)的振幅Mi
(24)
下面将分别计算式(24)的分子和分母部分。

(25)
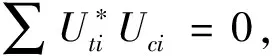
(26)
故可得
(27)
(28)
(29)
(30)

(31)
(32)



由(24)式可知Δρλ为
其中:k1=pt-k;k2=pc-k;f1=(atac+btbc);f2=(acat-bcbt);f3=-(acbt+bcat);f4=(acbt-bcat);a1=f1+f3γ5;a2=f2+f4γ5(a1、a2只是形式上简化,因其含有γ5因子,故一定写在式子的最左边)。令
(33)
(34)
将k、k1、k2代换为l和pt、pc,即
l+(xpt+ypc)=l+q,k1=-l+q1=k′1,k2=-l+q2=k′2,
其中:q=xpt+ypc;q1=(1-x)pt-ypc=pt-q;q2=(1-y)pc-xpt=pc-q,
则S1,S2变为S′1,S′2(d维)
(35)
S11=4a2mi-4a2xmi-4a2ymi-2a2(4-d)mi+a2x(4-d)mi+a2y(4-d)mi+2a1xmt-2a1x2mt-
2a1xymt+a1(4-d)mt-2a1x(4-d)mt+a1x2(4-d)mt-a1y(4-d)mt+a1xy(4-d)mt;
(36)
S12与结果无关,故略。在结合分母以后的积分中,lμLν的积分等同于1/4l2gμν,故式(36)令二者相等。即
(37)
S2的计算与之大致相同,但更为复杂,用Mathematica软件给出结果,
这里也略去了包含γμ的项,其中:

由S1、S2可得

(38)
2.4.3综合推导Mi
将式(25)、(26)、(27)和(37)代入式(24)有
(39)
根据电磁流守恒有qμ·μ=0,且对z(z=1-x-y)可积分得出。其中由于没有出现1/项,故S11、S21、S22中无穷小项可忽略不计。先将S11、S21、S22表示成x的多项式:
S11=4a2mi-4a2miy+(-4a2mi+2a1mt-2a1mty)x+(-2a1mt)x2=ax2+bx+c;
(40)
(41)
S21=(-3a2mi-3a1mt)x+3a2mi-4a2miy=gx+h,
(42)
其中:
(43)
将式(30)中Δ进行变化,
(44)
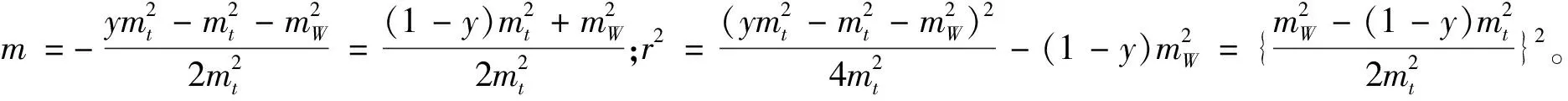
积分中,x范围为(0,1),-m≤t≤1-m,且m-r=1-y。将式(40)、(41)、(42)、(44)代入式(39)中,得
(45)
si(i=1,…,8)分别为:
(46)
(45)式计算中用到含有1/(t2-r2)项的积分形式,这里不再赘述。
关于费曼参数x、y的初等函数积分,可用数值积分直接给出结果。
(47)

(48)
这里的计算结果与图1(a)的振幅相比要复杂得多,这是因为:1)本文考虑的耦合是全部洛伦兹结构,而在图1(a)计算中只考虑了矢量玻色子与费米子的左手耦合,这样的考虑会增加至少4倍的工作量。2)由于内线夸克的质量也出现在分子中,增加了计算的难度,而只考虑左手结构则可直接约去内线费米子质量。3)由于内线有两个费米子,这大大增加和丰富了分子中γ项的结构和项数。
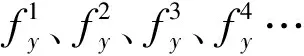
最后,矢量玻色子可以很重,如新的规范群破缺产生的规范玻色子WH,目前精确实验已将其推到比较高的质量范围[9]。
3 总结
本文首先说明了在内线为矢量传播子的情况下,过程μ→eγ和t→cV(V=Z,γ,g)的单圈图不能借助于计算程序有效消除。接着给出了在Ward恒等式和幺正性限制下的t→cγ洛伦兹结构,并对之进行计算,最后比较了与图1(a)计算的不同之处。
