基于可拓关联度比的三支决策模型及应用
2021-05-24杨亚锋李丽红
李 敏,杨亚锋,雷 宇,李丽红
(1.华北理工大学 理学院 河北 唐山 063210;2.河北省数据科学与应用重点实验室 河北 唐山 063210;3.唐山市数据科学重点实验室 河北 唐山 063210;4.华北理工大学 电气工程学院 河北 唐山 063210)
0 引言
三支决策是在粗糙集的基础上提出的,是一种处理不确定性决策的数学方法,姚一豫等[1]基于各个领域中三支决策的共性及特征,提出三支决策理论框架。自提出以来,三支决策备受学者关注,从不同角度进行深入研究。针对勾股模糊三支决策概率阈值难以确定的问题,文献[2-3]给出概率阈值确定方法和基于勾股模糊集评价的三支决策方法,同时结合直觉模糊集理论提出一种基于直觉模糊相似度的三支决策方法;薛占熬等[4]通过研究粒度重要度的构造方法,提出一种新的基于粒度重要度的三支决策模型将证据理论引入三支决策中,分析延迟信任区间可能包含的可变语义;陈玉金等[5]构建基于证据理论的确定和可变三支决策模型;岳文琦等[6]在混合决策信息系统中,提出一种模糊效用三支决策模型;张春英等[7]在深入研究PS-粗糙集模型特点的基础上,提出一种基于PS-粗糙集的动态三支决策算法。此外,三支决策模型在水资源承载力、垃圾邮件过滤、图像分割等领域[8-11]得到广泛的应用。
“可拓集”从变换的角度研究对象具有某种性质的程度及其变化,并用关联函数进行定量化描述[12]。随着可拓学研究的深入,关联函数成为重点。文献[13]对可拓集无量纲一维关联函数进行研究,为进一步研究多维关联函数奠定基础。杨春燕等[14]介绍可拓集中初等关联函数构造的进展并进一步深入研究。在单评价特征基元可拓集基础上,杨春燕[15]研究了多评价特征基元可拓集的构造方法及其关联函数的建立方法,为解决不相容问题提供了理论依据。胡宝清等[16]从实际出发,研究区间论域上的可拓集及其关联函数。还有学者利用可拓集进行可拓评价,解决实际问题。安永林等[17]为综合评价服役隧道结构健康状况,利用可拓法进行评估并有针对地给出不同的策略。李倩倩等[18]以山东半岛蓝色经济区为研究对象,基于熵权可拓模型对城镇化发展水平进行评价。郭嘉伟等[19]基于熵权可拓物元模型对会宁县水资源承载力进行评价。文献[20-21]将可拓集方法应用于水资源承载力的评价。
三支决策模型大多以条件概率作为评价函数进行决策,而可拓集中关联函数表示事物具有或不具有某种性质的程度,可对同一域中的元素进行优劣排序,因此将可拓集应用于三支决策,不仅可以实现域的划分,同时能够挖掘决策优化方向,进而制定系统状态提升策略。基于此,本文利用可拓关联函数的方法,定义关联度比,构建一种基于关联度比的三支决策模型,并对哈尔滨市水资源承载力系统给出优化方向与建议。
1 预备知识
1.1 三支决策
三支决策的提出为决策粗糙集的正域、负域、边界域赋予合理的语义解释,分别对应接受、拒绝和延迟决策,符合人类的决策思想。
贝叶斯理论是风险型决策方法之一,其思想是以期望损失最小为决策依据,选择合适的决策方案[22]。三支决策是基于贝叶斯理论进行的决策,规则如下。
设状态空间Θ={Di,Di},表示对象x是否属于集合Di,行动集A={aP,aB,aN}表示对一个对象x进行分类决策时采取的行动。aP、aB、aN分别表示对象确定属于、不一定属于和一定不属于集合的行动,不同状态下对应不同行动的代价函数如表1所示。

表1 损失代价函数
λPP、λBP、λNP分别表示x本属于Di而采取行动aP、aB、aN时的损失;λPN、λBN、λNN分别表示x本不属于Di而采取行动aP、aB、aN时的损失。P(Di|[x])是条件概率,对于特定x,采取一个决策行动时的期望代价为
P)如果T(aP|[x])≤T(aB|[x])且T(aP|[x])≤T(aN|[x])成立,则x∈POS(X),
B)如果T(aB|[x])≤T(aP|[x])且T(aB|[x])≤T(aN|[x])成立,则x∈BND(X),
N)如果T(aN|[x])≤T(aP|[x])且T(aN|[x])≤T(aB|[x])成立,则x∈NEG(X)。
由于P(Di|[x])+P(Di|[x])=1,且λPP≤λBP≤λNP,λNN≤λBN≤λPN,则决策规则可简化为
P)如果P(Di|[x])≥α成立,则x∈POS(X),
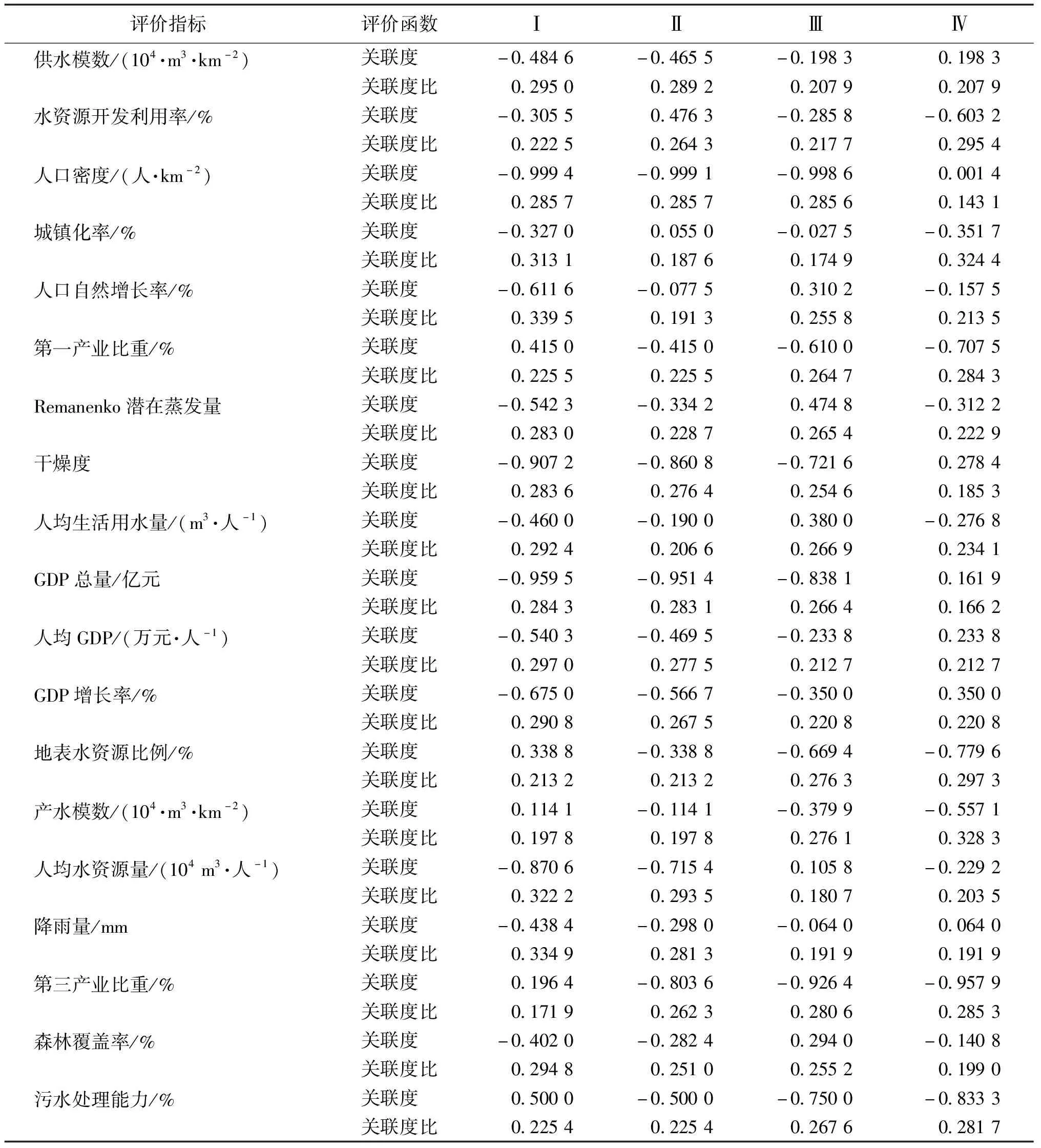
B)如果β N)如果P(Di|[x])≤β成立,则x∈NEG(X), 若x∈POS(X),则表示接受x;若x∈BND(X),则表示对x延迟决策;若x∈NEG(X),则表示拒绝x。 定义1[23](可拓集合) 设U为论域,u为U中任一元素,k是U在实数R的一个映射,T(TU,Tk,Tu)是给定的变换,称 (1) 定义2[13](正域为有限区间的关联函数) 若正域X0=[a,b]为有限区间,节域X(X≠R)为实数域上任何区间且X0⊂X,非端点x0∈X0,记X0和X的公共端点为xv(若无公共端点,则为空),则对任意实数x≠xv,则x关于X0和X且在X0的非中点x0取得最大值的一般关联函数为 (2) 其中:D(x,X0,X)为x关于X0和X的一般位置值。 定义3[13](正域为无限区间的关联函数) 设无限区间X0为正域,节域X(X≠R)为实数域上任何区间且X0⊂X,非端点x0∈X0,则对实数域上的任意点x关于无限区间套X0和X且在点x0取最大值的关联函数为 (3) 其中:D(x,X0,X)为x关于区间套X0和R的一般位置值。 三支决策是在概率粗糙集的基础上提出的,为粗糙集的三个域提供合理语义解释,三支决策中评价函数的选取直接影响决策结果,因此评价函数的选取至关重要。可拓关联度是可拓评价与决策的主要工具,其大小关系着决策的结果。因此,关联函数是一种重要而有效的评价函数。由于关联度值大部分为负,而且取绝对值后大于1,评价函数会影响决策,因此结合模糊集中隶属函数的思想,定义可拓关联度比如下。 定义4设Kj(Vi)为评价指标j关于等级i的关联度,则评价指标j关于等级i的关联度比为 (4) 由于关联度比的取值范围为(0,2),所以需要对关联度比进行归一化处理。由关联度比的定义可知,指标关于等级的关联度比和非关联度比的和为1。故归一化的关联度比适合作为三支决策的评价函数来进行决策。 将表1的代价函数作为损失,将关联度比作为评价函数构建三支决策模型。 对于特定对象j,采取一个决策行动时的期望代价为 (5) (6) 从式(6)可知,代价目标函数T(aP|j)、T(aB|j)、T(aN|j)的几何意义是以Pi(Kj)为变量,相关代价函数组合为斜率和截距的线性函数,因此三支分类的阈值α、β可以看作是上述三个代价目标线性函数之间交集的横坐标Pi(Kj)的取值。显然α、β可以看作是T(aP|j)与T(aB|j)、T(aB|j)与T(aN|j)交点的Pi(Kj)处取值,T(aP|j)与T(aN|j)的交点记为γ,如图1所示,图中的TP、TB、TN分别代表式(6)中的T(aP|j)、T(aB|j)、T(aN|j),T*表示TP、TB、TN中的任意量。 图1 TP、TB、TN之间的关系示意图 根据贝叶斯风险决策过程,最小代价决策规则如下。 P)如果T(aP|j)≤T(aB|j)且T(aP|j)≤T(aN|j)成立,则j∈POS(X); B)如果T(aB|j)≤T(aP|j)且T(aB|j)≤T(aN|j)成立,则j∈BND(X); N)如果T(aN|j)≤T(aP|j)且T(aN|j)≤T(aB|j)成立,则j∈NEG(X)。 由于0≤β<γ<α≤1,则决策规则可简化为 P)如果Pi(Kj)≥α成立,则j∈POS(X); B)如果β 步骤1确定待评物元、经典域和节域。将给定数据集的指标根据以往研究进行分级,并确定每个等级具体取值范围。经典域是每个等级中每个指标具体取值范围,节域表示所有等级中每个指标的取值范围,待评物元表示需要评价的物元,根据分级确定经典域和节域。 式中:Cj表示c1,c2,…,cn这n个指标的集合;Voj表示(aoj,boj),j=1,2,…,n的集合;而(aoj,boj)为等级t中样本关于第j个指标的取值范围。 式中:Cj表示c1,c2,…,cn这n个指标的集合;Vpj表示(apj,bpj),j=1,2,…,n的集合,而(apj,bpj)为所有等级中样本关于第j个指标的取值范围。 建立客史档案,把握顾客需求。市场营销理论告诉我们,只有真正把握顾客的需求,才能提供令宾客满意的服务,才能提高酒店的竞争力。因此,酒店必须要建立起独一无二的客史档案。那么酒店该从哪些方面建立客史档案呢?首先,酒店要从收集顾客资料着手,全程跟踪,完整准确的建立常客档案;其次,要应用计算机进行数据技术开发,建立详尽而细微的顾客需求档案,最终建立顾客信息库。 式中:Cj表示c1,c2,…,cn这n个指标的集合;Vi表示x*(i,j),j=1,2,…,n的集合;x*(i,j)为待评样本i关于第j个指标的取值。 步骤2根据关联度公式计算各指标的关联度。 (7) 式中:Kj(xi)表示第i个样本、第j个指标的关联度,各个指标值到各评价等级范围值的距离为 步骤3由可拓关联度比公式(4)计算每个指标关于每个等级的关联度比,并做归一化处理。 步骤4由熵权可拓评价法计算城市所属等级。 1)由于各指标的计量单位并不统一,而且正向指标和负向指标表示的含义不同,正向指标数值越高越好,负向指标数值越低越好,因此,对于正向、负向指标采用不同的运算进行数据标准化处理。同时为使后面计算的指标熵值有意义,即标准化后的指标值不为0,故标准化时后面要加1,取值范围为[1,2]。 式中:x*(i,j)表示第i个样本第j个评价指标值;xmax(i,j)=max{x(1,j),x(2,j),…,x(n,j)},即所有样本中第j个评价指标的最大值;xmin(i,j)=min{x(1,j),x(2,j),…,x(n,j)},即所有样本中第j个评价指标的最小值。 3)确定所属等级。城市关于众指标的综合关联度用公式(8)计算 (8) 若 (9) 则待评样本的等级为io。式中:Kio(d0)表示待评样本的关联度;maxKt(xi)表示待评样本关于所有等级关联度的最大值。 步骤5结合数据集特点,经过多次实验,并根据不同阈值划分后每个域中元素个数情况,可得选取阈值α=0.28、β=0.22比较合适,因此选取α=0.28、β=0.22作为阈值。由基于关联度比的三支决策的决策规则,对每个等级的指标进行域的划分,得到基于每个等级的三个域划分。 步骤6分析域的划分结果,对城市水资源承载力系统给出优化方向与建议。 步骤1中确定待评物元时,用到两层for循环,一层步长为指标数n,一层步长为样本数m,最终得到每一待评样本关于所有指标的取值,其时间复杂度为O(mn);步骤2、3中计算各指标的关联度与关联度比时,也用到步长分别为m和n的两层for循环,其时间复杂度也均为O(mn);步骤4中仍通过步长为m和n的两层for循环计算出正、负项指标及属性权重,其时间复杂度也为O(mn);因此最终得到的时间复杂度为O(mn)。 选取黑龙江省13市水资源承载力数据,包括水土资源和承载力两个指标体系,共19个指标,利用本文模型对哈尔滨市水资源承载力进行评价,并给出优化建议。 步骤1根据黑龙江省13市的水资源承载力数据,结合以往研究和专家经验,将指标承载力等级设定为4级,即Ⅰ(强)、Ⅱ(一般)、Ⅲ(弱)、Ⅳ(很弱)。各等级的经典域和节域为 其中:Dt矩阵表示经典域矩阵;Dp矩阵表示节域矩阵。 步骤2由关联度公式(7)及关联度比公式(4)计算哈尔滨市各指标关于每个等级的关联度及关联度比,见表2。 表2 哈尔滨市各指标关于每个等级的关联度及关联度比 步骤3由公式(8)~(9)计算可得,目前哈尔滨市水资源承载力处于Ⅱ级。 步骤4由决策规则得每个等级指标三个域的划分为 步骤5给出指标优化方向与建议。由熵权可拓评价法可知哈尔滨市目前水资源承载力处于Ⅱ级水平,根据每个等级指标三个域的划分以及水资源承载力现状可知,哈尔滨市需要优化指标有城镇化率、人口自然增长率、Remanenko潜在蒸发量、干燥度、人均生活用水量、GDP总量、人均GDP、GDP增长率、森林覆盖率。而在这些指标中,城镇化率、人口自然增长率的关联度比的值较大,在Ⅰ级正域中所处层次较高,所以应先优化这些指标,这为政府决策和管理提供依据。 本文将可拓集与三支决策结合建立基于关联度比的三支决策模型并应用于决策哈尔滨市水资源承载力。第一,基于关联度比构建三支决策模型,为三个域的构造提供合理的解释,丰富三支决策和可拓评价理论;第二,模型可以在每一级上划分三个域,定量给出评级改变时各指标的变化,并根据关联度比的值,可以量化同一域中属性的重要程度,使属性分出层次,既实现动态决策,又细化决策;第三,将模型应用于哈尔滨市水资源承载力评价中可知,若希望承载力由原来的Ⅱ级提升为Ⅰ级,则应优化城镇化率、人口自然增长率等指标,这为决策与管理提供理论依据。在阈值变化时,关于每个等级三个域如何变化,以及建立自适应的阈值计算方法将成为今后研究的重点。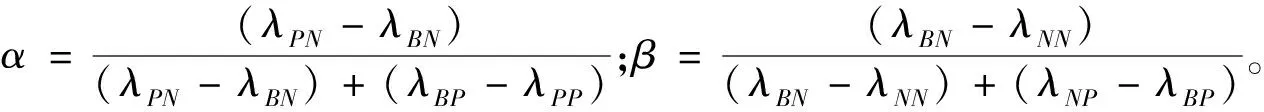
1.2 可拓集与可拓关联函数
2 基于可拓关联度比的三支决策模型的构建
2.1 评价函数的构造
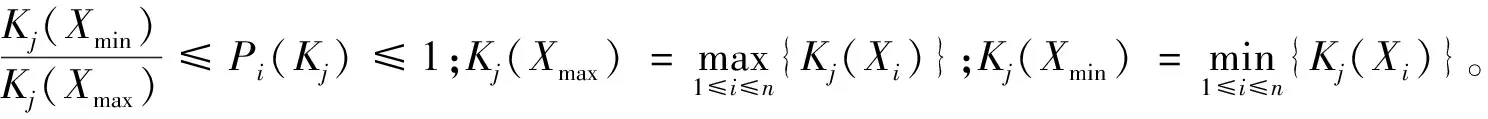
2.2 决策规则



2.3 模型步骤



2.4 算法分析
3 案例分析


4 结论
