基于演化博弈的建筑业安全监管机制研究
2021-05-24李文峰张文光钟国兴邱志全
李文峰 张文光 钟国兴 邱志全
(中建海峡建设发展有限公司 福建福州 350015)
0 引言
建筑业在大规模飞速发展的同时,也面临安全事故频发的风险,安全监管的要求也随之不断提高[1]。如何以改革创新为动力,通过科学、有效的方法分析建筑业安全监管过程中各方利益关系,探讨各情形下,提高安全生产监管水平的有效途径,最终实现夯实安全生产基础,保证施工生产的高效、稳定极为重要。
1 模型假设与模型构建
通过分析建筑业安全生产监管中的利益相关者后,使用演化博弈的方法对施工总承包方和劳务作业分包单位之间的行为进行动态分析[2],作出主要假设如下:
(1)建筑业安全监管的博弈主体为施工总承包方与劳务作业分包单位,博弈双方是有限理性的。施工总承包方的策略空间是严格监管-不严格监管,劳务作业分包单位的策略空间是合规作业-不合规作业。
(2)劳务作业分包单位如果选择合规作业,通过履行劳务合同可以获得净收益为S1,如果劳务作业分包单位选择不合规作业,则在获取正常的净收益S1之外,则会通过不合规的工序优化、劣质材料代换等手段获得超额利润△S。若劳务作业分包单位的不合规作业,被施工总承包方发现,则会获得惩罚成本P,其处罚措施包括罚款、班组开除、限制投标资格、追究刑事责任等。劳务作业分包单位的不合规作业,在监理与第三方监管过程中,同样会对施工总承包方的声誉及利润收益产生影响,造成其损失成本记为L1。
(3)施工总承包方选择严格监管策略,确保在施工过程中,加强对项目质量、安全等方面的管控,则可以获得包括社会影响力的提升,上级单位、政府主管部门的嘉奖,将该类额外收益列为S2。但在加强安全管控过程中,难免会产生因人力、资源投入增加产生超额成本C1。若施工总承包方选择不严格监管策略,仍可以获得一定额外收益S3。但在加强管控过程中,在该情况下,将其投入成本列为C2,S2、S3仅为社会影响力提升,上级单位、政府主管部门的嘉奖收益,额外利润收益假设为△S。同时,S2>S3,C1>C2。
(4)在项目施工过程中,不合规的生产经营模式往往会遭遇社会舆论压力,因此在本模型中通过设置第三方参数,即社会舆论监督力量作为安全监管的重要手段,对模型进行分析。将社会舆论发生的概率记为β∈[0,1]。若劳务作业分包单位的不合规作业,与施工总承包方的不严格监管同时出现并产生负面社会舆论影响,劳务作业分包单位则会遭到βP的处罚,施工总承包可能来自监理与第三方的监管过程中产生的惩罚损失L2。
(5)假设劳务作业分包单位采取合规作业策略的概率为x∈[0,1],则选择不合规作业策略的概率则为1-x;施工总承包方选择严格监管策略的概率为y∈[0,1],则选择不严格监管策略的概率则为1-y。
基于以上假设,构建施工总承包方和劳务作业分包单位的博弈收益矩阵,如表1所示。

表1 施工总承包方和劳务作业分包单位的博弈收益矩阵
根据上述假设与博弈收益矩阵,则可进一步假设劳务作业分包单位选择合规作业Ex、不合规作业E1-x所获得的期望收益及平均收益EG分别为:
Ex=yS1+(1-y)S1=S1
E1-x=y(S1+ΔS-P)+(1-y)(S1+ΔS-βP)
EG=yEx+(1-y)E1-x
=y(S1+ΔS-P)+(1-y)(S1+ΔS+βP)
同理,假设施工总承包方选择严格监管Ey、不严格监管E1-y所获得的期望收益及平均收益EQ分别为:
Ey=x(S2-C1)+(1-x)(S2-C1-L1)
=L1x+S2-C1-L1
E1-y=(L1+βL2)x+S2-C2-L1-βL2
EQ=xE+(1-x)E
=S2-C2-L1-βL2-x[S2-C2-S2+C1+(1-β)L2]
因此,施工总承包方和劳务作业分包单位的博弈复制动态方程组为:
接着,令博弈复制动态方程组中G(x,y)与Q(x,y)取值为0时,可以得到演化博弈的均衡点O(0,0),A(0,1),B(1,0),C(1,1)。
接着在求得x,y的偏导数后,通过构建Jacobi矩阵J,
对角相乘、相减求得矩阵J的行列式及矩阵J的轨迹分别为:
detJ=(1-2x)(1-2y)[βP+(1-β)Py-ΔS][S2-C1-S3+C2+βL2(1-x)]
trJ=(1-2x)[βP+(1-β)Py-ΔS]+(1-2y)[S2-C1-S3-C2+βL2(1-x)]
如果满足行列式detJ>0,且trJ<0,则该均衡点是渐进稳定点,也是演化博弈的稳定均衡解。根据对均衡点的Jacobi矩阵行列式detJ与轨迹trJ的分析,劳务作业分包单位的策略受到选择不合规作业的超额收益△S、施工总承包方的处罚P以及负面社会舆论处罚βP的影响;施工总承包方的策略选择受到自身严格监管的净收益S2、不严格监管的净收益S3及负面社会舆论处罚βP的影响。针对Jacobi矩阵中的不同情形作出假设,对各情形下均衡点的局部稳定性进行讨论。
2 模型稳定性分析
使用MATLAB软件对博弈模型求解分析过程中,可能出现以下4种稳定情形,如表2所示。不同情形的博弈稳定分析如下:
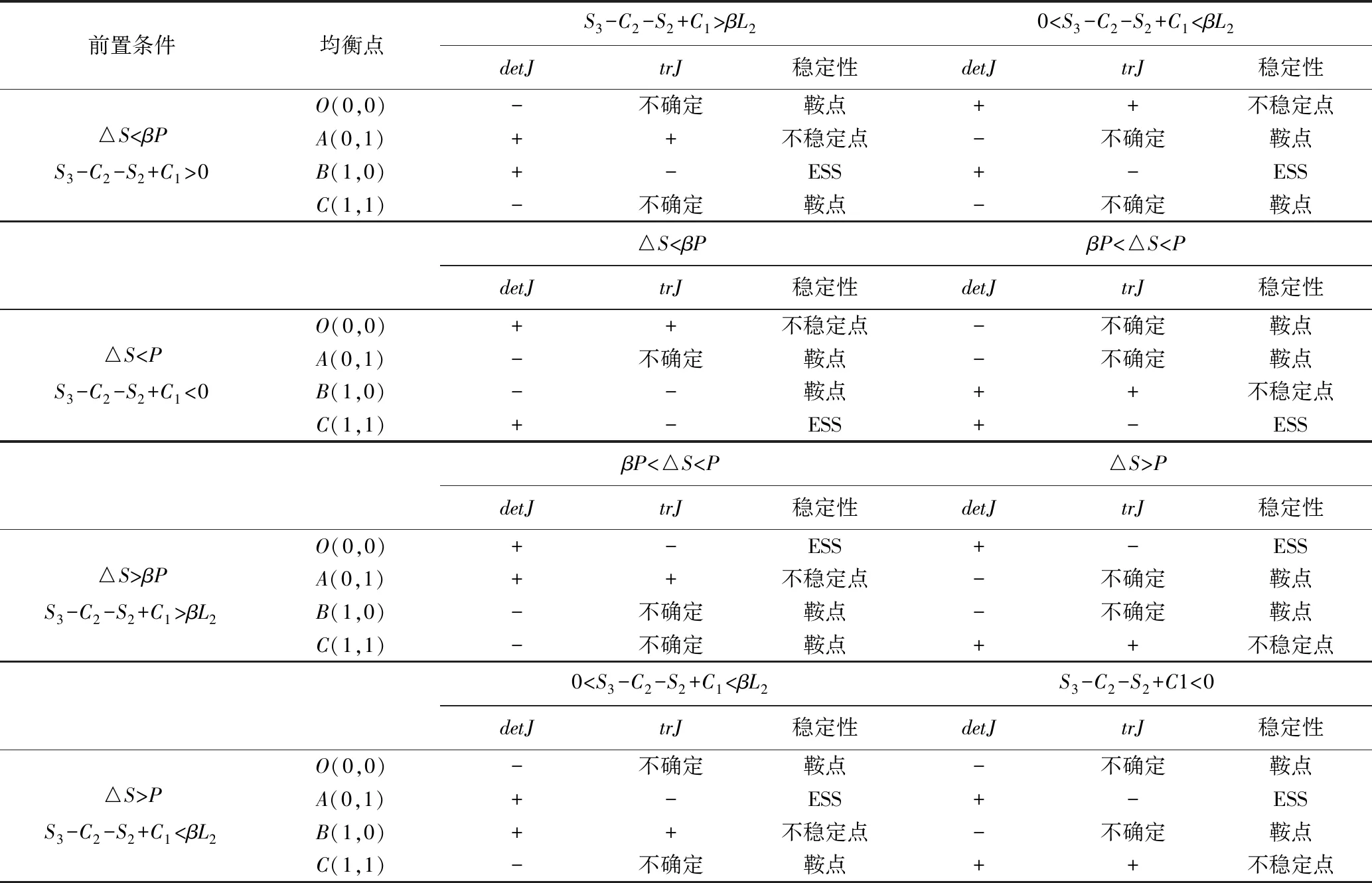
表2 均衡点局部稳定性情况分析
(1)若△S<βP且S3-C2-S2+C1>0
当劳务作业分包单位选择不合规作业所获得的超额收益△S小于受社会舆情导致处罚βP,则必然会实行合规作业。施工总承包方则可在一定程度上将该部分期望收益所得剥离,只要施工总承包方不严格监管所获得的净收益大于严格监管的净收益,出于成本投入和监管成本的考虑,就会选择不严格监管的策略。均衡点B(1,0)是演化博弈的稳定点,对应的演化博弈策略为合规作业-不严格监管。
(2)若△S 当施工总承包方选择不严格监管策略所得净收益S3-C2小于严格监管的净收益S2-C1,施工总承包方必然选择严格监管策略。在这种情况下,劳务作业分包单位只要不合规作业超额收益△S小于不严格作业被施工总承包方发现的惩罚P,就会自觉选择合规作业。也就是说劳务作业分包单位即使选择不合规作业,所获得的超额收益也无法超过施工总承包方的惩罚,作为理性的博弈参与者,最佳策略自然是选择合规作业,均衡点C(1,1)是演化博弈的稳定点,对应的演化博弈策略为合规作业-严格监管。 (3)若△S>βP且S3-C2-S2+C1>βL2 当施工总承包方选择不严格监管策略所得净收益S3-C2大于严格监管的净收益S2-C1,与受社会舆论曝光而导致上级部门问责所受损失之和时,施工总承包方会选择不严格监管策略。劳务作业分包单位只要选择不合规作业获得的超额收益△S大于社会舆论造成的期望惩罚βP,就会选择不合规作业。随着上级单位及政府主管部门问责机制不断完善,施工总承包方受上级部门及政府主管部门的惩罚L2通常会远远大于不严格监管获得的净收益S3-C2。因此均衡点O(0,0)对应的均衡策略不合规作业,不严格监管出现的可能性越来越小。 (4)若△S>P且S3-C2-S2+C1<βL2 当劳务分包作业单位选择不合规作业所得超额收益△S大于施工总承包方的惩罚力度Р时,劳务作业分包单位在遭遇施工总承包方惩罚之后,仍然有利润可图,劳务作业分包单位为了获得更多利益,必然选择不合规作业的策略。由于施工总承包监管机制不完善,对劳务作业分包单位违规作业处罚力度不足,造成不严格监管下的净收益小于严格监管下的净收益(S3-C2-S2+C1<0),或小于严格监管下的收益与社会舆论造成上级问责期望损失之和时,施工总承包方都会选择严格监管。为了避免这种情况出现,施工总承包方需要进一步了解劳务作业分包单位因不合规作业获取潜在利益的情况,进而提高惩罚力度Р。均衡点A(0,1)是演化博弈的稳定点,对应的演化博弈策略为不合规作业-严格监管。 在建筑业安全监管过程中,通过社会舆论监督对各参与方的行为选择造成一定制约,但制约强度大小需要在不断博弈波动中进行调整,强度不适合的社会舆论监督均会对博弈稳定性产生一定影响,会对建筑业安全监管与合规作业产生消极作用。 同时,在建筑业安全生产监管过程中,需要采取动态方法,对社会舆情的损失进行合理定量评估,对监管力度和处罚行为等监管手段与不合规作业存在潜在收益进行合理分析后,在二者的动态博弈关系中,及时获得最优监管指标,确保监管行为有效、可行。3 结语
