基于改进灰狼算法的成品油管道泄漏定位方法*

郭 颖，杨理践，张 贺

(1. 沈阳工业大学 信息科学与工程学院，沈阳 110870； 2. 辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001)

成品油管道是一种用来运输成品油的高效、安全、科学的渠道，是目前国内管网体系的重要组成之一.管道泄漏现象普遍存在于油品的运输过程中，而现有的泄漏检测与定位方法一般都是针对某一特定管道进行的，而在实际的成品油输送管道中，当局部管段压力过高或受腐蚀、磨损、震动等影响，管道测量的信号具有非线性特征，这种情况下通常使用负压波检测法来检测泄漏，但是效果不理想[1-3].随着我国石油化工行业的高速发展，将有越来越多的长距离输送成品油的管道逐渐投入使用，研究成品油管道泄漏点的检测与定位方法对于油气管道的完整性管理具有重要的理论意义和工程价值[4-5].

实现成品油输送管道泄漏点的检测与准确定位的必要条件是对泄漏信号的有效提取和判别.成品油输送管道采集的压力信号、次声波信号及超声波信号等是用于管道泄漏检测的主要信号.成品油输送系统是非线性系统，信号的泄漏特征容易被淹没在噪声里，噪声的存在会对后期的管道泄漏识别以及定位产生干扰[6-7].成品油输送管道压力信号中存在小振幅的噪声，泄漏特征信息被噪声影响不易识别出来.刘金海等[8]提出采用低通滤波、陷波滤波和小波滤波对管道首末两端压力信息进行高精度实时滤波，保证泄漏特征信息不被过滤掉.由于采用小波变换进行去噪时，需要根据经验来选取合适的小波基函数，而经验模态分解(empirical mode decomposition，EMD)是一种自适应的信号分析方法，它不再需要选择基函数.郭晨城等[9]提出采用EMD提取管道泄漏信号的奇异点信息，减少噪声对泄漏特征信号的影响.由于EMD方法受分解尺度选择和重构分量选择的影响，林伟国等[10]提出一种基于时域积分的泄漏声波信号增强方法，通过不断提高泄漏信号的信噪比，有效减少了泄漏检测的误报率和漏报率.由于天然气具有可压缩性，当天然气输送管道发生泄漏时，通过压力变送器检测到的管道首末端压力变化并不明显，因此，应用于输油管道泄漏检测的负压波方法难以应用于输气管道的泄漏检测与定位.由于局域均值分解(local mean decomposition，LMD)的信号分解条件较EMD更为宽松，在降低端点效应对信号分解过程影响的同时也避免了过包络现象等[11].孙洁娣等[12]采用改进LMD对天然气管道首末端进行声发射信号分解，去除了与泄漏无关或噪声干扰的乘积函数分量，获取了含有主要泄漏信息的瞬时频率(product function，PF)分量，实现了对泄漏点的精准定位.

由于成品油管道外部的噪声组成比较复杂，目前已有泄漏去噪的研究成果，主要是针对特定液体或天然气管道的泄漏进行的，如何有效地进行成品油管道泄漏监测，保证生产的安全进行，是当下成品油输送管道管理急于解决的问题.

由于泄漏点的位置具有随机性，它距离上、下游监控站的距离各不相同，使得成品油会对负压波产生反射、散射、吸收等不同程度的影响.因此，通过对超声波波速信号进行消噪并进行信号拐点时间提取，利用管道首末站信号拐点的时间差值建立目标函数，通过改进灰狼算法优化求解获得泄漏点位置，通过环道实验室实验及现场数据验证了该方法的可行性.

1 定位方法

1.1 管道沿程环境对压力波波速的影响

流体的弹性模量、密度和管道材质影响负压波传播的速度.由于体积弹性系数和密度等是随距离变化的函数[13-14]，所以负压波波速表达式为

(1)

式中：K为介质体积弹性系数；ρ为介质的密度；E为管道材质的弹性模量；d为管道直径；Q为与该约束条件相关的修正系数；e为管壁厚度.

1.2 压力和超声波波速之间关系

成品油管道发生泄漏时，一般会根据泄漏所产生的负压波到达管道首末站的时间差进行泄漏点定位.由于管道完整性管理的要求，不允许在原有管道上打孔安装压力测量传感器进行泄漏检测与定位，因此，利用夹持式超声波传感器的波速来间接测量管道内部压力变化.该方法可以在不损坏管道内部流体流场，无压力损失的情况下对管道内部压力进行无损检测.

由于管道泄漏导致管道首末站两端压力发生变化，压力的变化则会引起超声波波速发生变化，超声波的波速与压力之间的数学关系式[15]为

US=GP

(2)

式中：US为超声波波速值；G为比例系数；P为管道内部压力值.通过式(2)可以看出，压力与超声波波速之间存在线性关系，因此，可由超声波波速的变化反应管道内部压力的变化情况.

1.3 超声波波速信号拐点时刻的获取

1.3.1 LMD算法

LMD算法的本质是将信号分解为无数个有物理意义的PF乘积，由此可反映出信号在空间各个尺度上分布规律，从而更能细致地对采集信号特征进行分析[16].

信号x(t)被分解为M个PF分量和一个残余分量rk(t)，其表达式为

(3)

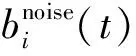
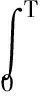
(4)

(5)

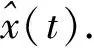
1.3.2 超声波波速拐点提取

通过对管道首末站的超声波波速信号进行预处理，进行LMD分解，通过互相关分析选取主要PF分量，重构信号，然后再利用小波变换提取信号拐点.

(6)

式中：φ(t)为基本小波函数；a为尺度因子.超声波波速拐点提取的原理框图如图1所示.

图1 超声波波速信号拐点提取原理框图Fig.1 Schematic principle of turning point extraction for ultrasonic velocity signal

1.4 改进灰狼优化算法

灰狼优化(grey wolf optimizer，GWO)算法[18]是一种新型群体智能优化算法，它通过模拟自然界灰狼群体捕食猎物的行为实现优化搜索的目的.GWO和粒子群算法(particle swarm optimization，PSO)及其改进算法(improved particle swarm optimization，IPSO)[19]相比，具有易于实现、程序调整参数少等优点[20].纵然GWO算法在许多领域中取得较好的应用效果，但是依然存在易陷入局部最优、收敛速度慢、求解精度不高等缺点.

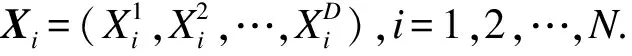
(7)

A=2ψr1-ψ

(8)

C=2r2

(9)

其中，r1和r2为[0，1]之间的随机数；ψ为距离控制参数，随着迭代次数的不断增加从2线性减少到0，即

(10)

其中，θmax为最大迭代次数.

狼群中其他灰狼个体Xi根据α、β、γ的位置Xa、Xβ、Xγ来更新各自的位置，即

(11)

(12)

根据式(11)～(12)可以得出，对个体位置迭代过程中采用GWO算法时，只考虑了个体当前位置和群体以往遍历的最优位置信息，而最优位置的更新是起决定作用的.所以GWO算法在求取最优解问题时容易陷入局部最优的缺陷.

新提出的灰狼优化算法(improved grey wolf optimizer，IGWO)是通过将粒子群优化算法中的对粒子运动最优解进行记忆保存的思想加入到GWO中，进而增强了GWO算法的收敛速度和求解精度.该方程表达式为

(13)

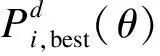
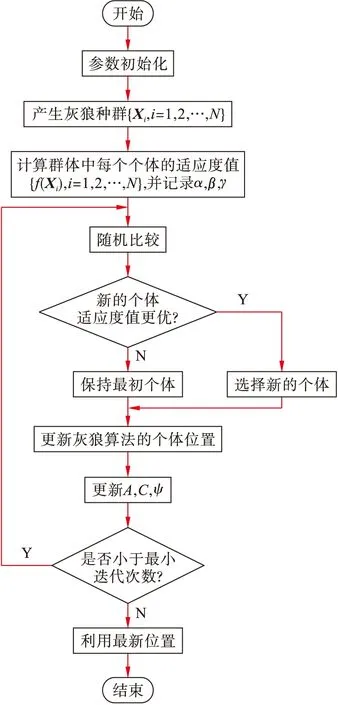
图2 改进灰狼算法应用流程图Fig.2 Application flow chart of IGWO

1.5 成品油管道泄漏点定位计算

成品油输送管道泄漏点定位计算原理如图3所示.由泄漏点处所产生的负压波传播到管道首末站的时间分别为t1、t2，此时间即为管道首末站检测到超声波波速发生变化所需时间，其表达式分别为

(14)

(15)

泄漏点定位公式为

(16)

图3 泄漏点定位原理图Fig.3 Schematic principle of localization of leakage points

每次将X=n(其中，n为已知值)代入式(17)，计算Δt，并计算yn值，即

yn=|Δtn-Δt|

(17)

通过改变n的值，依次计算yn，其中，yn中最小值对应的n即为泄漏点位置.算法步骤如下：1)管道首末站超声波波速拐点确认；2)确定发生泄漏的位置是距离管道首站近还是管道末站近；3)如果是距离管道首站的超声波波速先变化，泄漏定位搜索位置为原管道长度的1/2；4)采用改进灰狼优化算法求解式(17)，进行泄漏点位置的估计计算.

2 仿真实验

2.1 环道实验

搭建2 800 m实验环形管道，管径为DN50.环形管道上共设有14个模拟泄漏点.首站流量为120 L/min，管道运行压力为1.2 MPa.环形管道利用美国国家仪器公司DAQ-9184对管道首末站的超声波波速信号进行采集，利用DAQ-9028对管道的首末站流量进行采集.实验装置如图4所示.

图4 实验装置Fig.4 Experiment apparatus

实验中，介质为水，超声波波速为1 520 m/s，负压波波速为1 200 m/s，管道首站温度为30 ℃，末站温度为20 ℃.当距离管道首端1 400 m处的泄漏阀打开时，管道泄漏时刻采集的流量信号如图5所示.

图5 管道首末站流量变化曲线Fig.5 Flow change curves at first and last stations of pipeline

从图5中可以看出，当管道发生泄漏时，首末端流量会发生明显变化，首端的流量增加，末端的流量减少.首末端采集到的超声波波速信号经过LMD信号消噪处理后，首末端的信号如图6、7所示.

图6 管道首站超声波波速信号与消噪后信号对比曲线Fig.6 Comparison of ultrasonic velocity signals before and after de-noising at first station of pipeline

图7 管道末站超声波波速信号与消噪后信号对比曲线Fig.7 Comparison of ultrasonic velocity signals before and after de-noising at last station of pipeline

从图6、7中可以看出，经LMD信号消噪后，首末端超声波波速信号有一个非常明显的拐点.超声波波速信号经LMD消噪后，再次通过小波分析进行拐点提取，管道首末站的信号拐点位置如图8、9所示.

由图8、9可知，通过LMD信号消噪和小波变换处理之后的信号拐点更清晰，所提出的方法不仅能直接去除信号中的噪声，而且能清晰地给出拐点，实现管道首末站超声波波速信号拐点时刻准确获取，从而进行管道泄漏点定位.

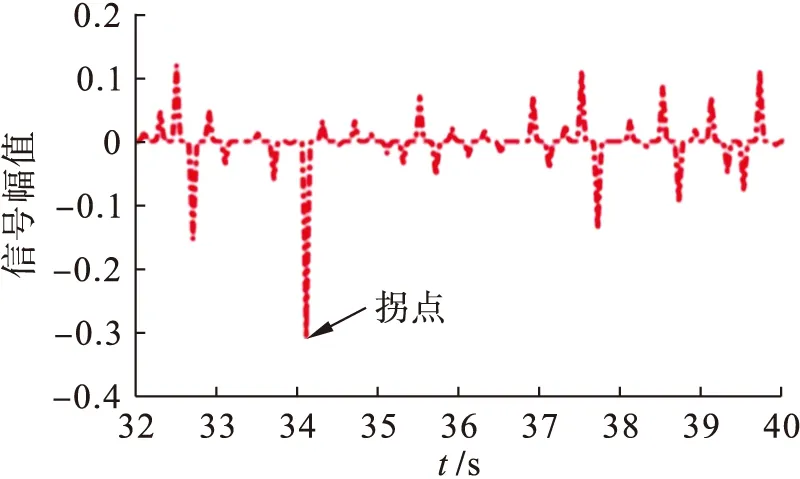
图8 首站超声波波速信号经小波变换之后的拐点Fig.8 Turning point of ultrasonic velocity signal after wavelet transform at first station

图9 末站超声波波速信号经小波变换之后的拐点Fig.9 Turning point of ultrasonic velocity signal after wavelet transform at last station

GWO算法的参数选取种群数量N=30，维数D=500；IGWO算法参数设置和GWO算法一样；PSO算法参数选取学习因子c1=c2=2，惯性权重初始设置为ω0=1，最小惯性权重ωmin=0.3，惯性权重线性下降.IPSO算法参数设置和PSO一样.

图10给出了IGWO、GWO、IPSO和PSO在不同迭代次数下对函数目标值的寻优收敛曲线.在对函数目标值的求解过程中，IGWO算法具有更快的收敛速度和更高的收敛精度.表1给出了环形管道四种算法30次实验的泄漏点位置估计计算平均结果比较.

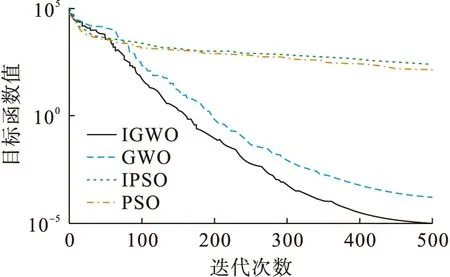
图10 IGWO、GWO、IPSO和PSO对目标函数收敛曲线Fig.10 Convergence curves of target function by IGWO，GWO，IPSO and PSO

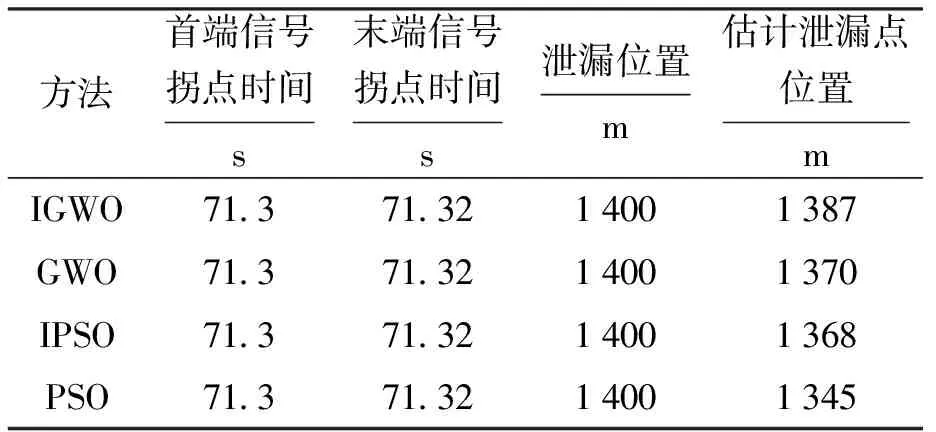
表1 环形管道泄漏点位置估计结果Tab.1 Estimation results of leakage point locations in annular pipeline

从表1可以看出，与GWO、IPSO及PSO算法相比，IGWO在管道泄漏位置估计上获得了较准确的泄漏位置估计.

2.2 现场测试数据实验

在某成品油管线上某段进行泄漏测试，测试段的管道里程为148 km，输量约为1 223 m3/h，管道首站输油温度为13 ℃，管道末站输油温度为9 ℃.在管道测试段采用打开泄放阀门进行泄漏模拟测试，该管段的上游出站压力为12 MPa，下游进站压力为8 MPa，泄漏测试点距管上游里程为45.5 km.

根据管道参数按照式(1)计算负压波的波速.定位公式采用式(17)进行计算.表2给出了四种算法2次实验的泄漏点位置估计平均结果比较.

表2 泄漏点位置估计结果Tab.2 Estimation results of leakage point locations

从表2可以看出，与GWO、IPSO及PSO算法相比，IGWO估计的泄漏点位置与实际管线泄漏模拟位置相接近.根据现场实际条件，泄漏量大于正常输量的2%，定位误差可控制在120 m左右.

3 结 论

本文通过分析得出以下结论：

1) 分析了超声波波速与管道内部压力之间的关系，提出了采用超声波波速来检测管道泄漏的方法.

2) 对灰狼优化算法进行了改进，提高了算法对泄漏点的定位速度以及估计精度.

3) 为了更加准确地提取出超声波波速信号拐点，采用LMD与小波包分析算法相结合，用来确定泄漏时产生的负压波传播到管道首末站的时间差，从而提高了泄漏点的定位精度.