基于激光雷达点法向量的车辆实时位姿估计＊

张瑞宾 郭应时 陈元华 刘晓刚 周扬

（1.长安大学，西安 710064；2.桂林航天工业学院，桂林 541004）

主题词：激光雷达 运动车辆 点法向量 位姿估计

1 前言

智能车辆通过激光雷达等环境感知系统对运动车辆位姿（Moving Vehicle Pose，MVP）进行准确估计，可有效提高危险交通场景下的安全性。国内外学者针对运动物体的位姿展开了相关研究。王岩等人[1]提出了一种基于迭代最近点（Iterative Closest Point，ICP）的井下无人机实时位姿估计方法，将煤矿井下四旋翼无人机位姿估计问题转换为机载激光点云数据的扫描匹配问题。宋亮等人[2]提出了基于扩展卡尔曼滤波（Extended Kalman Filter，EKF）的相对位姿估计算法，对相对位置和姿态进行估计的同时，可辨识出目标的未知参数。郝刚涛等人[3]提出一种基于单目相机与无扫描三维激光雷达融合的非合作目标相对位姿估计方法，可实现尺度模糊下相对位姿的快速鲁棒估计。畅春华等人[4]提出一种基于二维激光雷达的移动机器人实时位姿估计算法，通过优化位置序列间的方向角实现机器人的位姿估计。S.Akshay 等人[5]提出了一种基于无人机周围点云特征的激光雷达定位误差协方差矩阵自适应估计方法，该方法比基于距离的协方差矩阵模型更精确。Opromolla等人[6]提出了基于在轨服务的激光雷达三维点云姿态估计算法，通过姿态跟踪算法对姿态进行校正，通过将模型点云和目标点云进行ICP 匹配实现姿态跟踪。Y.Fang等人[7]提出了全等四面体对齐（Congruent Tetrahedron Align，CTA）算法，通过激光雷达扫描点云和模型点云中的全等四面体确定相对位姿，采用ICP算法进行CTA后的姿态跟踪。N.Philip等人[8]提出了基于相平面控制技术的相对位置控制和基于相对四元数反馈的相对姿态控制方法，证明了固定增益观测器对位置和姿态的估计是有效的。

以上位姿估计方法在点云几何信息较完整、分布特征显著时是可行的。但由于激光雷达扫描视场有限，每帧仅能获取单一视角下的场景，导致点云数据存在遮挡残缺等现象，获取目标表面采样点数量取决于激光雷达与目标间的相对位置，从而影响位姿估计准确率。因此，本文提出一种基于点法向量特征的方法，以解决动态刚性目标点云残缺导致位姿信息难以提取的问题。

2 基于点法向量的目标姿态估计算法

2.1 算法的提出

在传统位姿估计算法中，要求模型库具有较大样本数量，且待测目标三维点云数据具有较高完整性，为了减少算法对以上条件的限制，基于目标车辆表面所具有的刚性特点，结合车载激光雷达采集运动目标车辆点云数量随距离变化的特性，本文提出基于点法向量的动态车辆实时位姿估计方法，流程如图1所示。

图1 算法流程

2.2 点云数据的获取

车载激光雷达安装位置如图2所示，在车辆纵向中心平面上，A点位于车辆背门最高处，B点位于发动机罩最前端，C点和D点分别为A柱在纵向中心平面投影处的最高点和最低点，F点为车载激光雷达的几何中心。取A点在地平面的投影点O作为坐标系原点，以O为起点，在纵向中心平面内沿地平面指向车头为X轴正方向，过点O垂直纵向中心平面指向驾驶员侧为Y轴正方向，过点O垂直地平面指向车身为Z轴正方向。A′与A′′、B′与B′′、C′与C′′分别关于A、B、C点对称。激光雷达中心坐标为(x0,y0,z0)，其轮廓底部投影对应直线llow，安装激光雷达时，为了保证点云采集的对称性，应将雷达置于车顶中心处，且确保其工作时不会扫描到车身（即关键点A、B、C、D），即满足：

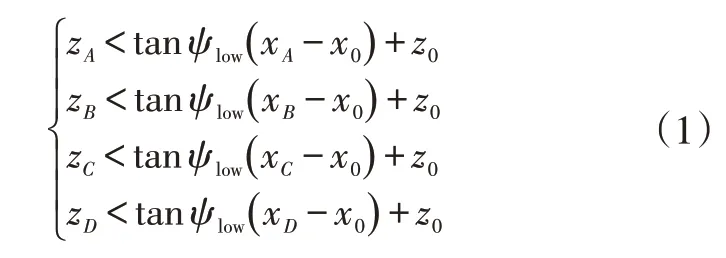
式中，ψlow为垂直视场角；zA、zB、zC、zD、z0分别为A、B、C、D、O点的z坐标；xA、xB、xC、xD、x0分别为A、B、C、D、O点的x坐标。

选用速腾聚创公司RS-LiDAR-32 型激光雷达，该激光雷达可实现垂直视场角-25°～15°、水平视角360°扫描周围环境，测距最大范围200 m，每秒输出64×104个点，设置扫描频率为20 Hz。

图2 车载激光雷达安装示意

2.3 平面点的判定及点法向量估计

本文通过刚性目标表面局部拟合平面上的点法向量进行姿态估计，以弯曲度特征滤除非平面上的点法向量。表面点云任意点P的弯曲度CP满足：

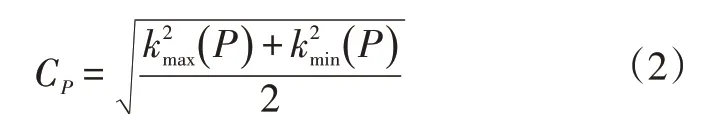
由式（2）可知：当CP近似为0或小于一定的阈值时，可判定P点为平面点；当CP大于一定的阈值时，可判定P点为非平面点。该阈值可依据实际点云中的噪声及其他误差影响确定。

2.4 自适应聚簇中心的点法向量分类方法

利用最小二乘法拟合求得目标车辆三维点云各点的法向量后，由于车辆属于刚性物体，表面由不同角度的近似平面组成，各表面估计的点法向量的方向不同，因此需要对全部点法向量进行聚类分析。传统的Kmeans 算法的聚簇数量k是根据经验事先人为设定的，由随机方式确定初始聚类中心，车载激光雷达采集周围运动车辆点云数据的角度实时发生变化，复杂场景下目标物间存在遮挡问题，导致获取目标点云平面的数量存在差异，聚簇数量应与获取的平面数量相关联，应采用自适应聚簇中心的聚类算法流程确定聚簇数量，算法自适应性主要体现在根据目标点云质心向量与点法向量之间的夹角分布来自适应求取k和各聚簇中心值c(k)。算法具体步骤为：

a.求取车辆目标点云坐标原点指向质心的向量C；

b.求取每个点法向量与C之间的夹角θi；

c.求取θi分布直方图，如图3 所示，筛选出频数f大于阈值λ的点法向量分布区间种类数量即为聚簇数量k；

d.求取所筛选出的各类分布区间内的点法向量数量；

e.求取每类点法向量均值，得到c(k)；

f.求取标准测度函数，评价其收敛性，得到最大迭代次数后停止，否则，循环a～e。最终得到点法向量聚类结果如图4所示。

图3 θi分布直方图

2.5 坐标轴的确定

由于复杂场景下聚类获得的点云数据受到噪声和遮挡因素的影响，点云并不集中在某一平面内，导致待拟合平面的点法向量分布不均匀，因此应选取抗噪性能较好的随机采样一致性（Random Sample Consensus，RSC）算法对聚类后的点进行二次处理。

图4 点法向量聚类结果

RSC算法先从样本集合中随机抽取一个样本子集，采用最小方差估计算法计算该子集模型参数，对比样本与模型间的偏差，利用预先设定的阈值与偏差比较，当偏差小于等于阈值时，该样本点被定义为内点（Inliers），否则为外点（Outliers）。RSC 可以剔除外点的影响，最终得到全局最优的参数估计值。RSC算法的关键在于确定阈值d、迭代次数K[9]：

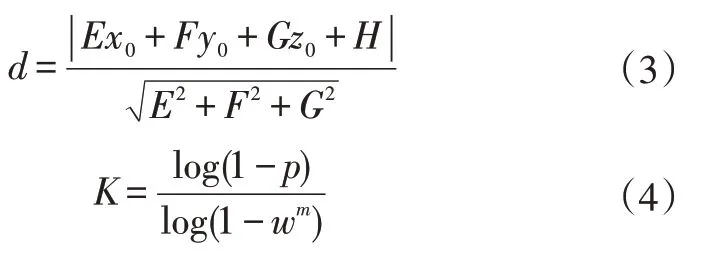
式中，E、F、G、H为常量；p为置信度；w为内点在数据集内的占比；m为计算模型最小样本数量。

算法具体步骤为：

a.从待拟合的点云集合中随机选取3 个点，计算其构成的拟合平面方程z=ax+by+c；

b.计算点云中各点至该平面的距离di=|axi+byi+zi|；

c.利用式（3）计算出阈值d，当di≤d，判定该点为内点，并统计内点数量；

d.利用式（4）计算迭代次数K，通过迭代运算统计出最多数量的内点集合，并对该情况下获取的内点进行平面拟合。

图5 所示为采用目标车辆表面点云拟合的平面点法向量，由图5 可知，三维点云场景下的待测目标坐标系中X轴和Z轴即为刚性物体所占比重最大的2类点云垂直拟合平面的代表点法向量n和o，Y轴可通过n和o叉积的形式获得，目标车辆表面拟合平面点法向量与OXYZ坐标系的关系如图6所示。

2.6 目标姿态的求取

确定出拟合平面代表法向量n(nx,ny,nz)、o(ox,oy,oz)、a(ax,ay,az)后，通过欧拉角旋转矩阵对运动目标的横滚角ϕ、俯仰角θ和航偏角ψ进行解算：

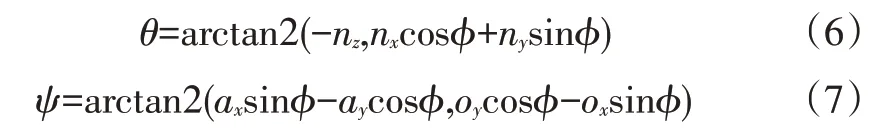
由式（5）～式（7）解算出的(ϕ,θ,ψ)即为目标物三维姿态角。

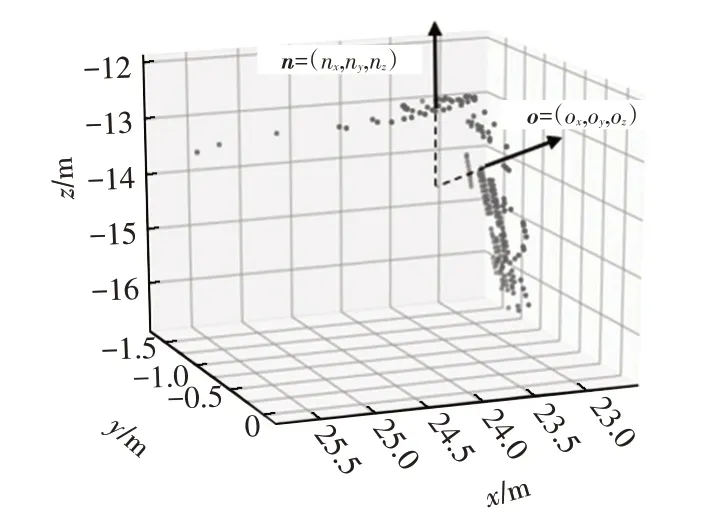
图5 目标车辆表面点云拟合的平面点法向量

图6 拟合平面点法向量与OXYZ坐标系的关系

3 姿态估计算法试验

为了定量地分析所提出的动态车辆实时姿态估计算法的效果，利用试验车采集某城市复杂交叉口点云数据，结果如图7 所示，该车顶部装配有三维激光雷达。激光雷达以10 帧/s 的扫描帧率，获得目标车辆运动时车辆运动点云图，如图8所示。采用基于点法向量的动态车辆实时位姿估计方法，得到如图9所示的连续位姿估计结果，通过计算车辆质心点处点法向量位置变化，实时估计车辆位姿。

图7 试验车采集的某城市复杂交叉口点云数据

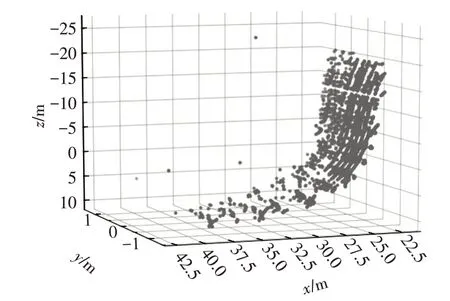
图8 激光雷达连续帧扫描目标车辆点云

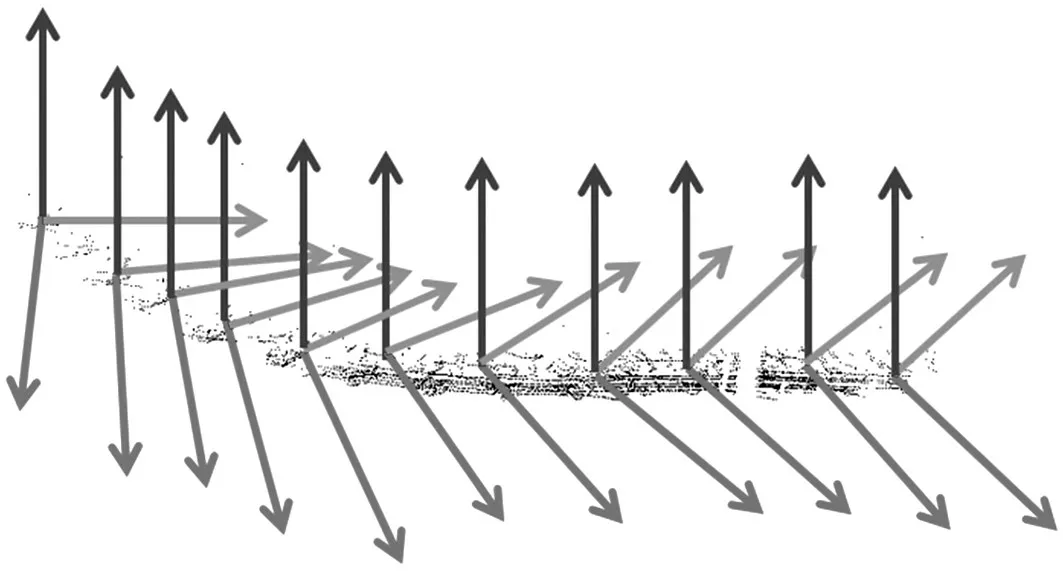
图9 连续位姿估计结果

为了验证算法的有效性，采用均方根误差（Root Mean Square Error，RMSE）R衡量观测值与真值之间的偏差。R越小，代表位姿估计的测量精度值越高：

式中，Xobs,i、Xreal,i分别为目标车辆第i帧时点云对应的位姿估计值和真实值。

图10、图11所示分别为目标车辆经过交叉口时，直线运动和曲线运动状态下的实际运动轨迹与试验车实时获取的目标车辆质心坐标点间的偏差关系，图中所示车辆质心点位置与实际运动轨迹具有一定的拟合度，因此可以通过计算质心点处点法向量实时估计车辆位姿。

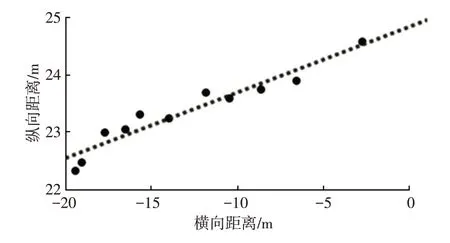
图10 直线运动轨迹与质心点位姿坐标偏差关系

由图7 可知，当目标车辆通过某城市交叉口时，运动轨迹主要由直线轨迹和曲线轨迹组成，表1所示为目标车辆实时位姿估计RMSE分析结果。

由表1 可知：目标车辆直线运动时，基于点云法向量的方法计算得到的运动目标车辆横滚角ϕ、俯仰角θ和航偏角ψ的均方根误差较低，且均小于传统迭代最近点方法；曲线运动时，由于目标车辆方向角变化较大，造成点云数据遮挡残缺现象较为严重，基于点云法向量的方法计算得到的ϕ、θ和ψ的均方根误差值均高于直线运动的均方根误差值，但仍小于传统迭代最近点方法。因此，当目标车辆通过某城市交叉口时，在直线和曲线2种轨迹运动情况下，基于点云法向量算法对目标车辆的位姿估计效果均优于迭代最近点算法，且受点云数据遮挡残缺现象的影响程度均低于传统迭代最近点算法。

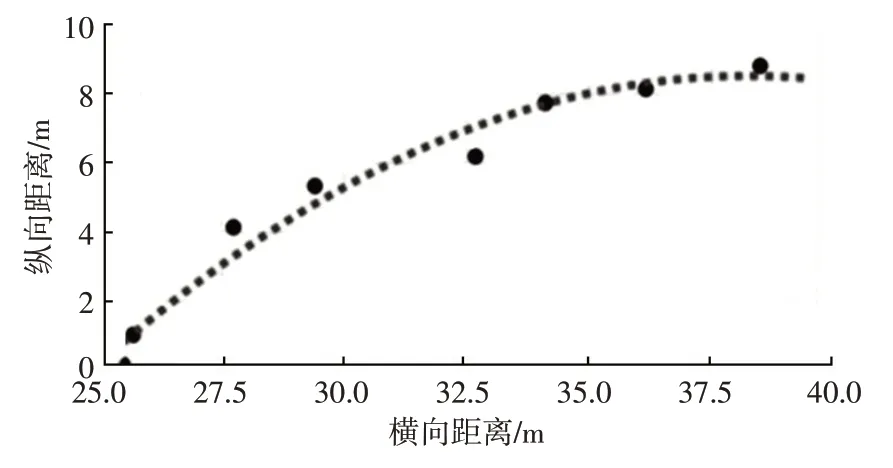
图11 曲线运动轨迹与质心点位姿坐标偏差关系

表1 目标车辆运动实时位姿估计RMSE分析结果 (°)

三维姿态估计的参数中，横滚角ϕ、俯仰角θ的均方根误差较小，航偏角ψ的均方根误差较大。目标车辆在水平路面行驶，因此引起的横滚角ϕ、俯仰角θ的变化量较小，导致均方根误差较小；目标车辆在交叉口转向，因此引起的航偏角ψ的变化量大，由式（7）可知，航偏角受多个因素影响，由于目标车辆车体表面并非完全垂直，使得每个因素估计时都存在一定误差，导致均方根误差较大。

4 结束语

本文针对复杂城市交叉口场景下激光雷达获取运动车辆点云残缺而导致位姿信息难以提取的问题，提出一种基于点法向量特征的动态刚性目标实时位姿估计方法，采用自适应聚类算法求解点法向量聚簇中心的数量，通过随机采样一致性算法对属于同一聚类的点进行平面拟合，通过运动学方程完成目标的三维姿态角求解，采用均方根误差来衡量不同方法获得车辆位姿估计值与真值之间的误差关系，结果表明，运动车辆进行直线与曲线运动时采用点法向量位姿估计效果均优于传统基于迭代最近点的方法，具有较高的准确性，能克服点云残缺性。由于本方法仅对动态刚性目标进行实时位姿估计，并未考虑运动状态变化过程，后续应对动态目标状态估计及预测方法展开深入研究。