双绕组无轴承磁通切换电机转子径向悬浮滑模控制研究
2021-05-23周扬忠黄政凯
张 竞,周扬忠,黄政凯
(福州大学 福建省新能源发电与电能变换重点实验室,福州350108)
0 引 言
无轴承电机是依据磁轴承和传统交流电机结构的相似性,将无轴承技术和电机相结合的一种新型电机,因其具有无机械接触、易实现更高的转速与更大的功率密度等特点,在航空航天、仪器仪表、生物医药、化学化工等行业有广阔的发展前景[1⁃2]。
双绕组无轴承磁通切换电机(以下简称BF⁃SPMM)是无轴承电机的一种,其既具有无轴承电机无机械接触、无磨损、无需润滑的特点,又具有磁通切换电机转子无永磁体、空载反电动势正弦度高、转矩密度高等特点[3]。
目前,关于BFSPMM的研究绝大多数集中在电机本体上,而对BFSPMM驱动控制策略研究较少,尤其是转子径向悬浮控制策略。文献[4]提出了一种两段隔离转子的新型无轴承电机,转子所受悬浮力的大小和方向分别通过悬浮电流的幅值和相位来控制,并进行了实验验证。文献[5]通过对电机磁路模型的简化,推导了悬浮力的数学模型,并将转子位置划分为6个区间,分别制定不同的控制策略,实现电机悬浮控制。
在已有文献中,转子悬浮控制系统通常利用径向位移闭环控制中的PI控制器来产生径向悬浮力给定。虽然PI控制器结构简单、工作可靠,但其受电机参数影响大、抗干扰能力差,且这种控制方法建立在转子无偏心情况下,实际运行中转子会发生偏心,且电机存在模型不精确的情况。针对这些问题,本文基于滑模变结构控制思想[6⁃7],提出构建径向悬浮滑模控制器来代替现有径向位移闭环控制中的PI控制器的控制方法,实现转子径向悬浮快速稳定控制。
1 双绕组BFSPMM结构及悬浮原理
1.1 双绕组BFSPMM结构
双绕组BFSPMM横截面及绕组连接示意图如图1所示。其转子为凸极铁心结构,共有10个齿,转子上无永磁体和绕组。定子由12个“U”形铁心构成,定子上还有mA,mB,mC三相功率绕组和sa,sb,sc三相悬浮绕组,每相功率绕组和每相悬浮绕组均由4个线圈按照图1中的连接方式串联构成;imA,imB,imC为三相功率绕组电流,功率绕组中通入电流产生切向电磁转矩;isa,isb,isc为三相悬浮绕组电流,悬浮绕组中通入电流后产生的磁场会打破原有磁场的对称性,从而产生径向悬浮力。

图1 双绕组BFSPMM横截面及绕组连接示意图
1.2 悬浮原理
如图1所示,定义与功率绕组线圈A1、A3同轴线的水平轴为x轴,超前x轴90°的竖直轴为y轴,图1中所标电流方向为正方向,气隙①、②处所标箭头为空载情况下永磁磁通φPM方向。根据文献[8]研究结果表明,在悬浮绕组中通入合适的电流即可产生转子径向悬浮所需要的悬浮力,实现转子径向悬浮。三相悬浮绕组通入电流产生的悬浮力可用矢量图表示,如图2所示。

图2 悬浮绕组电流与悬浮力关系
1.3 数学模型
1.3.1 坐标系定义
BFSPMM的坐标系定义如图3所示。
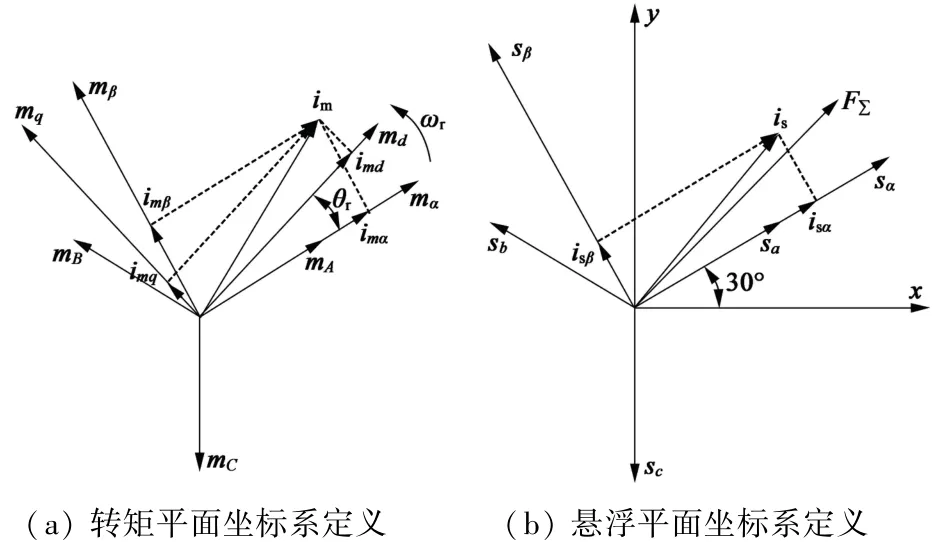
图3 坐标系定义
图3(a)为转矩平面坐标系定义。mα,mβ为两相静止坐标系,mα与mA的轴线重合;md,mq为同步旋转坐标系;mA,mB,mC为三相功率绕组轴线,imA,imB,imC为三相功率绕组电流,通过对三相功率绕组电流进行矢量合成得到功率绕组的电流矢量im;im在mα,m坐标β轴上的投影分别为imα,imβ,im在md,mq坐标轴的投影分别为imd,imq。md与mα夹角为θr,ωr为转子旋转电角速度。
图3(b)为悬浮平面坐标系定义。x,y为水平-垂直直角坐标系,其中x,y轴的方向已在图1中给出。sa,sb,sc为三相悬浮绕组轴线,isa,isb,isc为三相悬浮绕组电流,悬浮绕组的电流矢量is由isa,isb,isc矢量合成得到;sα,sβ为两相静止坐标系,sα与sa的轴线重合;x,y坐标系滞后sα,sβ坐标系30°;is在sα,sβ轴上投影分别为isα,isβ;悬浮绕组电流矢量is产生的悬浮力为F∑。
1.3.2 悬浮力数学模型
实际运行过程中,BFSPMM转子会发生动态偏心,造成气隙磁路不对称,从而引起绕组电感、绕组耦合的永磁磁链发生改变。本文通过有限元方法,对偏心情况下的绕组电感、绕组耦合的永磁磁链进行分析。图4为转子偏心示意图,以水平向右的方向为直角坐标系x轴的正方向,以垂直向上的方向为直角坐标系y轴的正方向建立平面直角坐标系。转子的圆心由原来的O点偏移至点O′,点O′坐标为(x,y),总的偏移量e可表示:e=(x2+y2)1/2;偏心角度φ=tan-1(y/x)。

图4 转子偏心示意图
通过有限元分析,转子偏心情况下仅功率绕组与悬浮绕组间的互电感Mms以及永磁体匝链到悬浮绕组中的磁链ψfm与转子偏心位移有关,则有:

式中:Mmm为功率绕组电感;Mss为悬浮绕组电感;ψfm为功率绕组耦合的永磁体磁链。
根据虚位移原理,转子所受的径向悬浮力等于磁共能Wm对径向位移的偏导数,即径向悬浮力Fx,Fy可表示:
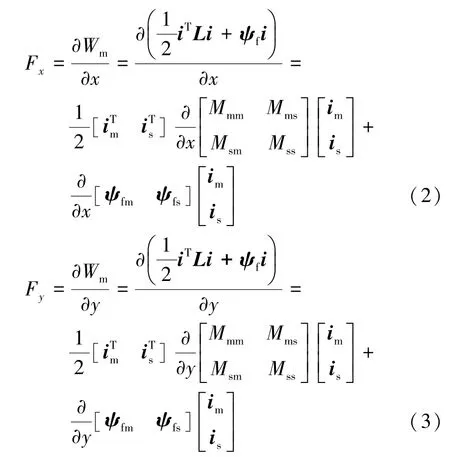
利用有限元分析结果以及对绕组电流进行坐标变换,对式(2)、式(3)进一步推导得到悬浮力表达式:


电磁转矩Te的表达式[8]:

式中:pr为电机极对数。
2 BFSPMM悬浮运行控制策略
2.1 BFSPMM的转子动力学模型
本文所用BFSPMM为两自由度结构(2⁃DOF),转轴一端固定而一端实现自由悬浮。但是,在实际电机工作中,特别在转子高速旋转下,在转子上施加径向力时需要考虑到径向两个轴之间由于陀螺效应引起的耦合,及实际电机由于偏心旋转带来的离心力。
图5为实际工作过程中的转子状态,定义静止坐标系x,y,z及转子同步旋转坐标系i,j,k,其中k轴与转子旋转轴重合,转子底部由调心轴承固定。定义转子绕i,j,k三个轴旋转的转动惯量Ii,Ij,Ik。由于转子结构对称,故Ii=Ij。
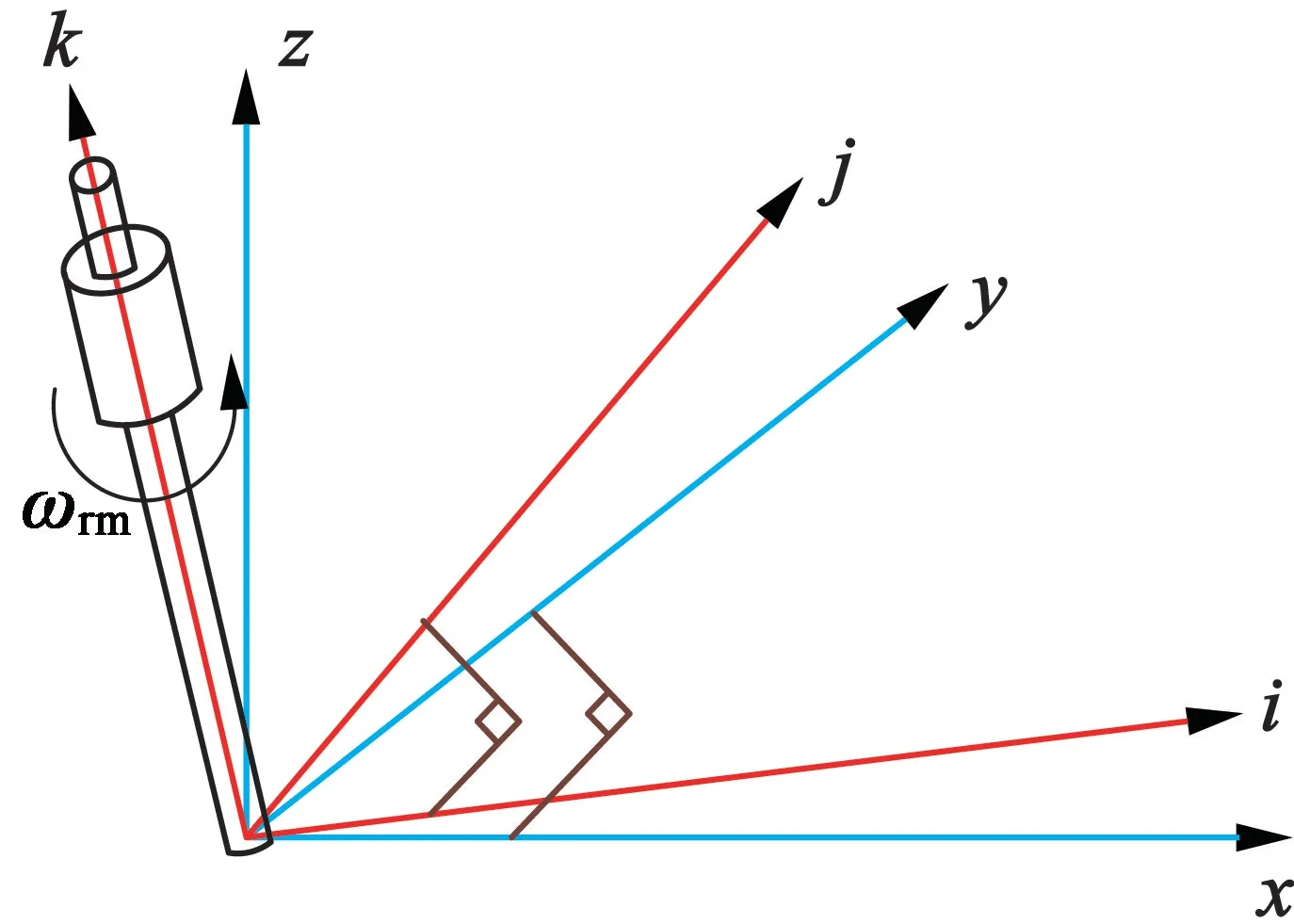
图5 实际工作过程中转子状态
参考文献[9⁃10]中提出的磁轴承转子动力学方程,推出BFPSMM的转子动力学方程:

式中:Tx及Ty为转子受到的力矩;θx,θy为转轴与x,y轴的夹角;ωrm为转子转速。在BFSPMM中,转子受到的力矩主要由三部分组成,分别为偏心下由重力产生的力矩(垂直放置)、偏心时转子受到的单边磁拉力矩以及由悬浮电流产生的悬浮力力矩。
1)偏心转子受到的重力矩:

式中:h为转轴质心的高度;lrt为转轴的长度;x和y为转子径向偏移量。
2)单边磁拉力力矩:

式中:kx(θr)和ky(θr)是x,y方向上的单边磁拉力系数。在BFSPMM中,转子在偏心时的单边磁拉力不相等,且与转子位置角θr相关。
3)悬浮力力矩:

式中:Fx和Fy分别为转子上在x,y方向上产生的悬浮力。
结合式(7)~式(10)可得本文的双绕组BF⁃SPMM在竖置状态下的转子动力学模型:

2.2 滑模变结构控制策略
BFSPMM是一个多变量、强耦合的非线性系统,其控制方法的有效性直接关系到电机的工作性能。为了提高径向悬浮控制的稳定性、抗干扰能力,本文根据转子动力学模型及悬浮系统状态变量,得到径向悬浮系统状态方程,在径向悬浮系统状态方程的基础上,基于滑模变结构控制思想,设计径向悬浮滑模控制器,控制器的输入为实际测得位移信号x,y与给定的位移信号x∗=0,y∗=0的偏差ex,ey,输出为径向悬浮力给定
径向悬浮系统的状态变量定义如下:

式中:ex,ey为转子径向位移误差。
结合转子动力学模型式(11)以及悬浮系统状态变量,得到径向悬浮系统状态方程:

根据滑模控制器的输入,选取滑模切换面函数:

式中:c1,c2,c3,c4为常数,且都大于0。
结合式(13),对选取的切换面函数求导,得:
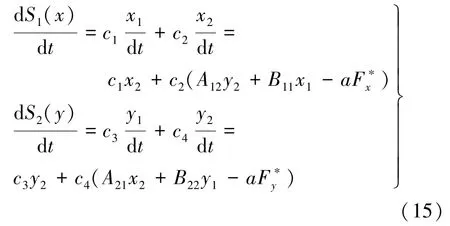
为了保证系统良好的动态性能和减小抖振,在设计控制器的过程中还需要采用趋近律[11],趋近律表达式如下:

通过调节趋近律的参数ε和k,既可以保证滑动模态到达过程的动态性能,又可以减小系统的抖振。
再结合式(15)与式(16),得到x轴、y轴悬浮力给定
由式(19)可知,若取ε1>0,k1>0,ε2>0,k2>0,则:

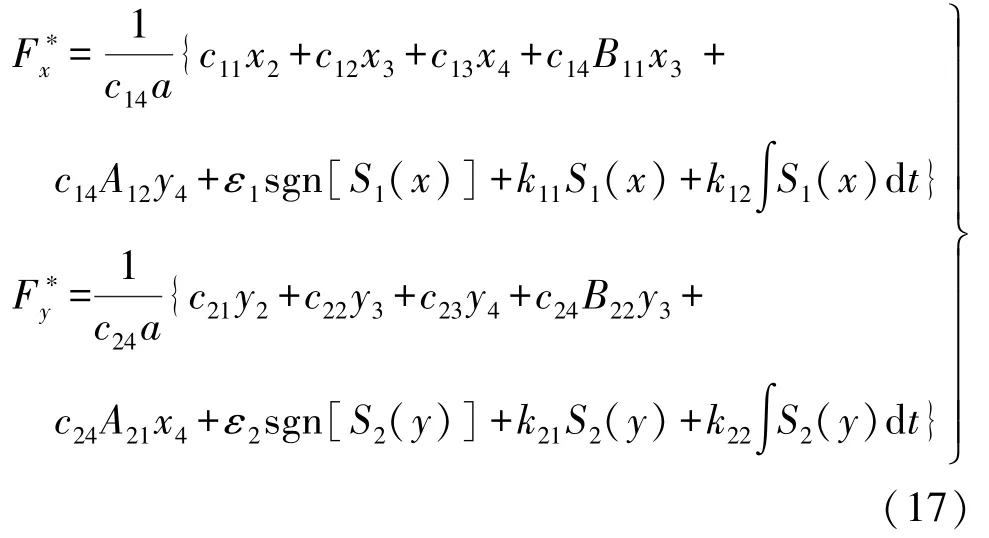
下面运用Lyapunov稳定性定理证明径向悬浮滑模控制器的稳定性。
选取Lyapunov函数:

所以,设计的滑模控制器在Lyapunov函数下是渐近稳定的。
2.3 BFSPMM系统控制框图
基于上述理论分析,构建整个双绕组BFSPMM系统控制框图如图6所示。通过转子径向位移传感器检测转子径向位移实际值x,y,将转子径向位移给定值x∗,y∗与转子径向位移实际值x,y进行误差计算,得到转子径向位移误差ex,ey;将转子径向位移误差ex,ey送入径向悬浮滑模控制器,得到径向悬浮力给定值再根据悬浮平面坐标系的定

对其求导可得:义,利用sα,sβ坐标系超前xy坐标系30°,将进行坐标变换得到利用2/3变换,将进行坐标变换得到三相悬浮绕组电流给定再将和isa,isb,isc送给电流滞环比较环节,输出控制三相逆变桥臂控制信号,实现转子径向悬浮。功率绕组采用矢量控制策略,实现转子切向旋转控制。
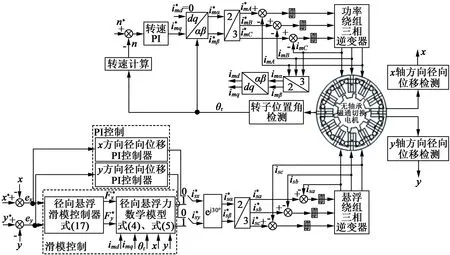
图6 双绕组BFSPMM系统控制框图
3 仿真研究
根据图6在MATLAB/Simulink中搭建双绕组BFSPMM控制系统的仿真模型,电机参数如表1所示。
为了验证本文控制策略的有效性,对采用滑模变结构控制策略和采用传统PI控制策略的径向悬浮系统进行仿真对照。电机给定转速为1 500 r/min,切向负载5 N·m,x方向带100 N径向负载,0.5 s时x方向带载由100 N突卸至0。仿真结果如图7、图8所示。

表1 电机参数

图7 采用滑模控制策略的仿真结果波形

图8 采用PI控制策略的仿真结果波形
图7为采用滑模控制策略的仿真结果波形,图8为采用PI控制策略的仿真结果波形。从图7与图8的控制对比仿真结果可见:
(1)在起动过程中,滑模控制系统x,y方向径向位移脉动很快控制为0,但PI控制系统x,y方向径向位移脉动需要长达0.2 s才收敛到0附近,表明滑模控制系统切向旋转与径向悬浮之间解耦性能更好;
(2)0.5 s时突卸径向负载,滑模控制系统x方向径向位移超调基本为0,而PI控制系统x方向径向位移超调了0.006 mm,表明滑模控制系统径向位移控制特性更硬;
(3)径向负载越大,PI控制系统径向位移脉动明显大于滑模控制系统,表明滑模控制系统具有更优良的稳定性能。
4 结 语
本文针对双绕组BFSPMM驱动系统,基于滑模变结构控制思想,提出了一种转子径向悬浮控制方法,理论分析与仿真结果表明:与传统PI控制方法相比,采用滑模控制方法,有效地降低了转子径向偏移量、径向偏移脉动,提高了系统响应速度以及抗干扰能力,整体控制效果更好。
