基于混合指数模型的风险曲线构建

姚正锟 南开大学金融学院

一、引言

财产保险的一个特点是，损失的大小取决于事故或损失的严重程度。投保的保额只有在非常严重或完全损失的情况下才支付。在大多数情况下，损失是以低于最大保额的方式结算的。由于这种“部分损失”的特点，任何一种风险的保险金额增加或减少都不需要按比例改变保险费。这种非比例或非线性关系会导致定价的复杂化，特别是当它与承保范围的限制相结合时。对保险金额的限制可以采取多种形式。免赔额、特许权、超额保险、保留金、共同保险和最高限额都是限制保险范围的方式。为了正确评估有限保险保障的成本，有必要衡量已消除损失的比例或剩余损失的比例。而风险曲线就是为了解决这一问题而产生的。

风险曲线的概念最早由Ruth E.Salzmann（1963）提出，该研究以北美保险公司（INA）的索赔数据为基础，对1960 年至1961 年间发生的火灾损失进行了分析，得出按保险价值百分比计算的累积损失成本的经验数据分布，并表明对于同质风险组，这种分布是稳定的。随后S.Ludwig（1991）对Salzmann曲线进行进一步修正，并将此方法应用到更新的数据。而在行业中被广泛应用的Swiss Re curves（瑞士再保险曲线）和Lloyds curves（劳合社曲线）在S. Bernegger（1997）提出的MBBEFD 分布得到证明。MBBEFD（Maxwell-Boltzmann，Bose-Einstein，Fermi-Dirac distribution）是物理学中统计力学的分布，该分布被Bernegger发现非常适合[0,1]区间上的经验损失分布建模，其通过使用MBBEFD 分布成功拟合了Swiss Re curves 和Lloyds curves，此后MBBEFD 被作为欧洲主要的风险曲线的模型基础。而Clive L.Keatinge（1999）提出了一种通过混合指数模型进行保险数据损失分布拟合的新的方法，本文就是在其基础上运用EM算法对风险曲线进行构建。

二、风险曲线的定义

假设F(x)是区间在[0,1]上的损失分布函数，有限期望函数L(d)=E[min(d,x)]，X是实际损失，M是最大可能损失，并且X≤M，D是财产险的免赔额或险位超赔再保险的最大自留额。其中d=D/M，x=X/M分别代表了标准化后的免赔额和标准化后的损失。

根据定义可看出，M·L(d)是财产险免赔额以下或再保险分出公司自留部分的期望损失，M·(L(1)-L(d))是财产险免赔额以上或再保险分入公司的期望损失。因此，这部分纯风险保费比率就是风险曲线G(d)。

其中，G(0)=0，G(1)=1。

因为1-F(x)≥0，并且F'(x)=f(x)≥0，所以G(d)在区间[0,1]上是一个递增的凹函数。

风险曲线描述的是免赔额与损失扣减率（给定免赔额以下的赔付成本占总赔付成本的比率）的关系。风险曲线的横轴数值代表免赔额占总保险金额或者最大可能损失（MPL）的比例，它的纵轴对应的数值代表损失扣减率（LER）。在对含有免赔额的财产险保单和险位超赔再保险合同的定价过程中，定价人员经常借助风险曲线解决相关问题，风险曲线是基于历史索赔数据的传统建模方法的有力替代方法，尤其对于新兴的中小保险公司来说，在定价中具有很大的参考意义。

▶图1 风险曲线示例

以图1 为例，对于非比例的险位超赔再保险来说，假设每层保额为2000万元，占全部保额比例为10%，横轴10%对应的曲线纵坐标为55%，横轴20%对应的曲线纵坐标为70%，那么再保险承保在10%到20%部分的保费为（70%-55%）×原保费。

对于直保公司免赔额定价来说，从图1 可看出，其自变量为10%时所对应的因变量为55%，那么对于该类风险，当免赔额相当于保额的10%时，该免赔额可以去除55%的预期损失强度。换句话说，扣去免赔额后的预期损失强度仅相当于无免赔额时的45%。

三、混合指数模型与参数估计

（一）理论模型

根据损失数据的特性，我们使用的是混合指数分布的离散形式，其中x是损失数据，pi是与λi对应的混合权重。

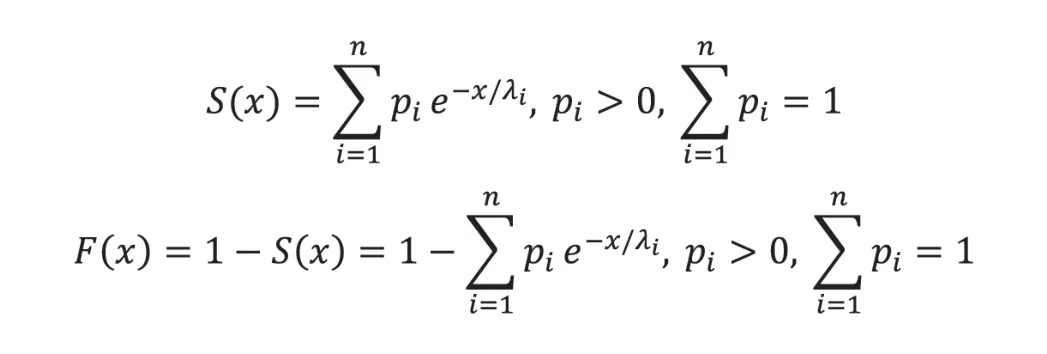
基于混合模型的特性，我们将使用EM 算法对模型进行参数估计。

（二）参数估计

1.参数估计方法

EM 算法又称期望最大化（Expectation Maximization）算法，是基于极大似然估计（Maximum Likelihood Estimation, MLE）理论的优化算法，十分适合解决具有缺失数据或者隐变量的模型的求参问题，而这种特性可以很好地应用在混合模型之中。给定相互独立的观测数据x=(x1,...,xn)，模型的参数为θ，概率密度函数为p(xi;θ)，根据MLE 理论，极大化的对数似然函数为：

假设观测数据中存在隐变量z=(z1,z2,…,zk)，隐变量可以表示缺失数据，或概率模型中任何无法直接观测的随机变量，在混合分布中，隐变量的意义是表示样本中的数据属于哪个分布，根据边缘概率的求解，再加入隐变量之后，概率密度函数p(xi;θ)可以表示为：

其中第一行是隐变量为连续变量的情况，第二行为隐变量为离散变量的情况。

在这里我们以离散变量为例进行相关的推导说明。此时极大化的对数似然函数为：

由于隐变量zj的存在，所以我们无法直接求出参数θ，这时我们引入与隐变量有关的概率分布Qj(zj)，由Jensen 不等式观测数据的对数似然有如下不等关系：

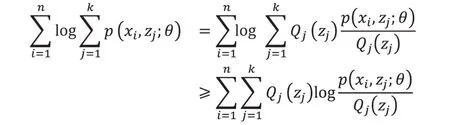
这个过程相当于确定了似然函数的下界，再假设θ固定的情况下，那么所求的似然函数的值是由Qj(zj)和p(xi;zj)决定的，我们需要不断调整这两个概率来逼近真实值，而当满足上式的等号时，所得结果大致满足真实值。

若要满足不等式的等号条件，需要满足p(xi;zj;θ)/(Qj(zj))=m，其中m为常数。

因为Qj(zj)是关于隐变量的概率分布，所以满足，因此

由上面两个式子，我们可以得到：

从中我们可以看到，在满足等号条件下，Qj(zj)应该是隐变量对观测数据的后验概率，所以在确定了Qj(zj)的情况下，我们让因此我们的求解目标为：

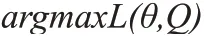
总的来说，EM 标准算法是一组迭代计算，迭代分为两部分，即E步和M 步，其中E 步“固定”前一次迭代的θ(t-1)，求解Q(t)，使L(θ,Q)取极大值；M步使用Q(t)，求解θ(t)，使L(θ,Q)取极大值。EM算法需要给定一个参数初值θ(0)后开始迭代，迭代中E 步和M 步交替进行，当∥θ(t)-θ(t-1)∥小于某个给定的阈值时停止迭代。

2.应用EM算法求混合指数模型的参数

朱利平、卢一强、茆诗松（2006）提到，以单参数混合指数分布为例，使用EM算法进行参数估计，密度函数为：

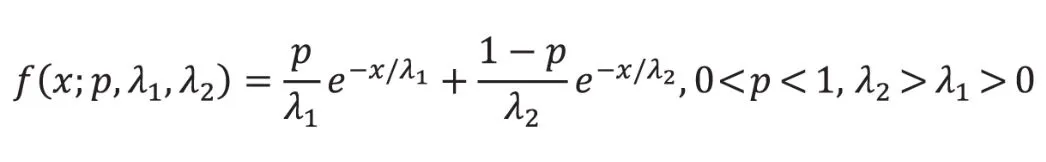
其中：

xi服从混合指数分布fi。如果Ii为示性变量，那么，Ii=1表示xi来自密度函数f1i的指数总体，Ii=0表示xi来自密度函数f2i的指数总体。可知，Ii服从二项分布，P(Ii=1)=p，P(Ii=0)=1-p。因为我们不知道xi来自f1i还是f2i的指数总体，因而，Ii是不能被观测到的随机变量。

xi和Ii的联合分布为g(xi,Ii,θ)=(pf1i)Ii [(1-p)f2i](1-Ii)，从而Ii在xi给定的条件分布为：

给定初值θ(0)，EM算法步骤为：

E步——求期望值。

其中，

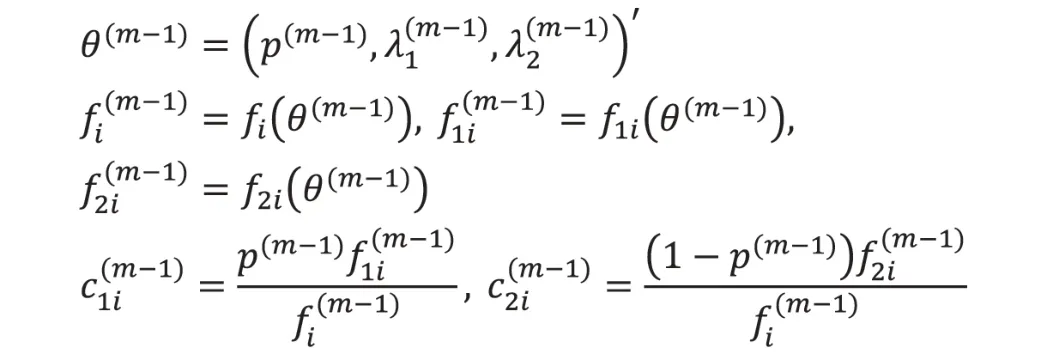
M步——极大化求θ(m)，使得Q(θm,θ(m-1))=maxQ(θ,θ(m-1))。

以θm作为θ(m-1的更新值，重复第1和第2步，当∥θ(m)-θ(m-1)∥小于某个给定的阈值时停止迭代。由于EM算法的收敛性是有理论保证的，因此上述迭代过程一定收敛。

四、模型检验与分析

本文采用同质性的一般责任险的336条损失数据，并使用Python进行风险曲线的构建，数据来源于Klugman、Panjer、Willmot（1998）。首先我们使用EM算法对经验数据进行混合指数的参数估计，结果如表1所示。

▶表1 EM算法对混合指数模型的参数估计结果

我们采用DNML（Decomposed Normalized Maximum Likelihood）作为拟合优度的检验标准，DNML 值越低，说明拟合效果越好。所以我们可以看到当k的初值为2时，模型的拟合结果最好，其中最优结果见表2，拟合曲线见图2。

▶表2 最优DNML下的参数估计结果

▶图2 经验数据与混合指数的拟合曲线

在得到混合指数形式的损失分布函数F(x)后，进行风险曲线G(x)的构建，因为我们数据中最大损失为1972367，所以我们选取M 为2000000（假设最大可能损失等于保额），从而构造出对应的风险曲线，如图3所示。

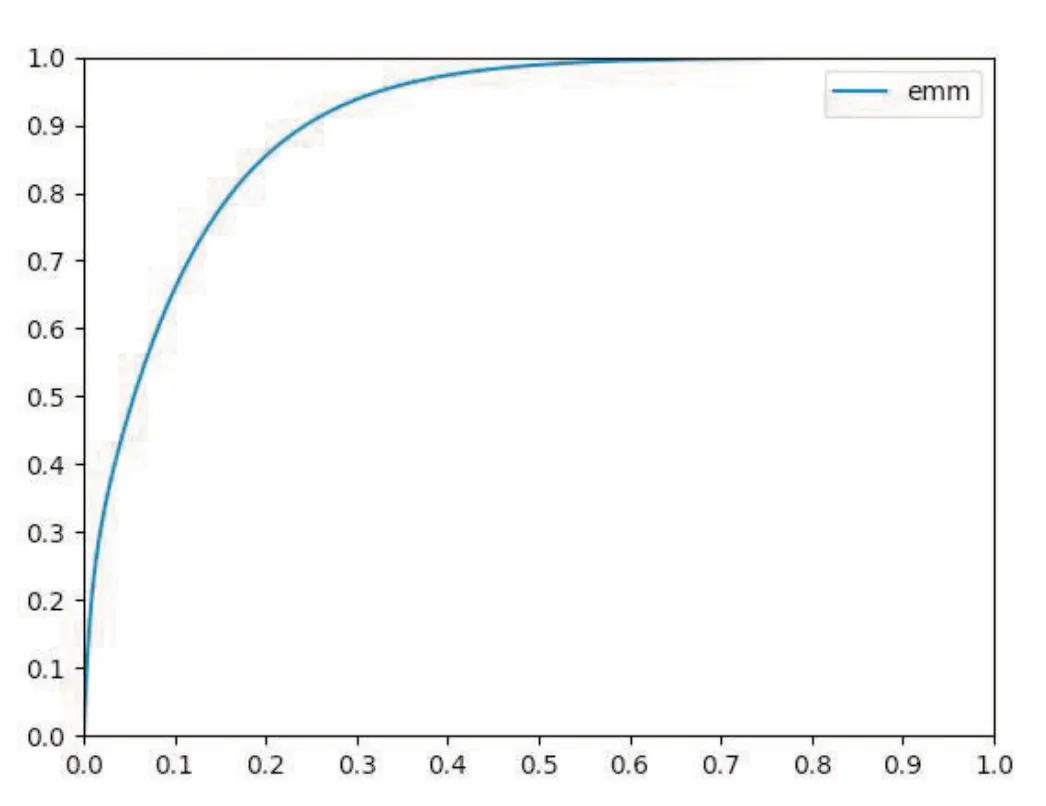
▶图3 基于混合指数模型构建的风险曲线

从图3 中，我们可以看出，绝大多数的索赔损失集中在最大损失的30%以内，其中一半以上的损失集中在最大损失的10%以内。所以仅根据此例来说，对于该责任险的免赔额定价，当免赔额为保额的10%，所收取的保费应为无免赔额情况下的40%。

五、结论

从文中图2的经验数据和混合指数的拟合曲线来看，拟合效果很好，说明混合指数模型确实比较适合保险业的损失分布，可以在实务中加以应用。而目前在美国普遍使用的是基于ISO's PSOLD方法构建的风险曲线，其采用的损失模型就是混合指数模型。这也说明基于混合指数模型的风险曲线在实务中已经具有了一定的实践意义。

但仍需注意的是，就实务中风险曲线的构建而言，对于数据的要求是比较高的。首先是需要大量的行业损失数据（比如水险、家财险、企财险）。仅靠单一保险公司很难有足够的数据量积累，所以最好是行业内的保险公司可以联合起来共同构建相应的风险曲线，在大量数据的基础上，才能使风险曲线的精度更高，从而更准确地帮助相应的定价工作。

其次是对同质性数据的筛选和处理。同一行业内部可能存在许多差异，比如对于电厂的企财险来说，火电厂和水电厂的风险就不同质，所以需要对行业小类进行区分。同时，在同一行业小类内部的很多保单也存在保额差异很大的情况，这时就要对风险曲线进行保额分段的处理，不同的保额段构建不同的风险曲线，这样可以更好地满足同质性要求。