Dispersive soliton solutions for shallow water wave system and modified Benjamin-Bona-Mahony equations via applications of mathematical methods

Asghr Ali ,Aly R.Sedwy ,

a Mathematics Department,University of Education,Lahore,Pakistan

b Mathematics Department,Faculty of Science,Taibah University,Al-Madinah Al-Munawarah,Saudi Arabia

Abstract We have utilized three novel methods,called generalized direct algebraic,modified F-expansion and improved simple equation methods to construct traveling wave solutions of the system of shallow water wave equations and modified Benjamin-Bona-Mahony equation.After substituting particular values of the parameters,different solitary wave solutions are derived from the exact traveling wave solutions.It is shown that these employed methods are more powerful tools for nonlinear wave equations.

Keywords:System of shallow water wave equations;Modified Benjamin-Bona-Mahony equation;Generalized direct algebraic method;Improved simple equation method;Modified F-expansion method;Traveling wave solutions;Solitary wave solutions.

1.Introduction

In several areas of applied science and ocean engineering investigation of traveling solutions have been played a vital role for demonstrating wave character of nonlinear problems.For plentiful expression of dilemmas in mathematical physics several nonlinear wave systems have been discussed such as the phenomena flow of heat,plasma physics and optical fibers,biology,solid state physics,chemical physics,geometry and ocean engineering [1–7].The physical phenomena and processes which take place in nature normally have intricated nonlinear features.This escorts to nonlinear mathematical models for the real processes.There is a lot interest in the practical matters involved,as well as the progress of methods to investigate the associated nonlinear mathematical problems including nonlinear wave propagation.In recent years many efficient methods have been discovered for nonlinear wave equations [8–15].These methods include such as,Homogeneous balance method,Extended tanh-function method,Jacobi elliptic function expansion method [16],Simple equation method [17–19],(G/G＇)-expansion method [20–22],Hirotas bilinear method [23],Exp function method,general projective Riccati equation method,Modified simple equation method[24],The extended direct algebraic method [25,26],auxiliary method [27]and many more [28–35].

The system of shallow water wave equations and modified Benjamin-Bona-Mahony (MBBM) equation having a fruitful applications in mathematical physics.In previous different authors used distinct techniques for constructing solitary wave solutions of these models.In authors [36]investigated solitary wave solutions of these models by extended jacobian elliptic function expansion method.Furthermore authors in Noor et al.[37]derived solutions MBBM equation via Exp-function method.But our main focus is to construct wave solutions of these models via three novel techniques.The discovered solutions are more general and powerful as previous results.The graphical demonstration 2D and 3D of some derived solutions give the basic about models knowledge to understand the physical behavior of these wave equations.Hence our employed methods are simple tools to solve nonlinear equations in applied science [38–42].

The reminant article arranged as following sections,Description of methods are in Section 2,apply proposed methods in Section 3.Discussion is in Section 4.And summary is in Section 5.

2.Description of proposed methods

Consider

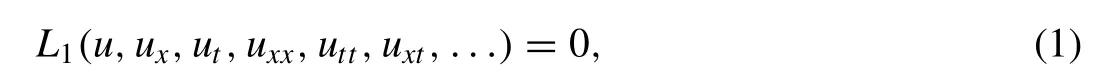
Let

Put (2) in (1),

2.1. Generalized direct algebraic method

Let solution (3) has,

SupposeΨsatisfies following,

whereβ1,β2,β3are arbitrary constants.

Put (4) with (5) in (3),attained system of collection containingk1,k2,β1,β2,β3,solving to achieve the require destination of Eq.(1).

2.2. Improved simple equation method

Let (4) has solution,

LetΨgratify,

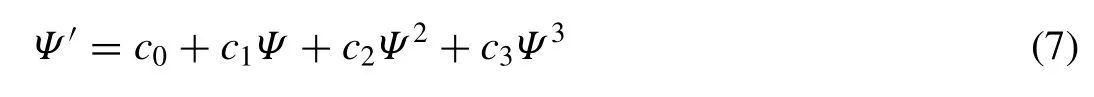
Substituting (6) along with (7) into (3).After solving obtained values of the parameters,substitute these values and solution ofΨinto (6).We obtained solution of (1).

2.3. Modified F-expansion method

Let us suppose that (3) has solution as:

LetFgratifies,

Put (8) along (9) in (3),selectA,C,BandFfrom Table1 in Aasaraai [43]and substituteaibiinto Eq.(8),completed for solution (1).

3.Applications

3.1. Application of generalized direct algebraic method

3.1.1.Thesystemoftheshallowwaterwaveequations

Let shallow water wave system [36]

Let

Putting (11) in (10),yields the following nolinear wave system as;

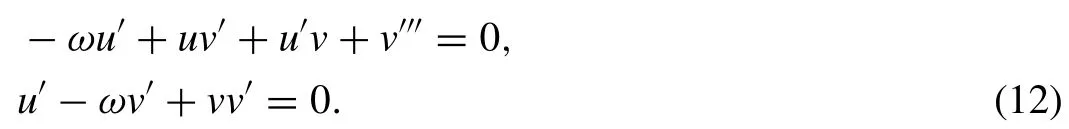
Integrating second ODE,we get

put (13) into the first equation of (12),yields

Integrating Eq.(14),

Let (15) has solution,

Put (16) along with (5) in (15),after solving,we have

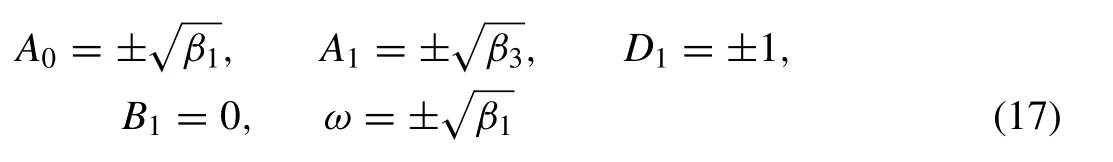
Put (17) in (16),we have

Case- I

Case- II

Case- III

3.1.2.ModifiedBenjamin-Bona-Mahonyequation

Let MBBM equation in Seadawy and El-Rashidy [36],Noor et al.[37]as;

Letu(t,x)=v(ξ),ξ=(x+kt),(21) reduce into following ODE as;

Let Eq.(16) is a solution of Eq.(22),put (16) with (5) in (22),

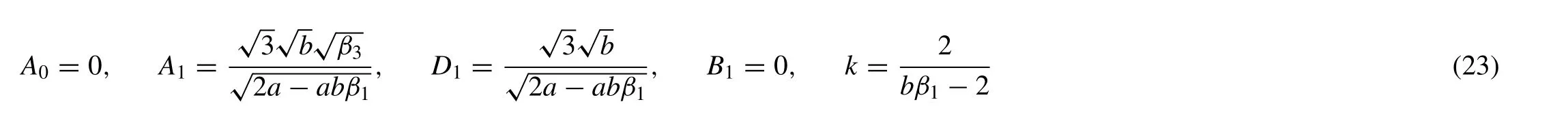
Case- I

Case- II

Case- III

3.2. Applications of improved simple equation method

3.2.1.Thesystemoftheshallowwaterwaveequations

Let (15) has solution,

Put (27) in (15) alongwith (7) and after solving obained system of equations,we have

Case I:c3=0,

Family-I

Substitute (28) in (27) with (7),yields

Family-II

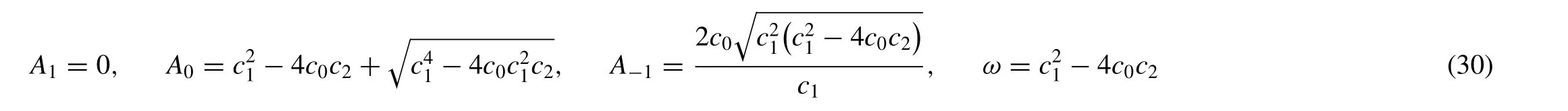
Put (30) in (27),

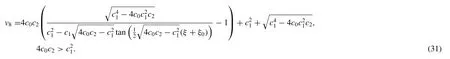
Case II:c0=c3=0,

Put (32) in (27),

Case III:c1=c3=0,

Put (35) in (27),

3.2.2.ModifiedBenjamin-Bona-Mahonyequation

Let Eq.(21) has a solutions form of Eq.(27),put (21) in (27) with (7) ;

Case I:c3=0,

Family-I

Substitute (38) in (27) with (7),yields

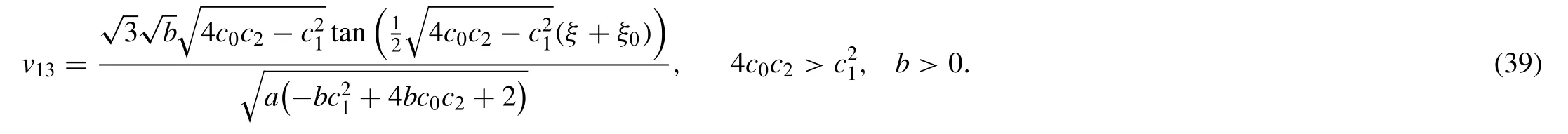
Family-II

Put (40) in (27),

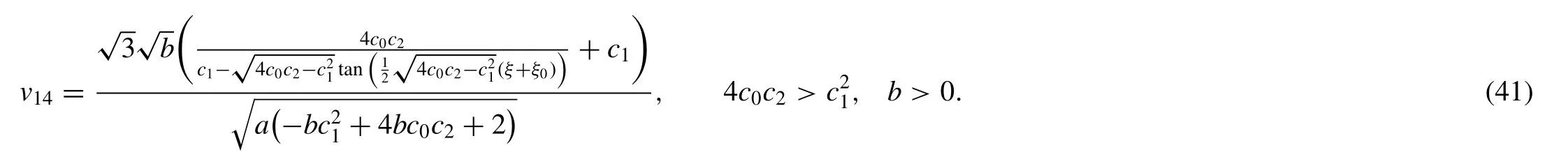
Case II:c0=c3=0,

Put (42) in (27),

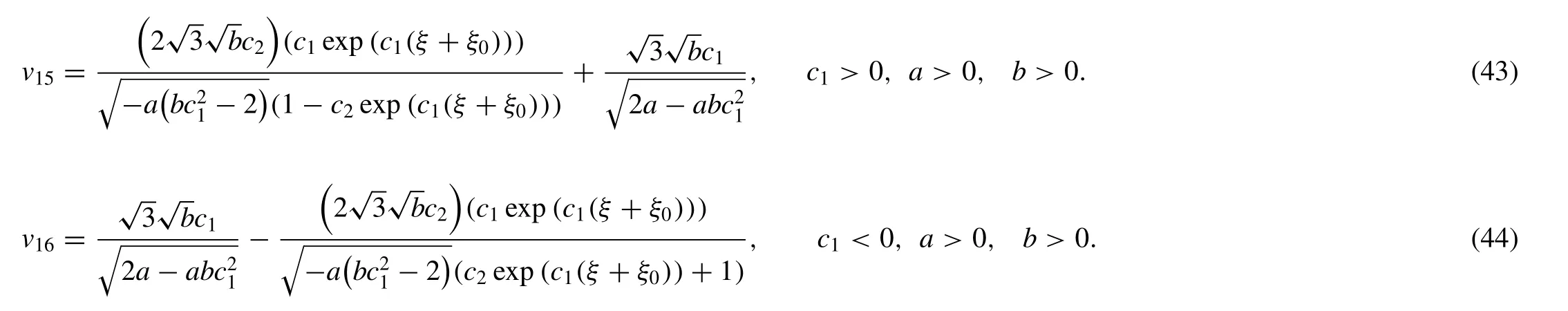
Case III:c1=c3=0,

Family-I

Put (45) in (27),

Family-II

Put (48) in (27),

Family-III

Put (51) in (27),

3.3. Applications of modified F-expansion method

3.3.1.Thesystemoftheshallowwaterwaveequations

Let solution of (15) is

Substitute (54) in (15) with (9),

ForA=0,B=1,C=−1,we have,

Put (55) in (54),

WhenA=0,B=−1,C=1,then we have,

Substitute (57) into (54),

Family-I

Put (59) in (54),

Family-II

Put (61) in (54),

Family-III

Put (63) in (54),

ForC=−1,B=0,A=1,

Family-I

Put (65) in (54),

Family-II

Put (67) in (54),

Family-III

Put (69) in (54),

Put (71) in (54),

A=

Put (73) in (54),

ForC=−1,B=0,A=−1,

Put (75) in (54),

ForA0,B0,C=0,

Put (77) in (54),

3.3.2.ModifiedBenjamin-Bona-Mahonyequation

Let Eq.(54) is a solution of Eq.(22),substitute Eq.(54) along with (9) in (22) ;

ForA=0,B=1,C=−1,we have,

Put (79) in (54),

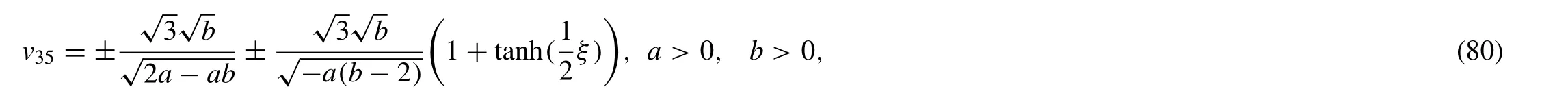
WhenA=0,B=−1,C=1,then we have,

Substitute (81) into (54),

Family-I

Put (83) in (54),

Family-II

Put (85) in (54),

Family-III

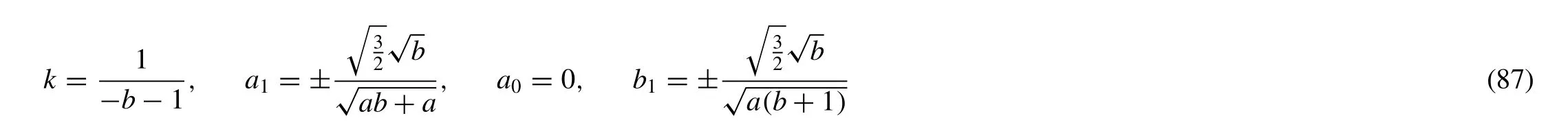
Put (87) in (54),

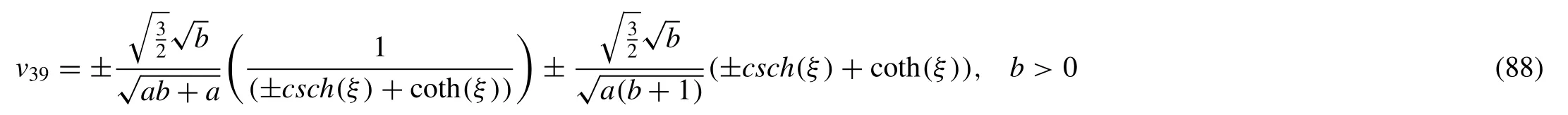
ForC=−1,B=0,A=1,

Family-I

Put (89) in (54),

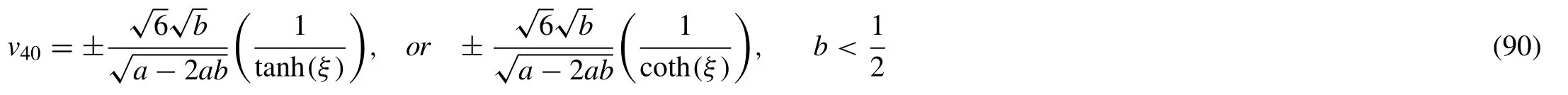
Family-II

Put (91) in (54),

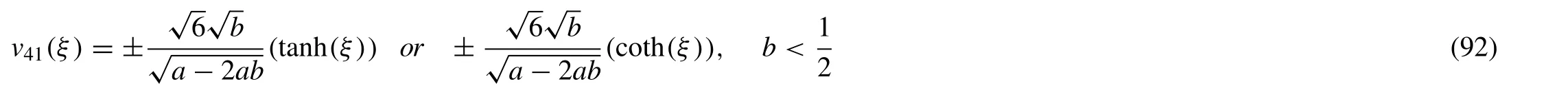
Family-III

Put (93) in (54),

Family-I

Put (95) in (54),

Family-II

Put (97) in (54),

Family-III

By putting Eq.(99) in (54),

A=

Family-I

Put (101) in (54),

Family-II

Put (103) in (54),

Family-III

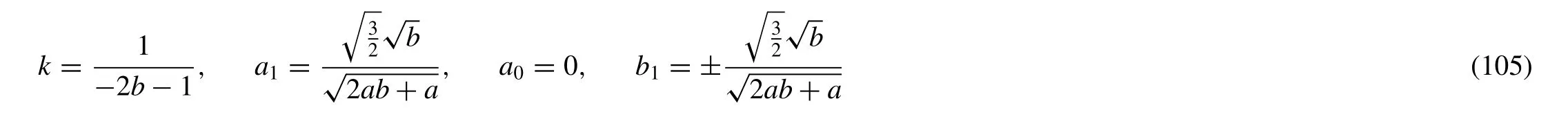
Put (105) in (54),

C=−1,B=0,A=−1,

Family-I

Put (107) in (54),

Family-II

Put (109) in (54),

Family-III

Put (111) in (54),

WhenA=0,B=0,C30,then we have,

Put (113) in (54),

Fig.1.Exact traveling waves of solution (18).

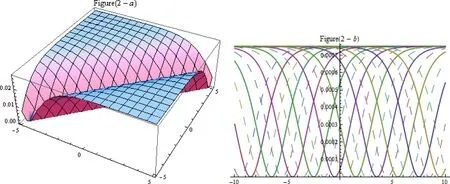
Fig.2.Exact traveling waves of solution (25).

ForB=0,C=0,Put (115) in (54),

ForA0,B0,C=0,

Put (117) in (54),

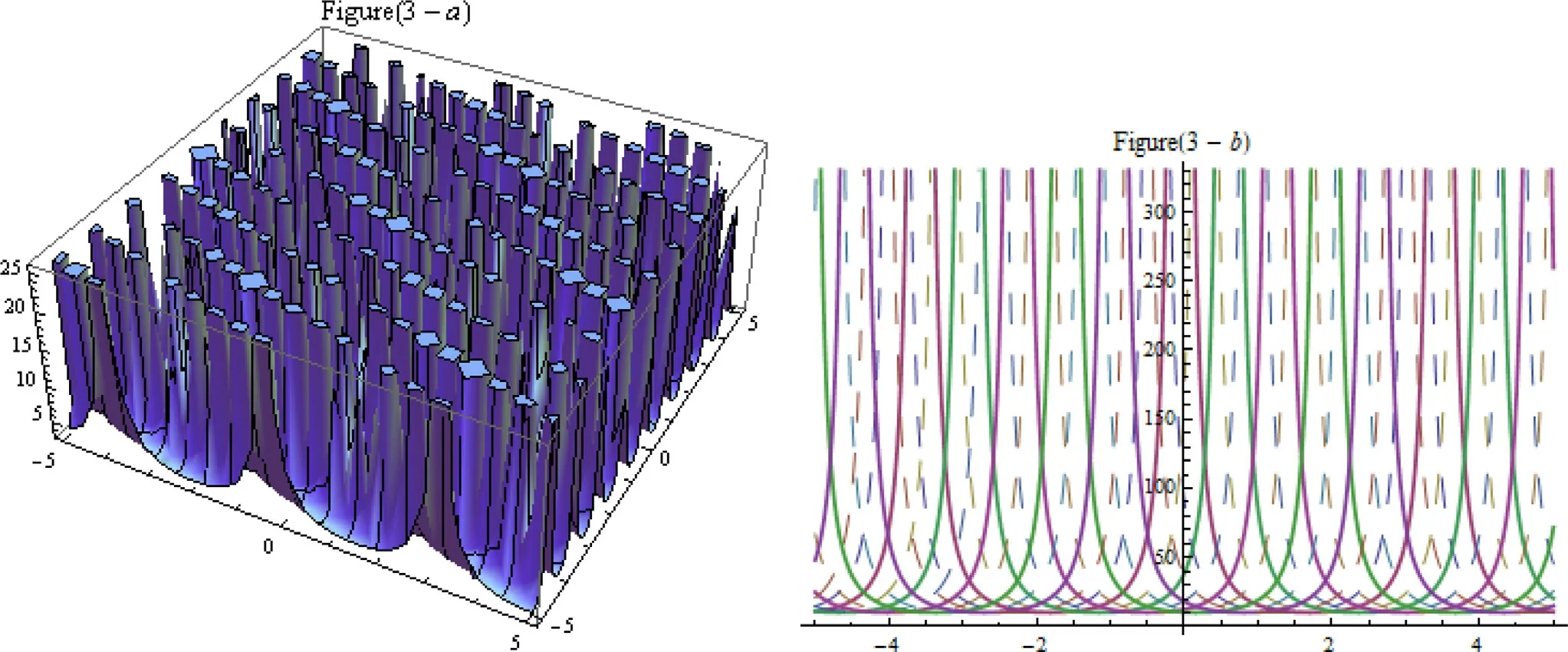
Fig.3.Exact traveling waves of solution (29).

Fig.4.Exact traveling waves of solution (34).

4.Results and discussion

Different researchers used distinct methodologies for the determination of traveling solutions of Eqs.(10) and (21) respectively [36,37].But here our central focus is to construct wave solutions of Eqs.(10) and (21) via novel three mathematical methods.By taking distinct values of parameters involve in Eqs.(4),(6) and (8) respectively,achieved several types solutions of the Eqs.(10) and (21) gradually.Moreover,our few investigated results are similar other results discussed in Seadawy and El-Rashidy [36],Noor et al.[37],Aasaraai[43],Lu et al.[44],Al-Amr [45]different researchers;

•Solutions in Eqs.(56) and (68) are likely similar form of solutions in Eqs.(32) and (30) in Seadawy and El-Rashidy[36]respectively.

•Our solutions in Eqs.(43) and (44) are approximately same form of solutions in Eqs.(19) and (26) in Noor et al.[37]respectively.

•Our solutions in Eqs.(33) and (34) are also likely form as solutions in Eqs.(39) and (38) in Aasaraai [43]respectively.

•Our solutions in Eqs.(36) and (37) are also likely form as solutions in Eqs.(40) and (41) in Lu et al.[44]gradually.

•Our solutions in Eqs.(92) and (108) are also likely form as solutions in Eqs.(26) and (27) in Al-Amr [45]gradually.

Figs.1 –6 are plotted after assigning with these particular values to the parameters such that,solutionv1atβ1=2,β2=4,β3=2,ξ0=−0.5,∊=−1 and solutionv5ata=10,β1=1,β2=4,β3=1=,b=0.005,η=1,ξ0=−0.5,∊=−1 andV7atc0=1,c1=0.9,c2=1,∊=0.5,ω=c21−4c0c2andV10atc1=−0.9,c2=0.5,∊=0.5,ω=c21andv18ata=0.05,b1=3.05,c0=1.9,c2=−0.61,∊=−0.5 andv54ata=−5,A=−1,b=10,B=−2.01 respectively.Hence from the results discussion segment and graphical representations of some solutions,we have found that our solutions are more general and powerful as compared in previous research literature.From this we found that our proposed techniques provide a best plate form as a mathematical tools for solving nonlinear wave problem in applied science.

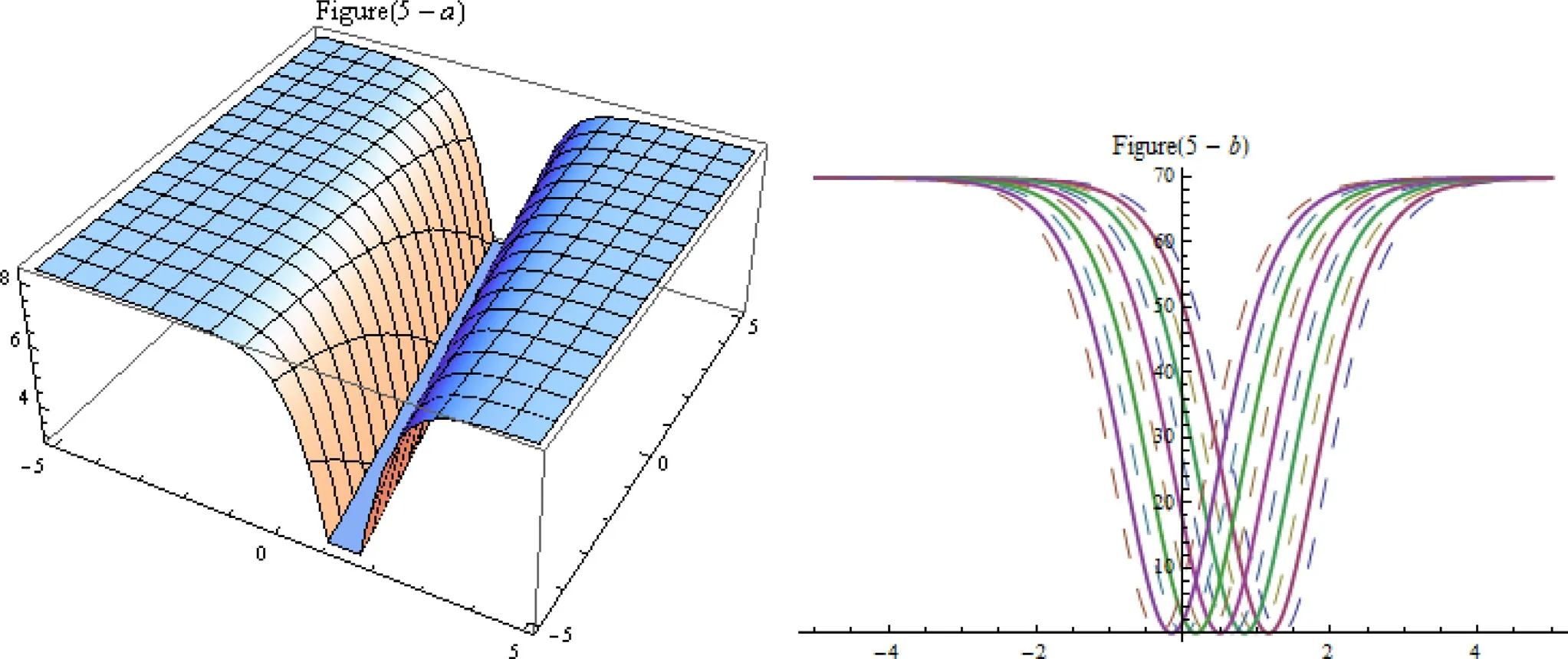
Fig.5.Exact traveling waves of solution (47).

Fig.6.Exact traveling waves of solution (118).

5.Conclusion

In this new work,three modified mathematical methods so called generalized direct algebraic,improved form of simple equation and modified F-expansion methods are utilized for the construction of the wave solutions of nonlinear wave models of system of Shellow water wave and generalized Benajamin-Bona-Mahony equations.The discovered results have fruitful applications for solving different nonlinear wave problems in the field of applied science.Hence it is shown that these employed methods powerful mathematical tool for solving several nonlinear evolution equations in applied science.

Declaration of Competing Interest

This research received no specific grant from any funding agency in the public,commercial,or not-for-profit sectors.The authors did not have any competing interests in this research.