An efficient computational technique for time-fractional modified Degasperis-Procesi equation arising in propagation of nonlinear dispersive waves

Ve Prksh Duey ,Rjnesh Kumr ,Jgev Singh ,Devenr Kumr ,

a Faculty of Mathematical and Statistical Sciences,Shri Ramswaroop Memorial University,Lucknow- Deva Road,Uttar Pradesh-225003,India

b Department of Applied Science and Humanities,Government Engineering College,Nawada,Department of Science and Technology,Bihar-805122,India

c Department of Mathematics,JECRC University,Jaipur-303905,Rajasthan,India

d Department of Mathematics,University of Rajasthan,Jaipur-302004,Rajasthan,India

Abstract In this paper,an efficient hybrid numerical scheme which is based on a joint venture of the q- homotopy analysis method and Sumudu transform is applied to investigate the time-fractional modified Degasperis-Procesi (DP) equation.The present study considers the Caputo fractional derivative.The fractional order modified DP model is very important and plays a great role in study of ocean engineering and science.The proposed scheme provides a beautiful opportunity for proper selection of the auxiliary parameter ħ and the asymptotic parameter ρ(≥1) to handle mainly the differential equations of nonlinear nature.The offered scheme produces the solution in the shape of a convergent series in a large admissible domain which is helpful to regulate the region of convergence of a series solution.The proposed work computes the approximate analytical solution of the fractional modified DP equation systematically and also presents graphically the variation of the obtained solution for diverse values of the fractional parameter β.

Keywords:Fractional Degasperis-Procesi equation;Nonlinear dispersive waves;Analytical solution;q-homotopy analysis method;Sumudu transform.

1.Introduction

Many real world problems are related with models of nonlinear nature in different areas of engineering and science,especially in physics,chemistry,biology,fluid mechanics,solid state physics,epidemiology,electrochemistry etc.A bunch of physical and scientific models,especially the problems of biology,physics,viscoelasticity,engineering and other areas are neatly interpreted by nonlinear ordinary differential equations (ODEs) and partial differential equations (PDEs) but nonlinear part of these equations creates difficulty in solution procedure and further analysis.Hence various approximate analytical schemes have been produced to handle such types of differential equations.During the past decades,exact and numerical solutions of such types of scientific systems have been determined by hiring various numerical schemes to study the nonlinear FDEs.Recentlyq-homotopy analysis transform method (q-HATM) has attracted the researchers for solution of nonlinear FDEs.This method is a beautiful copulation of theq-homotopy analysis method (q-HAM) and the Laplace transform algorithm.Theq-HAM was developed by El-Tavil et al.[ 1,2 ],which is simply a modification of the HAM with the generalization of an embedding parameter occurring in HAM.The various nonlinear problems have been investigated through theq-HAM and its various versions [3–8].The approximate scheme HAM was first developed and applied by Liao [9].Handling of many nonlinear equations using HAM shows its effectiveness and efficiency [10–13].It is notable that the HAM includes a certain auxiliary parameterfor adjustment and control of convergence region whereas theq-HAM holds an auxiliary parameteras well as an asymptotic parameterρin such a way thatq-HAM reduces to HAM forρ=1.In an earlier time,the HAM was also combined with the Laplace transform algorithm to solve various problems of nonlinear nature successfully [14–17].

The fractional differential equations (FDEs) are significant in translating the reality of nature in a very standardized way.They are actually the generalization of integer-order differential equations to model the phenomena of various fields.FDEs have acquired popularity in various areas of knowledge because they possess systems with hereditary and memory characteristics.Fractional order of a derivative provides more degrees of freedom in modeling and analysis,resulting in outputs with more accuracy,better robustness in control with greater flexibility.At present,the analysis of FDEs is a very attractive area of study in the field of applied mathematics.In recent years,many authors have been attracted towards theq-HATM to analyze the diverse nonlinear fractional models.Singh et al.[18–20]have investigated linear and nonlinear FDEs,fractional coupled Burgers’ equations,and dynamical Brusselator reaction-diffusion system representing chain of enzymatic reactions throughq-HATM for numerical solutions.In addition,q-HATM was utilized by Singh et al.[21]for an approximate solution of the fractional Rosenau-Hyman model.Kumar et al.[22]used theq-HATM for examining the regularized long-wave equation of fractional order.Kumar et al.[23]applied theq-HATM for linear and nonlinear FDEs,fractional Fitzhugh-Nagumo equation [24],and for the fractional Camassa-Holm (CH) equation [25].Recently Saad [26]utilized theq-HATM for the comparison of the Caputo,Caputo-Fabrizio and Atangana-Baleanu fractional derivatives in the context of a solution of a cubic isothermal auto-catalytic chemical system.

Some recent works related to a conformable local derivative operator and newly developed non-singular derivative operators are necessary to mention here.In 2018,Yavuz et al.[27–29]investigated the solutions of fractional Cauchy problems through theq-HAM,explored the solutions of fractional Black-Scholes equations with the Caputo-Fabrizio derivative operator,and applied homotopy techniques to FDEs with conformable local derivative operator.Sometimes ago,Yavuz[30]investigated the behaviour of two different fractional derivative operators defined with the normalized sinc function and Mittag-Leffler function for FDEs.Recently,Keten et al.[31]studied Cauchy problem involving a fractional with power kernel.In 2016,Gomez-Aguilar et al.[32]investigated the fractional Liénard type model of a pipeline with the fractional derivative without singular kernel.In continuity,Yépez-Martínez et al.[33]applied Feng’s first integral method to the nonlinear mKdV space-time fractional equation fractional.In 2017,fractional order evolution equations were examined by Morales-Delgado et al.[34]in a proper way.In 2018,Yépez-Martínez et al.[ 35,36 ]applied the sub-equation method and first integral method,respectively,for the Hirota-Satsuma coupled KdV equation and nonlinear differential equations with conformable derivatives.Optical solutions of the Ginzburg-Landau equation were explored by Ghanbari et al.[37].Recently,a new modified definition of Caputo-Fabrizio fractional derivative has been developed and applied to multi-step HAM by Yépez et al.[38].In continuation,Yépez et al.[ 39,40 ]have examined the resonance nonlinear Schröndinger type equation and the Lakshmanan-Porsezian-Daniel equation for optical solutions by incorporating Atangana’s conformable derivative and M-derivative respectively.

Recently,optical and complex soliton solutions for various physical models have been founded and studied by many authors.In 2020,Gao et al.[41–43]studied and analyzed,respectively,the new complex wave patterns to the electrical transmission line model,optical solitons in the cubic-quartic nonlinear Schröndinger equation,and complex solitons in the conformable (2 + 1)-dimensional Ablowitz-Kaup-Newell-Segur equation.In this sequence,instability modulation for the (2 + 1)-dimension paraxial wave equation and its new optical soliton solutions in Kerr media were investigated by Gao et al.[44].In 2019,Gao et al.[45]investigated the fractional Drinfeld-Sokolov-Wilson equation with Mittag-Leffler law usingq-HATM.In 2019,Al-Ghafri et al.[46]investigated soliton and other solutions for (3 + 1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation.

This paper considers the nonlinear time-fractional modified Degasperis-Procesi (DP) equation arising in modeling of propagation of nonlinear dispersive waves.The DP equation was first recognized by Degasperis and Procesi [47]in 1999 during a search for asymptotically integrable PDEs.It has been found that the DP equation exhibits the same role in a water wave theory as the CH equation due to its mathematical characteristics.It is notable that the DP equation is a bi-Hamiltonian system and provides interesting wave solutions [48].Actually the DP equation is a nonlinear PDE which helps in modeling of nonlinear dispersive waves and it can be solved through the techniques of soliton theory.The DP equation arises in modeling of two-dimensional water wave propagation [49–51].The DP equation is a centre of attraction for researchers in the context of two main aspects.First aspect is its characteristic of integrability and other is its abounding nonlinear anomaly because of the coexistence of nonlinear convection and dispersions.There are various physical phenomena that are generated due to nonlinearity in dispersive waves.There are numerous examples of ocean water waves which are nonlinear dispersive by nature.In shallow water,the linearization of the equations imposes much more severe conditions on the wave amplitude than it does in deep water,and nonlinear effects are stronger and more easily observed.Under the influence of gravity,water waves with a longer wavelength progress faster than those with a shorter wavelength.It has been observed that internal gravity waves(IGWs) in the deep-ocean demonstrate dispersion relation between constant stability frequencies with wave frequency because of directionality of gravitational restoring force.Note that,in dispersive waves,the speed of propagation of an infinitesimal disturbance depends on the wave numberk.Moreover,it had already been shown that a strong nonlinearity exists in progressive deep-ocean gravity waves.The crest and trough profile were observed to be distorted having sharper crests in contrast to troughs;and the phase speedcwas found to increase to some extent with increasing slope as given in work of Phillips [52]aswherekspecifies the wave number,athe amplitude,andgthe acceleration due to gravity.The wave frequency does not vary directly with wave number,and the group velocity is not equal to the phase velocity.The dispersion relation for surface waves is amplitude dependent.Different wave components go through resonant interactions and exchange of energy takes place among them,so that the propagation of energy in the physical arena bears constant redistribution.Resonant interactions and amplitude dispersion are two expressions of this mutual activity between nonlinear effect and those of dispersion,yet the miscellaneous physical phenomena with which they are linked are impressive [52].

Non-resonant second-order interactions in surface waves perform an important role in many oceanographic approaches.It is a well-known fact that nonlinear waves are neatly described by nonlinear equations,and therefore the superposition principle does not generally apply.This means that nonlinear wave equations are more difficult regarding mathematical analysis,and no general analytical technique exists for their solution.In the light of these facts,it may be inferred that nonlinear internal waves are often observed in the ocean and it may be useful if simplified evolution equations may be effectively applied to illustrate strongly nonlinear dispersive waves in different areas of the ocean science and engineering.

Nonlinear nature of dispersive waves characterize the characteristics of wave-wave interactions,capillary-gravity waves,internal gravity waves (which are common in both the ocean and the atmosphere),and surface waves.In this direction,nonlinear time-fractional CH and DP equations have proved their usefulness regarding these types of analysis in respect of oceanographic science and engineering.In 1993,Camassa and Holm [53]derived a new totally integrable dispersive shallow water equation that is bi-Hamiltonian and thus possesses an infinite number of conservation laws in involution.This equation was constructed by utilizing an asymptotic expansion directly in the Hamiltonian for Euler’s equations in the shallow water regime.Completely integrable nonlinear PDEs occur at various levels of approximation in shallow water wave theory.Such equations carry soliton solutions-spatially localized coherent structures that interact nonlinearly among themselves then remerge,retaining their identity and depicting particlelike scattering behaviour.Nonlinear and third-order dispersive DP equation is also considered as a model for shallow water dynamics and its asymptotic correctness tallies as for the CH equation [54].Nonlinear time-fractional CH and DP equations model the unidirectional propagation of two-dimensional shallow water waves over a flat bottom and can be easily solvable by techniques of soliton theory.The solitary waves of the CH and DP equations are stable solitons with a peak at their crest [55].In the ocean,the gravity waves generated by wind are random and resonant interactions among the diverse wave components that procure a slow and systematic redistri-

where b is a positive integer.

Helal et al.[62],Wazwaz [63],Seadway [64],and Liu[65]studied the modified form of DP equation.Wazwaz[63]established and studied the generalized modified CH and DP equations for the first time.The dimensionless form of the general modified DP and CH equation is given by

where a is a positive integer.

Clearly the nonlinear convection term has been transformed tov2vη.Wazwaz [63]founded these modifications of the DP equation as a tool to discover the variation in the physical pattern of the generated solution.It is notable that there exist multi-peakon solutions for the standard DP equation.But the characteristics of these peakon solutions are transformed to the bell-shaped solitons in case of the modified DP equation.This equation is relevant and helpful in analyzing the shallow water dynamics and is integrable.It has already been proved that all the equations in this family have peakon and multipeakon solutions.Many analytical schemes have been applied to analyze this family of equations.However,the solitary wave solutions of these generalized modified DP and CH equations were first founded by Wazwaz [61]in 2006.The above-mentioned generalb- Eq.(1) reduces to the DP equation forb=3 as follows:bution of energy among components with different directions and wave number magnitudes.

In nature,nonlinear solitary waves (i.e.solitons) most commonly exist in the form of IGWs in the ocean where the internal solitons are practically significant.Nonlinear IGWs are generated by tidal currents in deeper regions [56].The internal gravity waves are not just nonlinear but strongly nonlinear in the sense that their propagation velocity can remarkably differ from that of linear waves known by early observations provided by Halpern [57].In the past two decades,strongly nonlinear IGWs were studied by various researchers in many coastal areas and deep areas of the ocean.Ostrovsky et al.[ 58,59 ]described the strong internal waves in coastal areas and also derived evolution equations for strongly nonlinear internal waves.There are various aspects of study of the DP equation which are clearly related to the practical approaches towards ocean engineering and science.DP equation depicts blow-up phenomenon and infinite propagation speed also.The DP equation is well-known to model important nonlinear effects such as wave breaking and shock creation.In 2007,Lundmark [60]analyzed the formation and dynamics of shock waves in the DP equation.Thus,the fractional DP model and its solution are very important and useful in study of ocean engineering and science.

A significant physical model known asb-equation studied by Wazwaz [61]is described as follows:which is known as the modified DP equation.Wazwaz[63]derived the solutions of the modified Camassa-Holm equation as well as the modified DP equation by implementing the extended tanh scheme.

The exact solution of the modified DP Eq.(3) obtained by Wazwaz [61]is given as follows:

The key objective of this study is to compute the approximate solution of the following time-fractional modified DP equation as given below:

with the initial condition:

in dimensionless space-time variables (η,ω),wheresignifies the Caputo fractional derivative (CFD) of orderβ.

In the last decade,many researchers applied the several semi-analytical techniques,for instance,the applied integral bifurcation scheme [66],wavelet optimized finite difference method [67],homotopy perturbation scheme [68],Adomian decomposition scheme [69],variational iteration scheme [70–72]and Exp-function method [73]for solving the nonlinear modified DP and CH equations.Baskonus et al.[74]applied the natural transform decomposition method and Zada et al.[75]investigated the modified DP equation through the optimal asymptotic scheme.More recently,modified forms of CH and DP equations were investigated via quartic B-spline collocation finite difference scheme [76].Gupta et al.[77]have used the homotopy perturbation method (HPM) for the approximate solution of time-fractional CH,modified CH and DP equations.In 2016,the modified DP equation was also investigated by Chen [78]in the context of stability.

The present work shows the application of the hybrid schemeq-homotopy analysis Sumudu transform method (q-HASTM) to study the modified Degasperis-Procesi equation with time-fractional derivative.The present hybrid schemeq-HASTM established by Singh et al.[79]was utilized to analyze the fractional model concerning the interpersonal relationships.This method is a copulation ofq-HAM,homotopy polynomials and Sumudu transform algorithm.It is notable that the fusion ofq-HAM with Sumudu transform provides a time-saving result.The rest of the study is composed in the subsequent way:In Section 2,the elemental concepts and formulae regarding the fractional calculus and Sumudu transform operator are provided.In Section 3,the fundamental computational approach ofq-HASTM is given.Section 4 extends the application ofq-HASTM for solving the DP equation with Caputo time-fractional derivative.Section 5 discusses the various numerical simulations and graphical analysis for the fractional modified DP equation.Finally,Section 6 concludes the study.

2.Preliminaries and notations

This part describes the elemental formulae of fractional derivatives and integrals along with the definition and properties of the Sumudu transform (ST) operator.

Definition 1.[80]A real valued functionh(ω),ω＞0 is said to be in the spaceCλ,λ∈ ℜ if ∃ a real numberω＞λsuch thath(ωτ)=τωh1(ω),whereh1∈C[0,∞) and exist in the space

Definition 2.[80]The Caputo fractional derivative (CFD) ofh(ω) of orderα(α≥0) is defined as

whereDξsignifies the classical derivative of orderξ.

For the CFD operator,we have

Definition 3.[80]The fractional integral operatorJβof orderβ(β ＞0) of a functionh∈Cℓ,ℓ≥−1 in Riemann-Liouville(RL) sense is described by

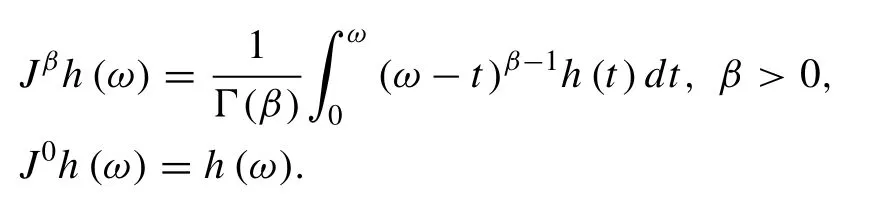
For the RL integral operator,we have

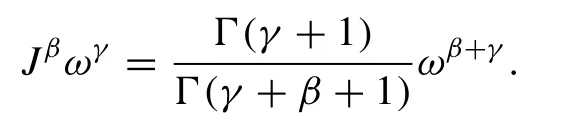
Definition 4.[80]The CFD operator ofh(η,ω) of orderα ＞0 is defined as

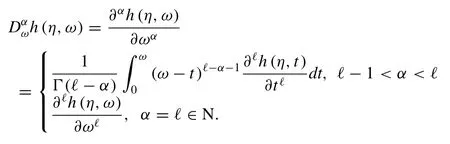
Definition 5.The ST operator presented by Watugala [81]is defined over the set of functions as follows:

by the following formula

Definition 6.[82]The ST of the CFD operatorDαωh(η,ω)is written as

In order to see more details and properties of ST,see the work conducted by Belgacem et al.[ 83,84 ].

3.Computational procedure of the q -HASTM

To elucidate the basic working steps of the offered schemeq-HASTM for fractional PDEs,the ensuing general nonlinear non-homogeneous fractional order PDE is considered as given below:

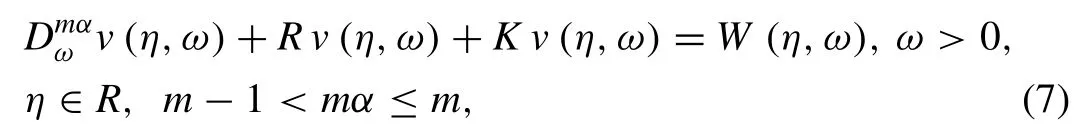
Now the computational approach suggests the implementation of Sumudu transform (ST) operator on Eq.(7),which delivers

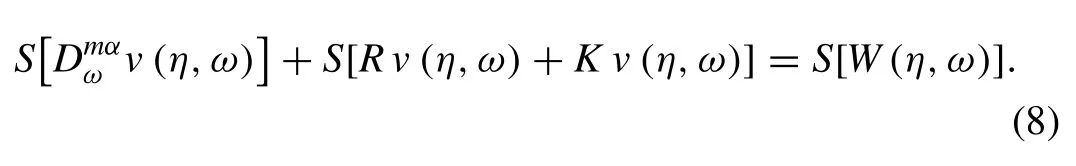
Now the operation of formula of Sumudu transform for fractional derivative in Eq.(8) provides

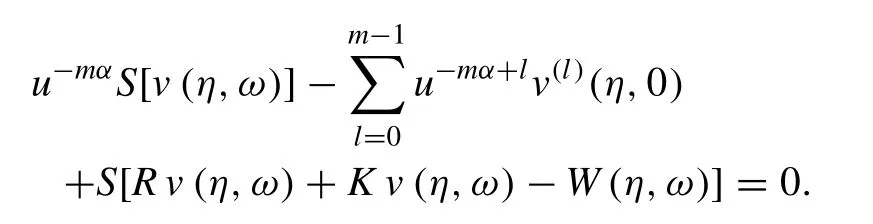
After simplification,we get

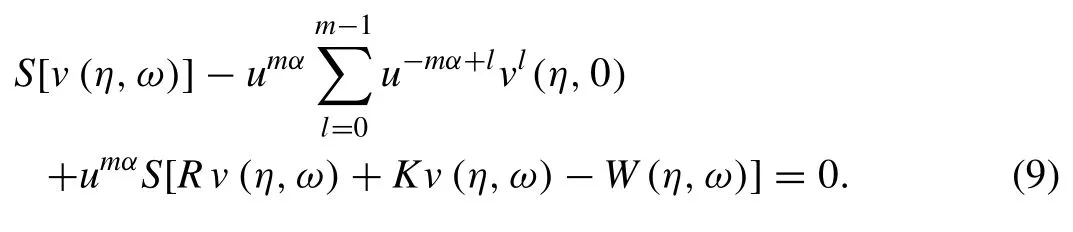
Now the nonlinear operator is constructed as follows:

Now the linear operatorζis picked as:

ζ[φ(η,ω;q)]=S[φ(η,ω;q)]with the characteristicζ[p]=0 for a random constantp.

Now the homotopy can be constructed in this way:

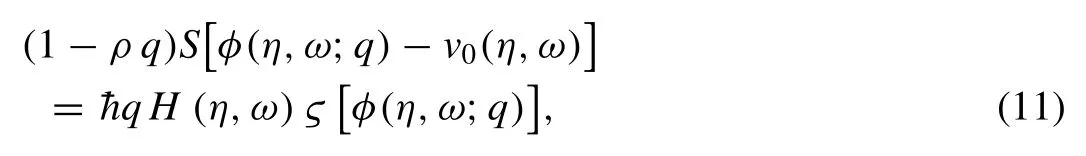
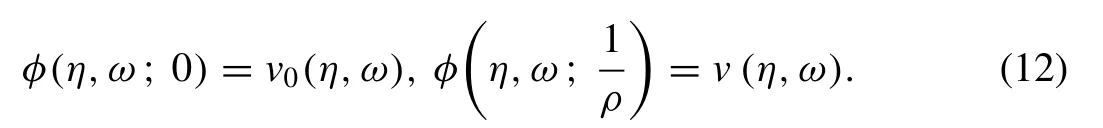
Hence whenqvaries from 0 tothe solution deviates fromv0(η,ω) tov(η,ω).Now a Taylor’s series expansion of the functionφ(η,ω;q) about q yields the following series:

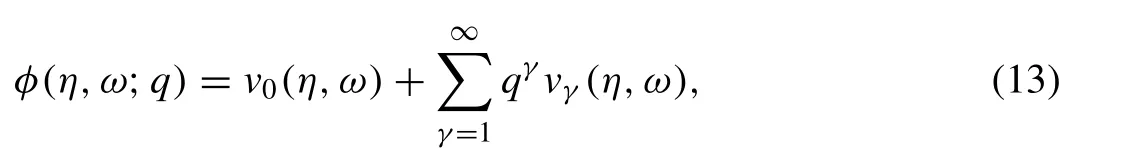
where

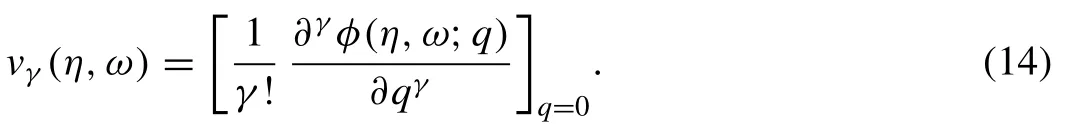
The non-zero auxiliary parameterregulates the convergence domain of the series solution (13).Therefore the series represented by Eq.(13) converges atq=by means of the suitable choice of auxiliary linear operator,the initial guessv0(η,ω),ρ,andH(η,ω).

Thus we have

The above-mentioned Eq.(15) establishes a relationship betweenv0(η,ω) and the exact solutionv(η,ω) through the termsvγ(η,ω)(γ=1,2,3,...)which are still to be computed.Eq.(15) provides the approximate series solution of the concerned Eq.(7).

Now we define the vectors as follows:

For computation of theγ th-order deformation equation,the zeroth-order deformation Eq.(11) is differentiatedγ-times w.r.t.qand then choosingq=0 and dividing them finally byγ! provides theγ th-order deformation equation as follows:

Operating the inverse Sumudu transformS−1on the aboveobtainedγ th-order deformation Eq.(16) andH(η,ω) is taken as 1,we have

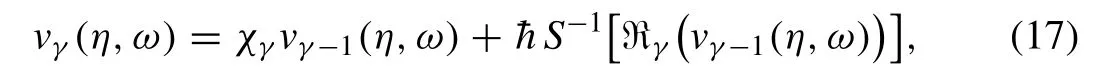
where

In Eq.(17),the value of ℜγ(vγ−1(η,ω))is expressed in a novel fashion as

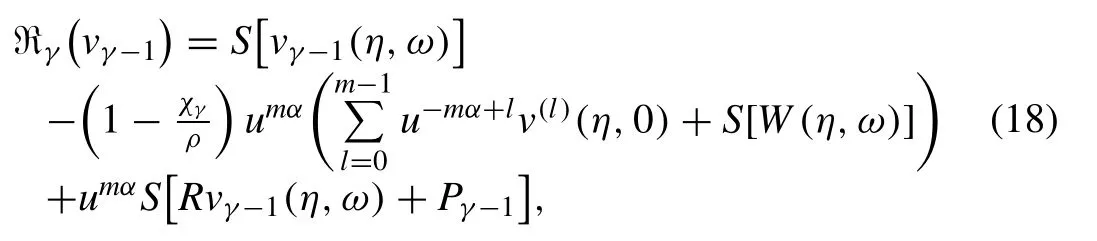
In Eq.(18),Pγdenotes the homotopy polynomial introduced by Odibat and Bataineh [85]in computational procedure ofq-HASAM and is expressed as given below:

andφ=φ0+qφ1+q2φ2+q3φ3+....

Putting the value from Eq.(18) in Eq.(17),we get

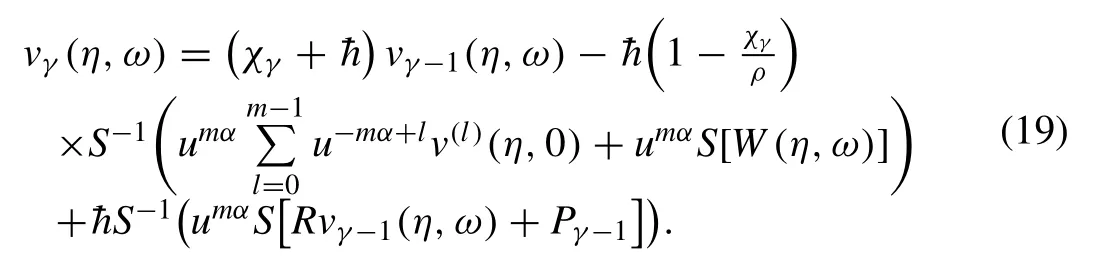
Now,the computation of various components of series solution can be done in a very straightforward manner and the final structure of q-HASTM solution is expressed as

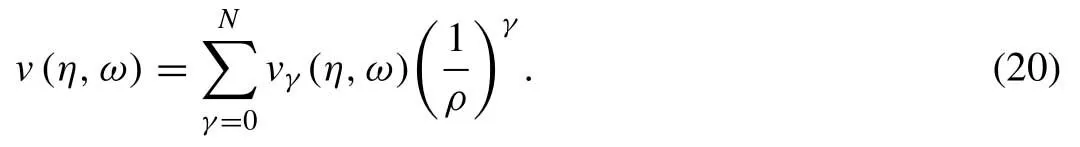
WhenN→ ∞,we acquire a precise approximation of the solution of given PDE (7).It is notable that theq-HASTM reduces to HASTM forρ=1.Robustness measures reliability of a semi-analytical technique that means results computed through the technique are found to be authentic even in a slightly varying condition.Actually it indicates the ability of a technique to always remain unchanged in respect of marginal changes.The robustness of such kind of series solutions has already been shown.

4.q -HASTM solution of the fractional modified Degasperis-Procesi equation

This part extends the implementation ofq-HASTM for the fractional modified DP equation of orderβgiven as follows:

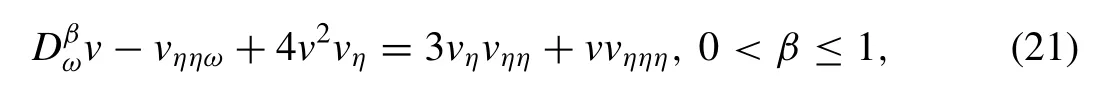
with the given condition:

The initial approximation is as follows

The exact solution of Eq.(21) forβ=1 is provided by

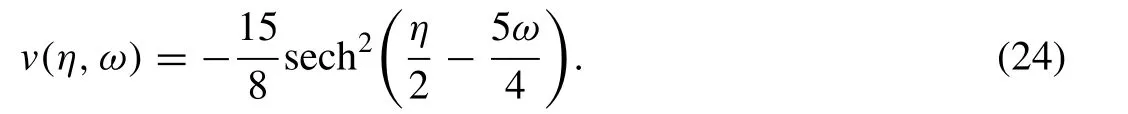
Thus the initial approximation is given by

Now the operation of ST operator on Eq.(21) along with the implementation of the formula of the Sumudu transform for fractional derivative imparts

After simplification,we get

Using the initial condition (22) and further simplification yields

Now the nonlinear operator is structured as follows:

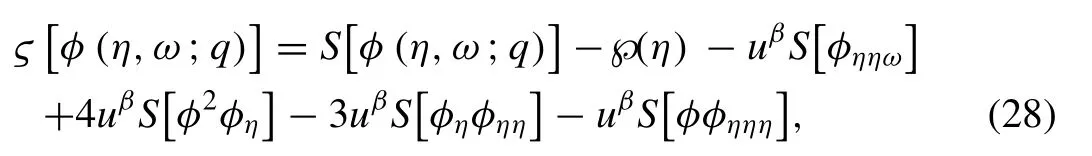
Now the suitable form of the linear operator can be selected as follows:

ℑ [φ(η,ω;q)]=S[φ(η,ω;q)],with ℑ [a]=0 for a random constanta.

By utilizing theq-HAM along with the underlying hypothesisH(η,ω)=1,the deformation equation of zeroth order is built as follows:

For the embedding parameterq=0 &q=these subsequent expressions hold well as follows:

Hence,with the variation ofqfrom 0 tothe solution deviates fromv0(η,ω) to the solutionv(η,ω).

Theγ th-order deformation equation is computed as follows:

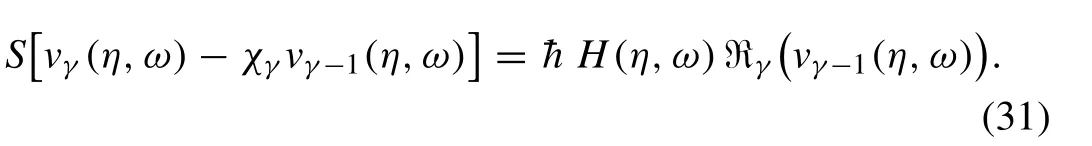
Now operating the inverse ST operatorS−1on Eq.(31) and takingH(η,ω) as 1,we have

where

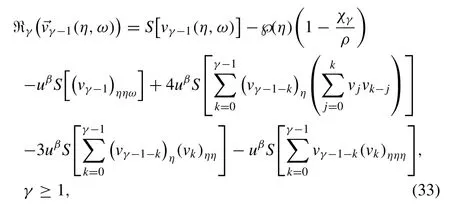
Now the solution of theγ th-order deformation Eq.(31) is provided by

Now by utilizing the generated iterative scheme (34) and the associated initial condition (23),the different iterative terms are computed as follows:

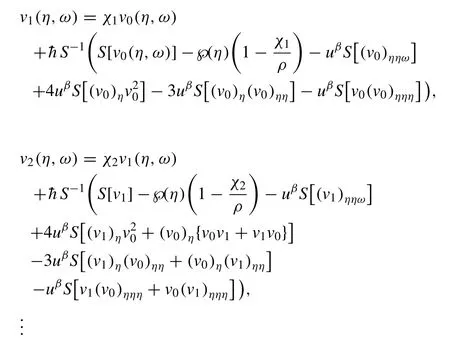
After simplification,we get

Working in the same fashion,the rest of the values ofvγ(η,ω) forγ≥3 can be readily calculated and hence the overall series solution is fully acquired.Thus the solution of Eq.(21) obtained throughq-HASTM in a series shape is constituted in the following way:

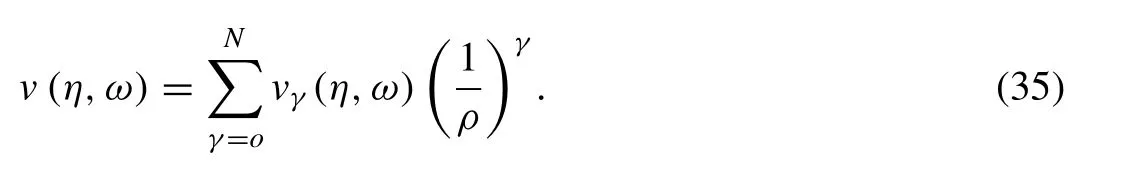
ForN→ ∞,a precise approximation of the solution of time-fractional modified DP equation is acquired.

The approximate analytical solution of the given modified fractional DP equation obtained viaq-HASTM is in a good correspondence with the results obtained via optimal homotopy asymptotic method (OHAM) [75],HPM [77]and variational HPM [86].The other methods andq-HASTM give accurate solutions butq-HASTM has a larger domain of convergence and greater flexibility as compared to other methods.

The eminence of theq-HASTM lies in its capability to unite two robust computational schemes to investigate nonlinear FDEs.The fusion of the semi-analytical schemeq-HAM with an appropriate integral transform such as Sumudu transform lessens the time factor in searching for a solution to the nonlinear problem.Additionally,theq-HASTM does not demand linearization,discretization or any other restrictive assumption.It depicts small perturbations,lessens mathematical calculations notably,introduces non-local effects,and does not involve complicated polynomials or integrations.Theq-HASTM shows an improvement ofq∈ [0,1]in HASTM toThe occurrence of the termin the obtained solution provides faster convergence as compared to the standard HASTM.The convergence of theq-HASTM solution can be adjusted and controlled through the auxiliary parameter ħ and the asymptotic parameterρ.

5.Numerical simulation and discussion

This part of study analyzes the individual impact of the fractional orderβon the functionv(η,ω).The numerical investigation of the fractional Degasperis-Procesi equation through the utilization ofq-HASTM considers various specific values ofβ.The approximate results ofv(η,ω) are evaluated for varied fractional Brownian motionsβ=0.75,0.50,.25&also for the classical motionβ=1 and the numerical outputs are demonstrated by means of three-dimensional Figs.1–3 and two-dimensional Fig.4.The analysis shows the continuous dependency of obtained numerical solutions on the fractional parameterβ.It can be easily concluded that as the value ofβreaches to 1,the numerical solution of the fractional modified DP equation tends to the exact solution.

Fig.1.Variation of v (η,ω) vs.ω and η for β=1.

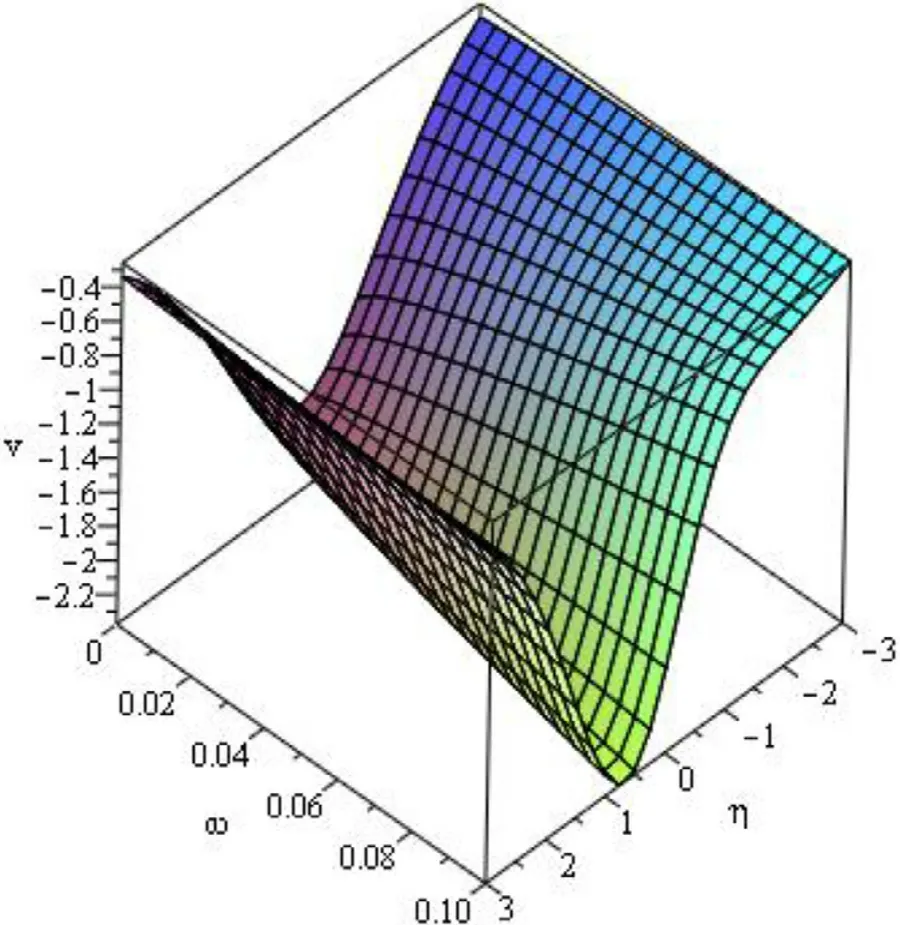
Fig.2.Variation of v (η,ω) vs.ω and η for β=0. 75.

The three-dimensional Fig.1 ofv(η,ω) for small time domainωand for −3 ≤η≤3 depicts the nature of the solutionv(η,ω) forβ=1.In the same way,the variations ofv(η,ω) forβ=0.75,0.50 respectively with the increasing value ofω&ηcan also be explained through Figs.2–3.The two-dimensional plot ofv(η,ω) is presented in Fig.4 for 0 ≤ω≤2,η=0.1 and for various values ofβ.The accuracy of the numerical solution of the DP equation ensures effectiveness of this hybrid mathematical scheme for solving the fractional nonlinear modified DP equation.By means of an additional number of evaluated terms ofq-HASTM,one can get the numerical result with higher accuracy.The numerical results exhibited in the form of graphs prove efficiency and accuracy of the hired scheme.Thus the offered scheme is highly logical and deserves to study various nonlinear fractional-order mathematical models occurring in the real world.

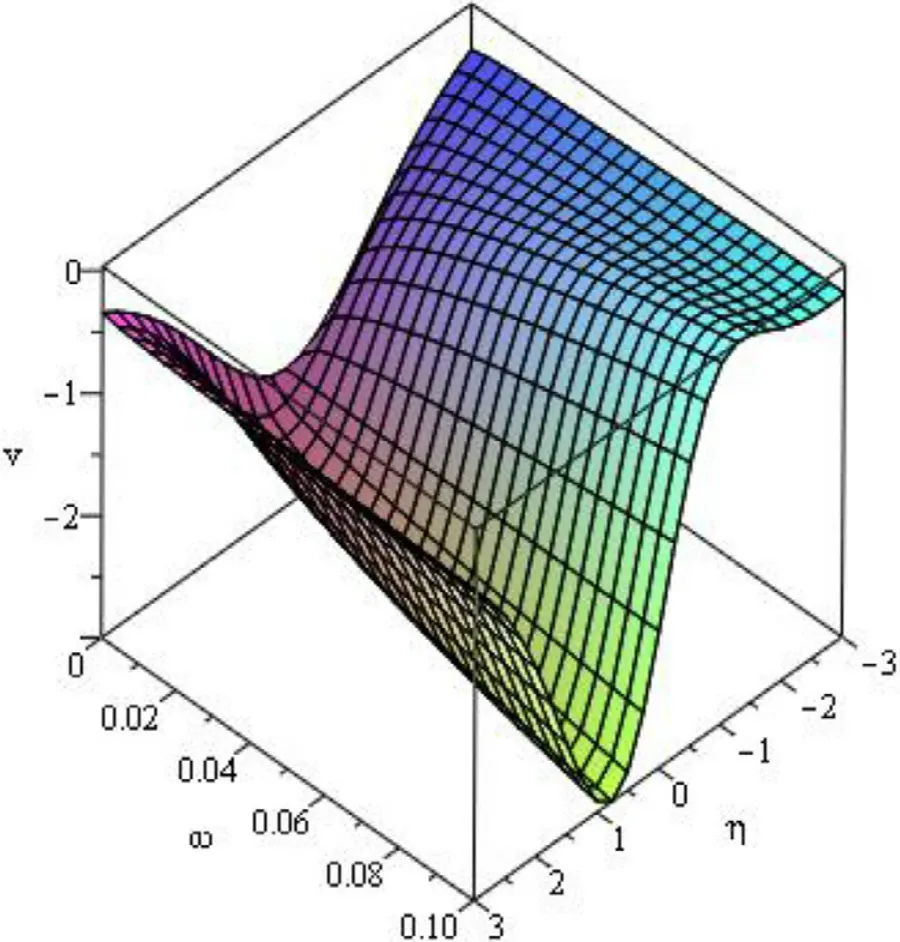
Fig.3.Variation of v (η,ω) vs.ω and η for β=0. 50.

Fig.4.Plots of v (η,ω) vs.ω for η=0. 1.

6.Concluding remarks

In the present study,a numerical approachq-HASTM has been utilized to study the modified Degasperis-Procesi equation with time-fractional derivatives.The results indicate that theq-HASTM solution is more general than the other numerical schemes such as HPM,HAM,q-HAM,and HASTM and includes their results as a specific case.The two- and three-dimensional plots ofv(η,ω) show their variations with respect to timeωand the fractional parameterβ.The capability and accuracy of the proposed method reflects from its high-capacity to offer the large convergence region for the solution via auxiliary parameters ħ and the asymptotic parameterρ(≥1).Thus the present method is much capable and systematic in the context of computational procedure and can be utilized to solve the various nonlinear FDEs representing real phenomena of various streams in a very efficient manner.There are various methods in an available literature that have been used to investigate the above-mentioned modified DP equation.The literature review regarding this has already been provided in an introduction section.But a newly developedq-HASTM has never been used to investigate the fractional modified DP equation.The novelty of the present paper lies in smooth implementation ofq-HASTM to the fractional modified DP equation along with depiction of variation of numerical results regarding various values of the fractional orderβ.The proposed work is related to the modeling of the modified DP equation with Caputo fractional derivative operator.However,the Riemann-Liouville derivative operator has been utilized frequently in analysis of FDEs.But various applied problems generally require fractional derivatives of proper form,for instance,the Caputo derivative which provides initial conditions with clear interpretations for FDEs.This fact enhances the applicability of the CFD operator as compared to the RL version.As a future scope,theq-HASTM can also be implemented to study and investigate the recently introduced complex and highly nonlinear fractional-order models with newly developed fractional operators arising in ocean science and engineering.

Declaration of Competing Interest

The authors declare that there is no conflict of interests regarding the publication of this paper.