浅谈工业机器人柔性系统的故障诊断

德州职业技术学院 黄 克

工业机器人作为柔性制造系统的关键部分，在日常运行中易出故障，此种故障非常隐蔽不易被发现，这一特点导致柔性制造系统难以普及并广泛应用。本文采用了故障树分析法和Petri网理论相结合的方式，并借助工业机器人故障的关联矩阵，可以明确找出故障传播路径，发现工业机器人的故障位置，以便最大程度缩短寻找故障点的时间。

柔性制造系统，即“Flexible Manufacturing System”（FMS），将其应用到工业生产中，有助于提升生产效率、缩短生产周期，最大程度上减少生产成本，同时保证产品质量。因此，柔性制造系统在一定领域内得到了使用。在柔性制造系统中包含了物料系统、加工系统、计算机控制系统等。在加工系统、物料系统中，工业机器人作为其中重要组成部分，如果发生故障，则会直接影响到柔性制造系统的正常运行，影响企业正常生产。所以，需要明确工业机器人故障位置并加以有效解决，从而全面提升工业机器人在柔性制造系统中的工作效率，促进生产。

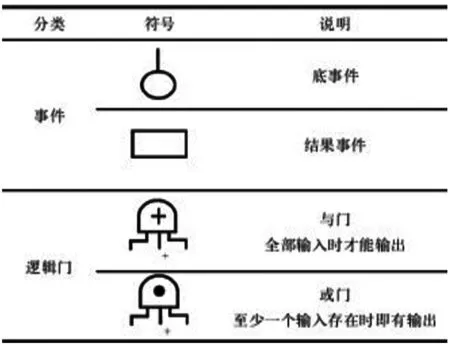
图1 故障树部分元件图

1 故障树分析法与Petri网模型

故障树分析法（Fault Tree Analysis，FTA）属于一种系统分析方法，其最大的特点就是逻辑性强，其主要针对系统中出现的不确定信息进行处理，图1为故障树部分元件。而建立在Petri网模型上的系统故障诊断方法，在诊断推理、表达逻辑关系方面展现出较强的能力。融合故障树分析法、Petri网模型有助于提升故障诊断效率，进而实现降低成本的目的。本文融合了故障树分析法和Petri网模型，全面分析工业机器人运行过程中容易出现的故障，在此基础上，模拟出相应的故障传播路径，希望通过运用此种方法，可以更加高效的找出工业机器人故障排除方法，为后续故障维修工作提供支持。

2 关联矩阵

为有效解决故障传播问题还可以运用关联矩阵，从而有效诊断故障问题，图2是故障诊断分析流程图，本文按照此流程对工业机器人的故障进行分析。首要任务就是构建出相应的故障树，这就需要搜集相关信息并查阅有关的资料，为构建故障树提供支持。与此同时，在目前故障树模型基础上，构建出工机器人故障的Petri网模型，通过故障关联矩阵的作用模拟出一个故障传播路径；最后，计算并对该传播路径进行验证。

图2 故障诊断分析流程

Petri网在描述模型结构时可以运用矩阵运算方法实施。Σ=（P，T，F，M0）将其设定为有限P/T网，而基网N=（P，T，F）是纯网，P×T→C被称为Σ的关联矩阵。如果XT是T→P输出矩阵的转置矩阵，则Y是输入矩阵，也就是P→T的矩阵，此时在XT和Y之间会出现差C，这就是关联矩阵：C=XT-Y。在此关联矩阵作用下，可以实现较好的迁移，并借助一个等式进行确定，即M=M0+CU。其中的U是Σ的T变迁导致的序列，而Petri网的状态方程，则表示为Mn+1=Mn+CU，其中Mn+1和Mn处于非常接近时，会停止运算。

3 工业机器人的柔性系统的故障诊断

通过上述的分析结合实际生产过程，不难发现，导致工业机器人发生故障，其表现形式涉及到了控制系统故障、执行系统故障等。此外，还包含了检测传感系统故障、气动系统故障等。

3.1 构建故障树

（1）减压阀、空气压缩机、管道出现的故障会导致气动系统出现故障。其中，空气压缩机故障的原因是进排气口堵塞、进口温度过高等造成的。管道系统故障是受到了管道破裂、管道堵塞的影响不能正常运作。其中导致出现减压阀故障的原因，与阀门破裂、闸阀未开均、螺钉螺母连接松动等存在直接关系。

图3 工业机器人Petri网模型

（2）在执行系统故障中，涵盖了腕部回转故障、手臂回转故障等，还包含了腰部回转故障、末端执行器故障等。其中手臂回转和腰部回转故障的主要表现就是发生电机、谐波减速器的损坏，同时连杆机构松动；造成腕部回转故障是因为锥齿轮、传动轴发生损坏、关节处螺栓发生松动等；末端执行器故障则主要是因为齿条齿轮没有准确啮合、驱动杆难以运作、抓取物超出承受范围导致的。

（3）在控制系统故障中，可以划分为硬件、软件两个方面的故障。其中，导致硬件系统发生故障的主要原因是因为示教模块、六轴运动控制模块发生故障，导致阻值偏大而导致的。而软件系统故障的发生，则主要是因为示教编程错误、参数设置错误、速度控制失效、位置控制失效造成的。

（4）速度检测、位置检测两部分故障是导致检测系统发生故障的主要原因。如果速度检测系统无法正常运行，会出现灵敏度较差、偏置电压不稳的情况；位置检测系统故障有电位器故障、旋转变压器故障等。

3.2 构建故障Petri 网模型

结合工业机器人故障树构建出对应的工业机器人故障的Petri网模型，如图3所示。

3.3 故障关联矩阵

根据上文分析出的C=XT-Y，得出关联矩阵C。如果初始故障表现为旋转变压器阻值偏大，也就是库所P4、含有托肯，可以得出初始标识向量为：M0=(0，0，0，1，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0)T，P4能够被触发，进而明确了初始标识向量U0=(0，0，0，1，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0)T。在此基础上，根据Petri网状态运用Matlab软件编写程序，可以实施后续计算，最终得出M1、M2、M3、M4、U1、U2、U3。

3.4 故障路径验证

结合上述计算结果，从M0到M4的过程，在P4、P23、P40等中都有托肯以及该库对应的故障。对于出现这一故障，工业机器人Petri网模型发生故障，则主要表现为P4、P23、P40、P46、P48。综上可知，通过故障树分析法和Petri网模型的综合运用，实验证明了故障传播路径与实际相符；同时，也说明了此种故障诊断技术可以应用到实际中。结语：本文通过对工业机器人柔性系统的故障诊断分析可知，此种故障诊断方法能够及时、准确的诊断、排查出工业系统故障问题。我们可以发挥关联矩阵的优势，快速找出问题；同时，借助Matlab软件的计算优势，运用对应的拟仿真形式，对比模拟结果，进而找出相应的故障问题。