斜轴式轴向柱塞泵装配序列规划和评价研究

2021-05-21陈永当宋辛辛顾金芋曹坤煜郑星

机械制造与自动化 2021年2期

陈永当，宋辛辛，顾金芋，曹坤煜，郑星

(1. 西安工程大学西安市现代智能纺织装备重点实验室，陕西西安 710600； 2. 西安交通大学，陕西西安 710049)

0 引言

斜轴式轴向柱塞泵结构紧凑，零件种类较多、结构复杂，由于装配方案和装配质量对斜轴式轴向柱塞泵的功能、性能有较大的影响，这对斜轴式轴向柱塞泵的装配规划提出了较高要求[1]。

装配序列规划作为数字化装配领域的重要研究课题之一，装配序列的合理性直接决定了装配工艺及过程的复杂程度，并影响产品的装配质量与装配成本[2]。传统的装配序列的规划方法有：拆卸法、割集法、几何推理法等[3-5]。在装配过程中，由于装配件的零件数量较多，易产生许多装配的可能性序列，即“组合爆炸”的问题。

由于求解得到的可行装配序列一般有多个，不同的装配序列对装配质量、成本、生产效率和可靠性的影响是不同的[6]，因此对装配序列进行评价、筛选是必要的。研究人员对装配序列的评价方法已经有了大量的研究，主要集中在装配时间、装配成本、操作简便性、并行度、稳定性等方面[7-8]。

为此，本文首先采用层次化割集法将斜轴式轴向柱塞泵装配体分解成若干子装配体和聚族，并求解装配序列。然后，对装配序列进行可行性分析，以获得可行装配序列，主要考虑了几何可行性、机械可行性和技术可行性等5个条件。最后，综合考虑装配的复杂性、时间、成本等因素，从4个方面对可行的装配序列进行了综合评价，得到最优的装配序列。

1 层次化割集法

1.1 层次化割集法算法

层次化割集法的流程图见图1，具体步骤为：1)根据装配体的装配关系信息提取子装配体和聚族，构造层次关系树及联接关系模型；2)根据层次关系树得出完全割集矩阵，去除伪割集[9]，并判断割集的可行性；3)根据可行割集及层次关系树求解出每一层的装配关系与或图，并输出可行的装配序列。

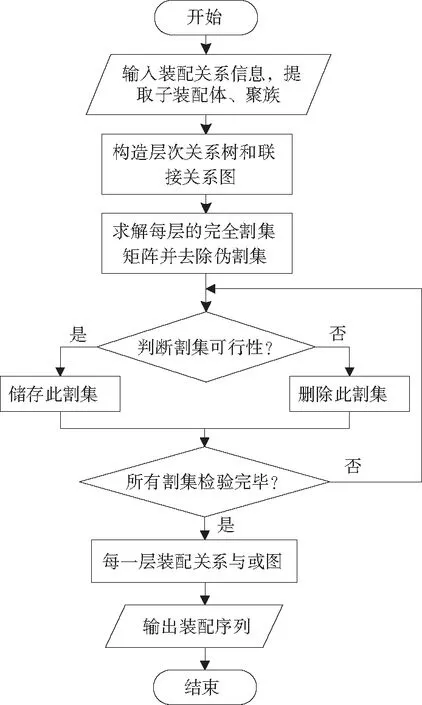
图1 层次化割集法算法流程图

1.2 层次关系树与联接关系模型

根据装配关系信息，提取装配体中的子装配体、聚族，并建立层次关系树。由图论知识可知，装配层次关系树中节点表示装配体或零件，树枝表示零件与装配体之间的层次关系[9]。图2为一装配体层次关系树示例。

图2 层次关系树

构造装配体零件之间的装配关联图G=(V，E)，其中V为节点，代表零件，E为节点的直接连接边，表示零件之间的连接关系。

1.3 完全割集矩阵与自由度矩阵

1)完全割集矩阵

完全割集矩阵是由联接关系图G=(V，E)的所有割集组成的矩阵，矩阵中的行表示对应的割集，列表示联接关系图中的边，其矩阵表达式为：

(1)

其中：aij取值为0或1，当边j在某割集中时，取值为1，否则，取值为0；i=1,2,…,2p-1-1，j=1,2,…,q，p为节点总数，q为连接边总数。

2)自由度矩阵

为判断稳定性和几何可行性，引入了局部运动自由度矩阵、内部分离运动自由度矩阵、内部运动自由度矩阵。规定零件具有±x、±y、±z6个方向的自由度，用1表示沿某方向具有局部运动分离自由度，0表示沿某方向无局部运动分离自由度。用PLM(Ei:aij|aik)表示零件aij和aik之间局部运动自由度矩阵，其表达式为：

(2)

其中：Ei表示装配割集中的任一条联接边；F±x、F±y、F±z分别表示沿±x、±y、±z方向的自由度。

内部分离运动自由度矩阵DFM(SA|Ck)表示子装配体SA分离成两部分时具有的运动自由度，其表达式为：

(3)

其中Ck表示联接关系图对应的一个割集。

内部运动自由度矩阵IFM(SA)表示子装配体SA内部零件之间相对运动关系的总和，其表达式为：

(4)

其中C表示联接关系图对应所有装配割集。

1.4 可行性判断方法

由于层次化割集法生成的割集只具有数学意义，为了剔除无意义的割集，需要对割集的可行性进行判断。割集的可行性判断主要包括装配序列的几何可行性、机械和技术可行性以及子装配体的稳定性和安全性。为了简化计算，尽早剔除不可行的割集，本文利用5个条件进行判断，其流程图如图3所示，具体包括：1)子超集规则；2)几何可行性；3)机械可行性；4)技术可行性；5)稳定性和安全性[10]。

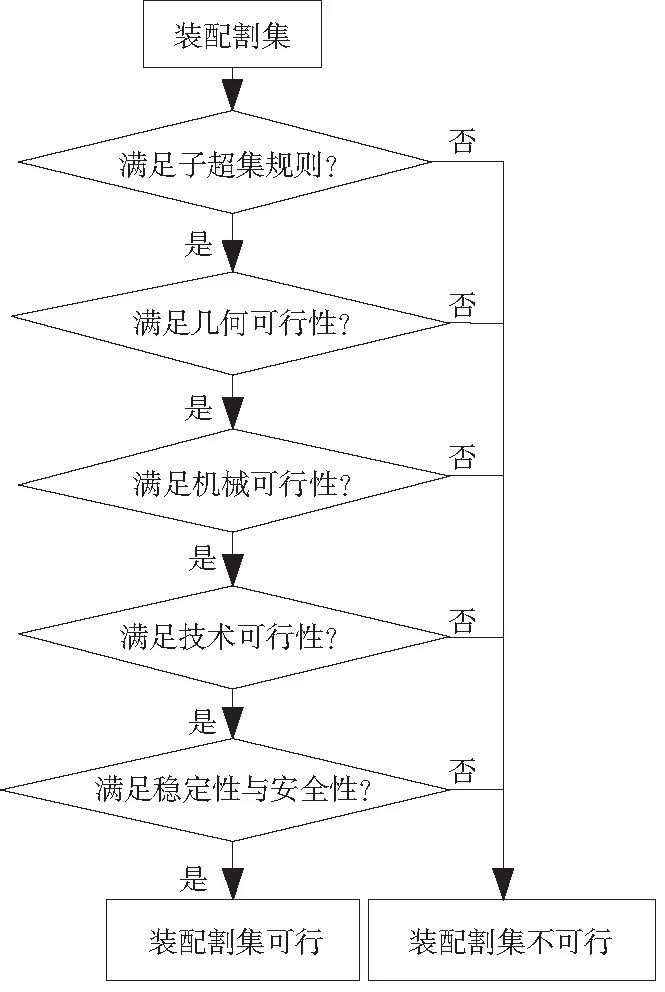
图3 割集可行性判断

2 斜轴式轴向柱塞泵装配序列的求解

2.1 斜轴式轴向柱塞泵装配信息模型

斜轴式轴向柱塞泵的三维模型如图4所示。

1—弹性垫圈；2—内六角螺钉；3—配流盘；4—密封环；5—柱塞；6—中心轴；7—十字螺钉；8—传动轴；9—推力调心滚子轴承；10—轴承挡圈；11—调整衬套；12—挡板；13—唇形密封圈；14—定位螺栓；15—壳体；16—孔用卡环；17—端盖；18—密封环；19—轴用卡簧；20—圆锥滚子轴承；21—压板；22—连杆；23—中心轴挡板；24—缸体；25—平行销；26—后端盖。图4 斜轴式轴向柱塞泵

2.2 建立层次关系树与联接关系模型

基于层次化割集法，本文将斜轴式轴向柱塞泵划分为2个装配体和4个聚族。为构建斜轴式轴向柱塞泵的装配体层次关系树，根据已确定的子装配体和聚族，将斜轴式轴向柱塞泵的模型分为5层的装配结构树，如图5所示。

图5 斜轴式轴向柱塞泵装配层次关系树

根据斜轴式轴向柱塞泵各零件之间的约束关系，构造联接关系模型(图6)以表示装配体的二维拓扑结构，其中：实线表示零件之间具有约束关系；虚线表示零件之间具有全局装配干涉关系。

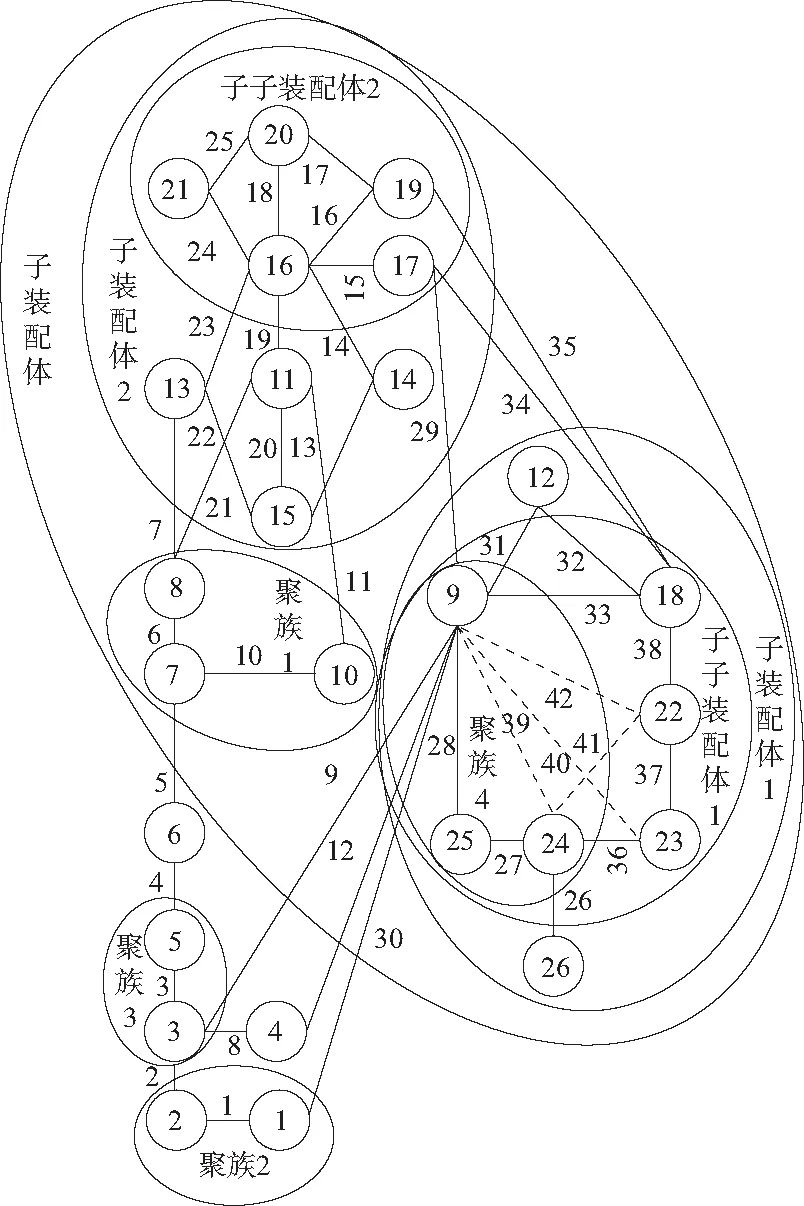
图6 斜轴式轴向柱塞泵联接关系模型

2.3 分层求解装配序列

利用层次化割集法和可行性判断条件对斜轴式轴向柱塞泵的装配序列进行逐层求解，求解的步骤为：首先，求解每一层零件之间的联接关系图；然后，根据层次割集法算法分别求出其去除伪割集后的完全割集矩阵；最后，对每一个割集进行可行性判断，从而求出与或图和可行的装配序列。根据斜轴式轴向柱塞泵装配层次关系树和联接关系模型，对斜轴式轴向柱塞泵装配序列进行求解，结果如表1所示。

3 斜轴式轴向柱塞泵装配序列评价

3.1 装配序列评价标准

通过层次化割集法生成装配序列的过程中虽然删除了大量不可行的装配序列，但仍存在很多可行的装配序列。为了筛选出最合适的装配序列，必须对装配序列进行综合评价。因此，本文综合考虑了多种因素的影响，主要从操作的并行性、重定向次数、聚合性准则和操作的复杂性4个方面建立评价模型[8]，见图7。

图7 评价模型

表1 斜轴式轴向柱塞泵装配序列求解结果表

3.2 装配序列评价结果

采用建立的评价模型，分别对5层可行的装配序列进行评价，得出最优的装配序列如表2所示。经评价标准筛选，装配序列中最大重定向次数和夹具数如表3所示。所得最优装配序列具有重定向次数少、操作并行性强、使用夹具少等优点，4个聚族可并行操作，装配操作简单。因此，通过采用本文建立的评价模型，筛选出的最优装配序列可有效提高装配生产效率，降低生产成本。