自重构仿生四足机器人运动学分析及仿真

陈刚，东辉

(福州大学 机械工程及自动化学院，福建 福州 350108)

0 引言

自重构模块化机器人是在可重构模块化机器人的基础上衍生出更加智能化、适应性更强的模块化机器人，每个模块都具有独自的控制系统、通讯系统和处理信息的能力，它可以在复杂环境中独自完成机器人的构型和工作姿态，相比传统机器人更具有独立性、灵活性和广泛的应用性，可应用到野外作业、井下搜救及管道清理等复杂环境中。多个相同单元模块可以组成环形机器人[1]、四足机器人等构型的仿生机器人。目前模块化机器人与其他机器人相结合构成仿生机器人是一个很热门的研究课题，如国外的SMORES[2]、国内的Trimobot等自重构模块化机器人[3]都与移动机器人相结合构建成多足仿生机器人[4]。

本文中自重构模块化机器人单元模块有三个自由度，在构成仿生四足机器人时，单元模块自由度有不同的功能，如有些自由度可以构成仿生四足机器人的腕关节、膝关节等。根据单元模块的机构理念，提出一种自重构仿生四足机器人。该仿生机器人是由多个相同的单元模块构成，在仿生四足机器人某个关节出现问题需要更换时，模块化便于更换，节约时间。运用D-H法转换对仿生四足机器人正逆运动学求解进行了分析，通过对仿生四足机器人进行运动仿真，验证了仿生四足机器人设计的合理性与理论推导的正确性。

1 单元模块与自重构仿生四足机器人特性描述

1.1 单元模块的特性描述

根据自重构模块化机器人模块之间的相互连接及关节自由度的分配，提出一种三自由度模块化设计。模块外观与内部结构如图1和图2所示，单元模块的尺寸为150 mm×110 mm×110 mm。主要由单元模块机体结构和连接结构构成。单元模块机体有三个自由度，分别为上摆动自由度、下摆动自由度与中间的旋转自由度。上、下摆角为±70°，中间的旋转角为360°，三个自由度相互独立。连接结构分为主动连接面和被动连接面，且安装在上、下摆杆的尺寸相同，主、被动连接面可以安装在任意摆杆上。一般情况下，下摆杆安装被动连接面，上摆杆安装主动连接面。连接方式为插销式连接。

图1 单元模块外观图

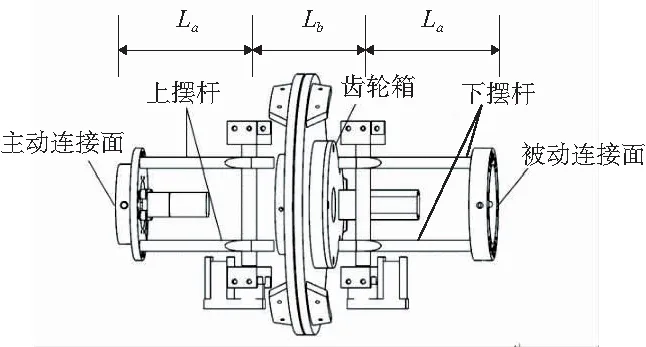
图2 单元模块内部结构图

1.2 自重构仿生四足机器人的特性描述

自重构仿生四足机器人是由10个单元模块构成，如图3所示，该仿生四足机器人每条机械腿由两个单元模块构成，机体由两个模块构成，其中机体单元模块6的上、下摆杆安装主动连接面，单元模块3的上、下摆杆安装被动连接面，便于仿生四足机器人机体的对称性，其他单元模块都是上摆杆安装主动连接面，下摆杆安装被动连接面。仿生四足机器人单元模块之间所有连接方式均为主、被动面连接。仿生四足机器人是以“腿III—腿I—腿IV—腿II”顺序进行运动的。

图3 仿生四足机器人结构图

机械腿IV由单元模块1和模块2所构成，每个单元有三个自由度，即共有六个自由度，如果每个自由度都运动，则产生多余的能量消耗与运动的冗余，且计算复杂。考虑这些因素，对自由度进行简化处理，假设单元模块1的下摆杆和中间自由度与模块2的中间自由度视作刚体。单元模块2的上摆杆自由度与四足机器人的机体连接，简化后的机械腿有三个自由度，其他机械腿的自由度简化与机械腿IV一样。每个机械腿足端装配一个半圆形橡胶垫，减少与地面的冲击力。

2 仿生四足机器人运动学分析

2.1 运动学建模

以机械腿IV为例，对自重构仿生四足机器人进行运动学分析。把机械腿各关节简化为连杆机构，在机器人机体与机械腿的各关节建立坐标系，如图4所示。机器人坐标系Oc-xcyczc建立在机体上，原点为机体质心点，yc正向为机体移动的方向，zc的反向为重力方向。坐标系O0-x0y0c0建立在机体与机械腿连接的关节处，原点Oc在机体中的坐标为(a,b,c)。坐标系O3-x3y3z3建立在机械腿足端与地面接触处。机械腿IV各关节参数如表1所示。

图4 机械腿IV的D-H坐标系

表1 关节参数

2.2 运动学正解

机体坐标系与机械腿IV的第1个关节坐标系矩阵变换为：

(1)

仿生四足机器人机体坐标系到机械腿IV与地面接触的坐标系矩阵变换为：

Ac3=Ac0A01A12A23=

(2)

所以可得仿生四足机器人足端末端位置坐标为：

(3)

式中：cij=cosθicosθj-sinθisinθj；sij=sinθicosθj+cosθjsinθi；Px、Py、Pz表示足端末端的坐标。

为了验证上面的正运动学运算是否正确，以机械腿IV为例，对各角度进行赋值：θ1=0°，θ2=-30°，θ3=-60°带入足端坐标Px、Py、Pz中进行验证可得：

(4)

与图4位置一致，说明求解正确。

2.3 运动学逆解

运动学逆解是根据机器人的末端位姿求出机器人各关节的角度。本节通过逆运动学求出机械腿IV关节角度θ1、θ2与θ3的值。

仿生四足机器人的机械腿IV位姿可表示为:

(5)

1)求θ1

根据式(2)：Ac3=Ac0A01A12A23

(6)

(7)

式中：f11(a)=nxc1+nys1；f21(a)=nz；f22(a)=oz；

f12(a)=oxc1+oyc1；f31(a)=nxs1-nyc1；f32(a)=oxs1-oyc1；

f23(a)=αz；f31(a)=nxs1-nyc1；f33(a)=αxs1-αyc1。

取第三行第四列，可解出θ1：

(8)

2)求θ2和θ3

(9)

式中：T=pys1-bs1+pxc1-ac1-l1；

f11(b)=nzs2+nxc1c2+nyc2s1；

f12(b)=ozs2+oxc1c2+oyc2s1；

f13(b)=αzs2+αxc1c2+αyc2s1；

f21(b)=nzc2-nxc1s2-nys1s2；

f22(b)=ozc2-oxc1s2-oys1s2；

f23(b)=αzc2-αxc1s2-αys2s1；

f31(b)=nxs1-nyc1；f32(b)=oxs1-oyc1；

f33(b)=αxs1-αyc1。

取第一行第四列与第二行第四列可得等式：

s2(pz-c)+c2T-l2=l3c3

(10)

c2(pz-c)-s2T=l3s3

(11)

式(10)与式(11)平方相加可解出θ2为：

(12)

将θ2带入式(11)中，可解出θ3为：

(13)

3 运动学仿真

将仿生四足机器人导入Adams环境中，对该机器人在一个周期中进行运动学仿真分析。图5为仿生四足机器人行走步态仿真截图，机器人分别迈腿III—腿I—腿IV—腿II且机体前移，完成一个周期行走步态，可看出仿生四足机器人行走稳定，设计合理。

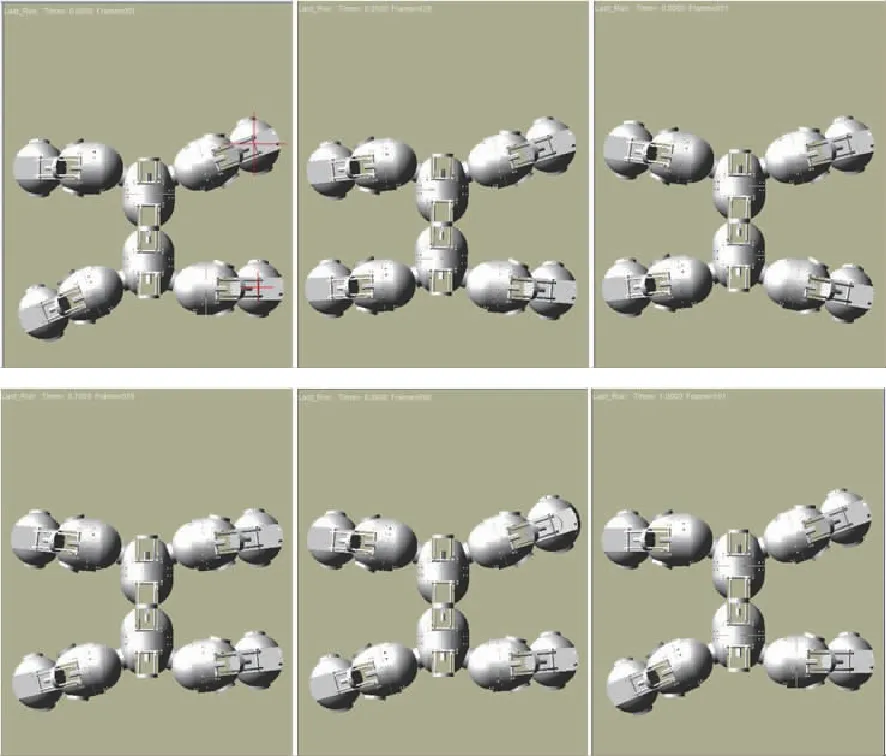
图5 仿生四足机器人的行走步态仿真截图

图6为机械腿IV足端在yOz平面下的运动轨迹，足端运动轨迹类似于抛物线，y轴为四足机器人的前进方向，z轴为垂直地面方向。机械腿的运动曲线连续。图7中质心在x轴左右方向上的运动位移约为0，在y轴前进方向上连续运动，表明自重构模块化四足机器人在y轴方向做直线运动。

图6 机械腿IV足端的运动轨迹

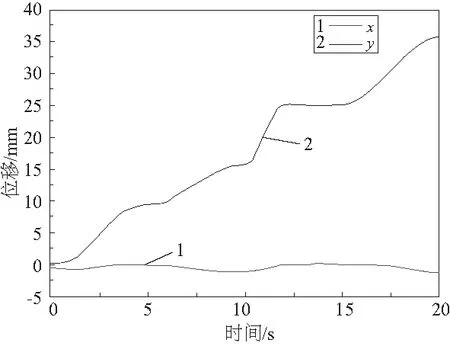
图7 机体质心前进位移

从图8、图9可以看出自重构仿生四足机器人足端速度和角速度曲线连续，没有发生突变，在行走过程中较平稳，在10～15 s时机械腿IV足端行走一个步伐，在这段时间足端的速度和角速度有一个上升和下降的幅度。

图8 机械腿IV足端速度

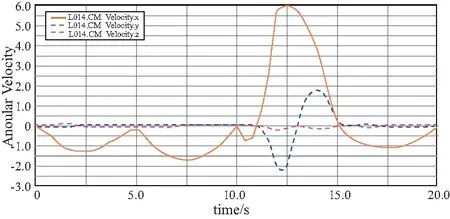
图9 机械腿IV足端角速度

4 结语

本文通过对自重构模块化机器人单元模块进行分析，提出一种新型自重构仿生四足机器人。对仿生四足机器人进行详细的正运动学和逆运动学分析，并在Adams中进行仿真，得到了机器人在行走过程中一些轨迹与速度曲线。通过对曲线的分析，验证了自重构仿生四足机器人平稳行走的合理性与理论推导的正确性。