一种不考虑评价指标赋值的采矿方法优选模型*
2021-05-21李斌
李 斌
(西南科技大学 环境与资源学院,四川 绵阳 621010)
0 引言
采矿方法与井下生产和矿山经济效益密切相关,是地下矿山开采设计的基础和关键。因此,采矿方法的优选一直是采矿工程领域的基础研究课题。传统的工程类比法对采矿方法的确定具有一定的指导意义,但其过于依赖主观经验,科学合理性有所欠缺。鉴于此,随着交叉学科的发展,系统科学理论中的决策方法被引入采矿方法的优选研究中[1]。
采矿方法的优劣一般可根据生产能力、矿石回收率、采矿安全性等多项技术经济指标进行综合评价。因此,采矿方法优选在系统科学理论中是一个典型的多属性决策问题[2-3]。基于以上认识,已有许多学者采用多种形式的决策模型开展了采矿方法优选研究,如:王新民等[4]采用模糊综合决策的方法确定了最优采矿方案;刘志祥等[5]采用逼近理想点法进行了采矿方法优劣排序;叶义成等[6]采用区间数排序方法对采矿方案进行了优选。这些决策方法在应用时需要给出决策矩阵,即决策时各采矿方案必须要有具体的评价指标属性值。但是,针对待采矿体设计采矿方案时,难以赋予各评价指标具体的属性值,通常只能依靠工程类比选取估计值,或根据实践经验确定各采矿方案在某一指标下的优劣。目前,鲜有成果从这一认识角度出发开展采矿方案的优选研究工作。
秉着科学的简单性原则,本文将3标度应用于特征向量法来确定指标权重,结合线性分配法构造一种简单的不考虑具体评价指标赋值的决策模型,并将其应用于矿山的采矿方法优选。
1 采矿方法优选模型
假设采矿方法优选的多属性决策问题中有n个评价指标:G1、G2、…、Gn;m个备选采矿方案:A1、A2、…、Am。
1.1 采用特征向量法确定指标权重
1.1.1 构造判断矩阵
特征向量(EV)法[7]常用的1-9标度法由于赋值区间跨度大,一般存在难以准确定量判断两个指标间的相对重要程度的问题,如重要和明显重要有时难以严格区分。3标度法赋值区间跨度相对较小,仅需判断指标Gi是否比指标Gj重要,而不用判断其重要程度。因此,采用3标度可更加简单快速地构造判断矩阵。3标度法确定比较判断矩阵C=(cij)n×n中元素cij的公式为
(1)
令
(2)
进一步构造出新矩阵B=(bij)n×n。其中,bij的取值为
(3)
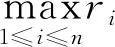
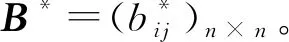
aij=lgbij,
(4)
(5)
(6)
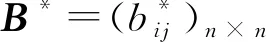
1.1.2 求解特征向量
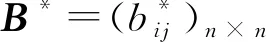
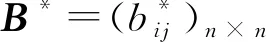
(7)
b.计算mi的n次方根,得
(8)
c.对特征向量W=(w1,w2,…,wn)T按下式进行归一化处理:
(9)
(10)
1.2 线性分配法构建优选模型
先做基本假设:每个采矿方案必须且只能排在一个位置,而排序中的每一个位置必须且只能排一个采矿方案。基于该假设,线性分配法[10]构建采矿方案优选模型的基本思路为:决策者采用德尔菲法或根据工程经验判断在每个评价指标下,m个备选采矿方案的优劣排序(n个评价指标即有n个排序结果),再结合各评价指标权重,构造排序优势矩阵,求解最优排序矩阵,进而确定各采矿方案的最终优劣排序。具体决策过程叙述如下。
a.构造采矿方案排序优势矩阵D=(dij)m×m。其中,元素dij为采矿方案Ai排在第j位的各评价指标的权重之和。
b.求解采矿方案排序矩阵P=(pij)m×m。其中,pij=1表示采矿方案Ai最终排在第j位,其余pik=0(k=1,2,…,m;k≠j)。则该矩阵为以下整数规划模型极大化的指派问题的最优解:
(11)
令
(12)
则模型(10)可等价转化为以矩阵E=(eij)m×m为效率矩阵的标准形式指标问题,即
(13)
式(13)可采用匈牙利法[11]进行求解,其结果即为采矿方案排序矩阵P=(pij)m×m。
c.求解采矿方案的最终排序向量,A*=[A1A2…Am]P,最终得到各采矿方案的优劣排序结果。
2 工程应用
湖北省中部某地下铁矿山由于采用无底柱分段崩落法进行采矿生产,已造成部分地表塌陷,且地表移动带逐渐靠近选矿车间。目前,该矿山开采至-430 m水平,根据岩层移动角(约62°)和安全距离临界点将正在开采的Ⅲ#矿体划分为两部分(见图1)。西侧部分(即选矿车间压覆矿体)如果继续采用崩落法开采,则必然会威胁到选矿车间的安全,而东侧部分则可继续采用崩落法开采。因此,有必要改用充填法开采该压覆矿体。
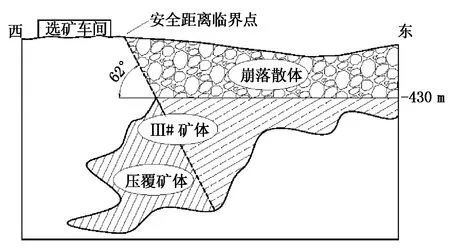
图1 开采现状示意图
根据压覆矿体的开采技术条件,经过初选,确定了3种备选充填采矿方案:上向进路充填法A1、下向进路充填法A2、分段留矿嗣后充填法A3。根据矿山的实际开采要求,选定了6个指标:块矿生产能力G1、采矿安全性G2、矿石损失率G3、矿石贫化率G4、采切比G5和采充成本G6。
2.1 确定指标权重
根据矿山单位意见,采矿方案需考虑以下原则:①保证采矿作业不给选矿车间带来威胁;②以较低成本最大程度地回采矿石;③较小的工程量和较高的采矿效率;④尽可能降低矿石的贫化。因此,确定上述6个指标的相对重要性排序为G2>G6>G3>G5>G1>G4。
根据以上6个指标的相对重要性排序结果,按照式(1)-式(9)计算得到指标权重矩阵W*=[0.038 0.468 0.139 0.022 0.072 0.261],并代入式(10)计算得到最大特征根λmax=6。
2.2 一致性检验
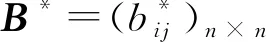
(14)
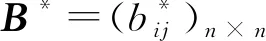
由前所述,最大特征根λmax=6,评价指标个数n=6,代入式(14)可得RC=0,通过一致性检验,表明EV法确定的6个指标的权重科学合理,也进一步验证了应用3标度的特征向量法构造的判断矩阵满足一致性要求。
2.3 各指标下的采矿方案排序
在不考虑各指标具体属性值的条件下,根据矿山工作人员和相关科研单位对各备选采矿方案在每个评价指标下的优劣排序,采用德尔菲法得到3种备选采矿方案分别在6个评价指标下的综合优劣排序结果(见表1)。
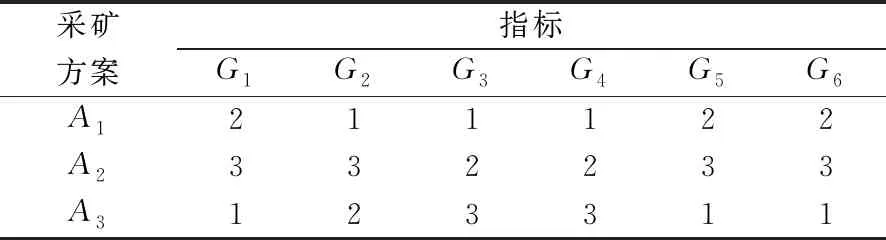
表1 各指标下采矿方案的优劣排序
表1中的数字表示其对应行的采矿方案在其对应列的指标下的排位。由表1可知:方案A1在指标G2、G3、G4下均排第1位,在指标G1、G5、G6下均排第2位;方案A2在指标G3、G4下均排第2位,在指标G1、G2、G5、G6下均排第3位;方案A3在指标G1、G5、G6下均排第1位,在指标G2下排第2位,在指标G3、G4下均排第3位。
2.4 确定采矿方案的最终排序
根据表1中3种备选采矿方案分别在6个评价指标下的优劣排序结果,结合2.1节中的各评价指标权重,确定采矿方案排序优势矩阵D=(dij)3×3为
(15)
式中,最大元素为d23=0.839。则排序优势矩阵D=(dij)3×3按式(12)可转化为
(16)
则采矿方案排序矩阵P=(pij)3×3为以下标准形式指派问题的最优解:
(17)
应用匈牙利法求解式(17),得采矿方案排序矩阵P=(pij)3×3为
(18)
从而得到采矿方案的最终排序向量A*=[A1A3A2],即应优先选择上向进路充填法(方案A1)开采该压覆矿体。
2.5 有效性分析
从系统科学理论角度而言,针对多属性决策问题,选择不同的决策思路及决策方法,得出的决策方案可能存在差异。本文采矿方法优选模型的思路为:若方案几个重要的指标均排在前面,则总体上看该方案很有可能也排在前面。
由式(15)可知,方案A1、A2、A3排第1位的各指标权重之和分别为0.629、0.371、0,可认为可能排第1位的方案优先顺序为A1>A2>A3。同理,可能排第2位的方案优先顺序为A3>A1>A2,可能排第3位的方案优先顺序为A2>A3>A1。因此,最有可能的结果为方案A1排在第1位,方案A3排在第2位,方案A2排在第3位。本文这种不考虑评价指标赋值的采矿方法优选模型正是基于以上决策思路提出的,2.4节中决策出的结果也与该思路的结果具有较好的一致性。
3 结论
a.采用特征向量法确定指标权重时,为减少主观性,引入3标度法代替1-9标度法来快速构造比较判断矩阵,经过简单转换后得到的判断矩阵满足一致性检验要求。
b.用特征向量法和线性分配法建立了不考虑评价指标赋值的采矿方法优选模型。该模型具有过程简单、计算量小的特点,适用于缺少指标赋值的多属性决策问题。
c.将本文构建的模型应用于某地下矿山选矿车间压覆矿体的充填开采方案优选中,决策得到的最优采矿方法为上向进路充填法。
