隐藏在中考题中的“摸球试验”

文 秦建敏

这几年，围绕概率的问题逐渐由考查概念和计算转为考查阅读、理解以及实际运用，这部分试题往往材料新颖、图文并茂。但是简单的随机事件的概率问题本质上都可以转化为等可能条件下的摸球试验问题。下面我们通过几道中考题加以阐述，以便大家更好地认识中考中的概率问题。

例1（2020·湖南湘潭）生死守护，致敬英雄。湘潭28名医护人员所在的湖南对口支援湖北黄冈医疗队红安分队，精心救治每一位患者，出色地完成了医疗救治任务。为致敬英雄，某校音乐兴趣小组根据网络盛传的“红旗小姐姐”跳的儋州调声组建了舞蹈队。现需要选取两名学生作为舞蹈队的领舞，甲、乙两班各推荐了1名男生和1名女生。（温馨提示：用男1、女1，男2、女2分别表示甲、乙两班的4名学生。）

（1）请用列举的方法写出所有可能出现的结果；

（2）若选取的两人来自不同的班级，且按甲、乙两班先后顺序选取，请用列表或画树状图的方法求出恰好选中1男1女的概率。

【分析】本题考查列表法和画树状图法，同时，按照题目中“写出所有可能出现的结果”的要求，在使用列举法时，要注意按一定的顺序列举，做到不重不漏。

（1）直接列举出所有可能出现的结果即可；

（2）画出树状图，找出符合题意的可能结果，再利用概率公式求出概率。

解：（1）可能出现的结果有：男1女1、男1男2、男1女2、男2女1、男2女2、女1女2。

（2）画树状图如下：

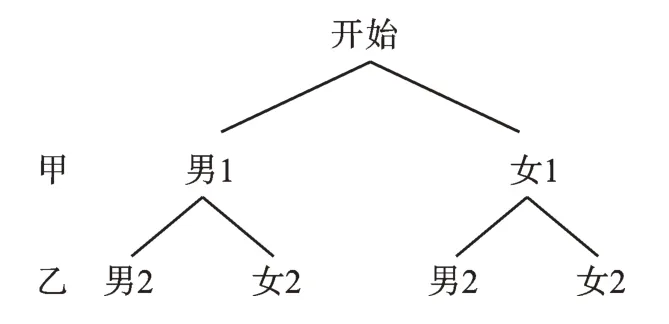
共有4种等可能的结果，其中恰好选中1男1女的结果有2种，所以恰好选中1男1女的概率为。

【点评】本题的第（2）小题，考查的是选中的学生为1男1女的概率。我们不妨把男生看作红球，把女生看作白球，甲班的男生、女生分别为红1、白1，乙班的男生、女生分别为红2、白2。那么此题就转化为从红1、白1和红2、白2中分别取1个球，求这两个球的颜色不相同的概率。这样，问题就顺利地从到班级选学生转化为摸球试验，回归熟悉的问题，思考起来简单明了。

例2（2020·辽宁营口）随着“新冠肺炎”疫情防控形势日渐好转，各地开始复工复学。某校复学后成立“防疫志愿者服务队”，设立4个“服务监督岗”：①洗手监督岗，②戴口罩监督岗，③就餐监督岗，④操场活动监督岗。李老师和王老师报名参加了志愿者服务工作，学校将报名的志愿者随机分配到4个监督岗。

（1）李老师被分配到“洗手监督岗”的概率为________；

（2）用列表法或画树状图法，求李老师和王老师被分配到同一个监督岗的概率。

【分析】（1）一共有4个监督岗，李老师被分配到每个监督岗的可能性相等，所以李老师被分配到“洗手监督岗”的概率为。

（2）在分配监督岗时，李老师有4种等可能的岗位分配，针对李老师的每一项岗位分配，王老师又有4种等可能的岗位分配，由此得出李老师和王老师所有的岗位分配种数。其中李老师和王老师被分配到同一个监督岗的情况有4种，进而求得相应概率。

解：（1）

（2）（方法一）画树状图，如图所示：

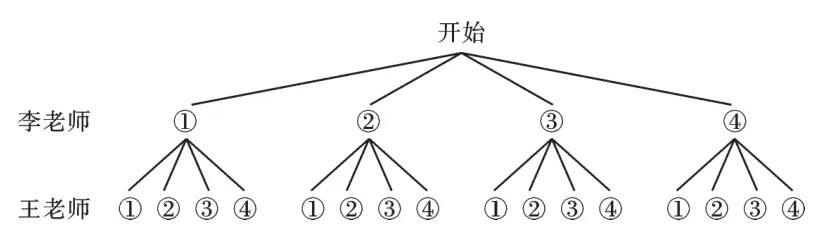
由树状图可以看出，随机将李老师和王老师分配到4个监督岗，可能出现的结果共有16种，并且它们出现的可能性相等，其中，两位老师被分配到同一个监督岗的情况有4种，即①①，②②，③③，④④，

∴P（两位老师被分配到同一个监督岗）

（方法二）根据题意，列表如下：

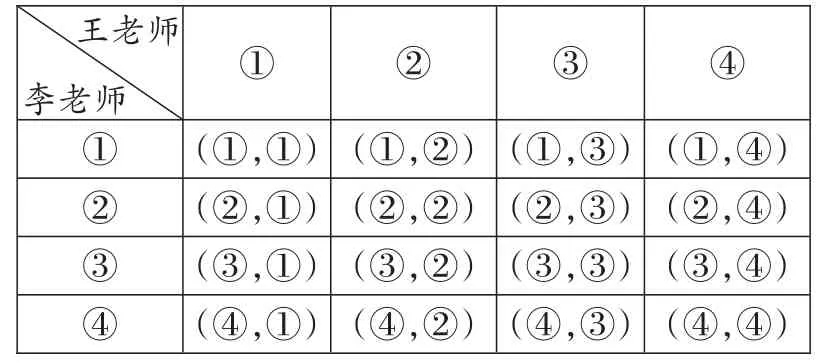
①②③④①（①，①）（②，①）（③，①）（④，①）②（①，②）（②，②）（③，②）（④，②）③（①，③）（②，③）（③，③）（④，③）④（①，④）（②，④）（③，④）（④，④）王老师李老师

由表格可以看出，随机将李老师和王老师分配到4个监督岗，可能出现的结果共有16种，并且它们出现的可能性相等，其中，两位老师被分配到同一个监督岗的情况有4种，即（①，①），（②，②），（③，③），（④，④），

∴P（两位老师被分配到同一个监督岗）。

【点评】这是一道以防疫监督岗人员调配为背景的实际问题，我们依然可以将它转化为摸球试验。“一只不透明的袋中装有标号分别为①、②、③、④的小球，这4个球除标号外完全相同，从中随机抽取一个小球，记下标号，放回后再从中随机抽取一个，求两次抽出小球标号相同的概率。”对大家来说，这个摸球试验是一个可以轻松应对的问题。

同学们，通过对这几个问题的分析，我们会发现，在数学的学习过程中，模型思想、转化思想是多么重要。数学是需要积累解题经验的，但是如果能在解决一类问题后，认真观察、思考、归纳其中的规律，对我们提高数学水平会有很大的帮助。