峰回路转看变换
——平移、折叠、旋转和构造
2021-05-21特级教师
文 赵 军(特级教师)
专题复习:图形的变化 图形与坐标
领 衔 人:赵 军(特级教师)
组稿团队:江苏省太仓市实验中学(太仓市赵军名师工作室)
解答数学问题,有几大必备策略:一类是图形的变换,包括平移、折叠(对称)和旋转;另一类是构造图形。通过这些方法,我们可以将问题进行转化,以达到化难为易的目的。
一、平移法
例1在如图1所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB
与CD相交于点E,则∠AED的正切值是____。

图1
【思路分析】所求的∠AED不在某一直角三角形中,如何求其正切值?策略1:自力更生,“就地”构造直角三角形;策略2:通过图形的变换,将此角进行转化。策略1:结合已知条件,求tan∠AED虽然可以转化为求tan∠CEB,然后在△CBE中作高,构造直角三角形求解,但点E不在格点上,所以求所构造的直角三角形的边比较麻烦;策略2:试着通过平移线段将∠AED转移到某一直角三角形中求解即可。
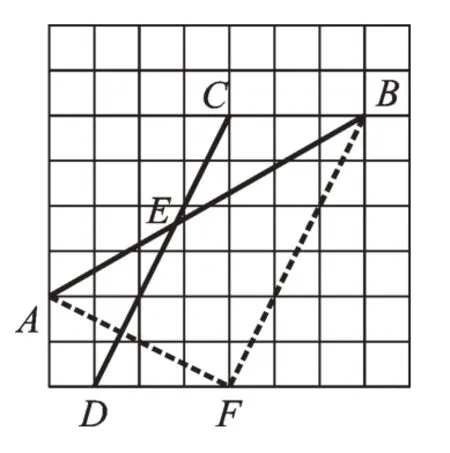
图2
如图2,将线段CD向右平移3格,使线段CD平移至BF,连接AF,在Rt△ABF中,所以∠AED的正切值为。
【归纳反思】当求值遇到困难时,应首先想到转化。所谓“山重水复疑无路,平移变换又一村”,借助平行,我们可以将所求的角进行转化,达到化难为易的目的。
二、折叠(对称)法
例2如图3,在平面直角坐标系中,点A(3,,P为x轴上一动点,则OP+AP的最小值为________。

图3
【思路分析】点A(3,的坐标隐藏了OA与x轴正方向的夹角为30°,如果能发现这个30°角,就为转化创造了条件。
如图4,连接OA,过点P作PB⊥OA,垂足为B,则在Rt△OBP中所以AP=PB+PA,问题即转化为求PA+PB的最小值。此时可作点A关于x轴的对称点A′,连接AA′,交x轴于点D,再将PA转化为PA′,最终将问题转化为点A′到OA的距离最短问题。
如图4,求A′C的长有三种思路:一是在连接OA′的基础上,运用等积法(两次计算△OAA′的面积)求解;二是证得△AA′C≌△AOD得到答案;三是运用锐角三角函数,分别在Rt△OAD和Rt△A′AC中,以sin∠OAD=sin∠A′AC解决问题。

图4
【归纳反思】通过对称变换,将求“和最小”的问题进行转化,由某直线同侧的“和最小”转化为该直线异侧的“和最小”。其思路概括为:“和最小,对称找”,从而将问题转化为点到直线的距离问题。
三、旋转法
例3如图5,在平面直角坐标系中,点A(12,0),点B(0,4),点P是直线y=-x-1上一点,且∠ABP=45°,则点P的坐标为 。

图5
【思路分析】点P可视作直线BP和直线y=-x-1的交点,所以求出直线BP的表达式是解题的关键。而直线BP过点B(0,4),因此,只需在该直线上再找一点或者求得该直线的k值即可。剩下的问题就是如何利用好条件∠ABP=45°,这时候我们可以考虑旋转线段。
如图6,将线段AB绕点B逆时针旋转90°至CB,过点C作CD⊥y轴,则容易得到△ABO≌△BCD、∠BAC=45°,所以可以得到C(4,16)、BP∥CA,在求出直线CA的表达式y=-2x+24后,根据“两直线平行,k值相等”,从而得到直线BP的表达式为y=-2x+4,最后列方程组解得点P的坐标为(5,-6)。
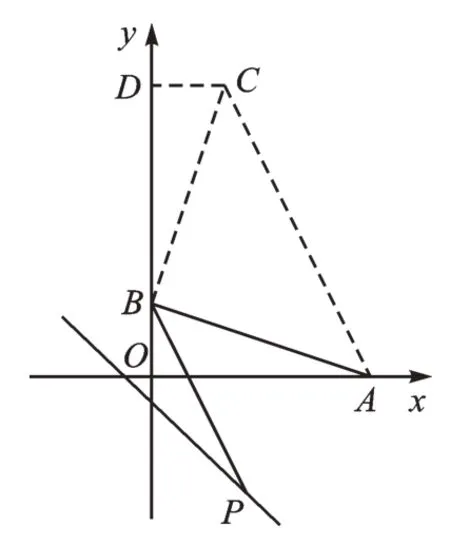
图6

图7
【归纳反思】将线段AB绕点B逆时针旋转90°的目的是构造等腰直角三角形,出现新的45°角,为直线的平行创造条件。当然,我们也可以将线段AB绕点B顺时针旋转90°(如图7),则CA与BP的交点E就是CA的中点。在求得点E坐标的基础上,求出直线BE的表达式,最后列方程组求得交点P的坐标。因此,旋转线段的直接效果是出现等腰直角三角形,若题目中有与之相关联的条件,可以尝试运用此法。
四、构造法
例4如图8,四边形ABCD是边长为4的正方形,⊙B的半径为2,点P是⊙B上一动点,则的最小值为________,PD-的最大值为________。

图8
【思路分析】如何找出一条线段代替是解题的关键。仔细读题,我们会发现:⊙B的半径为2,与正方形的边长4的比值是这与我们要找的线段长与PC之比相等,因此,考虑构造一组相似三角形,通过比值不变找出这条线段。
如图9,连接BP,取BE的中点F,连接PF、DF,由∠FBP=∠PBC,得△BFP∽△BPC,所以。问题即转化为求PD+FP的最小值。很显然,当D、P、F共线时,有最小值,最小值为DF的长。可在Rt△CDF中求得DF=5。同样的思路,FP,如图10,有PD-FP≤DF,所以当D、F、P三点共线(F在线段PD上)时,有最大值5。
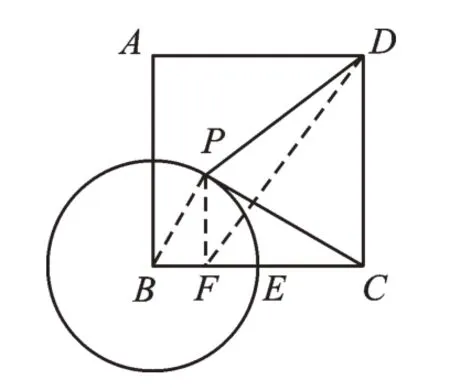
图9
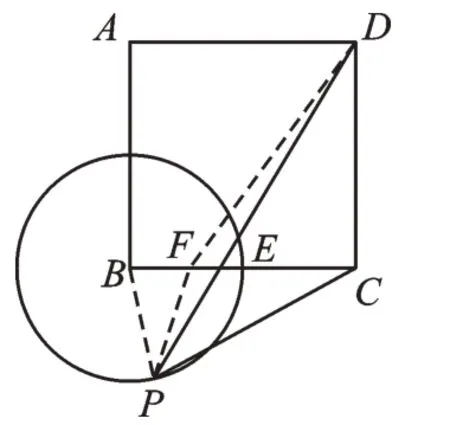
图10
【归纳反思】构造不是凭空捏造,它是有“根”的。本题的根在系数也是解题的“题眼”所在。因此,通过构造,我们化解了达到了转化的目的。
图形的变换是一种技巧。通过平移、折叠、旋转及构造,我们能有效地将问题化难为易,化陌生为熟悉。什么时候采用哪种变换,要据题目的条件而定,不能一概而论。一般而言,其运用技巧可以归纳为:角度摸不着,平移来帮忙;要求“和最小”,对称少不了;出现四十五,旋转估一估;系数是个比,构造试一试。
