图形变换题的设计思路及应对策略

文 夏济军

图形的变换主要以图形为载体，通过对图形的平移、翻折、旋转等方式，将图形的位置改变，并以此考查同学们分析问题和解决问题的能力。现结合2020年中考试题，从命题者的角度谈谈此类题目的设计思路及应对策略，希望对大家的学习有所帮助。

一、设计对称

例1（2020·江苏盐城）如图1，已知点A（5，2），B（5，4），C（8，1），直线l⊥x轴，垂足为点M（m，0），其中若△A′B′C′与△ABC关于直线l对称，且△A′B′C′有两个顶点在函数的图像上，则k的值为________。

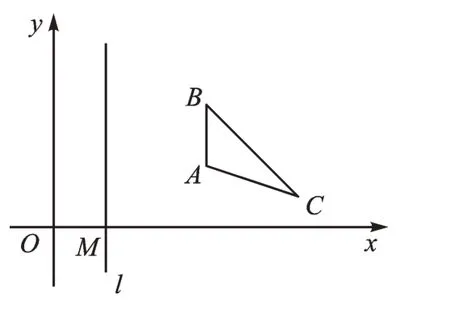
图1

【命题思路】（1）本题考查坐标的对称变换，由m的取值范围m＜，得△A′B′C′的3个顶点落在第二象限；（2）△A′B′C′有两个顶点落在反比例函数y=的图像上，考查了同学们分类讨论的意识。

【应对策略】第一步：因为△A′B′C′与△ABC关于直线x=m对称，所以纵坐标不变，横坐标之和的一半等于m，不妨设A′（x′，2），则=m，所以x′=2m-5，所以A′（2m-5，2）、B′（2m-5，4）。同理可求出C′（2m-8，1）。

第二步：分类讨论。当函数图像经过A′、C′两点时，k=xy=2（2m-5）=1（2m-8）；当函数图像经过B′、C′时，k=xy=4（2m-5）=1（2m-8）；当函数图像经过B′、A′时，这种情况不存在。分别解得m=1或2，所以k=-6或-4。

二、设计平移

例2（2020·河南）如图2，在△ABC中，∠ACB=90°，边BC在x轴上，顶点A、B的坐标分别为（-2，6）和（7，0）。将正方形OCDE沿x轴向右平移，当点E落在AB边上时，点D的坐标为（ ）。

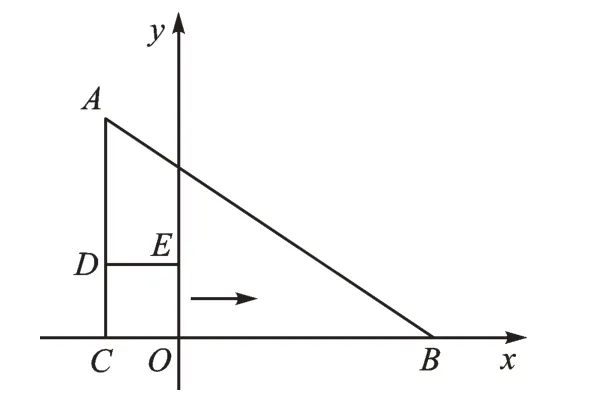
图2

【命题思路】通过平移变换、坐标与线段长度之间的转化，着重考查了同学们动手操作的能力和对正方形的性质、基本的相似图形以及锐角三角函数的运用能力，同时还考查了一次函数方面的有关知识。

【应对策略】首先将点的坐标转化为线段长，由点A（-2，6）可知OC=2，即正方形OCDE的边长为2，所以正方形OCDE沿x轴向右平移不改变点D的纵坐标2。如图3，先画出平移后点E落在AB上的示意图，思路1：抓住相似三角形的基本图形（正A型），由△BO′E∽△BCA可求得O′B=3，从而推算出点D的坐标为（2，2）；思路2：分别在Rt△ABC和Rt△EBO′中表示出tan∠ABC=tan∠EBO′得解；思路3：在求得直线AB函数表达式的基础上，令纵坐标等于2，求得点E的横坐标，由正方形边长为2，可以推算出点D的坐标。

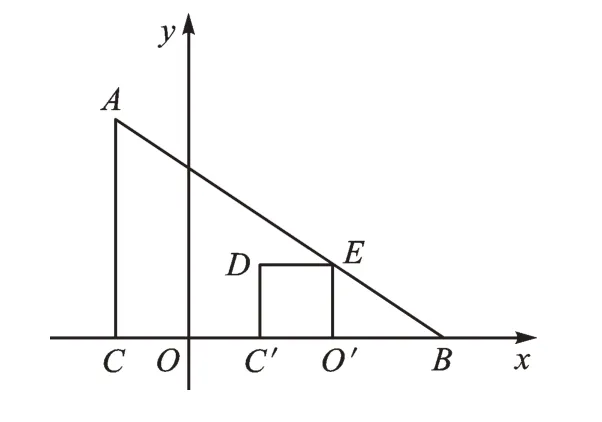
图3

三、设计旋转

例3（2020·江苏苏州）如图4，在△ABC中，∠BAC=108°，将△ABC绕点A按逆时针方向旋转得到△AB′C′。若点B′恰好落在BC边上，且AB′=CB′，则∠C′的度数为（ ）。

A.18° B.20° C.24° D.28°

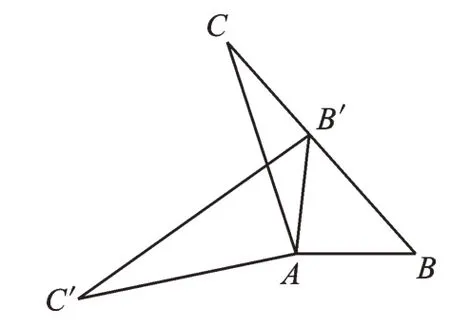
图4

【命题思路】利用三角形旋转的不变性（三角形形状、大小不改变，对应点到旋转中心的距离不变），如∠C′=∠C、AB=AB′，构造等腰三角形，考查了同学们对旋转变换的理解和运用方程解决问题的意识。

【应对策略】“设小表大”，列方程求解。所谓“设小表大”，就是设较小角的度数为x，并用含x的代数式表示出与之相关的较大角，然后从中找出相等关系并列出方程，最终解决问题。设∠C′的度数为x，则∠C=x，因为AB′=CB′，所以∠B′AC=x。接着利用△AB′C的外角表示出∠AB′B=2x，由旋转得AB=AB′，所以∠B=∠AB′B=2x。在△ABC中，据三角形的内角和等于180度可列方程x+2x+108=180，所以x=24，即∠C′的度数为24°。

图形的变换历来是中考考查的重要内容，我们只要抓住图形变化过程中变化的特征和规律，找准变化前与变化后始终保持不变的量，就能以不变应万变，解决多种问题。