面向立方星的相对位姿测量视觉传感器设计

2021-05-21杜荣华张兴星张翔汪玲

中国空间科学技术 2021年2期

杜荣华,张兴星,张翔,*,汪玲

1. 南京理工大学机械工程学院，南京 210094 2. 南京航空航天大学电子信息工程学院，南京 210016

航天技术发展中的重要内容之一是在轨服务技术。随着近些年国内外太空探索的进程加快，在轨服务技术亟待发展。在轨服务定义为服务航天器携带各种设备装置与目标航天器发生相互作用的过程。航天器由于故障、失效或者燃料耗尽而不能继续正常工作，在轨服务技术可用于故障航天器维修、回收，对于延长卫星服务寿命、减少太空环境碎片[1-2]，增强在轨卫星管理能力十分重要。在轨服务技术涉及与目标航天器的交会对接技术、绕飞检测技术和捕获技术等，而实现这些技术的核心是视觉导航技术[3-4]，其中服务星与目标星之间的相对位姿测量是进行视觉导航的基础。

国外已经开展了若干视觉导航在轨演示验证项目。如美国的轨道快车[5]计划，日本的ETS-VII[6]等。这两个项目中的追踪星均安装了可见光相机,目标星安装了发光标志器或角反射镜作为合作目标特征点。国内在航天器近距离的相对位姿测量技术研究中,也多采用合作标志器[7-8]。以上项目中的追踪星体积和质量一般较大，造价高，且需要配备复杂的仪器设备。

微纳卫星由于质量小、造价低和研制周期短的优势，近年来在国际上成为研究热点，其中具有代表性的是立方星技术。2018年美国和欧洲知名航天技术研究机构相继以立方星为平台，开展对微纳卫星视觉导航技术的在轨验证[9-10]，而中国尚未在该项技术上有足够的积累。瞄准立方星在未来在轨服务中的应用，本文解决立方星视觉导航技术中追踪星与目标星之间的相对位姿测量问题，设计一种立方星视觉传感器，并提出有效的位姿测量算法。

立方星视觉传感器的研制主要受到立方星的体积、质量和功耗的限制。瑞士洛桑联邦理工学院的Camille等[9]提出了一种适用于立方星平台的交会对接视觉测量方案。通过在追踪立方星上安装单目摄像机和在目标星上安装发光二极管来确保系统在整个接近过程中的可观测性。Tyvak纳米卫星系统公司[10-11]提出的立方星接近操作演示任务中，采用了两个可见光与两个红外相机，针对不同距离和光照的条件，采用不同视场的相机来实现两个3U立方星的在轨编队飞行与接近操作验证。帕多瓦大学的Sansone等[12]开发了一种与微纳卫星平台相兼容的红外相对导航传感器，用于微纳卫星的近距离的相对导航，该系统精度一般且适用范围有限。国内关于立方星的视觉导航技术研究尚处于起步阶段，尚没有大力开展以立方星为平台的视觉导航技术研究，不涉及在轨演示验证。

在完成若干立方星研制任务基础上，本文提出一种适用于立方星平台的相对位姿测量视觉传感器设计。首先，针对单目测量深度信息缺失的问题，在视觉传感器组成上提出一种多层立体靶标设计，并选择一种适合立方星平台的微型相机对设计的立体靶标进行成像。为应对空间复杂的光照环境，选取波长为850nm的LED灯作为立体靶标的光源，通过在微型相机镜头处安装850nm的红外窄带滤镜来提高立体靶标成像质量。针对视觉导航对相对位姿测量的高精度要求，提出一种IDS的位姿估计算法。最后搭建模拟真实空间光照和运动环境的六自由度实验平台对该视觉传感器进行性能测试，并通过不同相对位姿估计算法的对比分析校验提出的相对位姿估计算法的有效性。

1 视觉传感器设计

视觉传感器包括多层立体靶标、微型相机和数据处理模块等。本节将给出多层立体靶标设计、相机选型和有无红外窄带滤镜的图像获取性能测试。

1.1 多层立体靶标

现有的用于航天器视觉导航的合作靶标可分为平面靶标和立体靶标。根据靶标是否有源，又可分为有源靶标和无源靶标。无源靶标在图像处理的过程中，可能会由于图案特征信息不明显，使得靶标图案和背景的分离难度较大，应用具有较大的局限性，而平面靶标的缺陷是无法提供包含空间几何约束的信息。基于上述考虑，我们设计了一种具有多层结构的立体靶标用于视觉传感器获取相对位姿信息。图1给出了多层立体靶标的侧视图和靶标图案尺寸。

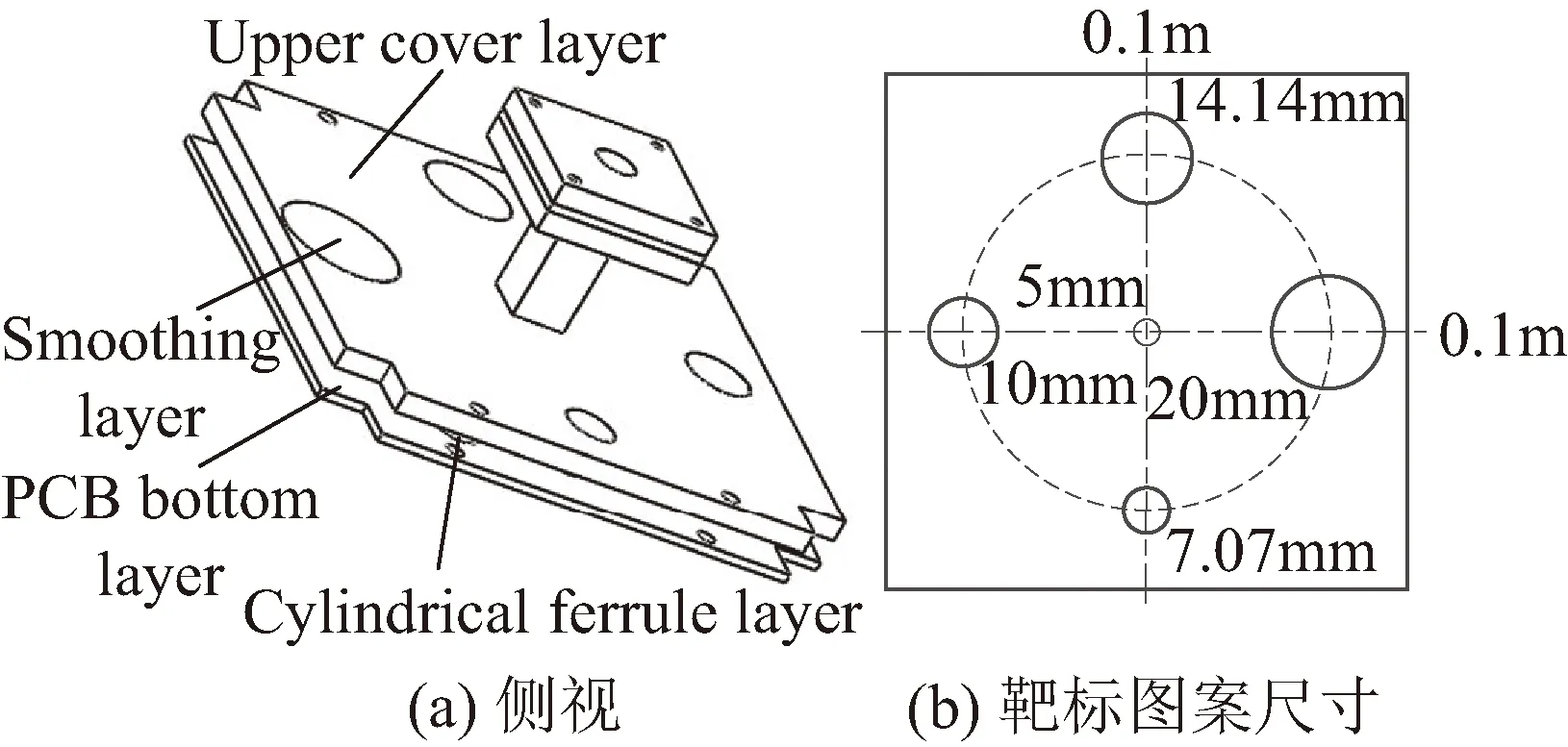
图1 多层立体靶标Fig. 1 Mutil-layer stereo marker

该立体靶标的尺寸为98 mm×98 mm×30 mm，由5个不共面的、发光波长为850 nm的LED灯组成。立体靶标分为4层结构，从下至上分别为PCB底板层、圆柱套圈层、上盖板层和修光层。PCB底板层的作用是按照设计图案将贴片封装类型的LED 灯摆放在相应的区域,如图1(b)所示，每个圆圈代表一个LED灯。圆柱套圈层的作用是将LED灯发出来的光限定在特定区域，圆柱套圈内径大小和设计的图案尺寸一致，满足16∶8∶4∶2∶1的关系，作为立体靶标的数字编码信息。上盖板层具有结构安装和支撑的作用。修光层选用的是聚酰亚胺薄膜，可将LED灯发出的光修整为一个规则的圆形光斑。

1.2 相机选型

考虑到立方星体积、质量和功耗有限，且空间中其他的干扰光源大部分来自可见光波段。为了排除其他光源的干扰，将相机的成像范围设定在红外波段，且立体靶标上的LED灯的发光波长为850 nm，所以选择支持红外波段成像的微型相机对立体靶标进行成像。该微型相机的主要参数如表1所示。

表1 微型相机主要参数

1.3 有无红外窄带滤镜的图像获取性能测试

空间光照条件复杂多变，太阳和地球有时也会出现在相机视野中，此外，航天器表面会产生强反射光的现象，这些都会导致靶标图像质量恶化。为了保证靶标图像质量，避免杂散光和背景的干扰，针对立体靶标采用波长为850 nm的LED光源，在相机镜头处添加仅通过850 nm波长光的红外窄带滤镜。

为测试视觉传感器系统性能，我们搭建可模拟航天器在轨实际光照条件的实验系统，对该视觉传感器系统进行图像获取性能测试。主要考虑两种可能出现的情况：

1) 太阳出现在相机视场且卫星表面发生强反射光的情况；

2) 地球出现在相机视场且卫星表面发生强反射光的情况。

测试效果如图2所示，其中图2(a)(c)为有红外窄带滤镜的两种情况下获取的靶标图像。图2(b)(d)为没有加红外窄带滤镜的靶标成图像。对比图2(a) (c)和图2(b) (d)可见，配备红外窄带滤镜的微型相机可以滤除强反射光和背景光的干扰。

图2 两种情况下的图像获取测试Fig. 2 The test of image acquisition in two cases

2 相对位姿求解

相对位姿求解包括图像处理和相对位姿估计。下面将分别阐述相对位姿求解涉及的图像处理和相对位姿估计的IDS算法。

2.1 图像处理

图像处理需要将靶标图案从背景中分离出来，并进行图案区域的中心点定位，以作为IDS位姿估计算法的输入。图3给出了图像处理流程。

图3 相对位姿估计的图像处理流程Fig. 3 The flow chart of image processing for relative pose estimation

图像处理包括图像去噪、图像二值化、立体靶标5点图案提取以及图案匹配和中心定位。图像去噪采用维纳滤波法去除相机成像过程产生的噪声点。图像二值化采用自适应阈值二值化法，将采集的灰度图按照阈值大小转化为二值图像。立体靶标5点图案提取采用椭圆检测法将立体靶标对应的5个区域提取出来。该椭圆检测法分两步进行,包括初步椭圆检测和基于相似性的精确椭圆检测。

(1) 初步椭圆检测

设某轮廓的边缘点坐标为L={(xi,yi),1≤i≤n}，n为它的边缘点个数，那么它包含的区域面积为：

(1)

假设轮廓边缘上任意两点ai(xi,yi)与aj(xj,yj)之间的距离为dai,j：

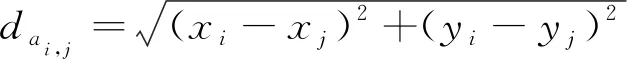
(2)

从边缘点中搜寻最左端点a0，最右端点a1，最上端点a2，最下端点a3，它们两两之间的距离中的最大值的一半为该轮廓外接圆半径R：

(3)

在得到了轮廓边缘的一些属性后，可以利用直接最小二乘椭圆拟合方法[13]来对所有轮廓进行初步椭圆检测，从而得到图像中所有的椭圆轮廓。

(2) 基于相似性的精确椭圆检测

初步椭圆检测可以得到图像中所有的椭圆轮廓，但是里面仍然存在不属于立体靶标的椭圆轮廓，需要利用同一靶标上轮廓相似性进行精确检测。根据Hu不变矩理论[14]中的边缘形状不变矩的特性，设计了图像中立体靶标的5个椭圆轮廓的精确检测方法。该方法计算了所有初步检测出的椭圆轮廓的相似性因子，通过相似性因子的大小来对椭圆轮廓进行取舍，保留最相似的5个椭圆轮廓。该方法的初步实验测试结果见图4。其中图4(a)为原始图像，该图像中有5个形状相似但大小不同的椭圆轮廓属于同一靶标，另外2个椭圆轮廓不属于该靶标。图4(b)为去除其中一个不相似的椭圆轮廓。图4(c)为只有靶标的5个椭圆轮廓。

图4 基于相似性的椭圆轮廓精确识别方法测试Fig. 4 The test of precise identification method of elliptical contours based on similarity

在该初步测试的基础上，将测试样本增加至3 000个，并采用相同的方法对图像中属于靶标的图案进行提取。实验结果显示，有2 993个样本可以将属于靶标图案的5点区域提取出来，提取成功率为99.98%。如果没有成功提取靶标图案的5点区域，则将图片舍弃。

后面的图案匹配是将设计的靶标图案与成像后的图像区域对应起来，本文采用多层立体靶标的数字编码信息进行图案匹配。最后采用灰度重心法对提取的5个区域进行中心定位。

2.2 相对位姿估计的IDS算法

(1)初步相对位姿估计

立体靶标上一点h在世界坐标系中的三维坐标(Xh,Yh,Zh)与对应的像素坐标(u,v)具有如下关系：

(4)

式中：Zc为未知的比例因子；f为相机焦距；dx和dy为图像像素的物理尺寸；R和T为世界坐标系与微型相机坐标系之间转换的旋转矩阵和平移矢量，R∈R3×3，T∈R3×1。

由于微型相机坐标系和立体靶标坐标系之间存在相对俯仰角和相对偏航角，导致靶标上的圆形图案在成像后发生变形，成为近似椭圆形的光斑。假设5个椭圆光斑的中心点坐标分别表示为(ua,va)，(ub,vb)，(uc,vc)，(ud,vd)和(ue,ve)。(up,vp)表示图像中共面的4个椭圆光斑的中心点坐标。

相对俯仰角θ和相对偏航角ψ可以使用非共面点偏离共面4点中心的距离来表示：

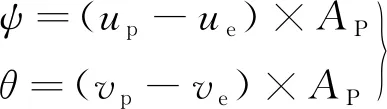
(5)

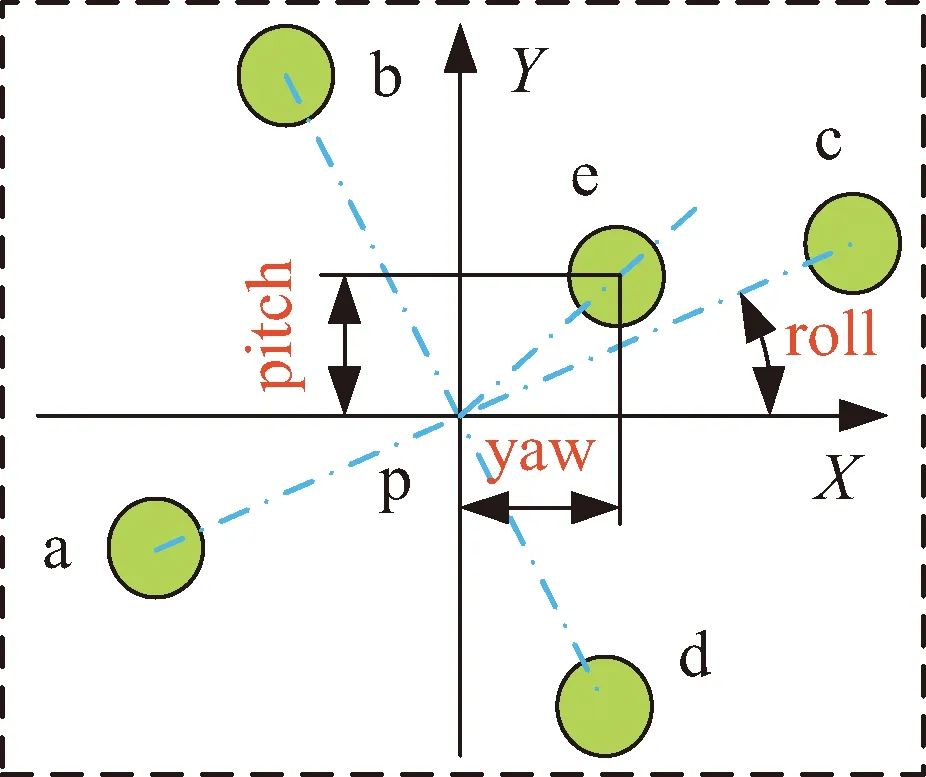
图5 相对位姿估计方法示意Fig.5 The schematic diagram of relative pose estimation method

式中：AP为相机的角分辨率。如图5所示，pitch表示相对俯仰角，yaw表示相对偏航角，roll表示相对滚动角。相对滚动角用符号φ表示，使用图案a的中心点坐标(ua,va)和c的中心点坐标(uc,vc)所连接的直线与图像物理坐标系的正X轴方向的夹角表示。

深度方向上的相对距离由下式进行估计：

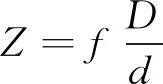
(6)

式中：D为图案a的中心点和c的中心点连线的实际物理尺寸；d为图案a的中心点和c的中心点连线的成像尺寸；Z为相机距离立体靶标在深度方向上的相对距离。

由于式(6)没有考虑相对姿态角对图案a的中心点和c的中心点连线的成像尺寸的影响，如果直接按式(6)计算微型相机和立体靶标在深度方向上的相对距离，在相对姿态角较大的情况下，由式(6)获得的距离误差会增大。本文考虑相对姿态角对深度信息Z的影响，将式(6)修正为：

(7)

式中：d=(ku|ua-uc|dx)/cosφ；ku为相对偏航角对深度信息Z的补偿系数，它补偿了相对偏航角对靶标图案a的中心点和c的中心点连线在成像后造成的变形影响。ku采用相对偏航角的余弦值近似替代：

ku=cosψ

(8)

将式(8) 带入式(7)中，根据针孔成像模型，求解出微型相机和立体靶标之间的初始相对位置为：

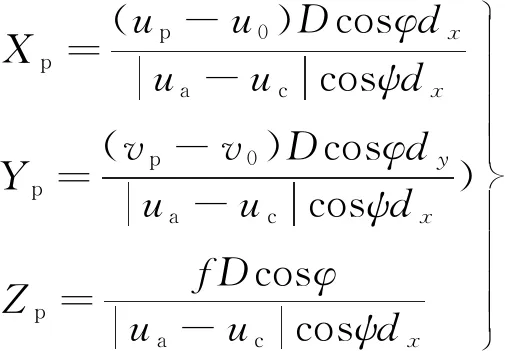
(9)

(2)基于Haralick迭代算法的位姿优化

通过式(4)～(9)可求出微型相机坐标系和立体靶标坐标系之间的初始相对位姿。然后，采用Haralick迭代算法[15]优化初始测量结果。由于图像处理过程中存在误差，使得目标特征点不在成像点的逆投影线上。因此，利用该误差定义如下目标函数作为相对位姿测量结果的评价准则。

(10)

式中：t=(tx,ty,tz)T和M分别为立体靶标坐标系相对于相机坐标系的平移矢量和旋转矩阵；si为立体靶标上的5个图案中心点在立体靶标本体坐标系中的坐标，即{si:(xi,yi,zi),i=1,2,…,5}；di为立体靶标上的图案中心点距离相机投影中心的景深，

di=(Msi+t)Tvi,i=1,2,…,5

(11)

式中：vi为图案中心点在逆投影线上的单位矢量，

(12)

然后求出立体靶标上的5个图案中心点在立体靶标本体坐标系和利用景深求出的坐标平均值分别为：

(13)

(14)

定义协方差矩阵C为：

(15)

对C进行奇异值分解：

C=UΣVT

(16)

式中：U和V为酉矩阵；Σ为一个对角矩阵。得到旋转矩阵M和平移矢量t为：

M=VUT

(17)

t=-MμA+μB

(18)

位姿优化问题可以描述为：

(19)

其中旋转矩阵MMT=I。

为了使目标函数值ε2减小，引入梯度最陡下降法[16]对式(19)求偏导，并令其为零得到：

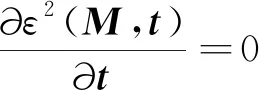
(20)

进而可得：

(21)

将t带入式(18)，求出新的M值。重复式(18)～(21), 并将求出的结果带入式(10)，求得第k次的目标函数为：

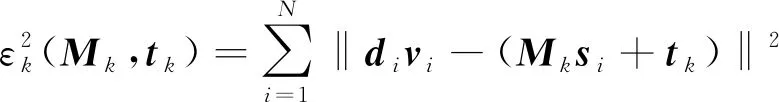
(22)

迭代终止条件设为：

(23)

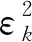
当误差收敛后，得到立体靶标坐标系和相机坐标系之间的相对位姿为：

(24)

最后根据立体靶标和微型相机在卫星中的安装位置关系，得到服务星本体坐标系与目标星本体坐标系之间的相对位姿。

3 实验校验

3.1 实验方案

为了测试该视觉传感器的性能，搭建了图6所示六自由度地面实验系统。

图6 地面实验系统Fig. 6 Ground experiment system

该实验系统包括三轴转台、三自由度导轨、支持红外波段成像的微型相机、立体靶标、太阳模拟器和地球背景等。三轴转台和三自由度导轨分别作为旋转运动模拟器和平移运动模拟器。太阳模拟器用于模拟真实的空间光照环境。此外，校验实验完全在暗室中进行，排除了其他光源对实验结果的影响。

在实验过程中，微型相机和立体靶标之间的相对位置和姿态的运动轨迹完全按照服务星和目标星在轨道上的真实相对运动模型进行设计，其中相对位置的运动模型采用Clohessy-Wiltshire (C-W)方程[17]，相对姿态的运动模型采用姿态动力学和运动学组合模型[18]。

为校验所设计的视觉传感器的位姿测量性能，考虑两种情况下的位姿测量精度：

1) 在不同距离处，视觉传感器的相对位姿测量精度。试验测试距离通过三自由度导轨从2.5 m移动至0.6 m处，每隔0.1 m采样一次。

2) 在不同相对姿态角处，视觉传感器的相对位姿测量精度。试验过程中的相对滚动角通过三轴转台从0°旋转至40°处，每隔2°采样一次。

为了验证所提出的IDS算法的性能，采用经典的P3P算法和EPnP算法同IDS算法进行比较。

3.2 实验测试与结果分析

实验测试结果如图7～图10所示，显示了不同算法在该视觉传感器中的测量误差。

从图7和图8可以看出，随着距离增加，相对位姿估计算法的精度会降低。在相对距离为1 m时，IDS算法在深度方向上的精度约为1.77 mm，横向精度高于深度方向，分别为0.22 mm和0.18 mm。相对滚动角的精度为0.07°，相对偏航角和相对俯仰角的精度分别为0.33°和0.37°。另外，比较3种相对位姿估计算法在图7和图8中的实验测试数据可以看出，在不同相对距离处，IDS算法的测量精度要优于经典的EPnP算法和P3P算法。

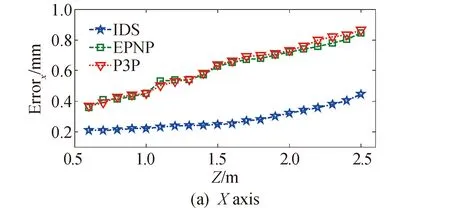
图7 不同距离处的相对位置估计精度Fig. 7 Relative position estimation accuracy at different distances

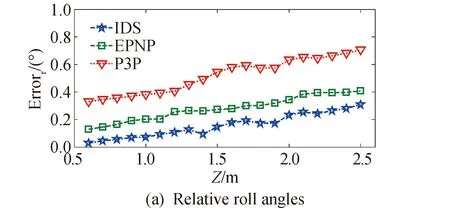
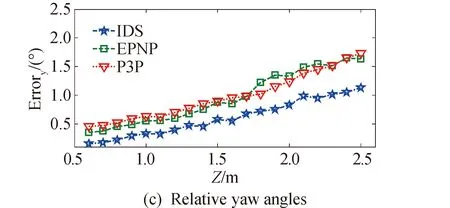
图8 不同距离处的相对姿态估计精度 Fig. 8 Relative attitude estimation accuracy at different distances

图9 不同相对姿态角处的相对位置估计精度Fig. 9 The Relative position estimation accuracy under different relative attitude angles

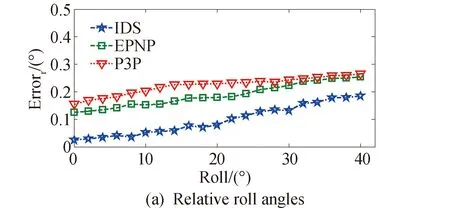
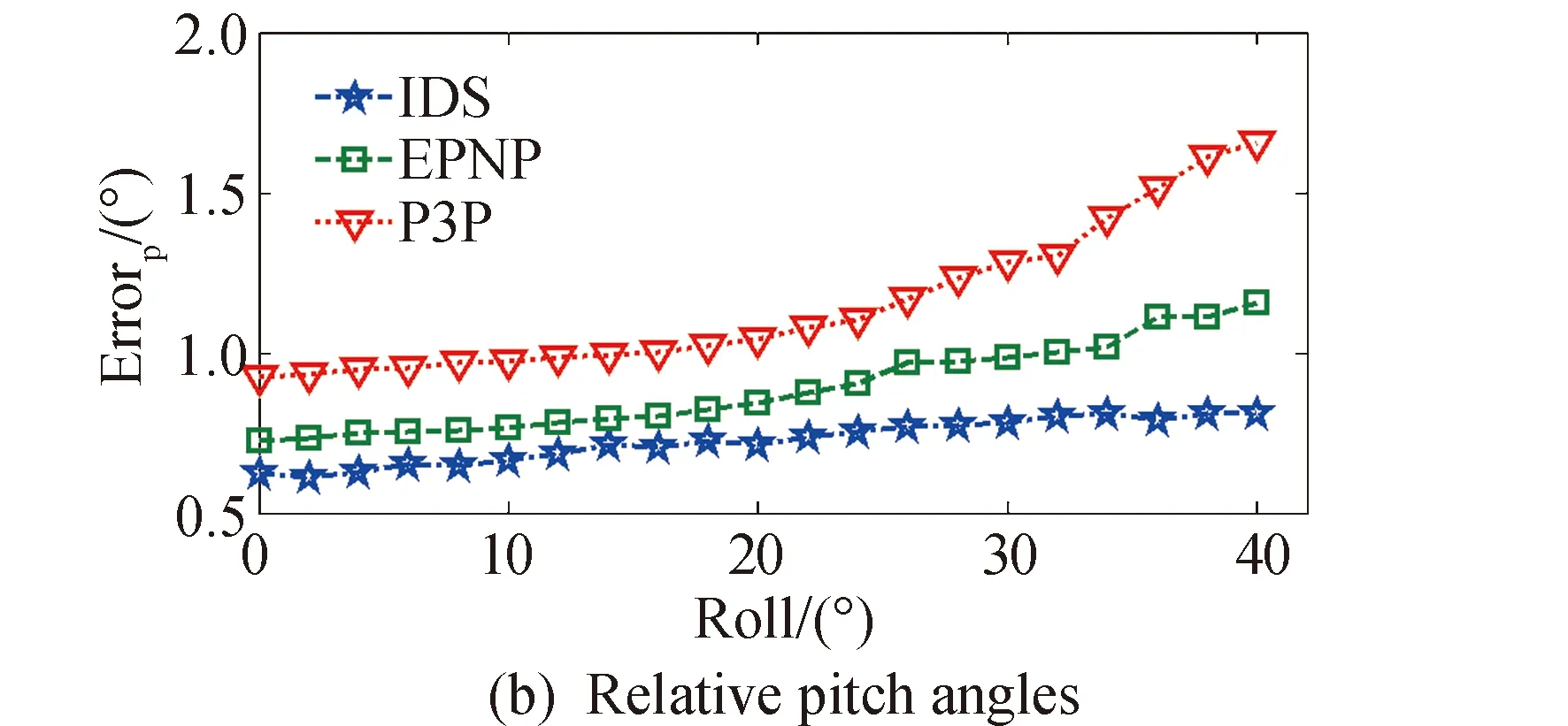
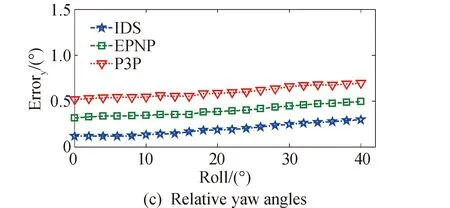
图10 不同相对姿态角处的相对姿态估计精度Fig. 10 Relative attitude estimation accuracy under different relative attitude angles

从图9和图10中可以看出，相对位姿估计算法的精度会随着相对姿态角的增大而略有降低。当相对姿态角中的滚动角为20°时，IDS算法的深度方向上的测量精度约为1.53 mm，横向上的测量精度分别为0.25 mm和1 mm。相对滚动角的精度为0.08°，相对俯仰角和相对偏航角的测量精度分别为0.18°和0.71°。另外，比较3种相对位姿估计算法在图9和图10中的实验测试数据可以看出，在不同相对姿态角处，IDS算法的测量精度要优于经典的EPnP算法和P3P算法。