利用BP神经网络对卫星无热敏设备温度的估测
2021-05-21宁东坡徐志明刘质加
宁东坡,徐志明,刘质加
中国空间技术研究院,北京 100094
随着航天技术的发展,小卫星在遥感、减灾、农业等方面的应用越来越广泛。卫星在太空中绕轨道运行,太空热环境恶劣,卫星主要会受到太阳辐射、地球反照和地球红外辐射外热源影响,因此必须进行专门的热控设计保障卫星正常工作[1]。
为监测卫星设备温度,热控设计中常在卫星设备上粘贴热敏电阻作为测温点,由于卫星的测温需要通过星务遥测通道采集,星务遥测通道有限,同时考虑到成本、质量等因素,只在卫星重要设备或者结构处粘贴测温点,因此遥测得到的测温数据有限,不能得到无测温点设备的温度。张旭东等[2]研究通过建立卫星在轨设备温度的解析解,利用神经网络预测当前时刻10 s后设备的温度,但是无法得到当前时刻温度,并且由于卫星实际存在漏热等多方面因素,解析解并不能精确估测。刘柏麟等[3]研究了设备温度与安装面之间的数学关系,基于传热学理论推导出计算设备温度公式,但是该算法依赖于空间外热流的变化,估测精度不高。张也弛等[4]研究了基于统计学方法根据几个遥测点来推断温度场,这种方法依赖于遥测点的位置。因此如何通过卫星上已有测温点的遥测数据去估测无测温点设备的温度急需研究。
近年来,机器学习方法在工程中的应用日益增多,在航天中的应用也十分广泛[5-7]。在本文基于反向传播(BP)神经网络优异的非线性系统拟合能力,提出利用BP神经网络来估测卫星无测温点设备在轨温度[8]。
1 BP神经网络介绍
1.1 BP神经网络的基本概念
BP神经网络全称是反向传播误差神经网络,对于复杂、难以用数学方法准确建模的非线性系统有着优秀的拟合能力[9]。BP神经网络接受多维数据的输入,通过输入层、隐含层、输出层,输出数据。输入数据和输出数据之间的内在映射关系通过各层神经元之间的连接权值和偏置量来体现。
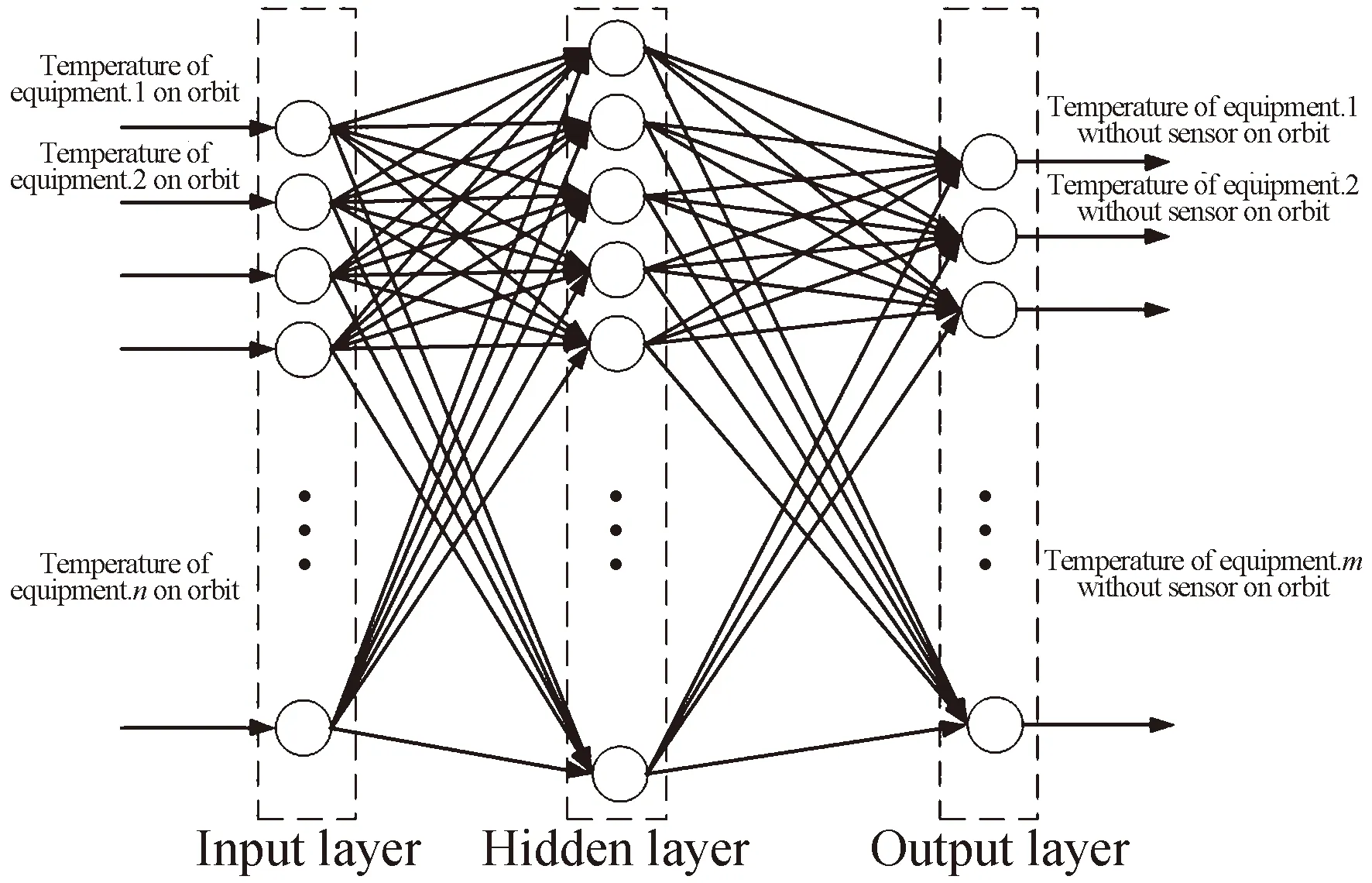
图1是一个18输入10输出的BP神经网络模型结构。Input为输入层,Output为输出层,中间是隐含层(Hidden)。BP神经网络由输入层、隐含层和输出层组成,层与层之间全连接,同一层之间的神经元无连接。输入值由输入层输入,正向流动。修正权值时,网络根据误差由后向前逐层修正网络的连接权值。随着学习的不断进行,最终误差越来越小。
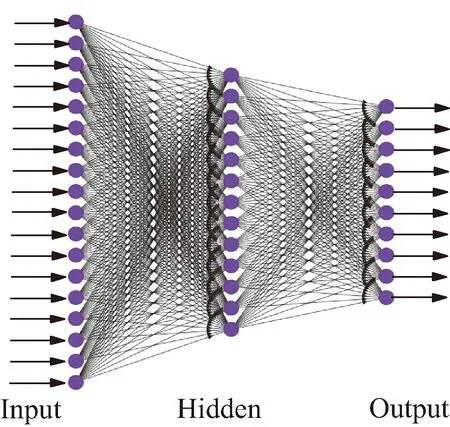
图1 BP神经网络结构Fig.1 Structure of BP neural network
BP神经网络的训练依赖于大量的样本训练,样本的集合代表性、矛盾样本多,则所训练后的神经网络容易欠拟合。所以训练时应选择多样性、数据量足够的样本[10-11]。
1.2 BP神经网络的应用
BP神经网络广泛应用于预测、压缩、分类等领域,在实际应用中,大约80%的神经网络模型采取了BP神经网络模型。热网络系统是一个各设备温度高度耦合的系统,不同设备温度之间存在互相影响,影响的大小就体现在BP神经网络模型神经元之间的权值上[10]。使用BP神经网络拟合卫星热网络系统过程就是不断寻找能够逼近拟合该卫星设备温度的BP神经网络模型神经元的权值和偏置值的过程。BP神经网络在学习过程中先随机初始化权值和偏置值,然后通过反向传播算法调整权值和偏置值,最终达到设定误差后,获得最后的权值和偏置值[11]。
2 估测思路
卫星测温一般通过热敏电阻(以下称测温点)来测温,星务采集热敏电阻的信号,转化成温度并通过天线传到地面。热控分系统设计时一般会在高热耗设备或者有主动加热回路设备粘贴热敏电阻,获取温度。一些热耗较小或者常用的继承性设备不粘贴热敏电阻。
∑Dij(Tj-Ti)+qin+qout
(1)
式中:ci为节点i的比热容;Mi为节点i的质量;Ti为节点i的当前温度;t为时间;Eij为节点i和节点j之间的角系数;Dij为节点i和节点j之间的接触传热系数;qin为星内热耗;qout为外热流[8]。
如式(1)所示,卫星内的温度场是外热流与内热源综合作用的结果,每个设备与周围设备和环境通过辐射换热和导热进行热交换,热交换带来了温度的变化。在卫星热试验时,为了获取更多温度数据和校准热敏电阻测温,通常在卫星上粘贴大量的热电偶。热电偶成本低,粘贴简单。热电偶粘贴的位置根据热控设计需要,在有热敏的设备与一些无热敏的设备上都会粘贴热电偶,热试验后会将所有热电偶拆除。
热试验一般是热平衡试验和热真空试验[9]。热试验中外热流和内热源变化形式较多,所得到的温度数据变化范围大,具有多样性。在热试验中会得到热敏电阻的数据和无测温点上设备热电偶数据。因此可以通过BP神经网络,以热敏电阻温度数据为输入,无测温点设备上的热电偶温度数据为输出,训练神经网络,建立起卫星的估测神经网络。当在轨飞行时,以遥测的热敏电阻温度数据为输入,去估测无测温点设备的温度。
3 建立BP神经网络模型
3.1 样本数据采集和预处理
在热试验中除了热敏电阻以外,星内粘贴了大量的热电偶。热平衡试验是在星外加载稳态外热流,星内设备按照工作模式工作。热真空试验是通过调节卫星外热流和设备开关机使得设备温度达到工作温度的高低温极限附近。图2给出3个设备在热试验过程中温度变化情况。
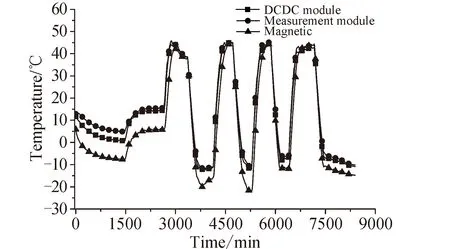
图2 热试验中设备温度曲线Fig.2 Temperature profiles of equipment of satellite in thermal test
从图2可以看出卫星在热试验期间设备温度变化范围比较广,数据量大,具有广泛性的特点。
如图3所示,设备温度在0~1 470 min为卫星热试验低温工况,设备温度较低,在1 470~2 660 min为高温工况,设备温度上升到较高水平。2 660 min到最后试验结束,处于高低温循环过程,设备温度变化较为剧烈。
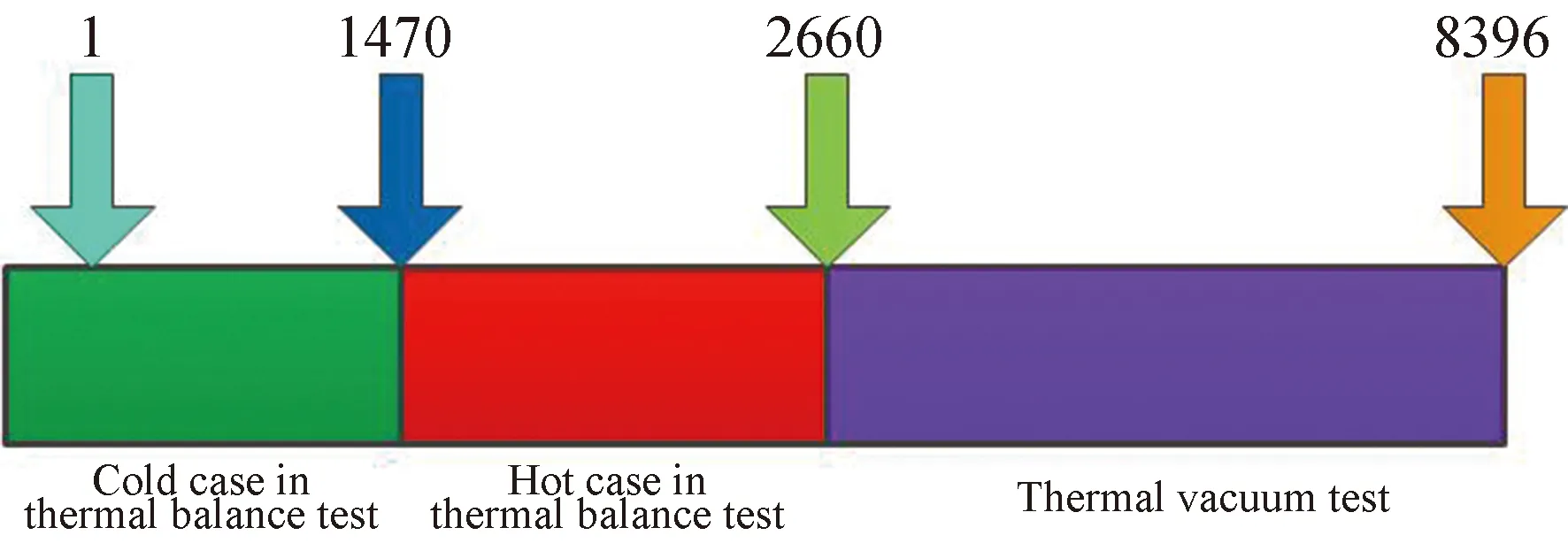
图3 样本数据在热试验中的分布Fig.3 Samples distribution in thermal test
为了减少各维数据间数量级差别,避免因为输入/输出数据数量级差别较大造成网络估测误差较大,必须将样本数据进行归一化处理。将输入/输出值通过归一化处理映射到[0,1]之间,归一化采用以下公式:
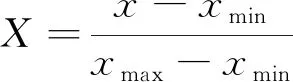
(2)
式中:X为归一化后的数据;x为原始数据;xmin和xmax为原始数据中的最小值和最大值。
3.2 BP神经网络建立
BP神经网络的建立主要包括样本数据采集、神经网络训练等步骤。本文所研究的卫星样本数据中共有25个星内设备,其中18个设备粘贴有热敏测温点,将其作为输入层,7个设备无热敏,但是在热试验中有热电偶数据,将其作为输出层。隐含层的节点数对神经网络的估测精度影响很大,节点数少会欠拟合,节点数多会过拟合。一般参考如下公式选取(公式之间相互独立):
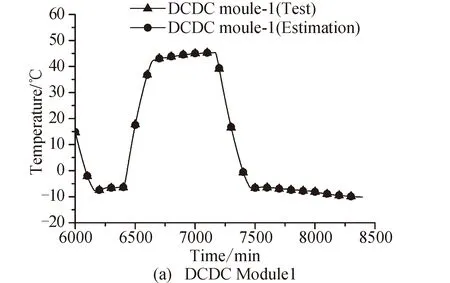
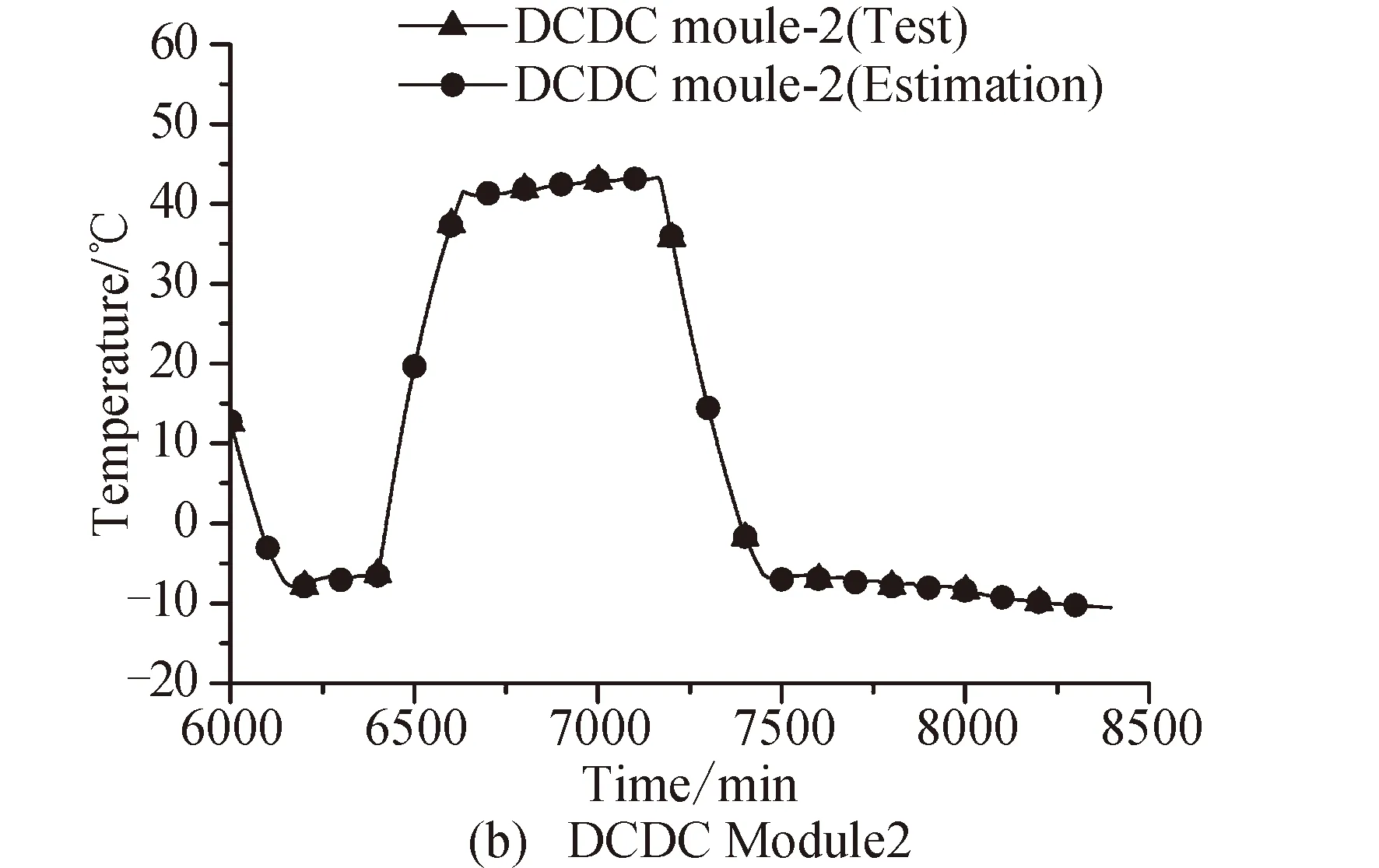
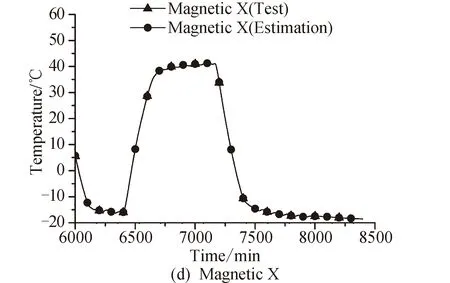
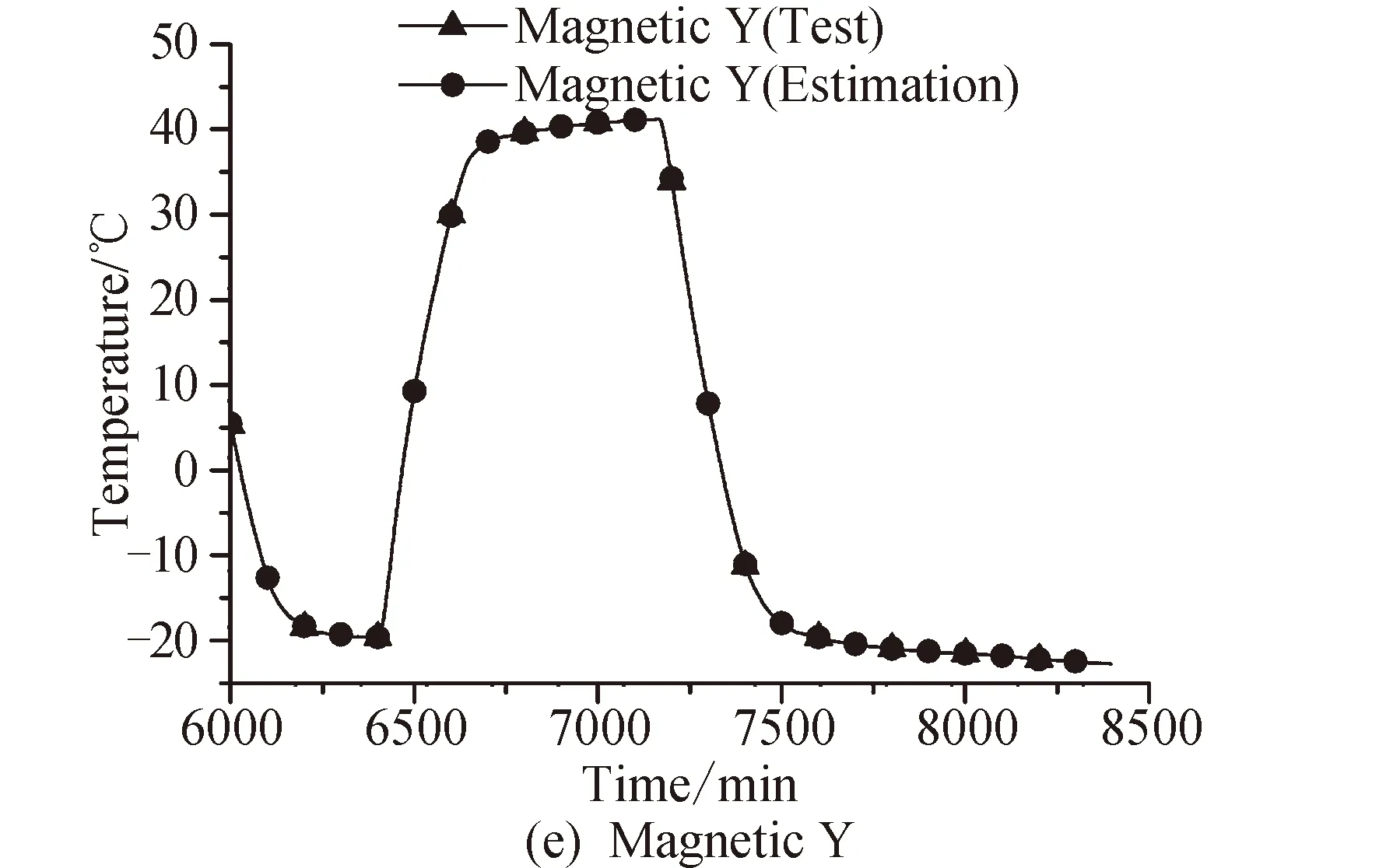
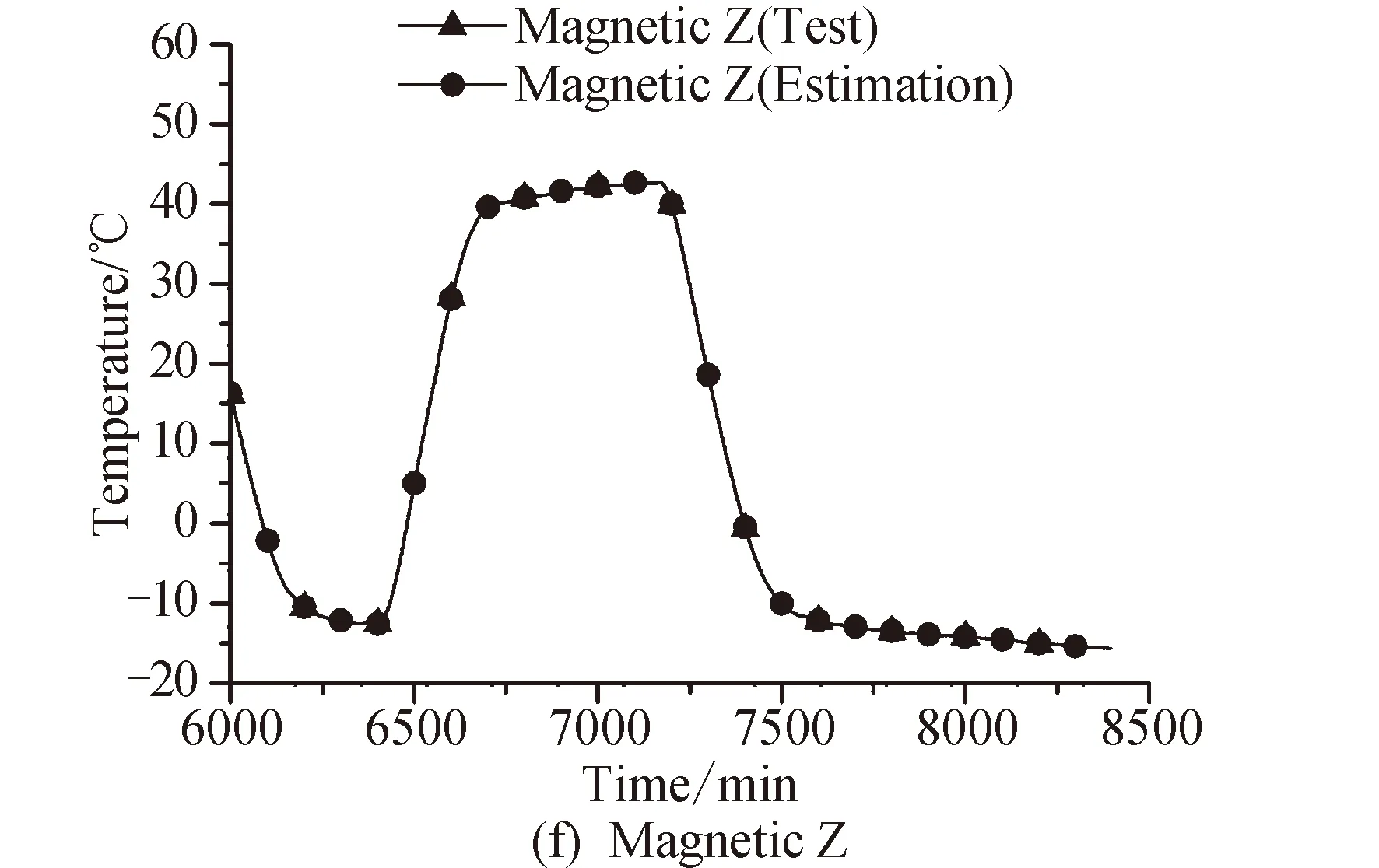
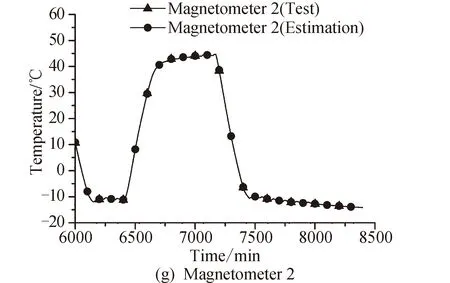
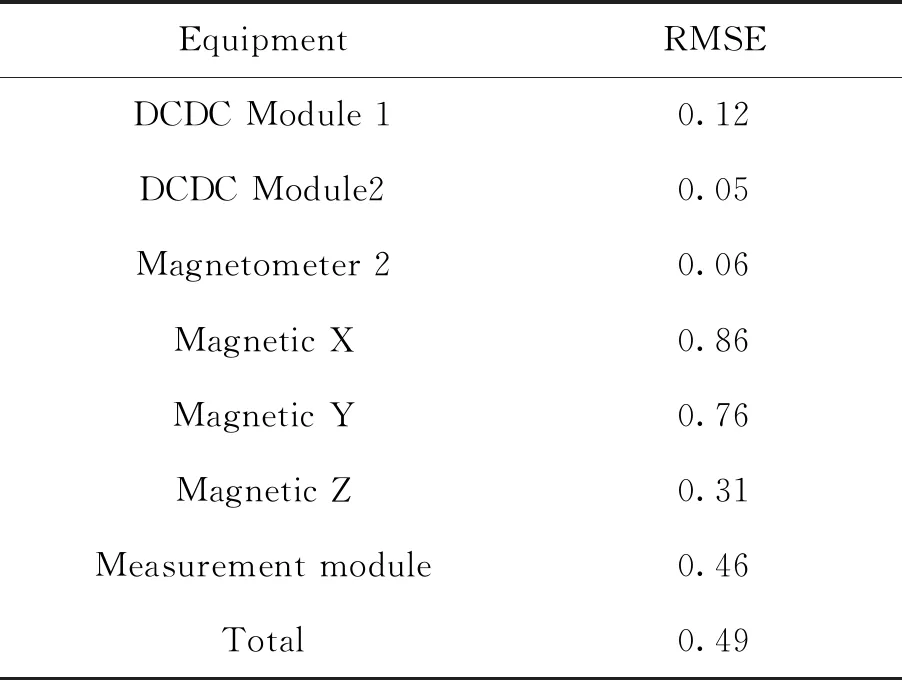
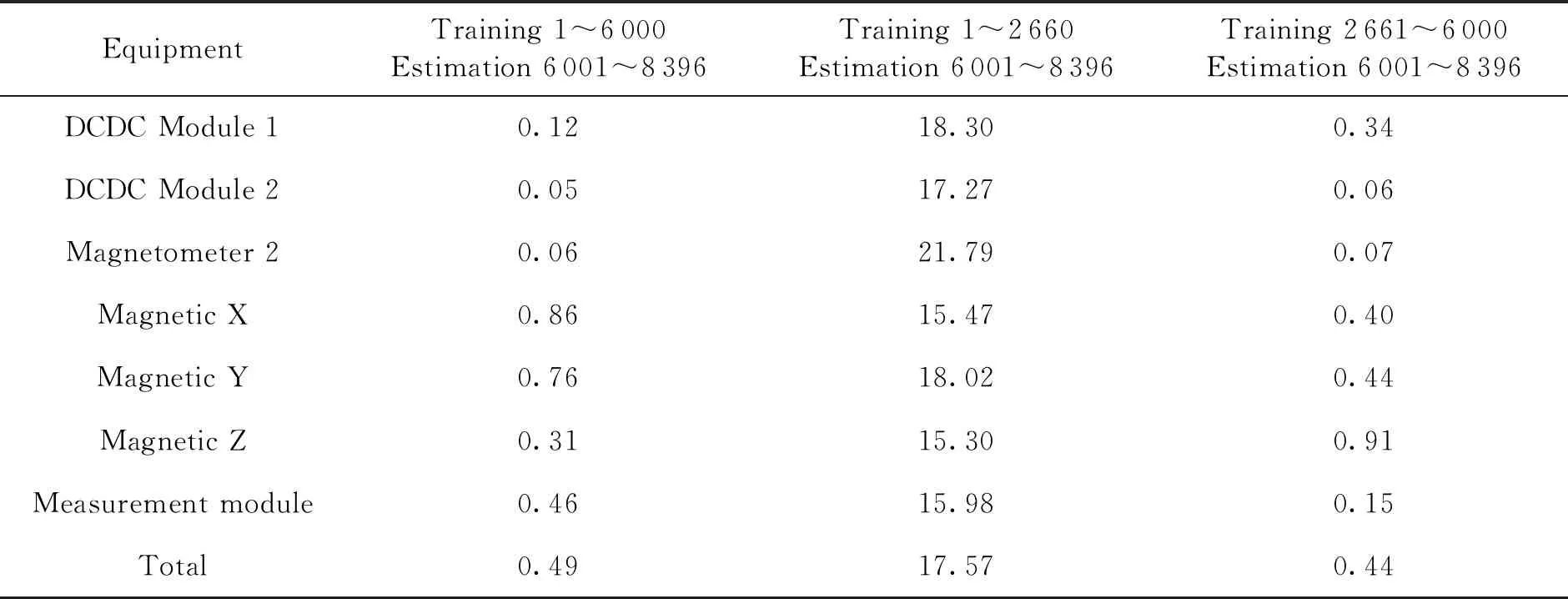
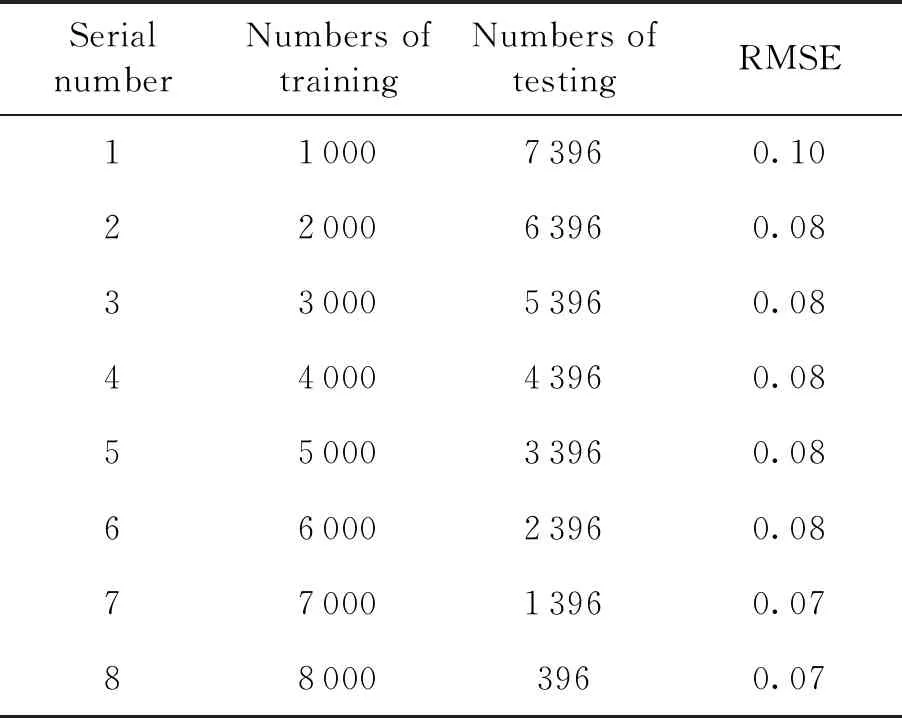
l (3) (4) l=log2n (5) 式中:n为输入层节点数;l为隐含层节点数;m为输出层节点数;a为0~10之间的常数。 隐含层节点数的选取并没有数值解[12],式(3)~(5)也只是参考。本文参考上述公式推荐的数值范围,并且计算了隐含层节点数6~20之间的神经网络估测误差,综合考虑取隐含层节点数为13。 建立的星上无测温点设备温度估测神经网络如图4所示。星上设备在轨遥测数据作为输入层,通过所建立的神经网络拟合,可得到无测温点设备的温度。 图4 温度估测神经网络结构Fig.4 Structure of neural network for temperature prediction 在热试验中样本数据共采集了8 396 min,每分钟记录一组28个设备的温度值,所以共有8 396组有效数据。将样本数据分为两部分,一部分为训练集,一部分为测试集。前6 000 min采集的6 000组数据为训练集,后2 396 min采集的2 396组数据为测试集数据。用训练集的数据训练所建立的神经网络。 BP神经网络在初始会随机生成权值初始值,在后面迭代中根据误差不断的更新权值,这样会造成所建立神经网络的不可重复性。为了尽可能提高训练精度,将训练误差目标值设为1×10-6,当达到训练精度,自动保存神经网络文件。 为了验证所建立的神经网络 ,采用所建立的神经网络估测了热试验数据6 001~8 397 min无热敏的设备的温度。并把估测值和试验值进行了对比。 图5是7个设备的试验值和神经网络估测值的曲线。可以看出这7个设备的估测值和试验值几乎完全重合。这说明训练后的神经网络估测精度很高。 图5 神经网络估测值与试验值对比Fig.5 Comparison between predicted and measured values 续图5Fig.5 Continued 为评价网络模型估测结果的精确程度,引入均方根误差性能函数来评价神经网络模型[13]。均方根误差计算公式为: (6) 式中:b为估测数据与真实数据差值;N为测试集数量。 均方根误差是预测值与真实值偏差的平方与预测次数比值的平方根,常用来作为机器学习模型预测结果衡量的标准。经过计算,对7个设备温度估测结果的均方根误差见表1。 从表1中可以看出所有设备估测结果的均方根误差均小于1,估测精度很高。 表1 估测结果的均方根误差 本文第3节和第4节中所采取的神经网络模型训练数据用的是热试验前6 000 min采集的6 000组数据,后2 396 min采集的2 396组数据为测试集数据。而2 660~8 396 min都是热真空试验,设备温度变化相似,都是为高低温循环。为了研究训练集对估测结果的影响,进行了不同训练集对估测结果的影响分析。 分别选取了训练集为样本数据中1~2 660组数据,估测样本数据中6 001~8 396组数据,训练集为样本数据中2 661~6 000组数据,估测样本数据中6 001~8 396组数据,并与第3节和第4节估测的算例进行比较。这3个算例的估测结果均方根误差见表2。 从表2可以看出,上述3个算例的估测集都为样本数据中6 001~8 396组数据,而训练集为1~6 000组数据和2 661~6 000组数据时估测精度接近,当训练集为1~2 660组数据时,估测精度非常低。分析认为,训练集样本的多样性对估测结果影响很大,BP神经网络模型的逼近能力与学习样本的典型性和多样性密切相关,如果样本的集合代表性差、矛盾样本多、存在冗余样本,网络就很难达到良好的逼近能力。如果训练集只是1~2 660组数据(热平衡试验数据),无法覆盖热真空试验的数据特征,因此训练的BP神经网络模型对6 001~8 396组数据(热真空试验数据)估测精度较低。 表2 估测结果的均方根误差 神经网络类似于人的学习过程,只有当训练集足够多,并且覆盖多种场景,训练出的神经网络模型才能够估测精度高。 从8 396组数据中随机抽取若干组数据作为训练集,以样本集中除训练集外的数据为估测集,测试所建立的BP神经网络模型估测性能。其均方根误差如表3所示。 表3 训练集无关性测试结果 从表3可以看出,随机抽取训练集训练出的神经网络模型估测无测温点设备温度的均方误差仍然很小。并且随着训练集数目的增加,均方误差向减小趋势发展(由于神经网络模型初始值的随机性,估测的均方误差略有偏差,但是不大)。 值得指出的是,训练集的多样性[14]对神经网络模型的估测精度有着明显的影响,覆盖多种场景的训练集能够使得神经网络模型得到更加充分的训练。为了与表2中训练集数量进行对比,从样本数据中随机抽取了50个数据作为训练集,用其训练的神经网络模型估测温度的均方误差为0.498 3,远远大于表2中的估测精度,说明了神经网络模型训练集选择的重要性。 本文提出一种使用机器学习方法即BP神经网络模型来估测星上无测温点的设备温度方法。结果表明,利用热试验获得的热敏电阻和热电偶的温度数据训练的BP神经网络能够准确估测无测温点设备温度,测试结果显示估测精度在1℃以内。BP神经网络模型估测温度的误差大小与学习样本的多样性和数据量相关。本文利用BP神经网络估测温度的方法不仅提供了一种获取星上更多设备温度的手段,而且能够节省测温资源。后续将根据卫星热网络系统特点,以BP神经网络为基础,研究复杂网络模型在估测卫星设备温度方面的应用。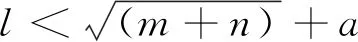
3.3 BP神经网络训练
4 温度估测
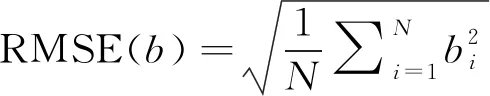
5 训练集对估测结果的影响分析
6 结束语
