基于MapReduce的相似矩阵并行构造
2021-05-20罗莉霞蒋盛益
罗莉霞,蒋盛益
(1.湖南信息学院 电子信息学院,湖南 长沙 410151;2.广东外语外贸大学 信息科学与技术学院,广东 广州 510006)
0 引 言
推荐系统基于用户行为大数据,根据用户的个性化需求提供多种多样、有针对性的解决方案[1]。其中,基于相似矩阵构造的协同过滤算法的性能高低直接决定了推荐系统的推荐精度、响应速度等关键性能[2]。因此,设计高性能的协同过滤推荐算法引起了研究人员的极大关注。
现有研究往往基于传统串行平台展开。文献[3]提出一种基于实值的状态玻尔兹曼机的协同过滤算法,但受限于合理状态转移过程的设计。文献[4]提出基于半监督方法的协同过滤推荐算法,但存在半监督机制全局最优解求解困难的问题。文献[5]将差分隐私保护技术引入协同过滤中,但没有绝对的隐私泄露保护,如何根据系统的变化升级,实现保护手段的及时跟进仍是一个需要解决的问题。推荐系统的性能不仅仅受限于协同过滤算法的设计,更受制于巨维数据下协同算法中相似矩阵的构建精度[6]。
基于上述分析,针对广泛在推荐系统中应用的基于项目(item)的协同过滤推荐算法,提出一种MapReduce框架下的相似矩阵构造方法。主要创新点在于:
(1)所提方法由于在分散的有限资源计算节点上进行,摒弃了传统串行构造方法性能依赖于物理硬件性能的缺点,故而在大规模数据集场景下具有更好的经济性与扩展性。
(2)提出一种改进的局部敏感哈希(locality sensitive Hashing,LSH)算法对项目集进行快速相似性划分,与传统Hash算法相比,所提算法能够使相似集合有更高的概率被归为一类,从而提升后续轮次的计算效率。
1 总体架构与基本概念
1.1 总体架构
基于项目的协同过滤推荐算法的基本思想为:①利用数理统计的方法,首先寻找与目标项目具有相近评分的邻居项目;②对邻居项目进行评级打分,并依据评分结果对目标项目的评分进行预测;③推荐系统选择评分预测结果最高的前若干项作为推荐结果发送给目标用户[7]。因此,如图1所示,所提基于MapReduce框架的相似矩阵构造方法总体包含如下3个部分:

图1 所提方法总体架构
(1)项目集合分解。为提升相似矩阵计算效率,基于LSH算法将不同用户具有相似评分的项目划分为同一组,构成子项目集合,并将不同的项目子集分配到不同的计算节点中。此过程对应于MapReduce第一轮次计算。
(2)子项目集合内部相似度计算。基于Pearson相似性度量计算各子项目集合的相似矩阵。此过程对应于MapReduce第二轮次计算。
(3)子项目集合间相似度计算。基于Pearson相似性度量计算各子项目集合间的相似矩阵。并与第二轮次计算结果整合输出最终的相似矩阵。此过程对应于MapReduce第三轮次计算。
为便于后续算法设计步骤介绍,本节对相关基本概念进行必要的解释与说明。
1.2 MapReduce
MapReduce作为一种分布式并行处理平台,底层使用Hadoop分布式文件系统(Hadoop distributed file system,HDFS)可将大型文件划分为若干个片段,以冗余的方式存储于分散的多台计算节点中,提高系统可靠性[8]。而MapReduce 完整的运行过程则包含三阶段:映射(Map)、混洗(Shuffle)、归约(Reduce)[9]:
(1)在Map阶段,映射函数将键值对(key1,value1)作为输入,执行初步计算并输出中间键值对(key2,value2);
(2)在混洗阶段,对中间键值对进行分组,每个计算节点都被分配了相应的数据列表(key2,value_list);
(3)在Reduce阶段,任务跟踪器调用带有键和值列表的reduce函数,每个reduce函数执行值列表的计算,并发出键值对(key3,value3)作为最终结果。
1.3 改进的局部敏感哈希(LSH)算法
为快速衡量两个集合的相似度,传统手段采用局部敏感哈希(locality sensitive Hashing,LSH)算法进行度量。其基本原理为,对于相似的若干个对象赋予更高的碰撞概率,从而具有更高的可能性将它们归类到同一个Hash“桶”中。换言之,对于不相似的那些对象则具有更高的过滤概率从而节省计算时间以提高效率。传统的LSH函数定义如下:
定义1 LSH函数:给定某一依赖于度量空间Q的Hash函数组H={h∶P→U}, 其表征了点域P到某整数域W的一组映射函数。对于任意一个查询点p,若满足如下两个条件:
(1)若q∈B(p,r), 则Pr[h(p)=h(q)]>P1;
(2)若q∉B(p,r), 则Pr[h(p)=h(q)]>P2。
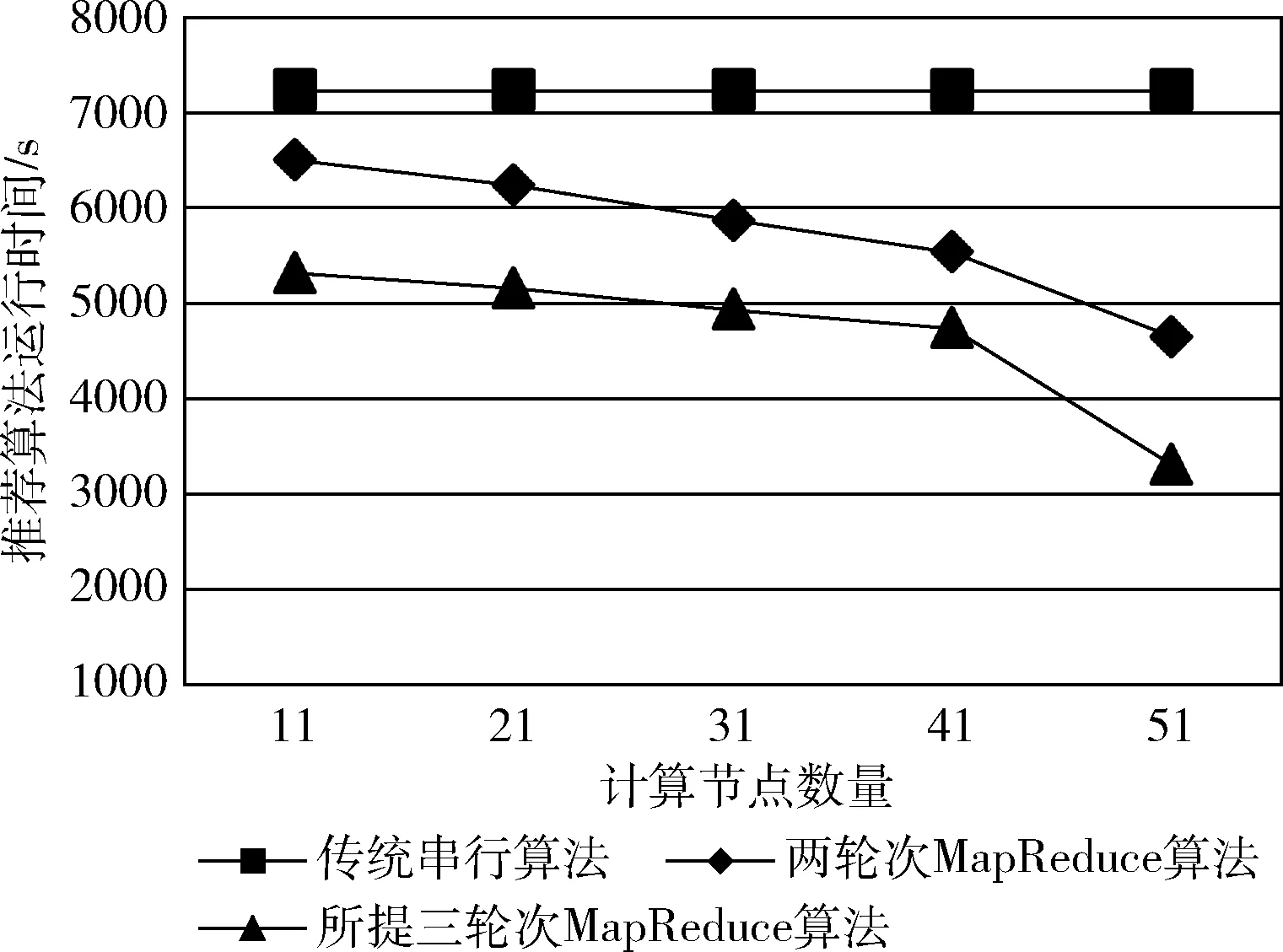
其中,B(p,r)={q|D(p,q)≤r} 表示r(>0) 为半径、以p为中心的球; Pr[·] 为概率算子;P1和P2为(0,1)内的正常数且满足0 选用基于P-稳态分布的LSH函数,首先给出P-稳态分布的定义: 定义2P-稳态分布: 对于包含任意N个元素的实数集合 {v1,v2,…,vN}⊆R和R上服从某一分布D的N个独立同分布变量T={t1,t2,…,tN}, 若随机变量∑l(vl·tl) 以及∑l(|tl|P)1/PT服从同一分布,则称D是P-稳态分布的,并且可以严格证明, ∀P∈(0,2] 均存在相应的稳态分布[10]。 根据上述定义,选择P-稳态分布的LSH函数为 (1) (2) 然而,根据式(1)和式(2)可知,传统LSH算法的性能依赖于Hash函数参数的选取,故而单次使用LSH算法对集合进行相似度区分易存在较高的碰撞概率,导致本质上不相似的数据集划分在一起,从而影响后续两个轮次MapReduce计算的效率。因此,提出一种改进的LSH算法,其核心在于在MapReduce框架下,应用传统LSH算法对用户项目集合进行多次Hash处理,从而使相似集合与不相似集合相比具有更高的概率归为一类,从而提升后续轮次相似矩阵的计算效率。主要步骤如下: (1)以均匀分布的方式随机选择k个Hash函数,构成维度为k的Hash函数组,记为Hk={h∶P→Uk}, 其中h(S)=[h1(S),h2(S),…,hk(S)]; (2)对数据集进行映射处理,从而得到数据集所对应的维度为k的Hash列表; (3)统计k次Hash操作的Hash值(记为K),设判定数据集相似的哈希阈值为ε。若K≥ε,则数据集是相似的;反之,若K<ε,则数据集是不相似的。 协同过滤推荐算法的核心在于构建“用户-项目”相似矩阵以实现精准的推荐。如图2所示,不妨设用户数量与项目数量分别为m和n,Rij为用户i(1≤i≤m)对项目j(即itemj,1≤j≤n)的评分。协同过滤推荐算法即是要构造出不同用户在同一项目上的相似性度量矩阵,不妨记为Sim(i1,i2),其中i1和i2为不同的用户编号。 图2 用户-项目评分列表 所提算法中,采用Pearson相关性进行来自于不同用户、对同一项目集合的相似性度量[11]。不失一般性,设用户i1和用户i2共同评分的项目集合为item(i1,i2), 从而用户i1和用户i2之间的Pearson相似性度量值为 (3) 为有效计算用户项目的相似性矩阵,所提基于MapReduce的相似矩阵并行构造方法包含3轮次的计算过程,即:①项目集划分;②子项目集内部相似度计算;③子项目集间相似度计算。 为计算不同用户在同一项目集合下的相似性,所提方法首先划分用户评分项目的评级列表。其基本思想是将类似用户评分的项目组合在一起,以便计算第二轮中这些子项目集合的相似性,从而减少最后一轮的计算开销。由于当项目集规模过大时对其采用传统诸如K-means聚类的方法存在时间复杂度过高的缺点,故而采用基于1.3节所提的改进LSH算法以贪婪机制实现快速划分。 设itemj={(i1,ri1,j),(i2,ri2,j),…,(im,rim,j)} 为m个用户对项目j进行的评分集合。因此,当项目数量为n时,集合数量为n。其次,为了对由类似用户评分的项目进行聚类,应用1.3节中所述的改进LSH函数,可将整体项目集合划分为数量为n′的子项目集合,满足n′≤n,且由1.3节可知,相似用户评分的项目有较高的概率属于同一组。 基于上述划分,在次轮的相似性计算过程中,可分别计算不同子项目集的内部相似度。与传统将项目集合考虑为整体的相似矩阵构造方法相比,所提划分方法显然减小了相似性计算轮次中的计算开销。 该轮次中,map函数将三元组 (i,itemj,ri,j) 转变为键值对itemj,(i,ri,j)。 在混洗阶段,由于发出的键值对所有映射函数按每个不同的密钥分组,具有相同秘钥的键值对(即项目itemj)被分至同一组。然后,用itemj和对应的键值对列表调用每个reduce函数(即1.3节所提改进LSH算法),最终按照用户编号i以升序方式对 (i,ri,j) 进行排序,并将项目itemj和键值对列表存储在名为LSH的HDFS文件中。最终,具有相同Hash值的用户-项目评分列表被存储在同一文件中。算法1示出了项目集划分的伪代码。 算法1: 项目集划分伪代码 Functionitem_set_partition.map(key, (i,itemj,ri,j)) 参数含义: Key: 键值对, 初始为空;i: 用户id; itemj: 项目id; ri,j: 对itemj的评分列表 Begin (1) emit (i,itemj,ri,j) End Functionitem_set_partition.reduce (itemj,LSH) 参数含义: itemj: 项目编号; LSH: 具有相同Hash值的用户-评分列表 Begin (1)InputSUM=0, LSH=∞,a=1, K=0 (2)For列表LSH中的每个(i,ri,j) doSUM=SUM+ri,j; (3)Fora=1∶1∶k do If(ha(ri,j) LSH=ha(ri,j) (4) Append (LSH, (itemj,sort(LSH))) End 本轮次的目的在于计算隶属于同一子项目集合中的内部相似度。由于在上一轮次中,将具有相同Hash值的用户项目集合存储在同一名称下的HDFS文件中,因此,通过扫描存储这些文件的目录,可以获得文件名列表。然后,使用Hadoop API显式地为每个映射器分配每个文件。 用于子项目集合内相似性计算的伪代码如算法2所示。每个map函数对应于处理由若干个 (i,ri,j) 组成的列表,即LSH。在列表LSH中,所有项目具有相同的Hash值。为了获得每个子项目集合内部的相似性,即Pearson相关性的统计数据,首先加载每个子项目集的列表LSH。在算法实现过程中,为有效查找项目itemi的统计信息,将计算得到的Pearson统计信息编制为一个新表,记为PEARSON_TABLE,从而便于第三轮次计算不同子项目集合间的相似度。 如前所述,经过LSH算法处理后的子项目集合以按照用户编号i以升序方式对 (i,ri,j) 进行排序,并将项目itemj和键值对列表存储在名为LSH的HDFS文件中。故而,对于每一个子项目集合而言,可采用线性扫描的方式根据式(3)计算子项目集合内部的相似度,随后将计算结果存储在HDFS文件中。 在计算完毕所有子项目集合的相似性后,将LSH中的用户-项目评分列表重新排列为下一轮次计算的项目-评分列表,而对于项目itemj的每个用户-项目评分对 (i,ri,j), 发出键值对 (i,(itemj,ri,j))。 而在混洗阶段,具有相同秘钥i的项目-评分对 (itemj,ri,j) 被分到同一组。因此,每个reduce函数简单地取得由单个用户i分级的所有项目评分对的列表。 算法2: 子项目集合内部相似度计算伪代码 Funtioninternal_sim_calculation.map(key,LSH) 参数含义: Key: 键值对, 初始为空 LSH: 具有相同Hash值的用户-评分列表 Begin (1)InputLSH(i,ri,j) (2) PEARSON_TABLE=get_statistics(PEARSON) (3)ForLSH列表中的每个 (itemj1,ri1,j1)和 (itemj2,ri2,j2) do SUM=0;pj1=0;pj2=0; (4)For每个(i1,ri1,j1)∈itemj1Do For每个(i2,ri2,j2)∈itemj2Do If(i1=i2)then (6) Append (S, (i1,i2,Sim(i1,i2))) (7)ForLSH中的每个(itemj,ri,j)Do Foritemj中的每个(i,ri,j)Do Emit (i, (itemj,ri,j)) OutputEmit (i,LSH) End Funtioninternal_sim_calculation.reduce (i,LSH) 参数含义: i: 用户id; LSH: 具有相同Hash值的用户-评分列表 Begin (1)Emit (i,LSH) End 该轮次MapReduce映射阶段,每个map函数通过使用隶属于不同子项目集合的评分rj和rj′来计算子项目集合间的相似度,记为Sim(j,j′);而在归约阶段,通过扩充Sim(j,j′)的结果来生成最终的相似矩阵。区别于传统串行算法以穷举的方式计算相似矩阵,本轮次使用隶属于不同子项目集合的评分列表{rj}和{rj′}来计算不同组件的相似性。 设用户i对应一组项目 {itemj1,itemj2,…,itemjt}, 相应的评分列表为Ri={ri,j1,ri,j2,…,ri,jt}, 而用户内部相似度已经在2.2节中计算给出,故而这一轮次计算中可仅使用第二轮次生成的项目-评分列表来并行计算不在同一组中的项目对的相似度。 算法3: 子项目集间相似度计算伪代码 Funtionexternal_sim.map.setup() Begin 1.LSH_table=get_LSH(LSH) 2.PEARSON_TABLE=get_statistics(PEARSON) End Funtionexternal_sim.map(i,Ri) 参数含义: i: 用户编号;Ri: 用户评分列表 Begin (1)InputRi={ri,j1,ri,j2,…,ri,jt} (2)For对于每个用户-评分对(i1,ri1,j1)和(i2,r2,j2)Do (3)If (LSH_table.lookup(itemi1)≠(LSH_table.lookup(itemi2)) then End Funtionexternal_sim.reduce (key, List) 参数含义: Begin (1)InputSUM=0,pi=0,pj=0 (3) Append (S,(i1,i2,Sim(i1,i2))) End 其具体伪代码如算法3所示。在调用所有映射函数之前,每个映射器的设置函数将用于计算相似性的所需统计信息,加载到PEARSON_TABLE中,并从HDFS文件PEARSON中,将每个LSH函数值分别加载到LSH中。 其次,调用map函数对不同用户i1、i2和用户的评分列表进性相似性计算。对于LSH中的每对项目-评分对(itemj1,ri1,j1)、(itemj2,ri2,j2),首先检查项目itemj1和itemj2是否属于同一组。若属于同一组,则已在前一轮次中已经计算得到它们的内部相似度;否则便根据式(3)计算它们的Pearson相似度,并生成键值对(itemj1,itemj2)。值得一提的是,由于在第一轮中利用LSH技术对类似用户评分的项目进行聚类,故项目间的Pearson相似度较小。 在混洗阶段,具有相同键值的键值对被划分为同一组。然后,每个reduce函数使用键值对(itemj1,itemj2)获取对应的用户-评分列表,进而依据式(3)进行子项目集合间的相似度计算,最终存储到HDFS文件中获得最终的相似矩阵。 为衡量所提算法的执行效率与可扩展性,选择文献[12]所提串行相似矩阵构造算法与文献[13]所提两轮次MapReduce构造算法作为对比,见表1。 表1 相似性矩阵构造算法 令所有算法在相同软、硬件环境下运行。计算节点数量选择为41个,包含一台主机负责任务分配与管理以及40台普通计算节点。主机配置为:3.5 GHz Intel Xeon E5-2697 v2 CPU, 32 GB内存以及1 T硬盘;其余计算节点配置为:3.2 GHz Intel Core i5-6500 CPU, 8 GB内存以及1 TB 硬盘。所有计算节点间通过转发带宽为1 Gbps的以太网交换机连接。所有计算节点均安装Linux操作系统(Ubuntu 10.04.4版本),底层使用Hadoop 2.0.0版本实现分布式文件管理。而所有算法则使用Javac 1.8版本进行编译。 基准实验中,采用常用的MovieLens公开数据集作为案例进行算法性能测试。该数据集用明尼苏达大学Group-Lens 研究项目所开发。采用的5分制评分原则对电影从各个角度进行评分。其包含ML(100 k)、ML(1 M)、ML(10 M)和ML(20 M)这4个子数据集。对比指标选择为不同算法在执行相同次数(设置为10次)的平均执行时间。算法的性能约束测试主要包括局部敏感哈希函数执行次数、数据集大小、计算节点数量、不同相似程度度量对执行效率的影响。 3.2.1 LSH函数执行次数对推荐算法执行效率的影响 首先讨论LSH执行次数对项目集合分组的影响。图3为当达到相同的相似性时,所提算法在数据集ML(20 M)上的执行时间。可以看出,随着LSH执行次数的增加,执行时间并不严格随着执行次数的增加而增加,当LSH算法执行次数从1增加到7时算法执行时间由20 163 s逐渐下降到4737 s,随后算法执行时间将逐渐增加。这是由于当LSH算法运行足够次数后,项目集合的相似度不再发生明显的变化,反而会引发额外的开销。 图3 推荐算法执行时间随LSH算法运行次数的变化关系 3.2.2 数据集大小对推荐算法执行效率的影响 本小节讨论数据集规模对采用表1中不同相似性矩阵构造方法的推荐算法执行效率的影响。令LSH函数的执行次数为7,图4示出了当数据集规模由ML(100 k)增加到ML(20 M)时,所有算法的执行时间均逐渐增加。由于传统串行方法对以枚举方式进行评分的相似度求解,因而此算法的运行时间最长,且随着数据集规模的扩大,其运行时长也急速增大。两轮次MapReduce方法由于缺少了LSH算法对项目进行分类,但由于采用了并行计算的方法,故而执行时间介于传统算法与所提算法之间。此外,由图4可以看出,所提算法与传统算法相比,其推荐算法运行时间比文献[12]和文献[13]所提算法在数据集规模较大时分别缩短了34.5%和14.4%。实验结果表明所提算法具有更高的执行效率,同时也表明所提算法对更大规模数据集场景时展现出了良好的可扩展性。 图4 推荐算法执行时间随数据集规模的变化关系 3.2.3 计算节点数量对推荐算法执行效率的影响 本小节讨论计算节点数量对推荐算法执行效率的影响,设LSH函数的执行次数仍为7,数据集仍使用ML(20 M)。如图5所示,由于传统串行算法不考虑分布式计算框架,因此算法运行时间保持不变;而对于后两者算法而言,当计算节点从11变化到51时,所有相似矩阵构造方法下的推荐算法执行时间均逐渐下降。然而,与其它相似矩阵构造方法相比,所提算法在所有的实验设置场景下均具有最小的执行时间,且比其它两种算法的执行时间分别节约26.4%和14.4%以上。上述实验结果表明,所提算法对新扩充的计算节点具有更优异的扩展性,能够使计算节点具有更短的计算时间,从而进一步验证明所提算法具有更快的执行效率。 图5 推荐算法执行时间随计算节点数量的变化关系 3.2.4 不同相似性度量方法对算法执行效率的影响 此外,由于相似性度量方法除Pearson相似性外,还有余弦相似性[14]和Jaccard相似性两种[15],分别如式(4)和式(5)所示。因此,本小节进一步考察采用所提相似矩阵构造算法时,不同相似性度量策略下对推荐算法执行效率的影响。设LSH函数执行次数为7,数据集选用ML(20 M) (4) (5) 图6示出了不同相似性度量方法下推荐算法的运行时间。可以看出,在相同实验条件下,Pearson相似性度量比余弦相似性度量和Jaccard相似性度量的运行时间分别高1196 s和926 s。其原因在于,从式(3)-式(5)可以看出,Pearson相似性度量需要获取用户编号和对应的项目评分两种统计信息,而余弦相似性度量和Jaccard相似性度量则仅需要其中的一种,因而计算效率上而言Pearson相似性度量慢于后两者,而后两者的计算效率则相差不大。 图6 不同相似性度量方法下推荐算法运行时间 针对海量数据下推荐算法性能提升瓶颈问题,提出了基于3轮次MapReduce计算的相似矩阵并行构造方法,包含3个主要部分:项目集合划分、子项目集内部相似性计算和子项目集间相似性计算。在首轮次项目集合划分时,提出了利用多次LSH算法进行项目集合快速划分的改进算法,从而提升了后续轮次计算时的运行效率。实验结果表明,与传统方法相比,所提算法具备良好的执行效率与可扩展性。未来工作将深入研究不同相似性度量方法下推荐系统的推荐性能提升策略。




1.4 Pearson相似性度量


2 相似矩阵并行构造方案
2.1 项目集划分
2.2 内部相似度计算


2.3 子项目集合间相似度计算


3 算例验证与结果讨论

3.1 软、硬件实验参数
3.2 实验结果





4 结束语
