砂卵石地层盾构隧道地表最大沉降量预测

韦 猛，方中杨，柴冰冰，亓金慧

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

0 引 言

Peck在分析了英国地铁施工中大量的沉降数据和相应工程资料后，于1969年提出在不排水情况下隧道开挖引起的沉降槽体积应等于地层损失体积，并指出地表沉降曲线符合正态分布曲线[1-3]。在预测地表最大沉降量Smax时，沉降槽宽度i和地层损失体积V受地质特征和施工条件的影响[4]。国内外学者[5-8]认为沉降槽宽度i与隧道直径关系很小，而与隧道埋深H、施工条件及地质特征有关；韩煊等[9]提出黏性土地面沉降槽宽度参数k=0.5；袁大军等[10]针对南京长江隧道工程，研究了超大直径泥水平衡盾构对土体扰动的沉降槽宽度的影响范围；刘建航等[11]总结了上海粉细砂土隧道沉降规律，提出了“欠地层损失”的概念。对于地层损失的确定，学者们多采用传统经验法。韩煊等[12]研究表明，在硬黏土中用敞开式盾构开挖，地层损失率为1%～2%；魏纲[13]研究得出，在砂土地层中闭胸开挖隧道，地层损失通常小于0.5%；朱才辉等[14]研究得出，土压式盾构隧道在软黏土地层中损失率为1%～2%。对于一些土质较好，施工技术、施工设备相对完善的工程，经验法具有一定参考价值和优越性，但是在施工条件、地层条件相对复杂时，经验法计算结果与实际值往往偏差较大，并且随着施工设备的改进、施工控制手段的逐渐加强，经验法的弊端也随之放大。所以周奇才等[15]用出渣量-注浆量-管片体积方法来确定地层损失。

笔者依据成都地铁17号线白机区间地表沉降实测数据和掘进数据，对沉降槽宽度i和单位地层损失V展开研究，得到隧道埋深H=10～19 m时i与H的关系；并对周奇才[15]的单位地层损失V计算式进行了修订，引入有效注浆率n2(n2=有效减缓地层损失的注浆量/全部注浆量)参数，提出了用已知盾构刀盘半径、管片外径、总注浆率、出渣量、注浆量、渣土松散系数、隧道埋深等现场数据计算地表最大沉降量的公式，并在成都地铁17号线机终区间进行了验证。

1 工程概况及地质特征

成都地铁17号线白佛桥站—机投桥站(白机区间)采用盾构法施工，起止里程YDK 75+702.956～YDK 76+877.598，最小曲线半径800 m，纵坡0～3.159～2.000～0(‰)，覆土厚度10～19 m。盾构主要穿越中密砂卵石土。区间场地为第四系地层覆盖，地表多为人工填土覆盖，其下为冲积砂土及卵石土。盾构穿越地层及特征描述见表1。区间穿越地层见图1。

表1 白佛桥站—机投桥站盾构穿越地层组成及特征描述

图1 白佛桥站—机投桥站盾构区间穿越的地层

2 Peck公式介绍

1969年Peck指出了隧道开挖引起地面沉降曲线符合正态分布曲线，并给出了求解最大沉降量的Peck公式：

(1)

(2)

(3)

式中：Sx为地表沉降量，mm；x为测点距隧道中线距离，m；Smax为地表最大沉降量，mm；V为单位长度地层损失体积，m3；i为沉降槽宽度，m；H为隧道埋深，m；φ为土体内摩擦角，(°)。

3 i的确定

笔者根据成都地铁17号线白机区间现场监测数据来分析砂卵石地层沉降槽宽度i与隧道埋深H的关系。

3.1 实测数据回归分析

对式(1)两边取对数，得

(4)

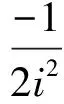
成都地铁17号线白机左线断面DBC-75795的实测沉降量Sx测见表2。

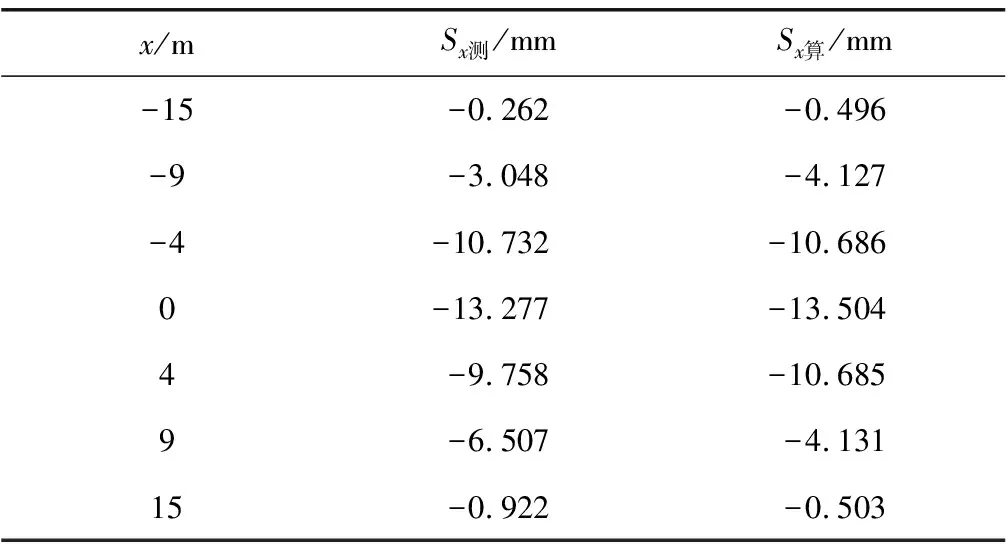
表2 断面DBC-75795实测沉降量

将表2的x、Sx测转化得到x2、lnSx算，再进行线性拟合得到回归方程(5)：

lnSx算=2.603-0.015x2

(5)

相关系数R2=0.914，表明回归线性关系显著。

结合式(4)、式(5)可得Smax算=-13.507 mm、i=5.844 m，即根据实测数据线性回归后的修订Peck式为

(6)

根据修订Peck式(6)计算得到各点地表沉降量Sx算，结果见表2。

图2为实测及回归计算得到的地表沉降量曲线。

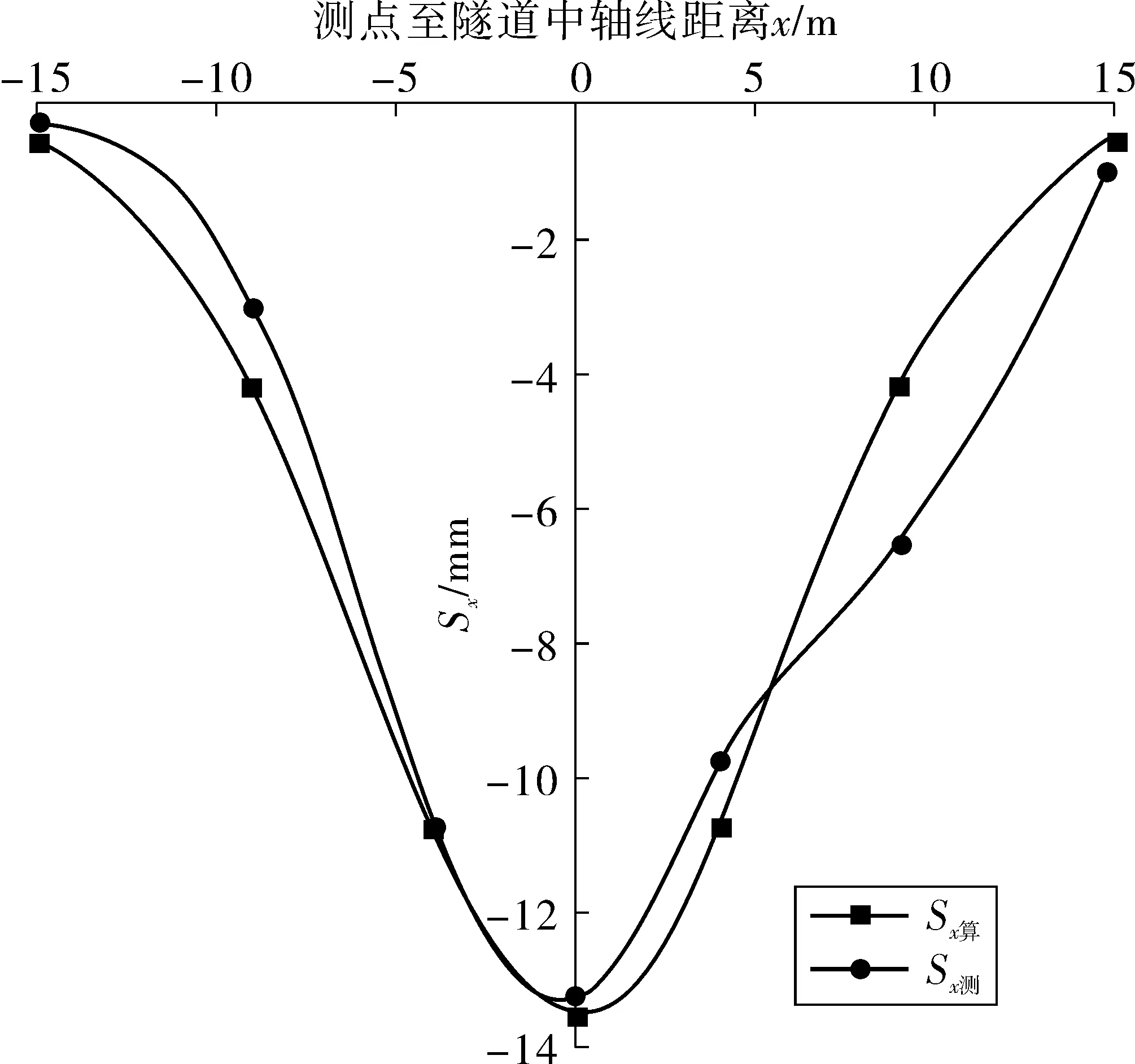
图2 地表沉降量回归计算值与实测值曲线

从图2可以看出，回归值曲线与实测值曲线最大沉降量差异不大，说明所选断面DBC-75795沉降实测数据较为合理，且二者变化趋势较为一致，表明用沉降量实测值线性回归后得到的修订Peck式(6)来求沉降槽宽度i是可行的。

3.2 沉降槽宽度i与隧道埋深H的关系

表3为根据白机区间隧道埋深H及其所对应的断面实测值回归后求得的i值。

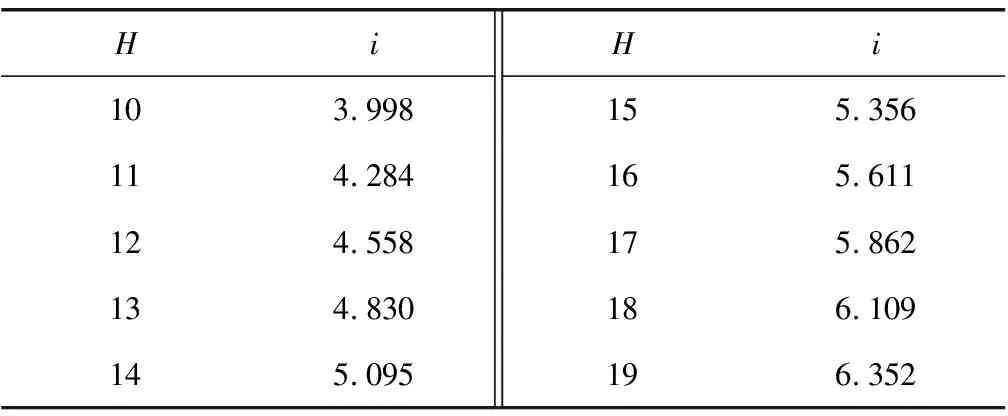
表3 白佛桥站—机投桥站隧道埋深H与沉降槽宽度i统计

对表3中数据进行拟合，发现i与H的关系符合Allometricl模型(7)：

i= 0.758H0.722

(7)

R2= 0.975

3.3 Allometricl模型适用性验证

成都地铁17号线机终区间(机头桥站—终点接收井)与白机区间(白佛桥站—机头桥站)相连。在机终区间左线选取5组典型断面实测沉降量，以对Allometricl模型(7)进行验证。各断面隧道埋深H=9、12、14、15、16 m，断面实测沉降量Sx测见表4。

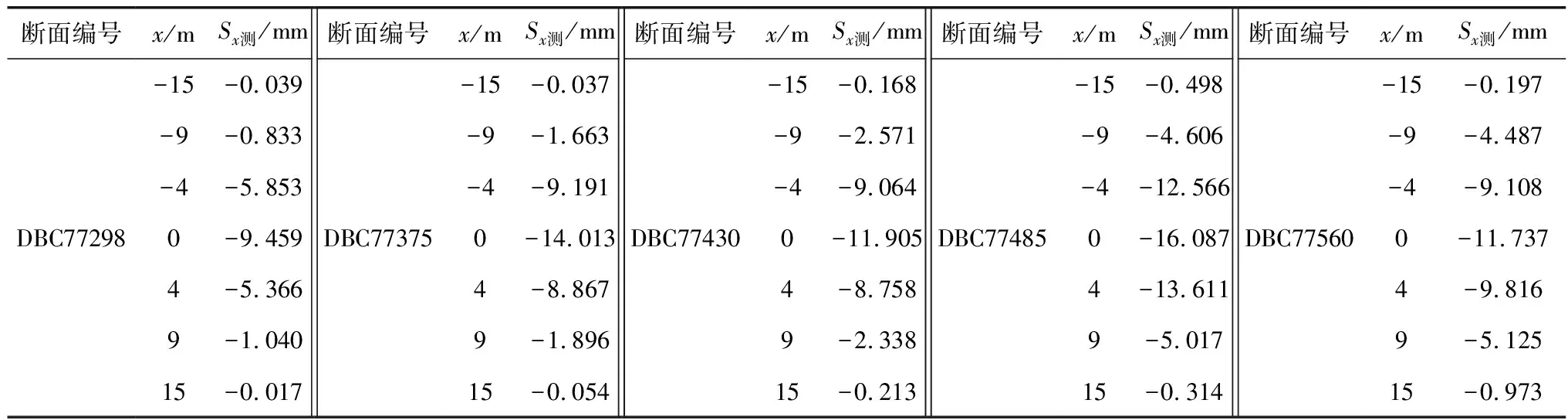
表4 机头桥站—终点接收井左线5组断面实测沉降量

对表4实测沉降量进行回归分析，得到各断面沉降量回归式 lnSx=a+bx2，再根据式(4)得到实测回归的沉降槽宽度i；将各断面对应的隧道埋深H代入式(7)，从而得到根据Allometricl模型(7)计算的沉降槽宽度i，结果见表5。

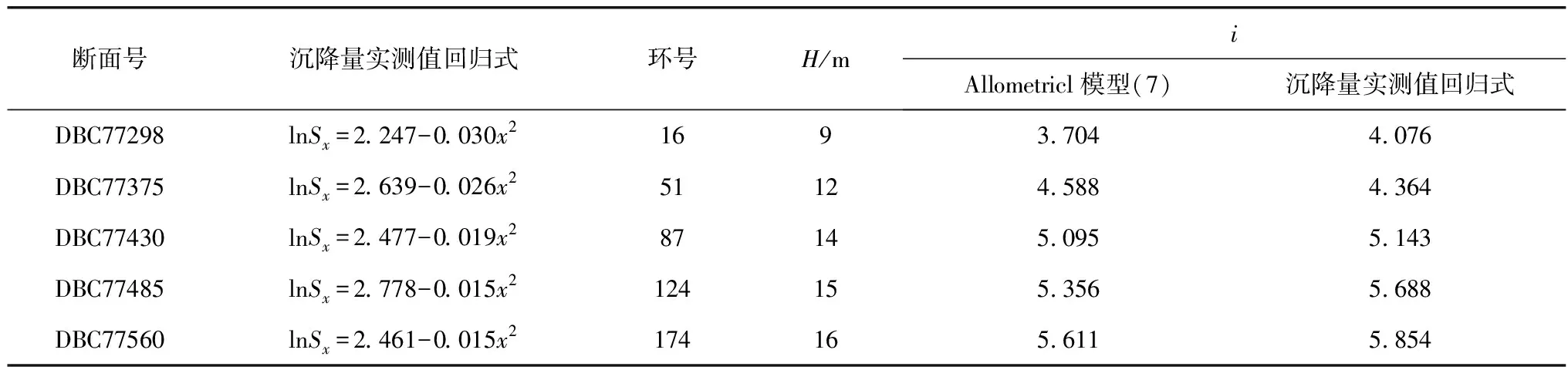
表5 实测沉降量线性回归公式及Allometricl模型公式计算得到的沉降槽宽度i值

从表5可以看出，Allometricl模型(7)求得i与实测值回归得到的i相差无几，说明可以用Allometricl模型(7)来表达砂卵石地层轴线埋深10～19 m隧道沉降槽宽度i与隧道埋深H的关系。

4 V求解分析

笔者根据掘进数据对周奇才等[15]用出渣量-注浆量-管片体积方法确定的地层损失进行验证，发现偏差很大；而从实际施工经验及监测信息可以看出，注浆量的微弱变化会导致地表沉降量发生超过6 mm的变化。因此，笔者结合白机区间盾构掘进数据，提出用有效注浆率n2这个参数来计算防止地层沉降的有效注浆量。

单位长度地层损失体积V按式(8)计算：

(8)

式中：V1为单环出土体积，m3；n1为渣土松散系数；V2为单环注浆体积，m3；n2为有效注浆率；n为单环总注浆率(总注浆量/间隙体积)；V3为单环管片外径所占体积，m3；L为单环掘进长度，m。

在掘进中，往往要加水、泥(膨润土)及泡沫等改良掌子面，并且开挖后，土体体积相对于开挖前有所增加。因此，在盾构完成100 m试掘进后，通过测试现场渣土来确定渣土松散系数n1的值。

向地层土体与管片之间的间隙注浆，浆液会进入周边地层，如图3。

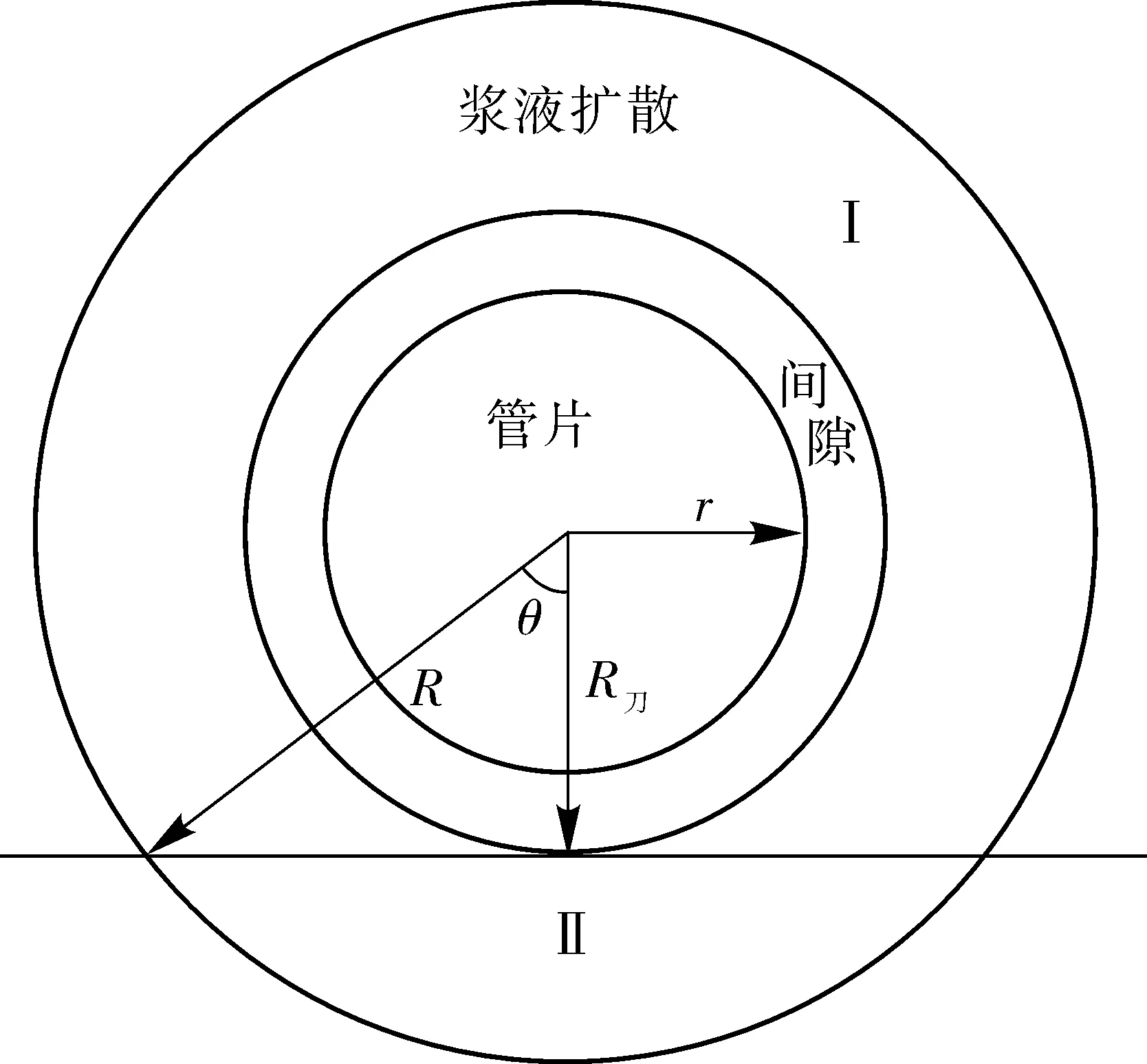
图3 管片壁后注浆示意

为了计算有效注浆率n2的理论值，需做如下假设：①管片没有上浮或下沉；②浆液在地层中均匀向圆周扩散；③浆液迅速在间隙中固结；④间隙浆液固结体和管片为统一刚体。

笔者认为图4中Ⅰ部分的浆液扩散量为有效浆液扩散量Q1，则有效浆液扩散量在总浆液扩散量Q中的占比ω可按式(9)计算：

(9)

(10)

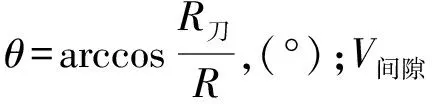
从而，有效注浆率n2为

(11)

根据盾构机和管片型号，利用盾构实测的单环出土体积V1和单环注浆体积V2，按式(12)来预测地表最大沉降量Smax：

(12)

5 地表最大沉降量Smax验证

选择机终左线盾构掘进状态良好的第174环(断面DBC77560)掘进数据来验证最大沉降量计算式(12)。R刀=8 634 mm，r= 8 300 mm，V1=116.0 m3，V2=8.2 m3，H=16.0 m，n=1.8，L=1.5 m,n1=1.3。

分别采用笔者提出的最大沉降量计算式(12)及周奇才等[15]未考虑有效注浆层面的计算式来计算最大沉降量Smax算，并算出最大沉降量计算值与实测值Smax测误差的绝对值|Δ|，结果见表6。

表6 计算结果汇总

从表6可以看出，用笔者提出的式(12)计算得到的最大沉降量值与实测值误差仅为1.355 mm，远远小于周奇才等[15]不考虑有效注浆率时的计算结果(16.020 mm)，证明笔者提出的采用沉降槽宽度i和单位地层损失V两个参数来确定最大沉降量更合理。

6 结 论

1)用实测沉降量做回归分析后得到的修订Peck式来求地表沉降槽宽度i是可行的。

2)地表沉降量实测值线性回归后得到的沉降槽宽度i与对应的隧道埋深H符合Allometricl模型关系，该模型关系可以用于埋深10～19 m砂卵石地层盾构隧道沉降槽宽度的求解。

3)为了提高单位地层损失V的求解精度，提出了有效注浆率n2参数，并给出了计算方法。

4)推导了砂卵石地层最大沉降量的计算公式，通过已知盾构刀盘半径、管片外径、总注浆率、出渣量、注浆量、渣土松散系数、隧道埋深等现场数据，可较为精准地得到地表最大沉降量。