基于滚动时域分解策略的原油混输调度模型

周智菊， 周 祥， 周 涵

(中国石化 石油化工科学研究院，北京 100083)

石油是不可再生资源，储量有限，据预测现今石油资源量只能维持人类未来50年的需求[1]。统计数据表明，2018年世界石油消费量已高达9.9843×107桶/d，较上一年增加了1.46%，其中仅中国石油的消费量就达到了1.3525×107桶/d，较上一年增加了5.33%[1]。面对巨大需求和有限资源之间的矛盾，世界各国，尤其是对外依存度近70%的中国，需要充分挖掘高硫、高酸类低成本劣质原油的价值[2]。

原油混输调度(又名“原油储运”)为炼油企业安排未来一段时间内的原油卸载、储存、运输、混合和蒸馏加工过程的操作任务，是石油加工过程的第一个环节[3]。优化的原油混输调度方案能够减少石油加工装置的进料切换，保证装置平稳运行，避免油轮滞期，降低成本，可在满足装置进料限值的前提下，使其尽可能多地加工劣质原油，为企业带来良好的经济效益[4]。因此，原油混输调度对石油资源的合理利用具有举足轻重的作用，其方案的优化研究受到广大学者[5-10]的关注。

学者们采用数学规划法[11-13]、约束规划法[14-15]、启发式算法[16-17]或元启发式算法[10,18]搭建原油调度数学模型，希望借助计算机手段实现原油调度方案的自动编制。其中，人们对数学规划方法的研究时间最长，该方法具有严格的优化评估机制，是最常用的原油调度模型化方法。然而，原油调度数学规划模型属于混合整数非线性规划(MINLP)模型，该模型具有非确定多项式可解的特征[19]，难以用于处理复杂原油储运的优化。为了提升模型的求解效率，部分学者提出采用连续时间表示方法[3,6,20-21]取代离散时间表示方法[22-24]建立原油混输调度模型。针对相同的调度问题，连续时间模型需要更少的时间段数，具有规模较小的特点，有利于提升模型的求解效率，但是该类模型包含大量Big-M 约束，模型整型度较高，这又会降低模型的计算性能[25]。因此，目前很难只通过合适的时间表示方法快速解决复杂原油储运问题[26]。

滚动时域分解策略原理简单、实施难度低，已经被应用到原油储运调度方案的优化过程中[27-29]。采用滚动时域分解策略，将较长调度周期划分成多个短周期，可以提高模型的求解效率，解决单一原油储运模型求解难的问题。但是，由于人为打破了一个完整体系间的相互联系，不能保证采用的分解算法一定能够获取优化、可行的问题解决方案。为了弥补这一缺陷，笔者提出“安全时间片段”的概念，将整个调度周期分解成多个时间块，每个时间块由一个“滚动时域片段”和一个“安全时间片段”所组成，在每次迭代测算时都能考虑到未来更长一段时间内的调度方案，从而降低了方案不可行的概率；同时，分析模型方案不可行的原因，在模型中添加必要的约束限制，改变搜索路径，进一步保证了模型的可行性和优化性。

1 原油混输调度存在的问题

图1为中国某沿海炼油企业的原油储运流程，其过程可以描述为：油轮(VLs)到港后停靠在空闲泊位(BE)，并将原油卸载至合适的码头罐(STs)；码头罐内一部分原油直接经过长输管线(PL)运输至厂区罐(CTs)，而另一部分原油则先经过转油线(ZL)输送至中转罐区(ITs)，然后再经过PL输送至CTs；最后CTs中原油被送至蒸馏塔(CDUs)进行加工处理。该储运流程具有2个特点：(1)连接码头和厂区的PL长度较长，无法忽略原油从PL的入线端移动至出线端的时间。这导致模型拥有很多的二元变量，严重影响模型的计算速率[30]。(2)该流程较为复杂，在文献[31]基础上增设了LTs和ZL储运资源，加大了模型的开发和求解难度。

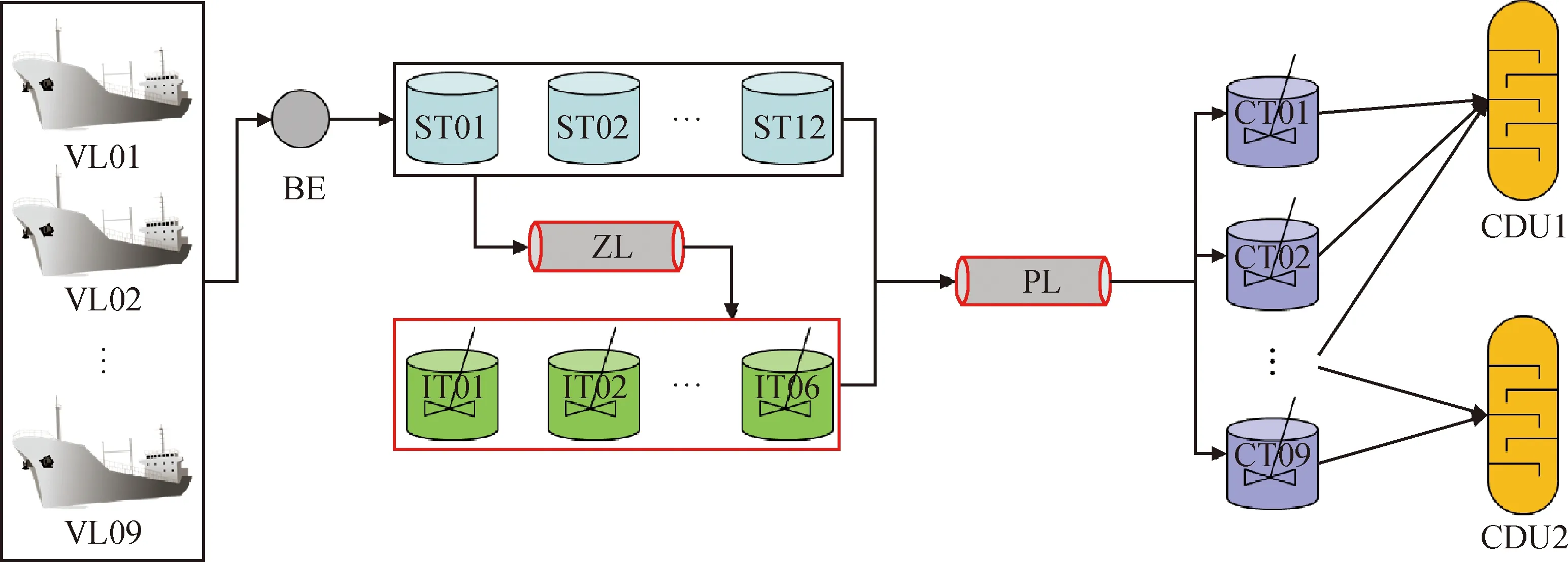
VL—Vessel； BE—Berth； ST—Storage tank； IT—Intermediate tank； CT—Charging tank；ZL—Zhuan pipeline； PL—Long-distance pipeline； CDU—Crude oil distillation图1 中国某沿海炼油企业的原油储运流程Fig.1 Crude oil scheduling process of an east coast refinery in China

了解了业务流程以后，为处理原油混输调度问题，建模者还需要收集如下信息：调度周期长度、油轮预计到港信息、炼油厂的结构细节、各储罐的库存信息和收油静置信息、油轮卸油速率范围、管线输送速率范围、常压塔生产需求，以及油种性质和组成配比等。其中，混炼原油组成配比和油轮载油参数见表1、表2；码头罐和厂区罐的收油静置时间分别为9 h和24 h，陆域罐收油后无需静置；其他参数参见文献[32]的表3～表5。

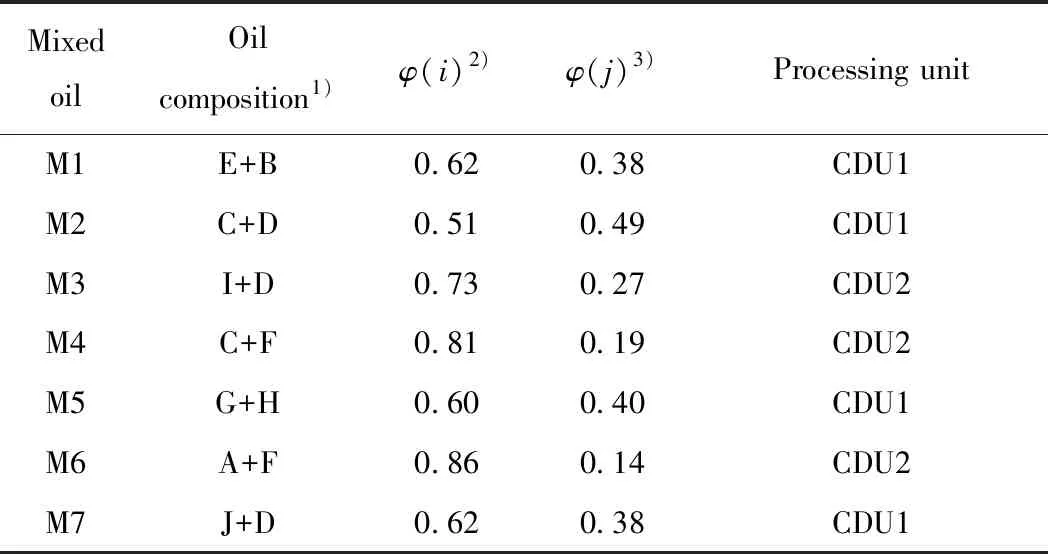
表1 混炼原油组成信息Table 1 Schemes for crude oil blending

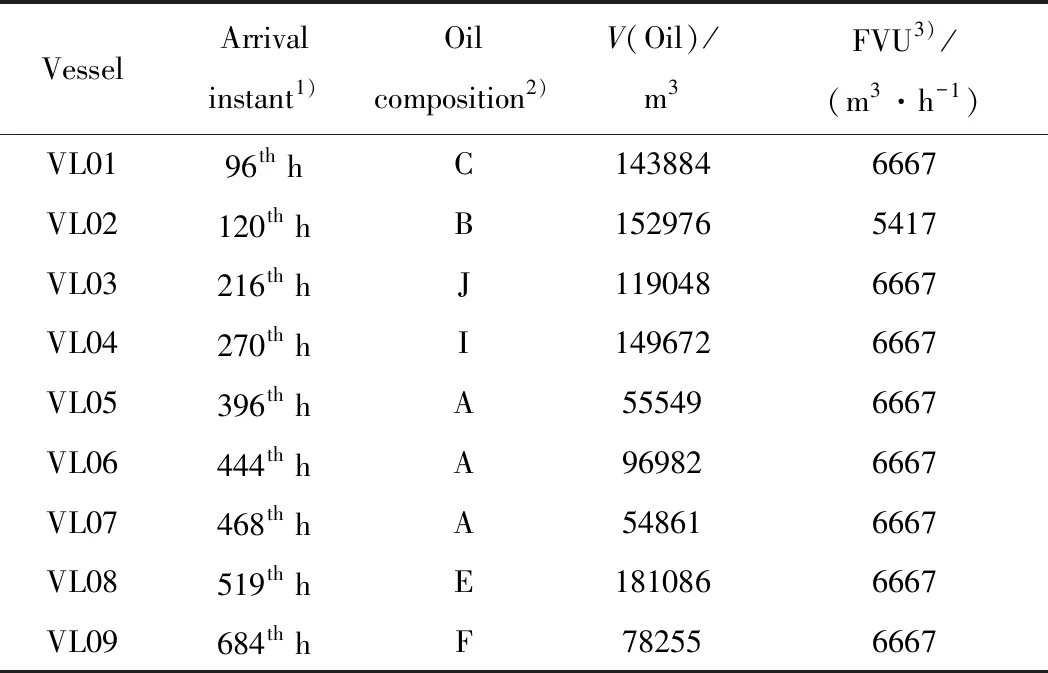
表2 油轮载油情况Table 2 Vessel estimated arrival time and crude oil loading

2 数学模型

针对图1原油储运过程建立连续时间MILP模型。该模型包括时间约束、油轮卸油约束、储罐(码头罐、中转罐、厂区罐)收付油约束、管线(转油线、长输管线)原油输送约束和常压塔进料约束。下面对模型特有的约束条件和目标函数进行描述，其他约束(如油轮离港时间)请参考文献[6]和文献[22]。

2.1 储罐状态约束

模型约束由参数、变量和关系表达式组成。变量又分为二元变量和连续变量。虽然该调度过程涉及码头罐、中转罐、厂区罐3种位于不同位置的储罐，但是，设置储罐状态约束的总体原则仍然是储罐不能同时发生收油和付油操作。该模型约束如式(1)～(3)所示。

∑b∈S2X(b,i,s)+∑z∈S7X(i,z,s)+
∑p∈S8X(i,p,s)≤1 ∀i∈S3,s∈S1

(1)

∑z∈S7X(z,k,s)+∑p∈S8X(k,p,s)≤1
∀k∈S4,s∈S1

(2)

∑p∈S8X(p,j,s)+∑d∈S6X(j,d,s)≤1
∀j∈S5,s∈S1

(3)

式(1)～(3)中：集合S1、S2、S3、S4、S5、S6、S7、S8分别表示时间段、泊位、码头罐、中转罐、厂区罐、常压塔、转油线和长输管线集合；字母b、d、i、j、k、p、s、z分别表示泊位、常压塔、码头罐、厂区罐、中转罐、长输管线、时间段和转油线的编码；变量表达式X(b,i,s)、X(i,p,s)、X(i,z,s)、X(j,d,s)、X(k,p,s)、X(p,j,s)和X(z,k,s)表示同一类二元变量，可以统一表示成X(u,u′,s)，其中u,u′表示除时间段编码s以外的编码全集。当X(u,u′,s)=1时，表示编码u所对应的设备在第s个时间段内向编码u′所对应的设备付油；当X(u,u′,s)=0时，表示编码u所对应的设备在第s个时间段内并未向设备u′所对应的设备付油。

2.2 性质约束

目前，很多研究[33-35]均是根据混合原油的某种性质指标来动态确定各单一原油的调合比例，但是这样处理会引入xy形式的双线性约束，使模型成为MINLP模型。对于这类模型，即使利用先进的商业求解器(CPLEX、XPRESS等)也无法在有限时间内获得全局最优或者次优解[36]。为了解决这一问题，学者们纷纷将MINLP模型转化，如分解成MILP和非线性规划(Nonlinear programming，NLP)两阶段模型[13,34,37-38]。这种方法可能会改善模型的计算性能，但是其优化出的原油调合方案将是任何混合比例的实数组合，企业难以操作。因此，本研究以已知混炼原油信息(见表1)为基础，固定混合原油调合比例，形成约束如式(4)和(5)，搭建纯MILP模型。这样既能保持模型的计算性能，又能提升方案的可操作性。

IC(u,c,s)=IM(u,m,s)×f(m,c)
∀u∈S3∪S4∪S5,c∈S9,m∈S10,s∈S1

(4)

∑m∈S10IM(u,m,s)=∑c∈S9IC(u,c,s)
∀u∈S3∪S4∪S5,s∈S1

(5)

式(4)和(5)中:集合S9、S10分别表示单一原油和混合原油集合;字母c、m、u分别表示单一原油、混合原油和储罐的编码;变量IC(u,c,s)和IM(u,m,s)分别表示储罐u内单一原油c和混合原油m在第s个时间段结束时的库存量，m3;参数f(m,c)表示单一原油c在混合原油m中的体积分数。

2.3 转油线输油操作约束

该调度流程转油线长度为11 km、输油管容量(简称管容)为3000 m3。为了降低模型复杂性，假定原油能瞬间从转油线入线端移动到出线端，即形成式(6)所示的物料平衡关系，其中，变量VC(i,z,c,s)和VC(z,k,c,s)属于同一类连续变量，分别表示在第s个时间段内码头罐i向转油线z、转油线z向中转罐k外付单一原油c的体积，m3。

∑i∈S3VC(i,z,c,s)=∑k∈S4VC(z,k,c,s)
∀z∈S7,c∈S9,s∈S1

(6)

2.4 长输管线顶油操作约束

该调度流程长输管线长度为163 km、管容为46000 m3。与转油线不同，无法忽略原油长输管线入线端和出线端的时间差。考虑到管线的输油操作相当于平推流过程，即先输送至管线的原油一定首先被顶出管线(见图2)，模型设置顶油操作约束如式(7)～(13)来模拟长输管线的实际运输过程。

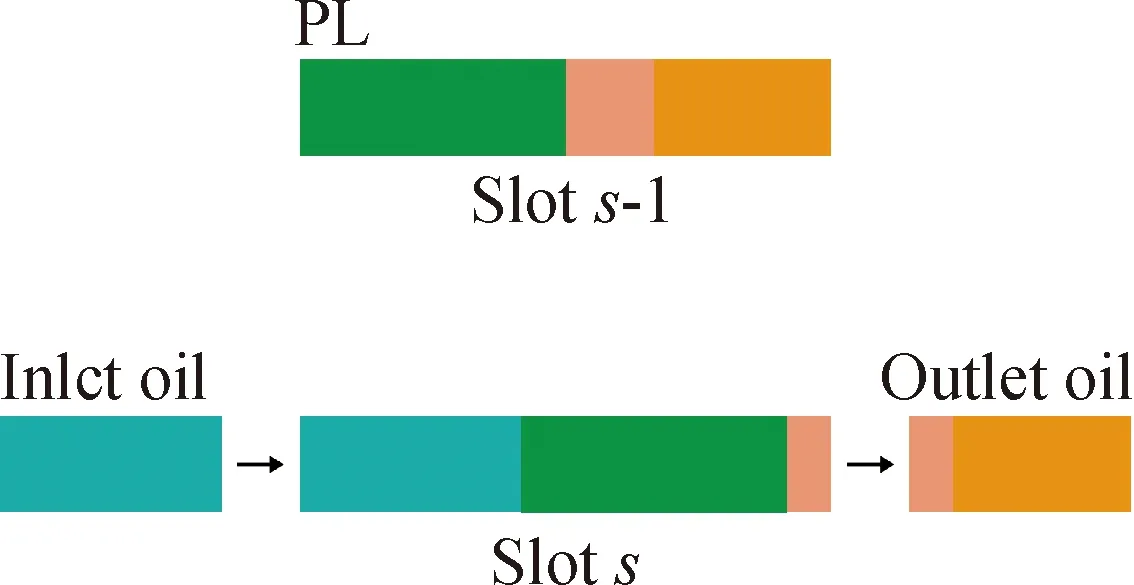
图2 长输管线原油输送示意图Fig.2 Schematic diagram of crude oil transportation in long-distance pipelines (PL)

B(l,s)≤∑ss≤sB(l-1,ss) ∀l∈S11,l>1

(7)

B(l,s)≥Y(l,l′,s) ∀l，l′∈S11,l′≤l,s∈S1

(8)

B(l,s)≤∑l′∈S1,l′≤lY(l,l′,s) ∀l∈S11,s∈S1

(9)

B(l,s)≥Z(l,l′,s) ∀l,l′∈S11,l′≤l,s∈S1

(10)

B(l，s)≤∑l′∈S11,l′≤lZ(l,l′,s) ∀l∈S11,s∈S1

(11)

Z(l,l′,s)=B(l,s) ∀l∈S11,s∈S1

(12)

Y(l,l′,s)≤1-Z(l,l′-1,s)
∀l,l′∈S11,l≤l′,s∈S1

(13)

式(7)～(13)中：S11表示原油输送过程中新生成的管线段集合；l和l′表示管线内原油段编码；而B(l,s)、Y(l,l′,s)和Z(l,l′,s)均为二元变量，其中B(l,s)=1表示管线段l在第s个时间段内进入管线p，Y(l,l′,s)=1表示在第s个时间段内由于管线段l进入管线p导致管线段l′被顶出，Z(l,l′,s)=1表示在第s个时间段内管线段l进入管线p，但管线段l′仍然保留在管线中。

2.5 目标函数

油轮滞期将引发高昂费用，起泵操作将导致长输管线输送速率和混油性质波动，蒸馏塔低负荷生产将会降低企业生产利润。因此，以最早油轮离港时间、最长长输管线输送时间，以及最大蒸馏塔加工量作为模型优化目标。

objective=max(-φ1TE(v)+
φ2TL(p,s)+φ3VT(u,s))

(14)

式(14)中：TE(v) 表示油轮离港时刻(设调度方案起始时刻为0，油轮离港时刻即为从起始时刻计时，油轮离开泊位的时刻)；TL(p,s)表示长输管线p在第s个时间段内的输油时长，h；VT(u,s)表示蒸馏塔u在第s个时间段内的加工量，m3；参数φ1、φ2、φ3分别表示油轮离港时间点、长输管线的输送时间、蒸馏塔的加工量的优化权重。

3 滚动时域求解策略

原油储运调度模型大致遵从每个设备在同一时间段内只进行一个操作原则，因此调度周期越短、设备操作切换越少，模型中时间段数越少，进而模型规模越小，越易求解。这体现了滚动时域求解策略的基本原则。该求解策略的主要实现过程为：将长调度周期划分成多个连续相邻的短周期，建立多个调度子模型；将前一个子模型的测算结果作为后一个子模型的初始参数，依次求解每个子模型，从而形成完整的储运优化方案。由于前子模型的测算结果即为后子模型的输入参数，大大缩小了后子模型求解的搜索空间，因此若不考虑前子模型对后子模型的影响，只简单分割调度周期，则后子模型可能会不可行，导致整体模型求解失败。为了避免发生这种情况，笔者在调度周期简单分割的基础上，提出了设置“安全时间片段”或“滚动时域安全约束”2种改进措施。

原滚动时域分解策略的常规处理方式为：按一定规律(如油轮到港时间、调度周期均匀分割等)，将整个调度周期划分成n个子调度周期，即“滚动时域片段”(Δt(n))。在此基础上，笔者为相邻2个子调度周期增设了重叠的“安全时间片段”Δt′(n)，Δt′(n)的取值在综合考虑油轮最快卸油时间和储罐收油静置时间的基础上，结合模型的计算效率来确定。由此，每一个复合子调度周期均由Δt(n)和Δt′(n)组成，但每次测算时只保留Δt(n)范围内的储运方案。以为期240 h的调度问题为例，假设Δt(n)=24 h，Δt′(n)=48 h，则第1个复合子模型需要测算从开始时刻到第72 h的调度方案，但仅保留前24 h的方案，后48 h的方案被用于保证后复合子模型的可行性和优化性；随后，时间轴往后滚动24 h，进行第2个复合子模型的测算，以此类推，直至优化出240 h的执行方案。

储罐的收油静置时间达到24 h即可满足生产需求。油轮的最大载油量为181086 m3(见表2)，可在28.24 h后卸空，而Δt′(n)=48 h，Δt′(n)大于卸油时间28.24 h和静止时间24 h，因此“安全时间片段”足够长，能够保证储罐付油方案满足静置要求和获取优化的油轮卸油方案。但是，长输管线内原油输入输出不同步，码头罐和中转罐中原油只有符合一定配比关系(见表1)才能形成混炼原油进入长输线，长输线内原油只有满足某厂区罐内原油性质要求才能被输出至该厂区罐，因而模型无法保证在Δt(n)+Δt′(n)时间点后长输线的输送情况。因此可能出现2种情况：(1)码头罐和中转罐的期末库存不能调合成足够数量的混炼原油，导致长输管线长时间停输；(2)管线内存油的油种不合适，导致某些蒸馏塔进料过于充足，但其他装置进料不足，从而影响到模型的优化性，甚至可行性。为此，创造性提出了“滚动时域安全约束”如式(15)～(22)。

其中，厂区罐收油后需要静置一段时间(T1，h)才能往外付油，因此，为了保证蒸馏塔连续加工，要求厂区罐的期末库存量必须满足蒸馏装置T1时间内的加工需求量，如式(15)和(16)。

∑j∈S5ID(j,d)≥T1×FU(d) ∀d∈S6

(15)

∑d∈S6∑j∈S5ID(j,d)≥T1×∑d∈S6FU(d)

(16)

式中：参数FU(d)表示蒸馏装置d的最大加工速率，m3/h；连续变量ID(j,d)表示厂区罐j中可用于蒸馏装置d加工的期末库存，m3。

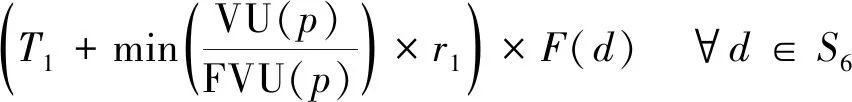
(17)

∑d∈S6ID(p,d)=VU(p) ∀p∈S8

(18)

式(17)和(18)中：参数VU(p) 表示长输管线p的管线容积，m3；FVU(p) 表示长输管线p的最大输送速率，m3/h；连续变量ID(p,d)表示长输管线p内可用于蒸馏塔d加工的期末管存油量，m3。比例参数r1表示原油通过长输管线时间对厂区罐期末库存和长输管线管存油总量的影响。r1的理论值为1，但是若设置r1=1，受原油库存、油轮载油情况等因素的影响，通过执行模型优化方案可能出现长输线在Δt(n)+Δt′(n)周期内长期停输的现象。这与增设“滚动时域安全约束”以此提升模型可行性和优化性的目的相违背，因此设定r1=0.8。

机械制造与自动化专业（以下简称机制专业）是一个传统的工科专业，包括高职高专在内的各工科院校一般都开设有此专业。现阶段，省内外高职院校在知识必须够用的原则下对机制专业进行了一些积极的改革，培养目标更精准，培养模式更实用，课程体系更科学，积累了宝贵的经验。

只有码头罐和中转罐的期末库存能够形成足够数量的混炼原油(简称潜在混炼原油)，才能保证长输管线持续不间断输送，如式(19)所示。其中：比例参数r2表示码头罐和中转罐的潜在混炼原油总量相当于长输管线容积的最小倍数。当参数r2≥1时，一方面，模型可能会增加码头罐和中转罐的期末库存，这将延迟后续油轮的卸油开始时间；另一方面，可能会减少调度初期长输管线的输送量，这将影响到整个模型的优化性能，因此笔者也假定r2=0.8。码头罐只能储存单一原油，而中转罐可储存单一原油和混炼原油，因此码头罐和中转罐中可调合出混炼原油的期末库存量应该满足式(20)～(22)的要求。

∑m∈S10RIM(m)+∑m∈S10RKM(m)≥
r2×∑p∈S8VU(p)

(19)

∑m∈S10f(m,c)×RIM(m)≤∑i∈S3IC(i,c,NS)
∀c∈S9

(20)

∑m∈S10f(m,c)×RKM(m)≤∑k∈S4IC(k,c,NS)+
∑k∈S4f(m,c)×IM(k,m,NS) ∀c∈S9

(21)

RKM(m)≥∑k∈S4IM(k,m,NS) ∀m∈S10

(22)

式(19)～(22)中：RIM(m)和RKM(m)分别为码头罐和中转罐中潜在混炼原油m的体积量，m3；NS为时间段数。

4 计算与讨论

4.1 计算性能分析

分别采用完整单一模型(简称Single模型)、带有“安全时间片段”和“安全约束”的滚动时域模型(简称Rolling_S_C模型)、带有“安全时间片段”但不带“安全约束”的滚动时域模型(简称Rolling_S模型)、不带“安全时间片段”但带有“安全约束”的滚动时域模型(简称Rolling_C模型)，以及不带“安全时间片段”和“安全约束”的滚动时域模型(简称Rolling模型)为本调度过程编制出未来240 h和720 h的调度方案。

滚动时域模型测算调度方案的CPU累计耗时结果如图3所示。由图3可以看出：Single模型在运行7112 s后获取到240 h内的较优调度方案(NS=8，最佳目标函数值与最佳边界值间差距(GAP)=2%)，但在耗时72000 s后仍无法获取到720 h内的可行方案(NS=16)；Rolling_C 和Rolling模型分别在测算第240 h和264 h方案时出现了模型不可行的情况，Rolling_S_C和Rolling_S分别在159.9 s、270.16 s和806.64 s、903.81 s后成功编制出未来240 h和720 h的储运方案。

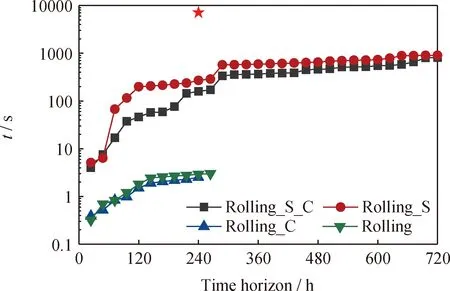
图3 滚动时域优化模型计算性能Fig.3 Calculation performance of rolling-horizon optimization models—Calculation time of the Single model for 240 h crude scheduling scheme

上述测试结果表明：

(1)Single模型确实很难快速解决长周期大规模问题。

(2)Rolling模型将调度周期简单划分成多个子调度周期(“滚动时域片段”)，缺乏约束限制，无法保证后子模型的可行性。滚动时域 Rolling_C 模型比Rolling模型更早出现了不可行的情况。这可能是因为：在2个模型中，前子模型对后子模型求解过程的影响程度不同；而且 Rolling_C 模型没有包含油轮的卸油问题，其模型不可行可能由油轮卸油不及时导致。

(4)虽然 Rolling_S_C 在 Rolling_S 模型基础上增加了“滚动时域安全约束”，模型更加复杂，但是 Rolling_S_C 的求解性能反而优于 Rolling_S 模型。原因在于：增加了“滚动时域安全约束”后，进行前子模型运算时考虑了后子周期的装置加工方案，因而保证了后子模型的可行性，降低了子模型可行域缩小的程度，因此能够更快搜索到模型的可行解。

特别说明，由于评估模型性能的首要标准是模型的可行性，其次才是其优化性能和计算性能，所以笔者并未对 Rolling_S 和Rolling、Rolling_S 和 Rolling_C、Rolling_S_C 和Rolling、Rolling_S_C 和 Rolling_C 的计算效率进行对比。

综上所述，带有“安全时间片段”的滚动时域模型可以在较短时间内处理大规模、长周期(720 h)的问题。

4.2 模型方案的优化性分析

由于Rolling和 Rolling_C 模型在计算过程中出现了不可行的情况，而且Single模型只获取了240 h优化方案，因此仅比较Single、Rolling_S 和 Rolling_S_C 模型未来240 h储运方案的优化性。

图4～图6分别为Single、Rolling_S 和 Rolling_S_C 模型测算方案的甘特图。由图4～图6 可知，3套方案均实现：(1)停靠在相同泊位的不同油轮按照到港顺序依次卸油；(2)所有储罐并未出现同时收付油操作的现象；(3)收油码头罐和厂区罐均静置了足够长时间(9 h和24 h)后才向外付油；(4)长输管线内原油满足先进先出的原则；(5)蒸馏装置全周期无间断加工；(6)油轮卸油速率、储罐收付油速率、蒸馏装置加工速率均符合速率上下限要求。因此，这3个模型所编制的方案均属于可执行方案。

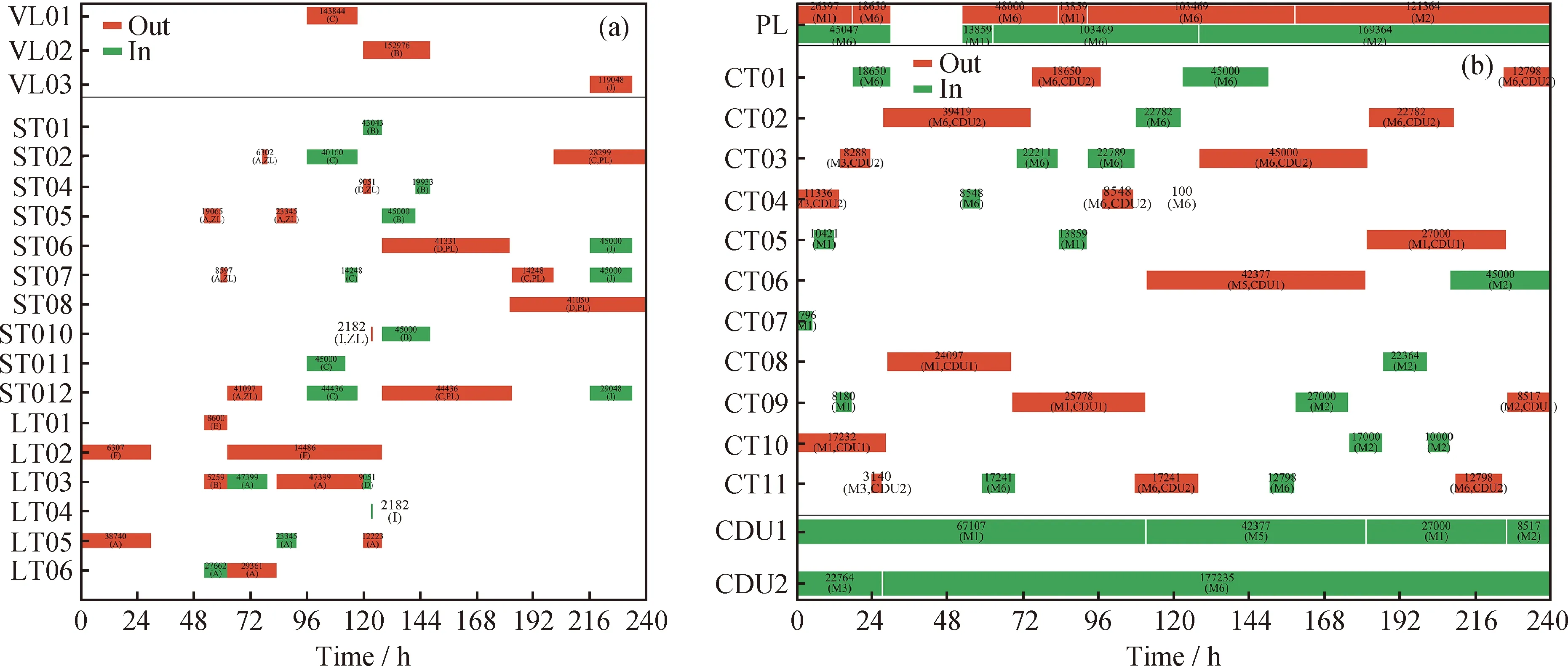
VL—Vessel； BE—Berth； ST—Storage tank； IT—Intermediate tank； CT—Charging tank；ZL—Zhuan pipeline； PL—Long-distance pipeline； CDU—Crude oil distillationA—Kuwait oil; B—DAR blend oil; C—Arabian light oil; D—Dalia oil; E—Nemba oil;F—Castilla oil; G—Oman oil; H—Plutonio oil; I—Basrah light oil; J—ESPO oilM1—Mixed crude oil blended by E (φ(i)=0.62) and B (φ(j)=0.38); M2—Mixed crude oil blended by C (φ(i)=0.51) and D (φ(j)=0.49);M3—Mixed crude oil blended by I (φ(i)=0.73) and D (φ(j)=0.27); M5—Mixed crude oil blended by G(φ(i)=0.60) and H (φ(j)=0.40);M6—Mixed crude oil blended by A (φ(i)=0.86) and F (φ(j)=0.14)图4 Single模型优化方案Fig.4 Optimization scheme proposed by the Single model(a) Optimization operations of vessels, storage tanks and intermediate tanks;(b) Optimization operations of a long-distance pipeline, charging tanks and distillation units

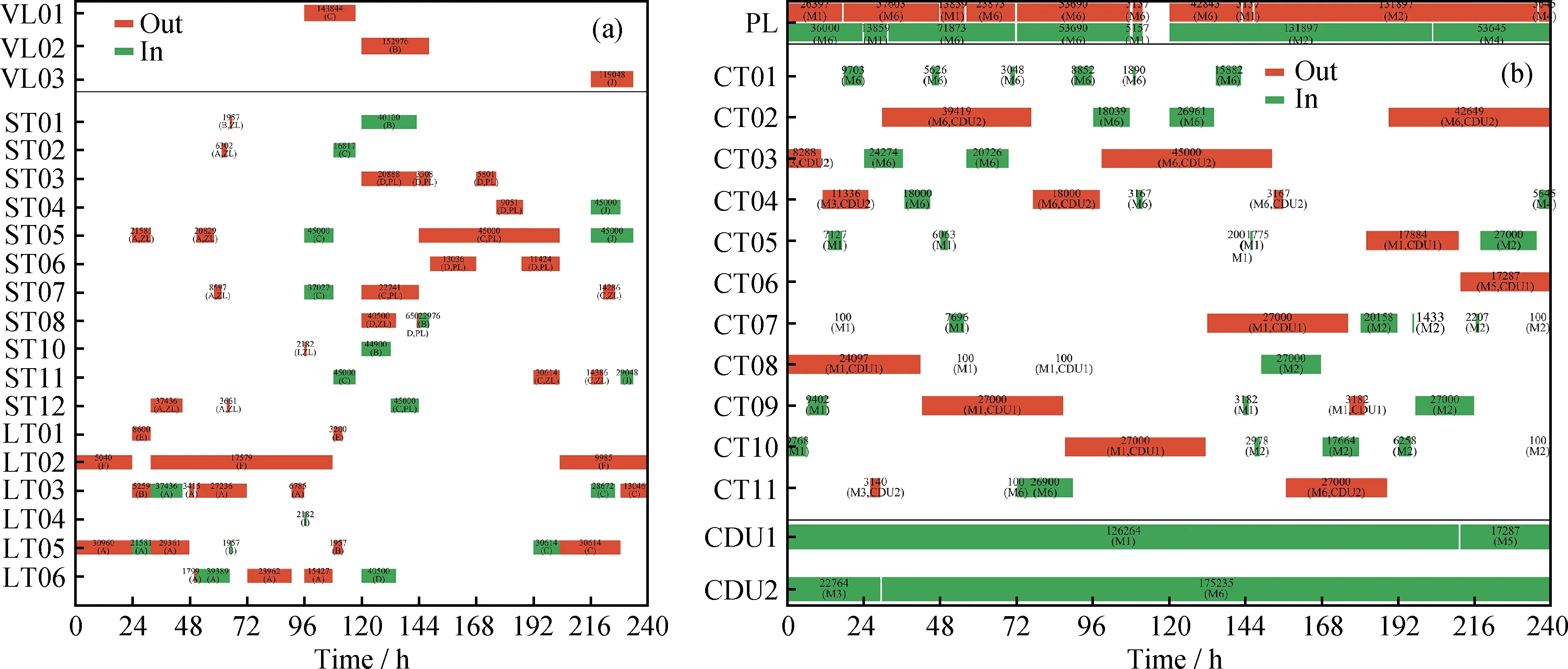
VL—Vessel； BE—Berth； ST—Storage tank； IT—Intermediate tank； CT—Charging tank；ZL—Zhuan pipeline； PL—Long-distance pipeline； CDU—Crude oil distillationA—Kuwait oil; B—DAR blend oil; C—Arabian light oil; D—Dalia oil; E—Nemba oil; F—Castilla oil; G—Oman oil;H—Plutonio oil; I—Basrah light oil; J—ESPO oil

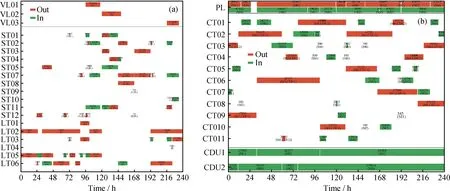
VL—Vessel； BE—Berth； ST—Storage tank； IT—Intermediate tank； CT—Charging tank；ZL—Zhuan pipeline； PL—Long-distance pipeline; CDU—Crude oil distillationA—Kuwait oil; B—DAR blend oil; C—Arabian light oil; D—Dalia oil; E—Nemba oil; F—Castilla oil;G—Oman oil; H—Plutonio oil; I—Basrah light oil; J—ESPO oil

此外，这3套方案中：(1)到港油轮均能以最大速率卸空原油，并立即离开泊位，实现了最小油轮滞期费用的目标；(2)长输管线分别停输了22.49 h、8.52 h和6.32 h，因此这3套长输管线运输方案的优化性能按Single、Rolling_S 和 Rolling_S_C 顺序依次提高；(3)蒸馏装置加工总量分别为345000、341550、341539 m3，因此这3套蒸馏装置加工方案的优化性能依次下降，但幅度较小，相比Single模型方案，Rolling_S 和 Rolling_S_C 模型的优化性能分别只下降了1%和1.003%。综合比较，Rolling_S 和 Rolling_S_C 模型方案要优于Single模型方案。

分析产生方案优化性能差异的主要原因：(1)在耗时7112 s后Single模型的GAP值仍为2%，一方面求解速率较低所造成的优化损失，另一方面可能是8个时间段的模型设置不能实现储罐的灵活操作，进而影响了方案的优化性能，因此Single模型方案并不是全局最优方案；(2)将整个调度周期划分为离散的多个子周期，不同程度地影响了方案的全局优化性，因此很难保证 Rolling_S 和 Rolling_S_C 模型能编制出最优的储运方案。(3)“滚动时域安全约束”在一定程度上起到了保护模型方案优化性的作用，因此 Rolling_S_C 模型的总体方案略优于 Rolling_S 方案。

5 结 论

(1)以一个涉及长输管线、转油线和中转罐的复杂储运流程的中国某沿海炼油企业为原型，建立了一个完整新型的原油储运MILP模型。该模型以固定混合原油调合比例为基础，利用线性约束代替非线性约束限制混合原油品质，并且考虑了长输管线顺序输油的特点；采用滚动时域分解策略，通过设置“安全时间片段”和“安全约束”来保证分解模型的可行性和优化性。

(2)为案例企业编制未来240 h和720 h的原油输送方案，数据显示，Rolling_S 和 Rolling_S_C 模型均能在较短时间(270.16 s/240 h、159.9 s/240 h和903.81 s/720 h、806.64 s/720 h)内优化出较优储运方案。因此，所开发的基于滚动时域分解策略的原油储运MILP模型可用于处理长周期大规模原油调度问题。