考虑蜡沉积的深水油井井筒温度压力场模型

余 意， 苏剑波， 徐 斐， 孟文波， 任冠龙， 刘 凯， 高永海， 于 鑫

( 1. 中海石油(中国)有限公司 湛江分公司，广东 湛江 524057; 2. 中国石油大学(华东) 石油工程学院，山东 青岛 266580; 3. 清华大学 深圳研究生院，广东 深圳 518055 )

0 引言

油气测试和生产过程中，蜡沉积对井筒流体的流动状态及传热特性产生影响，从而影响井筒的压力及温度分布，同时井筒的压力、温度分布对蜡的析出及沉积也产生影响[1-8]。蜡沉积层形成过程中，蜡晶从油流中析出并释放析蜡潜热，形成的蜡沉积层增加传热热阻，影响井筒的传热过程；蜡沉积层厚度不断增大，减少油管的有效流通面积，使流体流速增加，且蜡沉积层改变油管内壁的粗糙度，导致摩擦压降变化，影响井筒的压力分布；井筒温度压力分布又影响蜡溶解度梯度、径向温度梯度等，从而影响析蜡量及蜡沉积速率。因此，当井筒存在蜡沉积现象时，井筒的温度和压力分布与蜡的析出及沉积是相互影响、相互耦合的关系，预测井筒的蜡沉积时需要综合考虑井筒温度、压力场和蜡沉积的关系。

为研究蜡沉积对管道及井筒的流动状态及传热特性影响，SINGH P 等[9]计算不同隔热油管下入深度条件下的井口温度及蜡沉积厚度，以及蜡沉积对原油产量的影响。基于能量平衡方程，DUAN J等[10]考虑焦耳—汤姆逊效应影响，以及蜡结晶沉积过程中析蜡潜热对流体比热变化的影响，推导含蜡油—气多相管流的显式温降公式，用于预测含蜡油—气管道的温度分布。HAJ-SHAFIEI S等[11]建立含蜡原油在液相紊流条件下管道的稳态传热模型，对热流和冷流流态的沉积厚度、蜡质混合物温度、压降和热损失率进行预测。WANG Z等[6]考虑水合物结晶放热及水合物层热阻的影响，建立一个水动力学—热力学—水合物耦合计算模型。HASAN A R等[12]预测钻完井、生产、测试等阶段井筒温度场，提出一种统一的分析井筒传热的方法，建立可适用于单流道管路和多流道管路的温度计算模型。李朋等[13]建立双管水平井井筒与油藏耦合数值模型预测注气井筒沿程温度。张立刚等[14]计算分析有杆泵抽油井在采液及热洗过程中井筒温度场的分布。根据含蜡原油在析蜡点温度、最大比热容温度划分的3个不同温度区域的比热容表达式，王海琴[15]推导考虑原油析蜡潜热影响的含蜡原油热输管道沿程温度分布的计算公式。许康等[16]考虑温度降低时含蜡原油蜡结晶放热的特征，建立使用焓法方程计算埋地热油管道停输后温降过程的预测模型。根据含蜡原油黏弹性变化特点，李传宪等[17]提出划分管道停输过程不同温降阶段的方法。王龙[18]将相变潜热处理为原油的附加比热容，得到埋地原油管道二维径向温度分布。刘晓燕等[19]考虑析蜡潜热的影响，建立架空热油管道停输后径向传热的物理和数学模型。周刚等[20]研究多种影响热油管道总传热系数的因素，认为可用4种量纲一系数表征总传热系数的物理特性，提出由量纲一系数构成的总传热系数预测新模型。靳文博[21]考虑沉积层含蜡量及厚度的变化对流体物性、界面温度、热阻等管道传热特性的影响，编写计算输油管道不同位置蜡沉积厚度的程序，得到不同运行时间下海底管道沿线的蜡沉积厚度分布规律。

目前，人们将析蜡潜热和蜡沉积层热阻纳入模型计算研究，主要集中于输油管道的温降计算，而对深水油井生产测试工况下，尚未有考虑蜡沉积影响的气液两相流体系下深水油井井筒温度、压力分布与蜡沉积互相影响的研究。笔者综合考虑蜡沉积与井筒流体流动及传热之间的相互影响关系，建立考虑蜡沉积影响的井筒流动与传热模型，分析蜡沉积对井筒内温度和压力的影响；结合蜡沉积模型，研究不同因素影响下井筒蜡沉积规律，为结蜡井清蜡防蜡工艺措施的优选与实施提供指导。

1 井筒温度和压力计算模型

地层产出流体沿生产管柱流动过程中，在摩擦阻力和重力的共同作用下，压力逐渐降低，当压力降低到小于井筒流体的泡点压力时，溶解于液相流体中的天然气析出，井筒流体由单液相转变为气液两相。存在蜡沉积现象井段中，蜡沉积对井筒流体的流动状态及传热特性产生一定的影响[1,3,5,10]。考虑油气相变及蜡质生成沉积和流动传热的影响，建立包括质量守恒方程、动量守恒方程及能量守恒方程的井筒多相流温压场计算模型。

建立模型过程做假设[6,22]：(1)海水及地层中温度分布已知；(2)产出流体在井筒中为一维流动；(3)地层中的传热过程为一维传热，产出流体从管中心到水泥环外壁面(海水段为隔水管外壁面)的传热过程为一维传热；(4)随流体流动析出蜡晶的密度等各项性质和油相的相同。

1.1 质量守恒方程

当蜡质在管壁沉积时，消耗液相产出流体中溶解的蜡分子，蜡沉积层的持续增长减少管柱的有效流通面积，管壁蜡沉积速率是与时间相关的。另外，受气体的可压缩性及井筒的油气相变影响，井筒流体的流动具有瞬态特征，与时间相关。

选择井筒中心线为Z轴，从井底到井口的流动方向为正方向(见图1)，建立液相和气相的质量守恒方程。

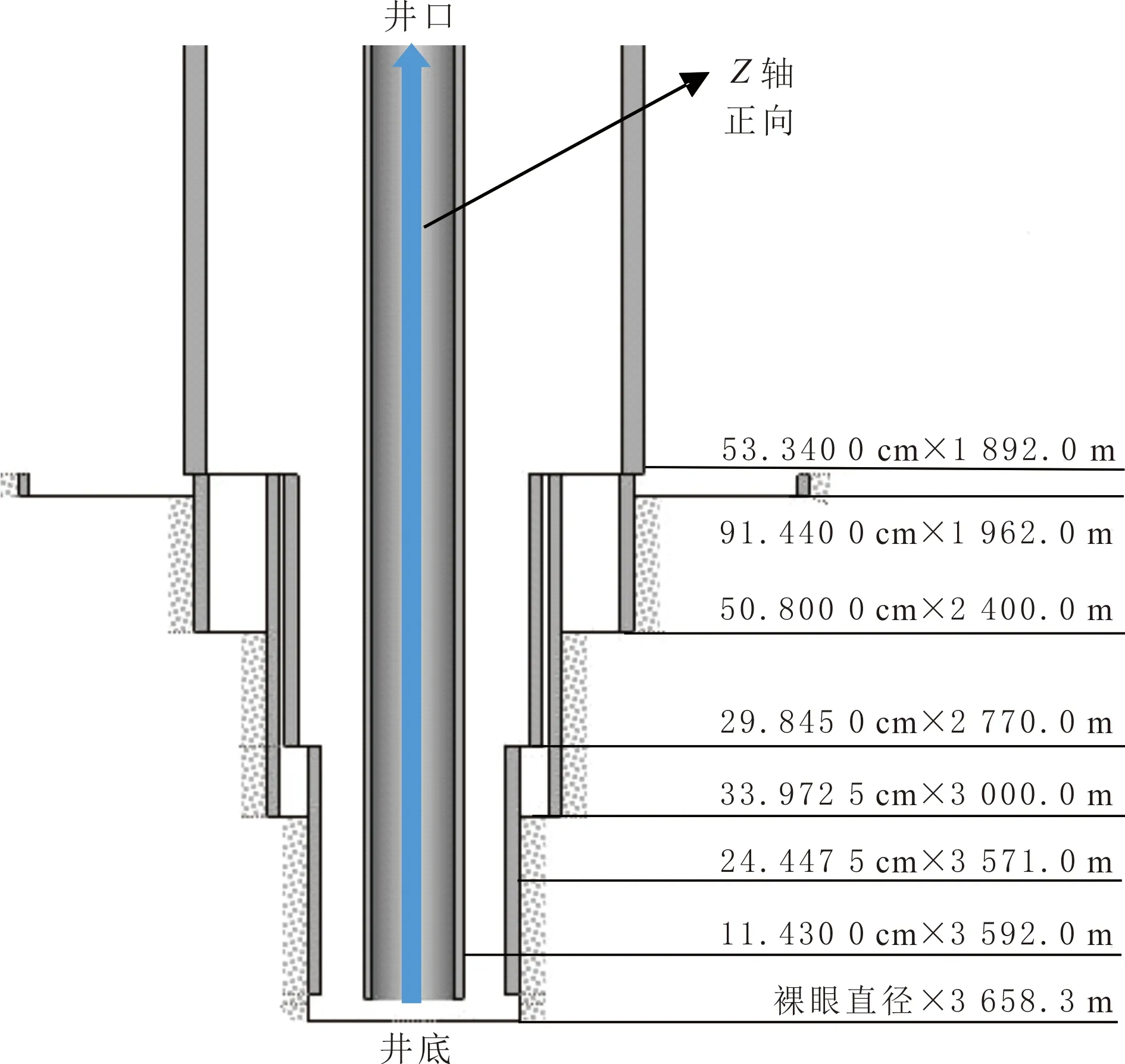
图1 某深水油井井身结构示意

液相：

(1)

气相：

(2)

式(1-2)中：A为管柱流通截面积；ρo、ρg分别为液相、气相的密度；Eo、Eg分别为液相、气相的体积分数；vo、vg分别为液相、气相的速度；ρgs为气相在标准状态下的密度；Rs为溶解气油比,采用Vasquez-Beggs公式[23]计算；Bo为油相的体积系数；M为单位时间单位长度管柱上沉积的蜡的质量，由蜡沉积动力学模型计算得到。

如果井筒内流体的压力在泡点压力以上时，则无气体逸出，井筒内流体为单液相，质量守恒方程简化为

(3)

当选择的微元段有蜡沉积时，z位置处在t时刻的流通截面积A表示为

(4)

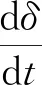
1.2 动量守恒方程

考虑蜡沉积层对井筒内流体流动的影响，建立动量守恒方程计算井筒的压力分布：

(5)

式中：p为井筒的压力；θ为井筒的井斜角；g为重力加速度；Fr为井筒的摩阻压降，采用Hasan-Kabir方法[22,24-27]求解。油井的多相流一般为泡状流和段塞流两种流型，摩阻压降求解公式为

(6)

(7)

式中：ρm为井筒流体混合物密度；vm为井筒流体混合物的速度；f为达西摩阻因数；df为管径。

由于井筒中蜡晶不断沉积，管壁管径随之变化，从而改变流速和雷诺数，摩阻因数与表面粗糙度和雷诺数有关。在计算摩阻因数时，采用文献[28]的关系式：

(8)

式中：ε为绝对粗糙度，蜡沉积前,为油管粗糙度(0.05～1.00 mm)，蜡沉积后,为蜡晶尺寸(1～3 μm)；D为管径；Re为雷诺数。

1.3 能量守恒方程

考虑有蜡沉积层后热阻变化及相变潜热影响，建立能量守恒方程计算井筒内的温度分布：

(9)

式中：Wm为混合流体的质量流量；Hf为混合流体的比焓；ΔH为蜡的结晶焓；q为单位长度井筒散失的热量。

流体的比焓梯度是温度和压力的函数，表示为

(10)

式中：Cm为混合流体的比热容；μj为流体的焦耳—汤姆逊系数；Tf为管内流体温度。

在井筒的地层段，井筒流体和地层的传热方程为

(11)

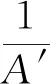
(12)

其中：Uto为井筒综合传热系数；ke为地层导热系数；rto为油管外径；TD为量纲一时间参数。

在井筒的地层段，井筒流体的传热过程为管内流体与蜡沉积层表面之间的对流传热—蜡沉积层的导热—油管的导热—油管和套管环空中的对流传热和辐射传热—套管的导热—水泥环的导热—地层段非稳态导热[29-31]。地层段井筒综合传热系数Uto的计算公式为

(13)

式中：rwax为蜡沉积层内表面直径；rti为油管内径；rci为套管内径；rco为套管外径；rwb为水泥环外径；hf为管内流体和蜡沉积层的对流换热系数；hc为环空对流换热系数；hr为环空辐射换热系数；kwax为蜡沉积层导热系数；ktub为油管导热系数；kcas为套管导热系数；kcem为水泥环导热系数。

将式(10—11)代入式(9)，可得地层段井筒内流体温度计算公式为

(14)

在井筒的海水段，井筒流体和海水的传热方程为

(15)

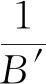
(16)

在井筒的海水段，油管中流体向外界传热过程为管内流体与蜡沉积层内表面的对流传热—蜡沉积层的导热—油管的导热—油管和隔水管环空间的对流传热和辐射传热—隔水管内的导热—隔水管外壁面和外界海水之间的对流传热。海水段井筒综合传热系数Uto的计算公式为

(17)

式中：hs为隔水管外壁和外界海水之间的对流换热系数。

将式(10、15)代入式(9)，可得海水段井筒内流体温度计算公式为

(18)

1.4 蜡沉积动力学模型

井筒及管道的蜡沉积是流体组分、流体温度、流体流速、流体与管壁温度差、流动特性及沉积时间等因素共同作用的结果[33-36]。流体组分影响析蜡点及不同温度、压力条件下的析蜡量、温度浓度梯度等参数，流体温度、流体与管壁温度差影响蜡分子扩散过程，流体流速、流动特性影响流体对蜡沉积层的剪切剥离作用，沉积时间影响温度、压力分布及沉积层凝油含量。综合考虑分子扩散、沉积层凝油含量及剪切剥离作用，采用气液两相流蜡沉积动力学模型：

(19)

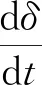
(20)

(21)

(22)

式(20-22)中：ρm为井筒流体密度；vsl为液相表观流速；vsg为气相表观流速；μm为流体黏度；k2、k3、k4、m、n为经验参数。

将式(21)代入式(19)，可得蜡沉积速率计算模型的表达式为

(23)

式中：k、a为经验参数，一般通过气液两相流条件下蜡沉积实验得到，随初始组成而变化，对某一特定组成和初始温压条件，取为k=6.23，a=1.152×10-5，n=0.77，m=2.16。由式(22)求得蜡沉积速率，对其进行时间积分，可得某一时间的蜡沉积厚度。

2 模型求解方法

2.1 初始条件及边界条件

模型求解时，初始条件为蜡沉积开始时井筒的温度和压力，井筒的温度为初始流动时的温度，压力为地面井口回压与井筒内液柱静压之和。边界条件为在一定产量条件下，井底流压不变，井底流体温度等于地层温度。

2.2 模型求解过程

采用有限差分法对建立的模型进行数值求解，求解过程：

(1)将井筒划分为若干个微元体。

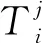
(3)假设在j时刻，微元体i出口位置的压力为pAss，温度为TAss。

(5)计算平均温度和压力下微元体内流体的密度、黏度、综合传热系数、溶解气油比等参数。

(6)根据蜡沉积动力学模型计算蜡沉积速率，以及沉积厚度、管柱管径D等参数。

(7)根据井筒温压场模型计算微元体i出口位置、j时刻的温度TCal和压力pCal。

(8)比较假设的温度TAss、压力pAss和计算的温度TCal、压力pCal，若两者的误差小于设定误差，则计算结束，TCal和pCal为实际出口的温度和压力；否则，使TAss、pAss等于TCal、pCal，重复步骤(4-7)，直至误差小于设定值。

(9)将步骤(8)计算的j时刻、微元体i出口位置的压力和温度，设置为j时刻、微元体i+1入口位置的压力和温度，重复步骤(3-8)，可得微元体i+1出口位置处j时刻的温度、压力、蜡沉积速率等参数。

(10)重复步骤(3-9)，可得整个井筒范围内j时刻的温度、压力、蜡沉积速率、沉积厚度分布，将j时刻的各参数作为初始值，重复步骤(2-9)，可得整个井筒范围内j+1时刻的温度、压力、蜡沉积速率。

3 蜡沉积影响因素

结合考虑蜡沉积的井筒温度压力场计算模型和蜡沉积动力学模型，应用现场实例对不同影响因素条件下深水油井井筒内蜡沉积速率和沉积厚度分布进行计算，并分析规律。

根据某深水油井数据，井型为直井，设计井深为3 658.3 m，水深为1 892.0 m，地温梯度为3 ℃/100 m，测试层位地层压力为40 MPa，温度为55.6 ℃，产出流体中油相密度为875 kg/m3，井身结构见图1。采用文中模型，分析考虑蜡沉积的深水油井井筒的温度和压力分布。

3.1 产量

不同产量条件下井筒蜡沉积速率和蜡沉积厚度分布见图2，沉积时间为480 h。由图2可以看出，在产量一定时，从初始结蜡点开始往上，蜡沉积速率与沉积厚度随井深的减少是先增加后减少的。第一，温度浓度梯度dC/dT在析蜡点温度附近的值很小，接近于0，超过析蜡点温度后，dC/dT随井筒流体温度的降低先增加后减少，蜡沉积速率也随流体温度的降低先增加后减少(见图3)；第二，井筒流体向上流动的过程中，流体温度降低，外界环境温度在地层段降低，在海水段增加，发生蜡沉积的区域主要是在海水段，流体和与外界环境之间的温度差随井深的减少而逐渐减少，径向温度梯度dT/dr随井深的减少而逐渐减少，蜡沉积速率与dT/dr呈正相关关系；第三，在靠近井口位置压力降低，气体从液相中大量析出且膨胀，导致流体的流动速度增加，增强流体对管道壁面上蜡沉积层的剪切剥离效果，从而导致蜡沉积层的沉积速率和沉积厚度减小。

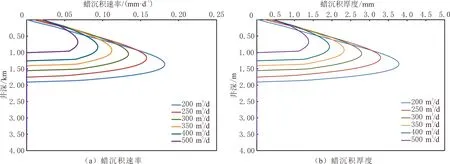
图2 不同产量条件下井筒蜡沉积速率和蜡沉积厚度分布

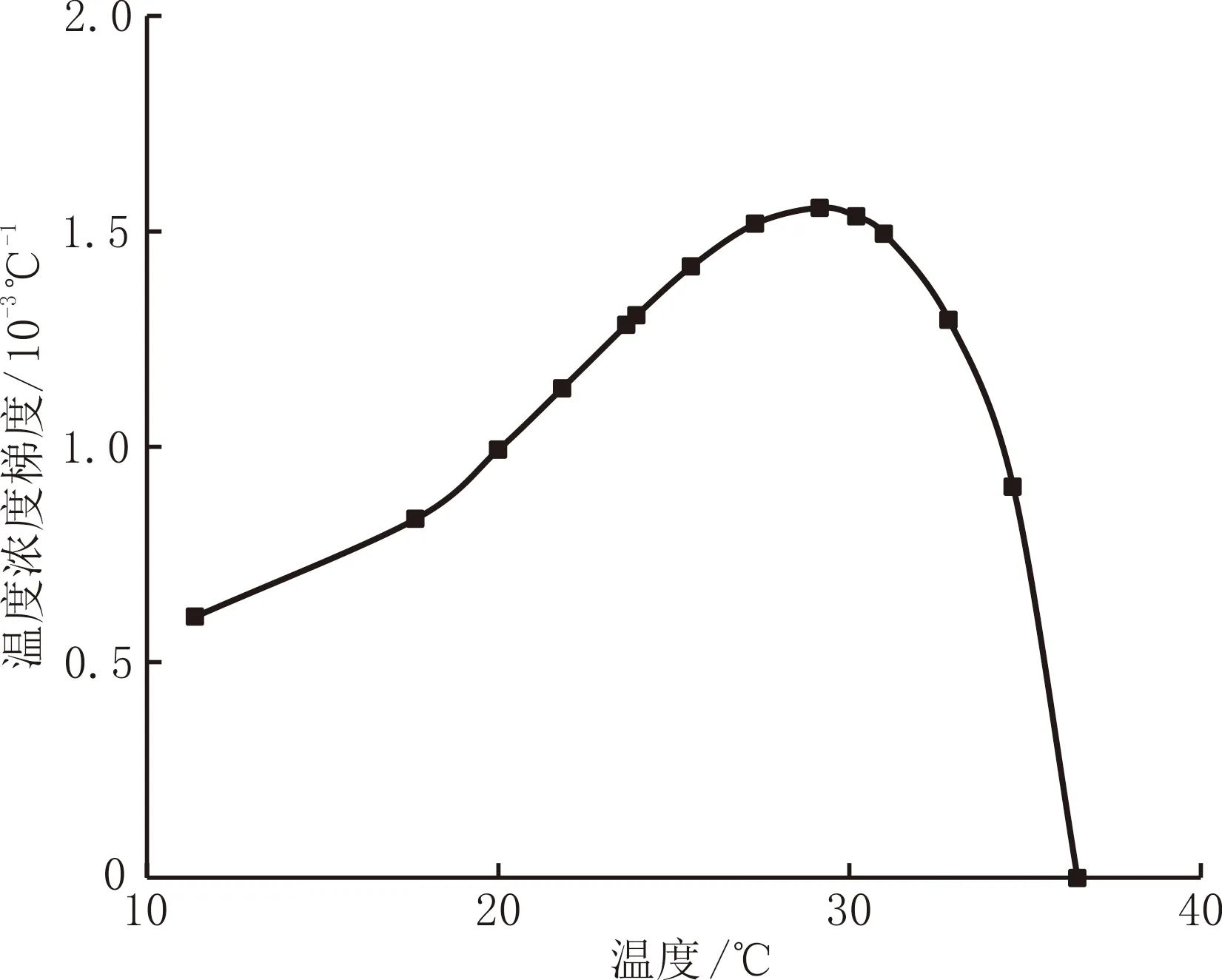
图3 蜡的温度浓度梯度与温度曲线

由图2还可以看出，随产量增加，蜡沉积区域减少，最大蜡沉积速率与沉积厚度减少，最大蜡沉积速率与沉积厚度出现的位置上移，蜡沉积速率与沉积厚度沿井深从下往上随产量的增加呈现先减少后增加的规律。原因在于产量越大，流体流速越大，井筒流体越保持较高的温度，与外界环境之间的温度差越大，dT/dr越大，导致蜡沉积速率与沉积厚度增加；流体流速越大，管壁处的剪切力越大，对管壁上蜡沉积层的剪切剥离作用越强，蜡沉积速率与沉积厚度减少；产量越大，井筒流体的温度越高，dC/dT和蜡沉积速率先增后减少。

在井筒蜡沉积过程中，多种因素的作用同时发生，在沉积区域下部，由流速增加引起的剪切剥离作用和温度浓度梯度起主导作用；在靠近井口处，径向温度梯度和温度浓度梯度起主要作用。

3.2 地温梯度

不同地温梯度条件下井筒蜡沉积速率、蜡沉积厚度分布见图4。由图4可以看出，随地温梯度增加，蜡沉积区域上移，最大蜡沉积速率与沉积厚度出现的位置也上移，最大蜡沉积速率与沉积厚度减少。地温梯度越高，地层段环境温度越高，井筒流体的温度越高，径向温度梯度也越大，蜡沉积区域上移；随井筒流体温度的增加，dC/dT先增加后减小(见图3)；井筒流体的温度降低到最大温度浓度梯度dC/dT时的位置越靠近井口，环境温度越高，径向温度梯度越小。上述因素共同作用的结果是最大蜡沉积速率与沉积厚度出现的位置上移，最大蜡沉积速率与沉积厚度减少。

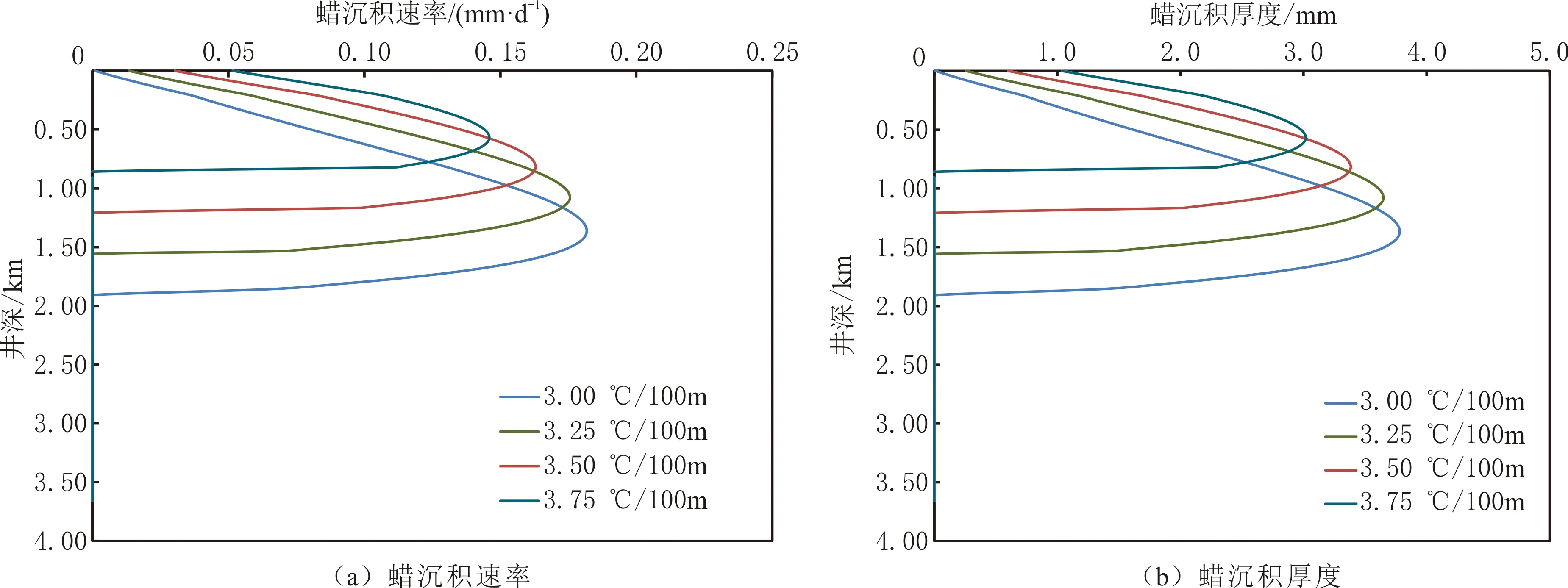
图4 不同地温梯度条件下井筒蜡沉积速率和蜡沉积厚度分布

3.3 管柱内径

不同管柱管径条件下井筒蜡沉积速率、蜡沉积厚度分布见图5。由图5可以看出，随管柱管径增加，蜡沉积速率与沉积厚度减少。一方面，管柱管径增加，管柱流体流速减少，减弱管柱流体与管壁之间的对流传热，管壁径向温度梯度dT/dr减少，蜡沉积速率与沉积厚度也减少；另一方面，管柱管径增加，流通面积增加，流体流速减少，管壁处剪切力减少，流体对蜡沉积层的剪切剥离作用减弱，蜡沉积速率与沉积厚度增加。

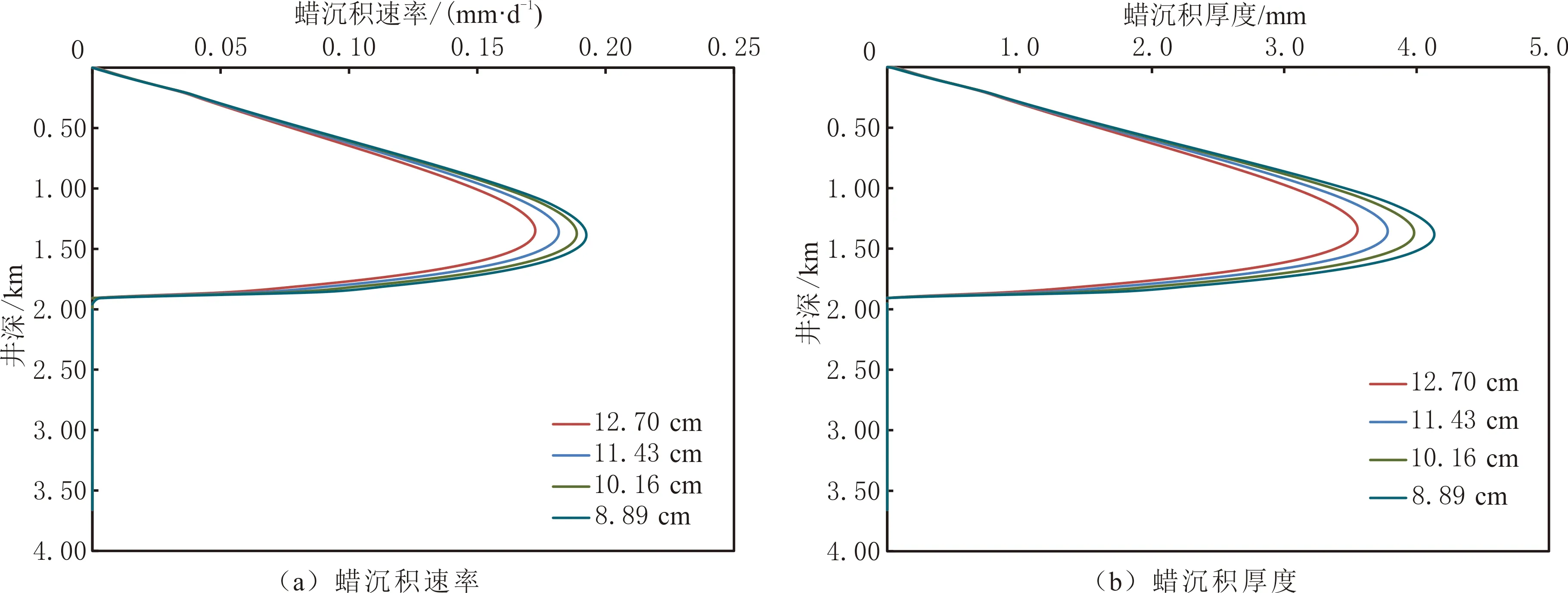
图5 不同管柱管径条件下井筒蜡沉积速率和蜡沉积厚度分布

4 井筒温度、压力场分布影响

4.1 蜡沉积时间

为分析蜡沉积时间对井筒流体温度和压力的影响，考虑流体组分条件，流体析蜡点为45 ℃，当井筒流体温度低于析蜡点时，存在蜡沉积，计算的初始蜡沉积速率为1.50 mm/d。不同蜡沉积时间条件下井筒流体温度和压力分布见图6。由图6可以看出，随蜡沉积时间增加，井筒中蜡沉积区域的流体温度随之增加，井筒流体的压力基本不变。初始时刻，井口温度为21.92 ℃，沉积480 h后，井口温度增加到25.59 ℃。一方面，随沉积时间增加，井筒中蜡沉积层厚度增加，传热热阻也增加，对井筒流体起到一定的保温作用；油流中的蜡的析出是一个放热的过程，蜡晶析出释放的析蜡潜热相当于内热源，也增加井筒流体的温度。另一方面，管壁上的蜡沉积层减少管柱的流动截面积，流体流速增加，影响流体与蜡沉积层内表面的对流传热过程，也增加流动过程中的摩阻压降，降低井筒流体的压力，受流速相应增加和温度升高的共同作用，蜡沉积速度逐渐降低，蜡沉积厚度逐渐趋于平衡，摩阻压降下降有限；并且由于流体温度的升高降低流体黏度，减少摩阻压降，相比于重力压降，摩阻压降在总压降中所占比例较少。因此，随蜡沉积时间增加，井筒流体的压力变化并不大。

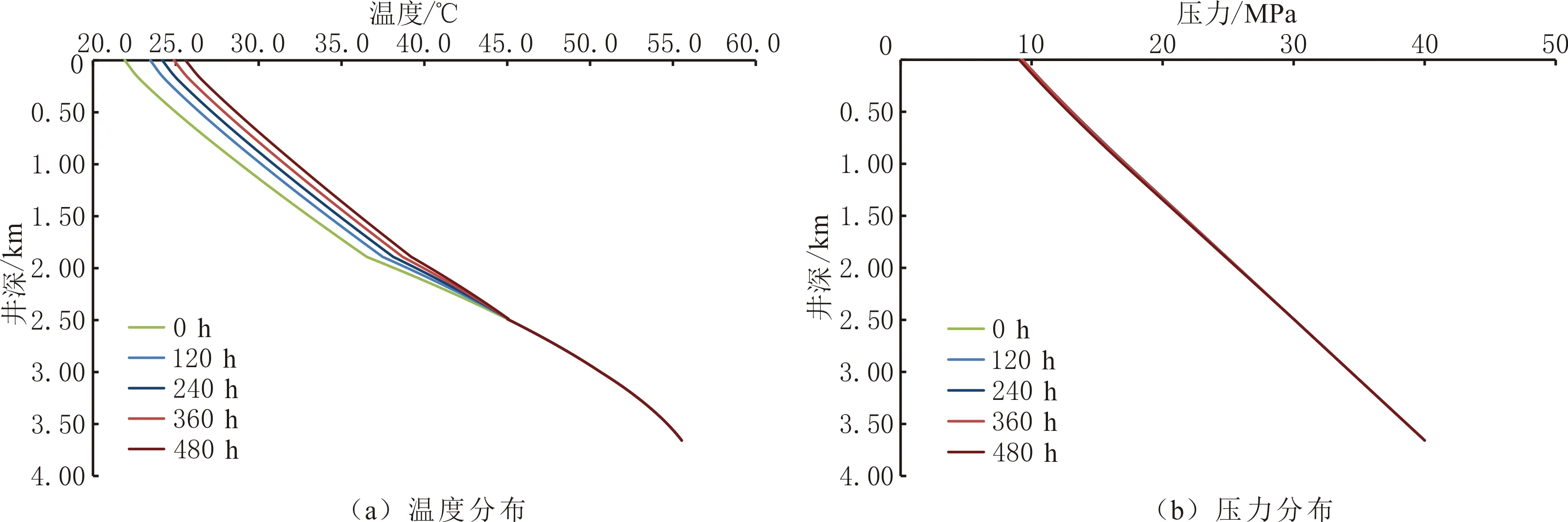
图6 不同蜡沉积时间条件下井筒流体温度和压力分布

4.2 蜡沉积速率

不同蜡沉积速率条件下井筒流体温度和压力分布见图7。由图7可以看出，随蜡沉积速率增加，井筒中蜡沉积区域的流体温度随之增加，井筒流体的压力基本不变。若无蜡沉积发生，井口温度为21.92 ℃，当初始蜡沉积速率增加到2.00 mm/d时，井口温度增加到24.82 ℃。

当蜡沉积时间相同时，随沉积速率增加，管壁上的蜡沉积层厚度增加，第一，蜡沉积层增加使传热热阻增加，对井筒流体起到一定的保温作用；第二，管壁上的蜡沉积层减少管柱的流动截面积，使产出流体流速增加，影响产出流体与蜡沉积层表面的对流传热过程；第三，蜡晶析出释放的析蜡潜热也增加井筒流体的温度，且蜡沉积速率变化，析蜡潜热释放速率也是变化的，对井筒流体的温度有一定的影响。

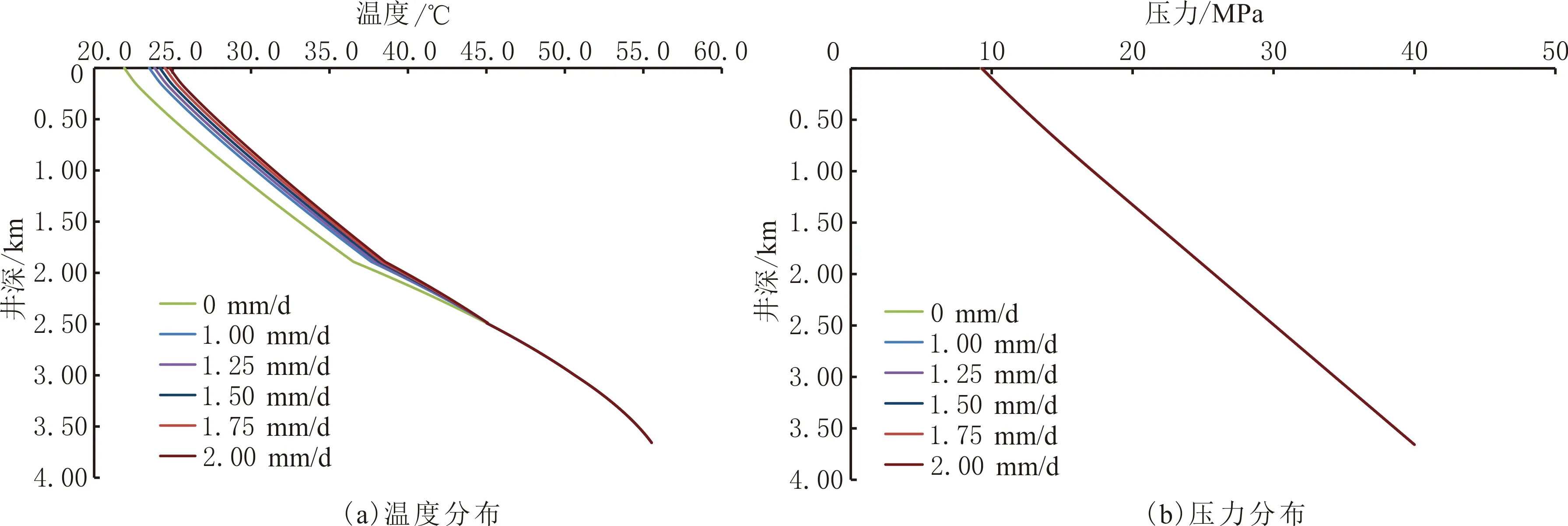
图7 不同初始蜡沉积速率条件下井筒流体温度和压力分布

5 结论

(1)综合考虑蜡沉积与井筒流体流动、传热之间的耦合关系，建立考虑蜡沉积的井筒温度、压力场计算模型，在质量守恒方程中，考虑蜡晶析出及气体逸出的影响；在动量守恒方程中，考虑管壁蜡沉积厚度变化引起的截面积、流速变化对压降的影响；在能量守恒方程中，考虑蜡沉积引起的析蜡潜热、管壁蜡沉积层导致的综合传热系数的变化，能够更为准确预测井筒温度、压力分布。

(2)沉积时间越长，初始沉积速率越大，井筒温度越高，随沉积速率逐渐降低，摩阻压降占比较小，井筒总压力变化不大。

(3)随产量增加，最大蜡沉积层厚度与沉积速率出现的位置上移，最大蜡沉积层厚度与沉积速率减少，蜡沉积层厚度与沉积速率沿井深从下往上呈现先减少后增加的趋势；随地温梯度增加，最大蜡沉积速率与沉积厚度出现的位置上移，最大蜡沉积速率与沉积厚度减少；随管柱管径增加，蜡沉积速率与沉积厚度减少。