能量消耗均衡的水下传感器网络非均匀分簇算法
2021-05-20魏连锁陈齐齐
魏连锁, 吴 迪, 李 华, 苏 扬, 韩 建, 陈齐齐
( 齐齐哈尔大学 计算机与控制工程学院,黑龙江 齐齐哈尔 161006 )
0 引言
水下传感器网络是利用水下传感器节点感知水下相关信息,通过水声通信媒介将传感器节点感知的数据信息传送至数据处理中心[1-4]。水下传感器网络广泛应用于水下资源勘探、海洋地理数据收集、导航和控制、灾难预防、军事安全等领域[5-8]。由于水下传感器节点自带电池能量有限,水声信号的传输受水下复杂环境影响较大,水声通信带宽有限、多径效应严重,水声信号易受非平稳噪声等因素的影响[9-11],将水下节点长时间部署后,有效的能量供给对于整个水下传感器网络至关重要[12-15]。
有关能量高效的传感器网络研究方面,HEINZELMAN W R等[16]提出自适应低功耗的LEACH算法,使用基于轮的传感器网络进行拓扑重构,利用概率函数选择簇头。该算法未考虑簇头分布不均及每簇的大小不同,易导致簇头能量消耗不均而过早死亡。QING L等[17]将节点能量异构与LEACH协议相结合,优化改进后提出DEEC算法,对簇头阈值函数参数进行动态调整,与LEACH算法相比,网络的寿命较长,但节点的能量消耗很高。DOMINGO M C等[18]提出分布式水下聚类算法(DUCS),不使用泛洪技术,最大限度减少节点之间的消息交换,降低节点的能量消耗。为了解决基站附近簇头节点负载过重的“热点”状况,李成法等[19]提出高能效的非均匀分簇算法(EEUC),根据簇头和基站之间的距离调整簇的大小,使网络中接近基站的簇规模变小,提高簇头能量消耗均衡的效果。雷辉等[20]提出水声传感器网络多跳非均匀分簇算法(EEMUC),根据节点和基站之间的距离,将整个网络划分为以基站为中心的不均匀弧形分层模型;每个层的节点根据综合属性值选择簇头,减小靠近基站的簇;簇之间采用多跳数据传输,有效均衡簇头的能量消耗。WANG K等[21]提出用于数据传输的分簇算法(EGRCs),将整个三维网络分成若干网格, 每个网格组成一个簇,选择剩余能量最大、到基站距离最短的节点作为簇头,根据剩余能量、端到端延迟及节点到基站的距离,选择下一跳簇头节点。该算法能够延长网络寿命,提高能量使用效率,但未考虑节点分布不均对网络生存时间的影响。蒋华等[22]提出基于改进灰狼优化的分簇算法,利用改进适应度函数的灰狼优化算法进行分簇,有效延长网络的生存时间。李志华等[23]提出基于等级划分的分簇算法(UCUBG),根据节点剩余能量和节点密度选择簇头,再根据簇头之间的位置关系划分簇头等级,最后节点选择负载最小的簇头入簇。该算法忽略簇头剩余能量对簇头等级划分的影响,在选择簇头时仅考虑某一区域内节点的邻居节点个数,未考虑邻居节点与该节点的距离对节点密集程度的影响。
笔者提出一种能量消耗均衡的水下传感器网络非均匀分簇算法(EBUC),解决水下传感器网络节点分布不均导致各节点能量消耗不均的问题。考虑节点数量及节点到邻居节点距离,构造节点密集度权重函数,使簇头在网络中分布更均匀,每轮选择的簇头个数变化较小,算法稳定性更好;在划分簇头等级时,考虑簇头的剩余能量和簇头到基站的距离,选择簇头的通信半径,更合理地划分簇头等级,减少簇头的能量消耗;普通节点选择簇头建立成簇, 构建一种能量消耗均衡、高效的水下传感器网络。该算法有效解决非均匀分簇方式下簇头能量消耗不均的问题,节省网络中每个节点的能量消耗,延长网络使用寿命。
1 系统模型
1.1 网络模型
应用3D水下传感器网络作为网络模型[24]。传感器网络G=(S,L),其中S=(S1,S2,…,SN),Si为网络里的第i个节点,N为节点个数;L={L(i,j),Si∈S,Sj∈S,i≠j},L(i,j)为节点Si至Sj的通讯线路。
1.2 能量消耗模型
应用无线通信的能量衰减模型[25],节点发送数据包的能量消耗Et(d)为
Et(d)=λtlA(d),
(1)
A(d)=dηad,
(2)
(3)
(4)
式(1-4)中:λt为发送能量消耗因数;l为数据包长度;d为发送节点到接收节点的距离;A(d)为发送距离为d时消耗的能量;η为能量衰减因数,且η=1.5;a(f)为吸收因数;f为信号频率。
节点接收数据包的能量消耗Er为
Er=λrl,
(5)
式中:λr为接收能量消耗因数。
2 EBUC算法
2.1 节点密集度
传感器网络的节点随机分布,网络中各区域的节点密集度差别较大。若不考虑节点密集度,在选择簇头时,可能出现节点密集度大的区域簇头个数较少的问题。簇头不仅传输自身收集的数据,还要转发其他簇头的数据,簇头较少导致簇头能量消耗过高而过早死亡。因此,在选择簇头时,需要考虑节点密集度对能量消耗均衡的影响。节点密集度的决定因素:一是固定区域内节点个数;二是节点与邻居节点间的距离。引入节点密集度权重的概念,考虑两个因素对节点密集度的影响,节点密集度权重Di为
(6)
式中:M为节点Si的邻居节点数量;d(Si,Sm)为节点Si到邻居节点Sm的距离。由式(6)可知,网络中节点密集度由邻居节点数量和邻居节点到该节点的距离决定,邻居节点数量越多、到该节点的距离越近,节点密集度越大。
2.2 分簇过程
分簇算法中簇头转发簇内节点的数据,由于传输负载较大,需要由剩余能量较高的节点担任簇头。传感器网络的节点通常随机分布,在选择簇头时要考虑不同区域的节点密集度。因此,应考虑节点剩余能量、节点密集度、节点到基站的距离选择簇头,通过节点通信半径调整优化簇头等级的划分,根据簇头的权值函数,节点选择均衡簇间负载效果最好的簇头入簇。
2.2.1 选择候选簇头
受洋流影响,水下随机部署的节点位置发生变化,导致网络中不同区域的节点密集度差异很大。选择候选簇头时,需要考虑节点附近邻居节点的剩余能量和节点密集度对簇头能量消耗的影响,构造节点阈值函数T(i)为
(7)
式中:Er(i)为节点Si的剩余能量;Eav(i)为节点Si在通信半径内所有节点的平均剩余能量;Dmax为整个网络中节点的最大密集度权重;a1、b1和c1为调节因数,且a1+b1+c1=1。由式(7)可知,节点的剩余能量越多、节点密集度越高,节点阈值函数越大,选择节点作为候选簇头的概率越高。
2.2.2 确定簇头
在多跳传感器网络中,靠近基站的簇头需要传输其他较远簇头的数据,因此靠近基站的簇头能量过度消耗而过早死亡。同时,受洋流等因素影响,水中节点位置不固定,还要考虑某区域节点的密集度。考虑候选簇头到基站的距离和节点密集度调整竞争半径,使距离基站近、节点密集度高的候选簇头的竞争半径变大。候选簇头的竞争半径Rc(i)为
(8)
式中:d(Si,ds)为节点Si到基站ds的距离;Rmax为最大通信半径;dmax、dmin分别为网络中节点与基站之间的最大距离和最小距离;a2、b2为调节因数,且a2+b2=1。由式(8)可知,候选簇头与基站距离越近、节点密集度越高,候选簇头的竞争半径越小,在节点入簇时其他节点加入该簇的数量越少。
计算竞争半径后,候选簇头根据剩余能量选择何时向全网广播竞选为最终簇头的消息。候选簇头在竞选簇头失败后退化为普通节点,与剩余的其他节点在节点入簇阶段选择合适的簇头入簇。
2.2.3 划分簇头等级
为了使簇间的通信代价与通信时延最小,通常要划分簇头的等级。根据UCUBG算法[24],划分簇头等级时考虑簇头间的相对位置,使深度不同的簇头始终保持等级差,避免深度相近的簇头划分为相同等级,使相同等级的簇头传输负载差异过大。该算法在划分簇头等级时未给出如何选择簇头的通信半径。
考虑簇头到基站的距离和簇头剩余能量的通信半径函数调整簇头的通信半径,使距离基站较近且剩余能量较高的簇头更容易成为高等级的簇头,更合理划分簇头的等级。簇头的通信半径Ro(j)为
(9)
式中:d(Sj,ds)为簇头Sj到基站ds的距离;E0(j)、Er(j)分别为簇头初始能量和剩余能量;a3、b3为调节因数,且a3+b3=1。由式(9)可知,簇头的剩余能量越多、与基站的距离越近,簇头的通信半径越大,在划分簇头等级时成为较高等级簇头的概率越大。
2.2.4 节点入簇
考虑节点到簇头的距离、簇头到基站的距离、簇头的剩余能量、簇头等级、簇的大小等因素,均衡各簇头的能量消耗。构造节点入簇的权值函数Wj(Si,Sj),普通节点选择均衡能量消耗效果最好的簇头入簇。节点入簇公式为
(10)
式中:d(Si,Sj)为节点Si到簇头Sj的距离;Ri为节点i的通信半径;Gj为簇头的等级;Gmax为簇头的最高等级。a4、b4、c4和d4为调节因数,且a4+b4+c4+d4=1。由式(10)可知,簇头的权值函数越小,节点选择该簇头入簇的概率越大。
2.3 算法伪代码
EBUC算法伪代码见表1。

表1 EBUC算法伪代码
选择候选簇头阶段:网络中所有节点在通信半径R内广播自身的初始能量E0(i)、剩余能量Er(i)及节点位置坐标(xi,yi,zi),节点Si接收其他节点广播的信息后,通过式(7)得到Si的阈值函数T(i)。每个节点选择 (0,1)之间的随机数μ。如果T(i)>μ,则选择该节点作为候选簇头。
确定簇头阶段:候选簇头在通信半径R内广播自己竞选为候选簇头的信息TEMPORARY_HEAD_MSG,信息内容包含簇头的竞争半径Rc(i)、簇头剩余能量Er(i)及簇头的唯一标识id。候选簇头根据收到的信息建立邻居簇头集合Sch(i),节点与邻居簇头集合中剩余能量更高的节点进行比较,决定是否选为簇头。若Si剩余能量高于邻居簇头集合中所有节点的剩余能量,则选择该节点为最终簇头,并广播信息FINAL_HEAD_MSG通知邻居簇头;若Si接收到Sj竞选为簇头的信息,同时Sj在集合Sch(i)里, 那么Si退出选举,并广播信息QUIT_ELECTION_MSG通知邻居簇头;若Si接收到Sj发来的退出选举的消息,同时Sj在集合Sch(i)里,则Si将Sj从集合Sch(i)中删除。
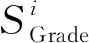
节点入簇阶段:由式(10)计算簇头和未被选为簇头的节点的权值,比较所有簇头的权值,节点选择权值最小的簇头入簇。
3 算法仿真与分析
通过仿真实验验证EBUC算法的特性,在Python3.7平台上,将EBUC算法与UCUBG、EEUC和LEACH算法进行对比。仿真实验参数见表2。

表2 仿真实验参数
3.1 算法稳定性
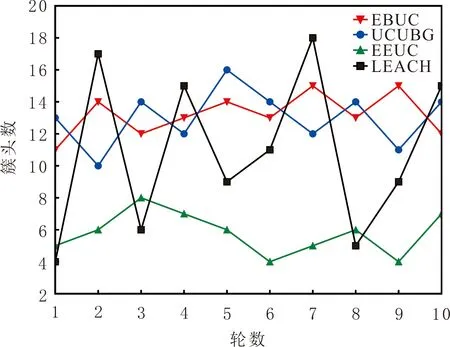
图1 4种算法选出的簇头数
非均匀分簇算法的稳定性主要由每轮选出的簇头数量决定,簇头数量的变化范围越小,网络的稳定性越高。选取100个初始节点进行实验,随机选择10轮,4种算法选出的簇头数量变化见图1。由图1可知,各算法选出的簇头数量的变化范围为nLEACH=[4,18],nEEUC=[4,8],nUCUBG=[10,16],nEBUC=[11,15]。
与 LEACH 算法相比,EEUC、UCUBG和 EBUC算法稳定性更好,尤其是 EBUC算法的稳定性最为明显。LEACH算法应用概率函数选择簇头,不能保证簇头数量的稳定性;EEUC算法在选择簇头时考虑节点与基站的距离,比LEACH算法稳定性更好,但未考虑平均剩余能量对簇头选择的影响,簇头数量比UCUBG和 EBUC算法的少;UCUBG和 EBUC算法考虑更多因素的影响,有效延长网络的生存时间,与 UCUBG算法相比,EBUC算法在选择簇头时,考虑邻居节点数量、节点与邻居节点距离及节点密集度权重函数,使网络中簇头的分布更均匀,算法稳定性更好。
为了直观对比不同算法簇头数量的变化情况, 对4种算法每轮簇头数量的标准差进行对比(见图2)。由图2可知,LEACH算法的簇头数量标准差比其他3种算法的大,EEUC、UCUBG和EBUC算法的簇头数量标准差比较接近,说明LEACH算法的稳定性最差,EEUC、UCUBG和EBUC算法的稳定性比较接近,尤其是EBUC算法簇头数量标准差最小,稳定性最好。
3.2 能量消耗均衡性
数据传输时簇头比其他节点消耗的能量更多,需要均衡簇头的能量消耗,才能避免簇头的过早死亡。随机选择10轮,4种算法的簇头能量消耗标准差见图3。由图3可知,LEACH算法的簇头能量消耗标准差最大,EEUC、UCUBG和EBUC算法的簇头能量消耗标准差相似,尤其是EBUC算法的最小,表明LEACH算法均衡网络能量消耗的效果最差,EBUC算法均衡网络能量消耗的效果最好。
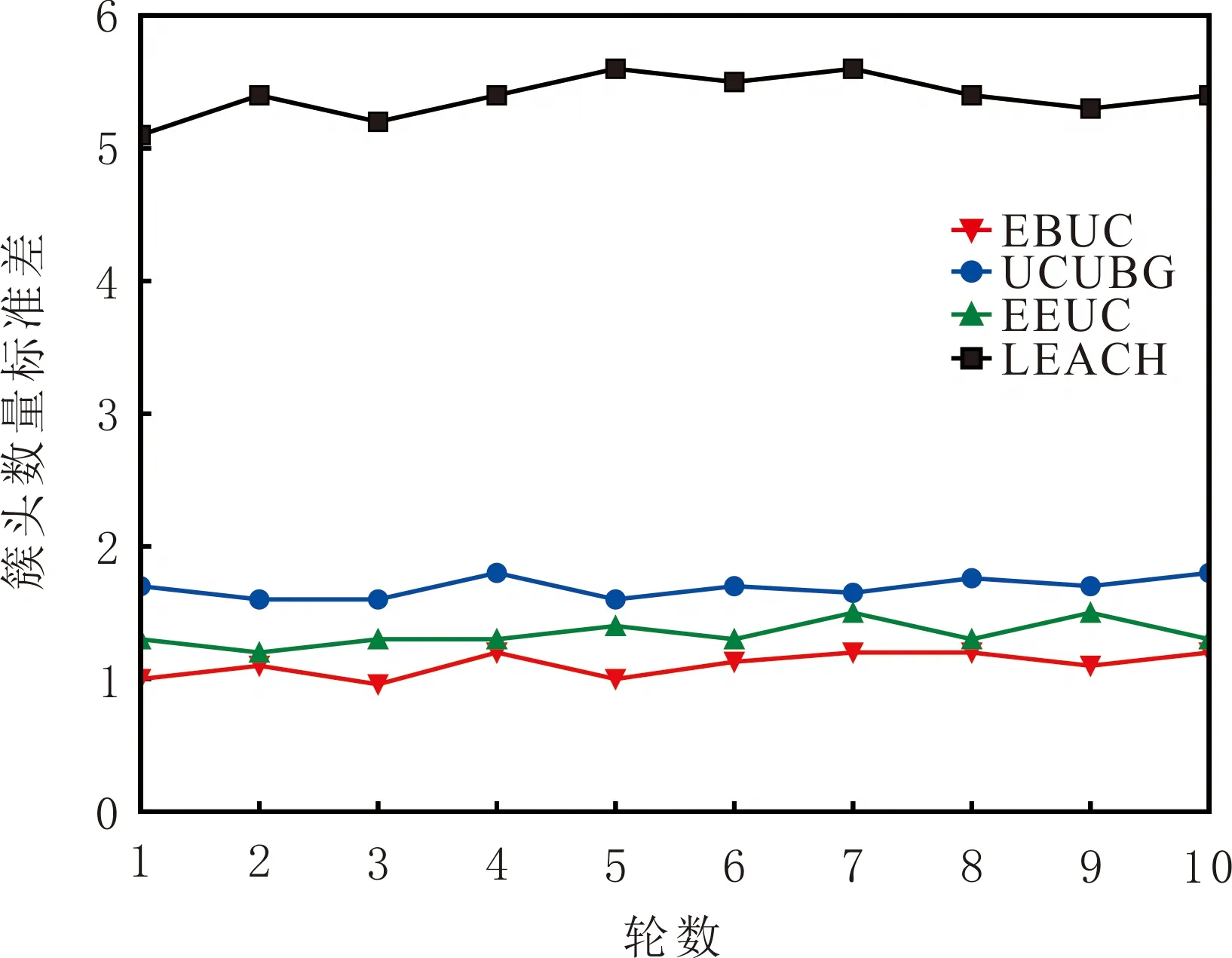
图2 4种算法的簇头数量标准差
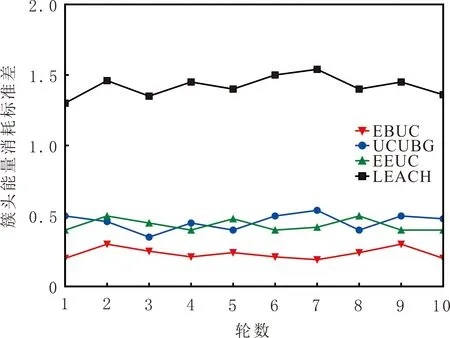
图3 4种算法的簇头能量消耗标准差
网络中节点的平均剩余能量可以有效反映网络能量消耗的均衡性。前20轮4种算法节点的平均剩余能量变化见图4。由图4可知,EBUC算法节点的平均剩余能量最多,在均衡网络能量消耗方面效果最佳。
3.3 网络使用寿命
当节点数为50、75、100、125、150、175和200个时,4种算法的首个死亡节点出现轮数见图5。由图5可知,EBUC算法的首个死亡节点出现的轮数大于其他3种算法的,可以有效延长网络使用寿命。
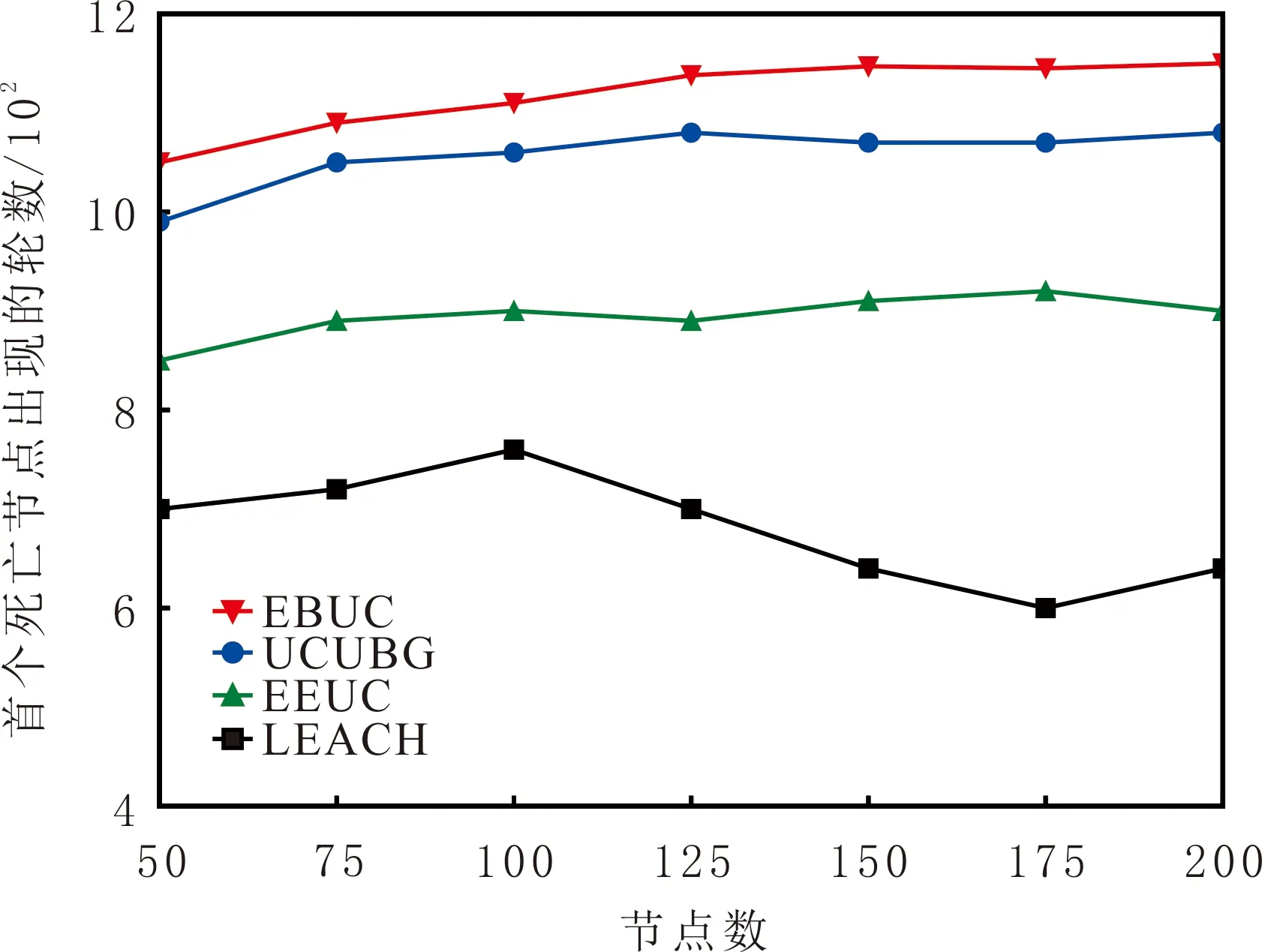
图4 4种算法节点的平均剩余能量
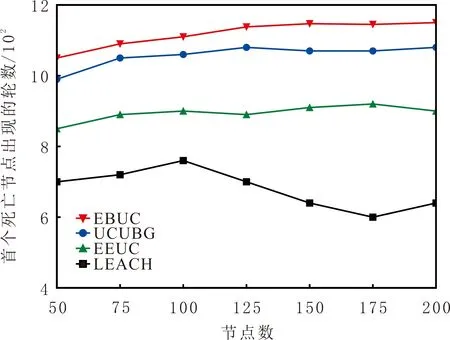
图5 4种算法的首个死亡节点出现轮数
4种算法的存活节点数见图6。由图6可知,EBUC算法的首个死亡节点出现的轮数是LEACH算法的245%、EEUC算法的168%、UCUBG算法的112%,EBUC算法均衡能量消耗效果最好。 LEACH算法应用概率函数选择的簇头分布不均匀且簇头的能量损失差异大,导致死亡节点首先出现;EEUC算法在选择簇头时频繁交换信息,使节点负载过大而过早死亡;UCUBG和EBUC算法在网络接近死亡时,短时间内节点基本同时死亡,表明UCUBG和EBUC算法节点能量消耗比较均衡,但EBUC算法网络的生存时间比UCUBG算法的更长。
4种算法的网络生命周期见图7。由图7可知, LEACH和EEUC算法的死亡节点数随时间变化较大,UCUBG和EBUC算法的节点死亡规律基本一致、变化比较稳定。EBUC算法的节点存活时间比其他3种算法的更长,表明EBUC算法有效延长网络的生存时间。
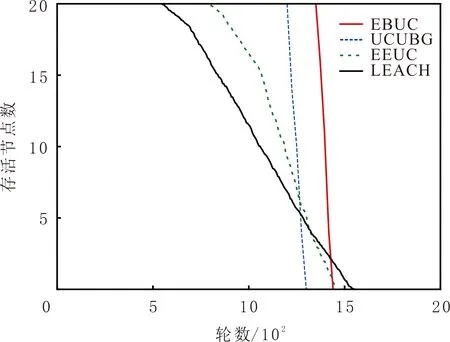
图6 4种算法的存活节点数
4 结论
(1)对于水下传感器网络节点分布不均导致节点能量消耗不均的问题,提出能量消耗均衡的水下传感器网络非均匀分簇算法(EBUC)。引入节点密集度权重函数,考虑节点剩余能量及节点到基站的距离选择簇头,使簇头在网络中分布更均匀;考虑簇头的剩余能量和簇头到基站的距离,选择簇头的通信半径,更合理划分簇头等级。
(2)EBUC算法具有稳定性和能量消耗均衡性,能够有效均衡簇头的能量消耗,减少网络能量损失,延长网络使用寿命。
(3)水下传感器网络能量消耗不均,相比陆地水下传输时延更大,对水下通信数据传输时延还需进一步研究。
