考虑启动压力梯度的致密油藏不稳定试井解析方法

樊冬艳， 曾 慧， 姚 军， 孙 海， 赵 杰， 牛 娜

( 1. 中国石油大学(华东) 石油工程学院，山东 青岛 266555； 2. 中国石化西南油气分公司 采气一厂，四川 德阳 618000； 3. 东方电气集团 东方电机有限公司，四川 德阳 618000； 4. 中国石化西南油气分公司 勘探开发研究院，四川 成都 610041 )

0 引言

近年来，致密油藏成为全球能源勘探开发的热点之一[1]。致密油藏一般孔隙度小于10%，基质覆压渗透率小于0.1×10-3μm2，以纳米级孔喉连通体系为主[2]。人们研究发现低渗致密储层中启动压力梯度现象广泛存在：THOMAS L K等[3]发现多孔介质中存在启动压力现象；PRADA A等[4]观察盐水通过固结岩心的渗流，发现启动压力梯度现象；ZENG B Q等[5]研究不同组分流体对岩石启动压力梯度的影响；丁景辰等[6]研究致密气藏启动压力梯度，并将启动压力梯度应用在气田开发中；白慧芳等[7]通过实验测得鄂尔多斯盆地致密储层启动压力梯度。

GRINGARTEN A C等[8]首次将Green函数引入石油工程，结合Newmann乘积求解不同类型的油藏渗流问题，推动不稳定试井的发展；OZKAN E等[9]考虑井筒储集系数和表皮因数，以及不同边界条件、不同类型油藏(如均质油藏和裂缝性油藏)等复杂因素，提出Laplace空间变量形式的点源函数。基于Laplace空间源函数方法，UMNUAYPONWIWAT S等[10]研究压裂井中非达西渗流对压力动态的影响，提出若忽略裂缝中的非达西渗流，则导致裂缝导流能力和裂缝半长误差超过50%；ZERZAR A等[11]考虑均匀流量、无限导流和有限导流3种裂缝情况，提出压裂水平井模型；根据Ozkan的点源函数，樊冬艳等[12]研究人工裂缝倾角对压裂水平井压力动态的影响，并将源函数方法扩展到页岩气藏；ZHAO Y L等[13]将源函数引入考虑SRV的复合油藏；REN J J等[14]结合源函数和数值离散方法，研究页岩气藏中有限导流裂缝、不同裂缝分布等复杂情况； REN Z X等[15]应用Ozkan的面源解和叠加原理，研究复杂裂缝网络中水平井不稳定压力特征。多数研究基于达西渗流条件下的源函数，没有考虑致密油藏因启动压力梯度导致的低速非达西渗流[16]。少数研究考虑启动压力梯度的源函数：根据渗流力学基本原理，熊佩[17]建立低渗油藏低速非达西渗流数学模型，以及Lord Kelvin瞬时点源修正解；GUO J J等[18]考虑启动压力梯度影响，推导Laplace空间下的Ozkan修正点源解，沿水平井筒积分得到井底压力；闫星宇等[19]建立低渗油藏直井渗流模型，采用Lord Kelvin瞬时点源修正解、贝塞尔函数积分和泊松叠加公式，对渗流方程沿井筒积分求解井底压力。这些研究对常规点源解和启动压力梯度修正项运用叠加原理，缺乏数学理论支撑，同时放大启动压力梯度的影响。

基于低速非达西渗流，考虑启动压力梯度影响，笔者建立无限大地层点源数学模型，求解Laplace空间下的修正点源解，将其分解为达西项和启动压力梯度修正项。对达西项运用镜像映射和叠加原理得到不同类型的基本解，再附加启动压力梯度修正项，考虑井筒储集系数和表皮因数影响，得到井底压降解。与经典解析解对比，验证模型的正确性。该点源解的叠加方式在数学上严格证明成立，又具有明确的物理意义。应用该模型研究不同类型井的井底压力动态特征，并进行现场应用。

1 修正点源解

假设条件：无限大致密油藏中存在一恒定连续点源，初始状态的储层压力均匀分布；流体及岩石微可压缩，压缩系数为常数；忽略重力影响和地层温度变化。

1.1 数学模型

致密油藏中普遍存在启动压力梯度现象，基于低速非达西渗流规律，运动方程[20]可表示为

(1)

式中：v为渗流速度；K为储层渗透率；μ为流体黏度；p为地层压力；r为任意点到储层中心的径向距离；G为启动压力梯度。

结合运动方程、状态方程和连续性方程，建立考虑启动压力梯度的致密油藏渗流微分方程：

(2)

式中：φ为储层孔隙度；Ct为综合压缩系数；t为时间。

初始条件：

p(r,t)=pi,t=0 h,

(3)

式中：pi为原始地层压力。

内边界条件：

(4)

外边界条件：

p(r,t)=pi,r→∞。

(5)

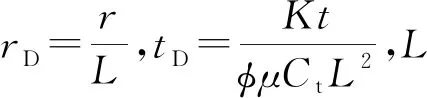
(6)

(7)

(8)

式中：s为Laplace空间变量。

构造式(6)的一个特解：

(9)

将式(9)代入式(6)，可验证式(6)成立，因此构造的特解正确。

式(6)对应的齐次方程为

(10)

其通解为

(11)

式中：A和B为待定常数。

式(6)的解为

(12)

B=0,

(13)

(14)

考虑启动压力梯度的致密油藏无限大地层修正点源解为

(15)

式中：dD为地层中任意一点(xD，yD，zD)到点源(xwD，ywD，zwD)的距离。

1.2 分解方法

将修正点源解分为两部分，即任意一点的压降分为两部分，有

(16)

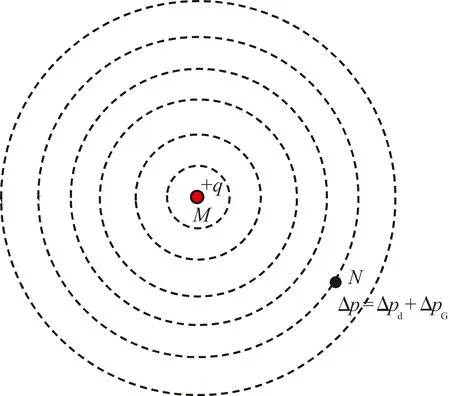
图1 修正点源解分解示意

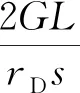
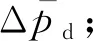
2 不同井型井底压降解

由修正点源解分解可知，地层中任意一点的压降为源汇项在该点产生的压降和启动压力梯度引起的附加压降的总和。对于不同井型的井底压降由两部分组成：第一部分为不同井型的源汇项叠加在井底产生的压降；第二部分为启动压力梯度项引起的附加压降。由于启动压力梯度引起的附加压降与边界无关，设定致密油藏边界为顶底封闭、四周无限大，同时考虑井筒储集系数和表皮因数影响，研究不同井型的井底压降解。

2.1 源汇项叠加压降解

以致密油藏垂直井为例，基于镜像映射和叠加原理消除边界影响，再沿垂直井筒积分得到达西渗流情况下的井底压力。

无限大地层修正点源解的达西项为

PPP投资型项目投资管理中，要深入施工现场调查，详细掌握项目工程建设基本情况。然后制定健全的投资管理制度，明确管理目标和要求，推动投资管理活动顺利进行。要制定合理的投资预算，对资金使用作出科学安排，防止资金浪费现象发生。要提高施工图纸设计水平，加强图纸审核，对存在的问题及时采取优化措施，从而有效指导PPP投资型项目建设，防止延误工期。要明确施工的重点环节，对施工现场拍照，加强现场清单管理，保证现场秩序良好，施工资金得到合理利用[3]。总之，从多个方面入手，提升投资管理水平，有利于促进项目效益提升。

(17)

应用镜像映射消除顶底边界的影响，根据叠加原理和Poisson公式[9]化简式(17)，得到顶底封闭边界的点源解为

(18)

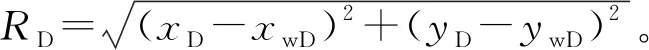
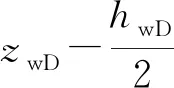
(19)

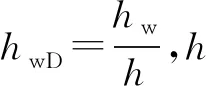
2.2 启动压力梯度附加压降解

(20)

由式(20)可知，任意一点N的附加压降与该点的启动压力梯度和到源(点、线、面)的距离有关。不同源类型启动压力梯度修正项中距离的表达形式见表1。

2.3 井底压降解

由表1可知，在完全穿透直井模型中dD=rD，致密油藏垂直井的压降解为

(21)

同理，可推导顶底封闭、四周无限大致密油藏其他井型的基本解，不同井型的致密油藏井底压降解见表2。

在Laplace空间利用Duhamel原理[21]，引入量纲一的井筒储集系数CD和总表皮因数St，考虑井筒储集系数和总表皮因数，得到Laplace空间下的井底压力为

(22)

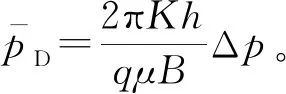
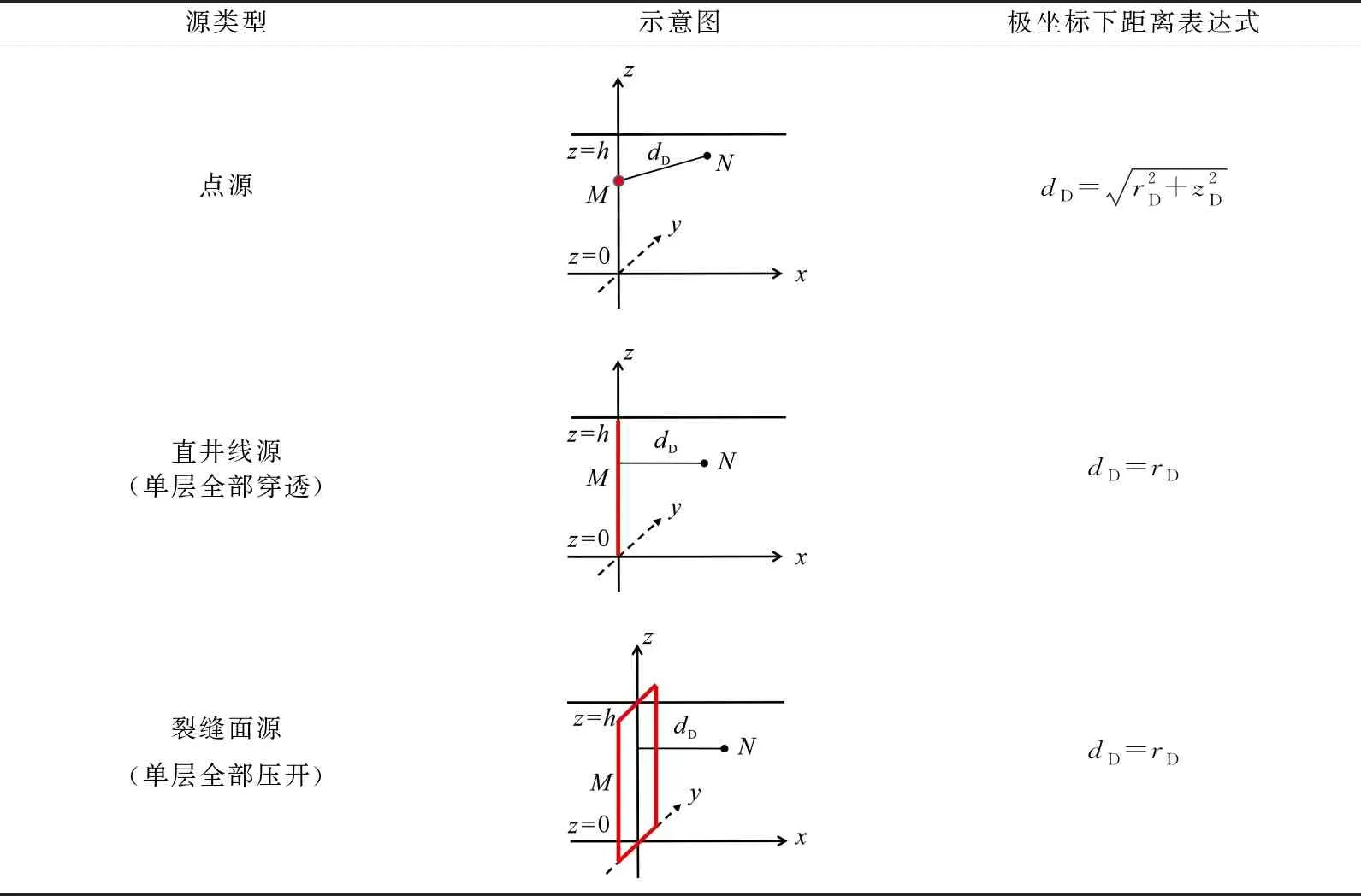
表1 不同源类型启动压力梯度修正项中距离的表达形式

表2 不同井型的致密油藏井底压降解

根据Stehfest数值反演[22]得到真实空间的井底压降解为

(23)

(24)

式(23)的精度主要取决于vi，vi由N确定：

(25)

pwD(tD)对N很敏感，N采用试凑法确定，一般取4～18的偶数。

3 结果讨论

3.1 模型验证

3.1.1 经典解析解

为了验证文中方法的正确性，以顶底封闭、四周无限大致密油藏中完全穿透直井为例，直井全部穿透的均质地层可简化为平面径向流动。致密砂岩储层岩心启动压力梯度为0.001～0.100 MPa/m[6-7]，因此选择启动压力梯度为0.010 MPa/m。数值模拟计算参数见表3。

表3 数值模拟计算参数

将文中方法求得的井底压降解与低速非达西渗流条件下的井底压降解进行对比，经典解析解[23]为

(26)

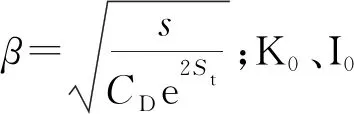
不同启动压力梯度下直井的压力动态特征见图2。由图2可知，运用文中方法得到的试井模型与经典解析解吻合良好，验证文中方法的正确性。致密油藏垂直井的流动阶段主要分为井筒储集和径向流阶段。不考虑启动压力梯度时(G=0 MPa/m)，径向流阶段压力导数为0.5的水平线；考虑启动压力梯度时，压力及压力导数曲线在径向流阶段后期出现一定程度的上翘，说明致密油藏需要消耗更多的能量。随启动压力梯度增加，径向流阶段的曲线发生上翘时间提前且上翘幅度增大。

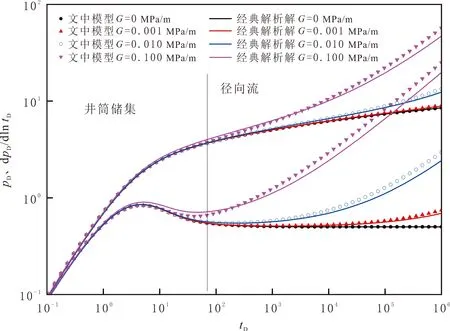
图2 不同启动压力梯度下直井压力动态曲线

3.1.2 其他模型

与其他模型进行对比，将文中方法记为方法1，熊佩[17]对点源项和启动压力附加项进行叠加的方法记为方法2，GUO J J等[18]、CAO R Y等[24]应用点源函数叠加的方法分别记为方法3和方法4，在顶底封闭、径向无限大的低渗油藏中，不同叠加方式的直井井底压力表达式见表4。

表4 不同叠加方式的直井井底压力表达式

令CD=1、S=2，其他参数见表3，分别计算启动压力梯度为0、0.001、0.010、0.100 MPa/m时，不同叠加方式试井模型的井底压力动态曲线见图3。由图3可知，存在启动压力梯度时，方法2、3、4计算得到的井底压力和压力导数远比方法1的结果大。方法2、3、4在求解直井井底压力时，对无限大地层点源解的达西项和启动压力梯度修正项进行叠加，增大启动压力梯度的影响；文中方法只对达西项进行叠加，再修正启动压力梯度引起的附加压降，比其他模型的叠加方式更合理。

3.2 不稳定压力动态分析

应用修正点源函数方法，仿照直井不稳定压力的求解过程，假设地层顶底封闭、四周无限大，分析致密油藏压裂直井、水平井及压裂水平井的井底压力动态。

3.2.1 压裂直井

裂缝半长Lf=50 m，产油量q=50 m3/d，量纲一的井筒储集系数CD=0.005，其他参数见表3。不同启动压力梯度的致密油藏压裂直井的压力动态曲线见图4。由图4可知，致密油藏压裂直井主要分为3个流动阶段：井筒储集、裂缝线性流和系统拟径向流阶段。启动压力梯度主要影响曲线中后期，考虑启动压力梯度后，压力及压力导数曲线上翘，启动压力梯度越大，上翘越早，上翘程度越大。

3.2.2 水平井

水平井长度Lh=1 000 m，地层渗透率K=0.05×10-3μm2，量纲一的地层厚度hD=0.25，日产量q=50 m3/d，量纲一的井筒储集系数CD=2.5×10-4，其他参数见表3。不同启动压力梯度的致密油藏水平井的压力动态曲线见图5。由图5可知，致密油藏水平井主要分为4个流动阶段：井筒储集、早期径向流、地层线性流和系统拟径向流(晚期径向流)阶段。启动压力梯度主要影响曲线的中后期，影响情况与压裂直井的类似。

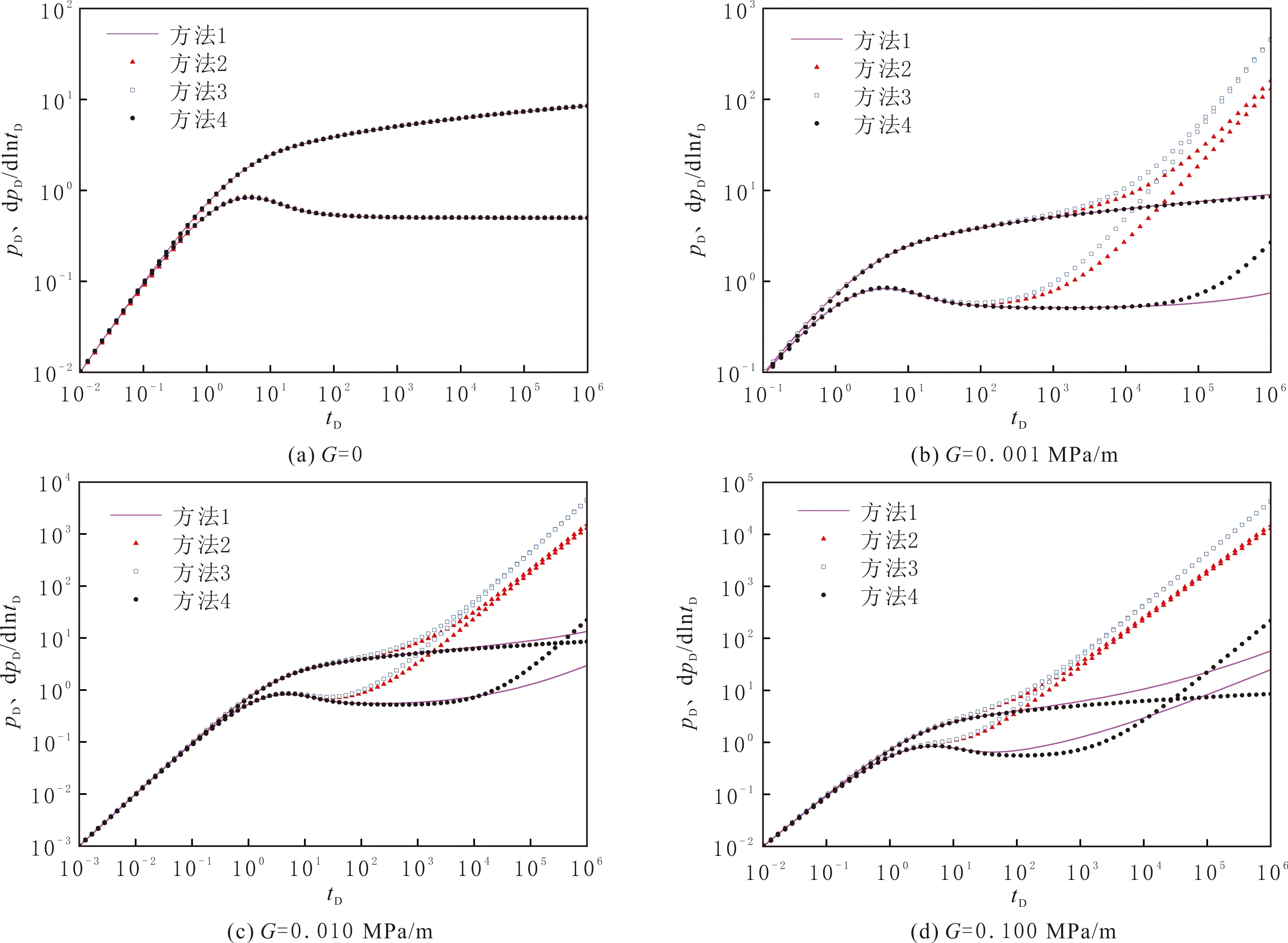
图3 不同叠加方式试井模型的井底压力动态曲线

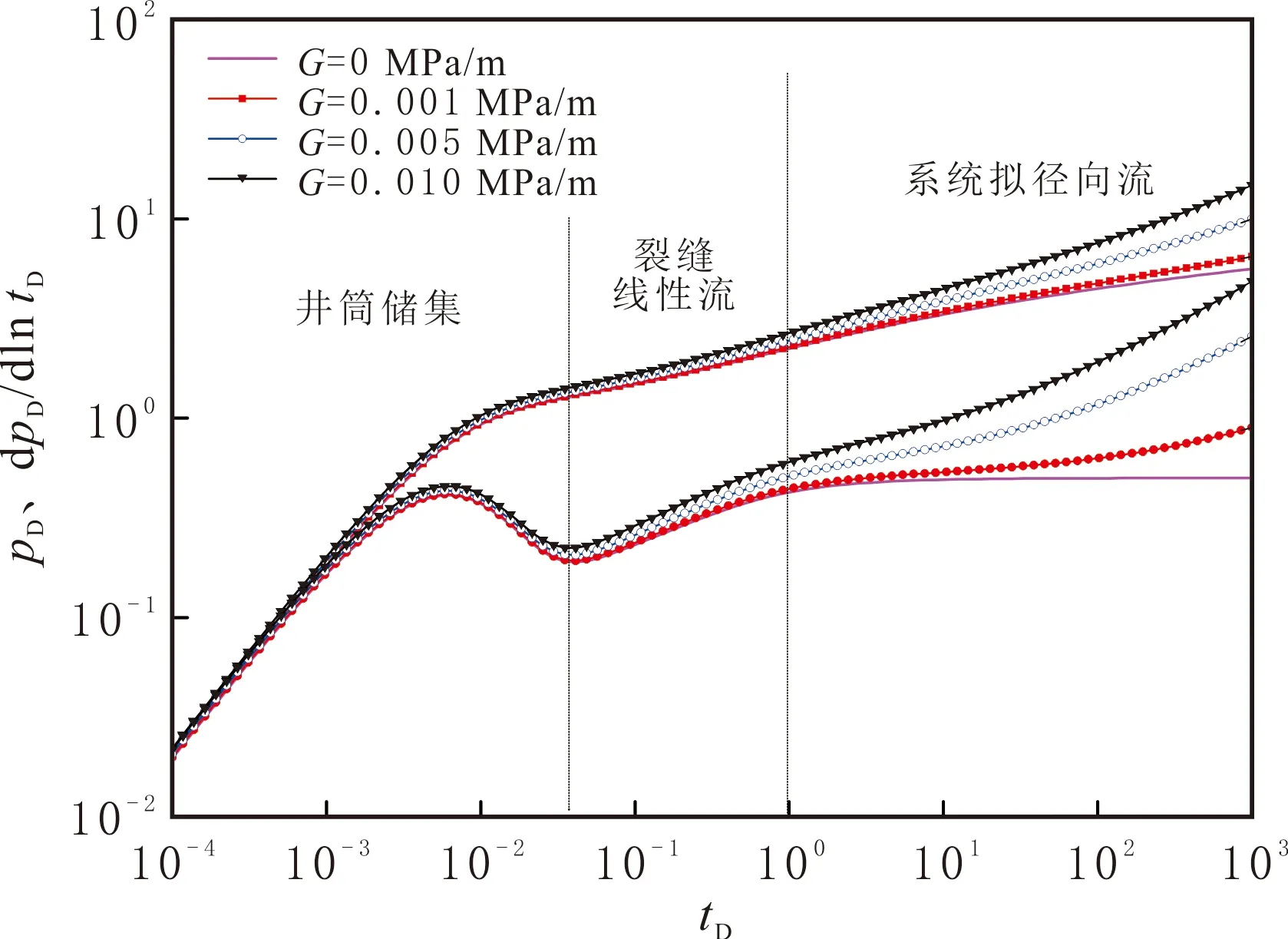
图4 不同启动压力梯度的致密油藏压裂直井压力动态曲线

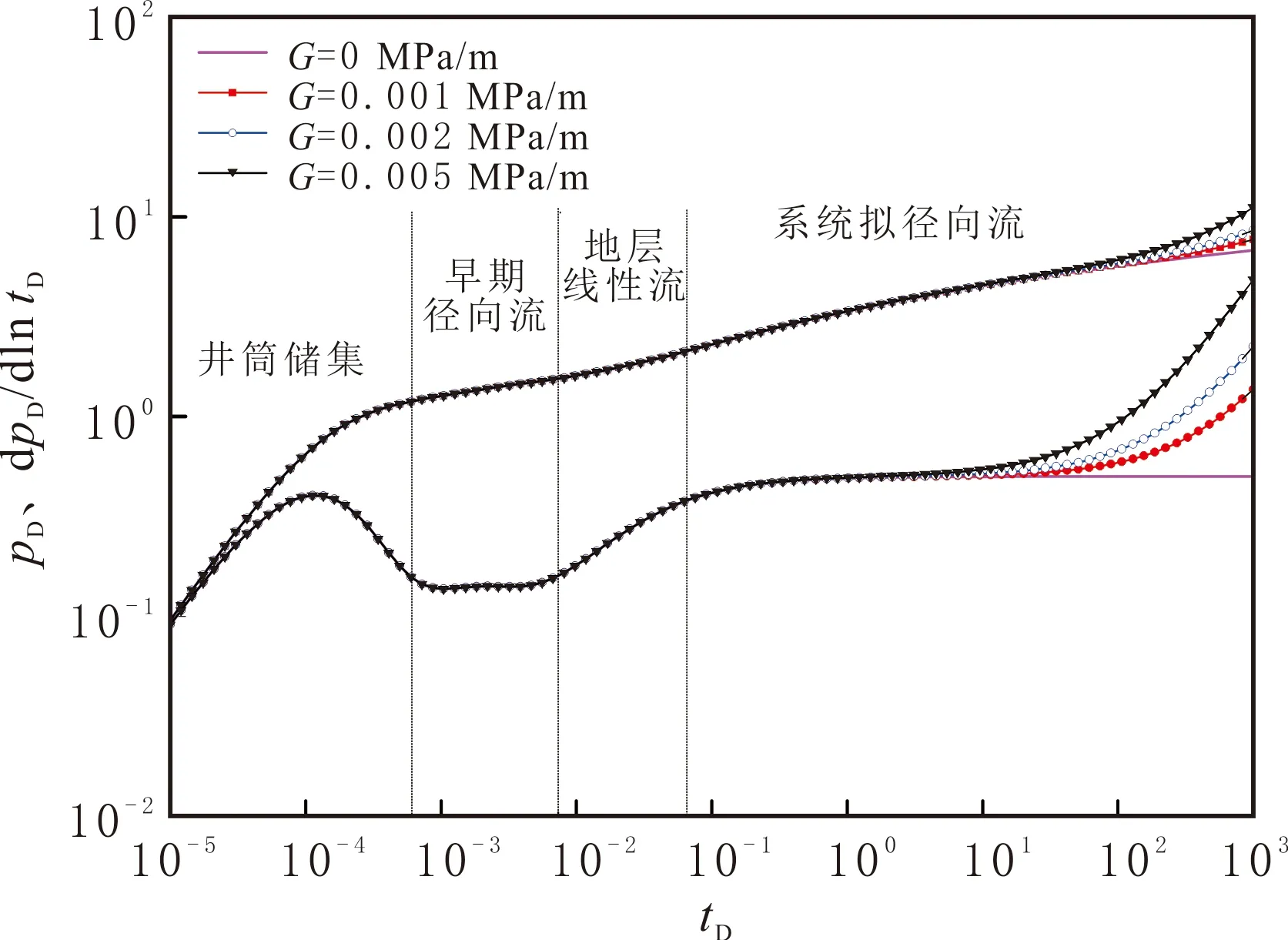
图5 不同启动压力梯度的致密油藏水平井压力动态曲线

3.2.3 压裂水平井

水平井长度Lh=500 m，地层渗透率K=0.05×10-3μm2，地层厚度h=20 m，产油量q=10 m3/d，3条水力压裂裂缝半长Lf=50 m，裂缝间距150 m，量纲一的井筒储集系数CD=1.0×10-4，表皮因数St=0.3，其他参数见表3。不同启动压力梯度的致密油藏压裂水平井的压力动态曲线见图6。由图6可知，压裂水平井主要分为4个流动阶段：井筒储集、裂缝线性流(第一线性流)、地层线性流(第二线性流)和系统拟径向流阶段。实际裂缝间距较小，裂缝之间干扰严重，通常难以观察到裂缝周围的流体近似径向流向裂缝(裂缝径向流)。启动压力梯度主要影响地层径向流阶段，启动压力梯度越大，曲线上翘程度越明显。

4 矿场应用

以鄂尔多斯盆地某区块的一口压裂水平井——JP1井为例。JP1完钻井深3 408.90 m，水平段深度为2 776.60～3 401.60 m，水平井长度为625 m，射孔井段为2 803.00～2 805.00、3 069.00～3 071.00、3 364.00～3 366.00 m，射开厚度为6.0 m，射孔处3段压裂。关井前，日产油量为10 m3，JP1井基本参数见表5。

表5 JP1井基本参数

采用自适应遗传算法编制软件实现自动拟合，遗传算法流程：(1)确定量纲一的水平段长度、裂缝半长、裂缝条数和裂缝导流能力等参数的优化范围，随机生成N个二进制编码，位数由各参数的精度和范围决定，即随机生成初始种群的N个个体；(2)分别对每个个体进行解码，得到各参数并代入压裂水平井井底压降解，进而得到各个体对应的适应度，即实测压力与理论压力的误差平方和；(3)根据各个体适应度大小，利用“轮盘赌”模型进行选择操作，并利用个体的交叉概率和变异概率进行交叉和变异操作，得到下一代种群的新个体；(4)判断是否达到优化次数，若已达到，则停止迭代并输出该种群的平均适应度和最大适应度；否则返回步骤(2)继续优化。

将实测数据点导入编制软件，画出实测试井压力动态曲线，考虑启动压力梯度影响，选择盒状封闭的致密油藏压裂水平井模型，应用软件实现自动拟合，拟合结果见图7，理论曲线与实测曲线拟合较好，验证采用文中方法得到的试井解释模型正确，拟合得到试井解释参数见表6。

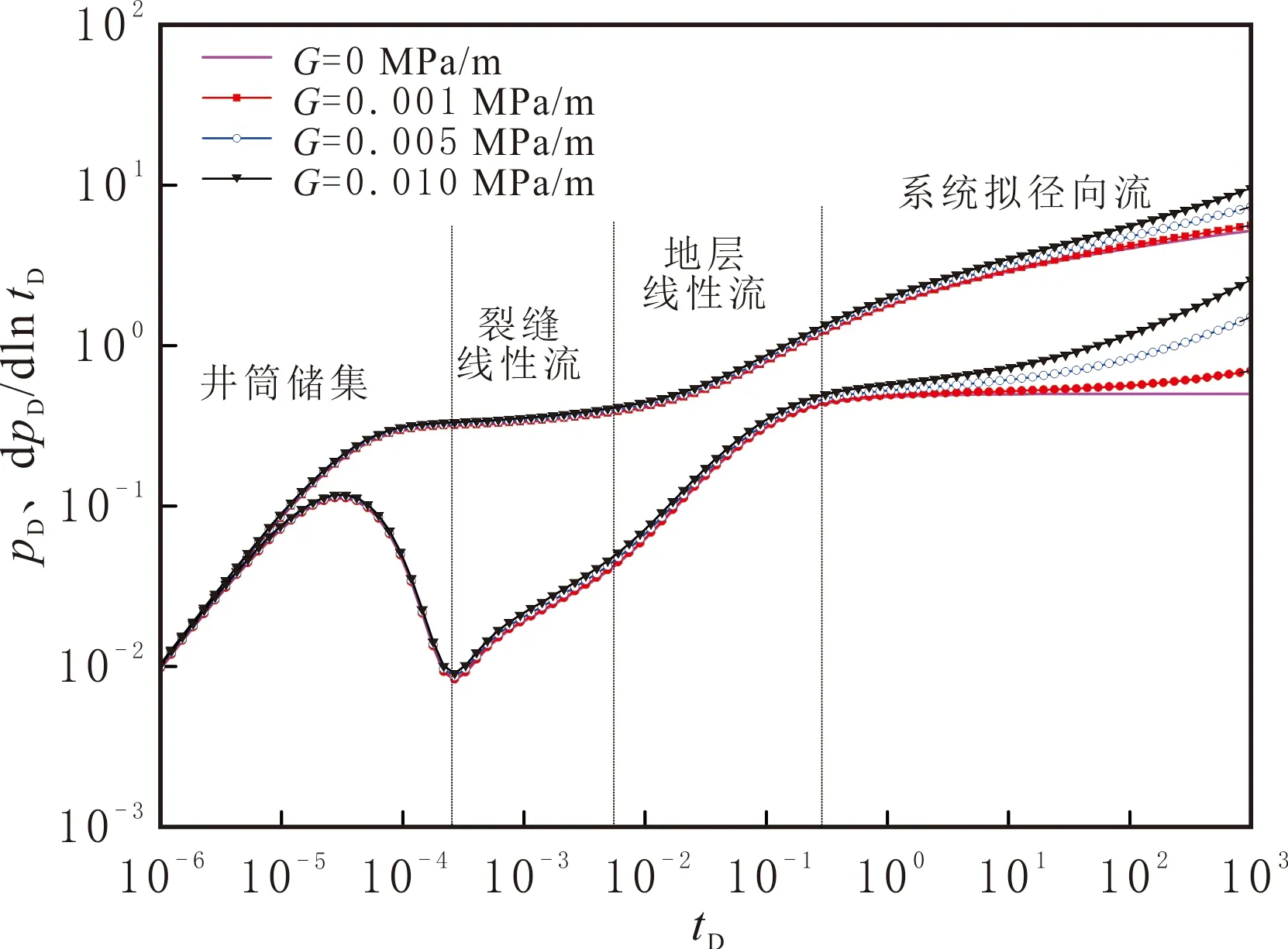
图6 不同启动压力梯度的致密油藏压裂水平井压力动态曲线

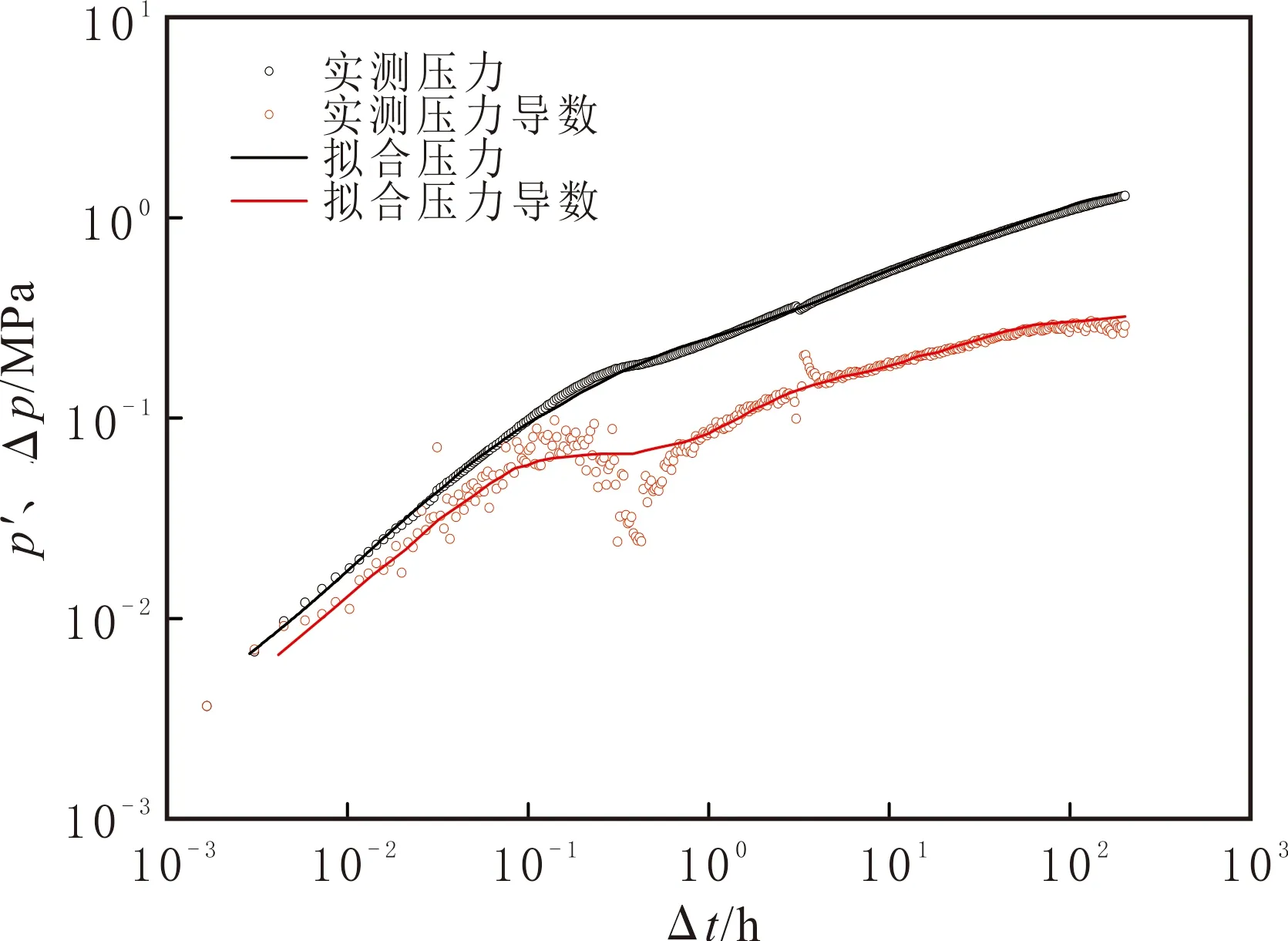
图7 JP1井试井数据拟合结果

5 结论

(1)基于非达西渗流，提出考虑启动压力梯度的致密油藏不稳定试井解析方法。建立无限大地层点源数学模型，求解Laplace空间下的修正点源解；分解点源解为达西项和启动压力梯度修正项，运用镜像映射和叠加原理，附加启动压力梯度修正项；考虑井筒储集系数和表皮因数影响，得到井底压降解。

(2)对比经典解析解验证模型正确性，仅对达西项运用叠加原理的处理方式更加合理，既在数学上能够严格证明成立，又具有明确的物理意义。

(3)不同井型的启动压力梯度主要影响压力动态曲线的中后期，压力及压力导数曲线后期出现不同程度的上翘。致密油藏中需要更多的能量消耗，在致密油藏实际开发过程中，应注意合理配产，防止地层压力消耗过快。