基于比特平面分解的图像加密算法
2021-05-20熊继伟吴秋新
熊继伟,吴秋新
(北京信息科技大学 理学院,北京 100192)
0 引言
不同于文本数据,数字图像作为一种二维数据,其数据量大,冗余度高,像素间相关性强。传统的加密方法如高级加密标准(advanced encryption standard,AES)、数据加密标准(data encryption standard, DES)、RSA加密算法(Rivest, Shamir, Adleman)、国际数据加密算法(international data encryption algorithm, IDEA)等并不适合用来加密图像[1-2]。目前,数字图像加密算法按加密思路主要分为以下几类:基于空间域的像素置乱、基于混沌的加密、基于变换域的加密。陈关荣等[3]提出了像素置乱和异或扩散的加密算法,但由于此算法产生的混沌序列与明文无关联,导致加密算法可以被选择明文攻击破译。邓晓衡等在文献[3]的基础上提出比特置乱加密算法[4-8],既保留了原算法的优点,又通过比特置乱进一步改变像素值,更好地隐藏明文统计特征,同时将混沌序列与明文产生关联,使得中间密钥随明文自适应变化,能较为有效地抵御选择明文攻击。
本文提出一种新的加密算法,能够分别对不同的比特平面使用不同的置乱方式,可以有效地破坏明文的相关性,更好地隐藏明文的信息。同时密钥和明文有很强的相关性,能够抵抗文献[9]所提出的攻击方法。
1 算法基础
1.1 混沌系统
混沌现象是在非线性动力系统中表现的确定性、类随机的过程,这种过程既非周期又不收敛,并且对于初始值具有敏感依赖性。这种现象很契合加密算法需要的伪随机序列的特性。
logistic映射[10]是一种简单快速、易于实现的混沌映射。其表达式为
x(n+1)=μxn(1-xn)
(1)
当参数xn∈(0,1),μ∈(3.57,4]时,logistics映射处于混沌状态,如图1所示。

图1 混沌系统
1.2 比特置乱
由于每个图像由8个比特平面组成,不同比特平面所占权重不同,所以包含的信息也有所差异,每个比特平面所包含的信息为
(2)
由式(2)可以看出,从I1到I8图像所包含的信息逐渐增多。为了提高加密算法的抗攻击性,首先对比特平面进行归一化,使用比特循环右移打乱每个平面的信息分布。归一化之后每个平面信息分布能够更加平均。
2 加密算法流程
本文提出的加密算法流程主要由以下几部分组成:1)密钥及混沌序列的生成;2)比特循环位移及分平面置乱;3)组合比特平面。
加密步骤如图2所示。首先计算出明文图像的SHA-256值,该散列值是一个具有256 bit的值,用一个长度为64位的16进制字符串表示。尽管两幅图像之间仅有任意一个bit的区别,但产生的散列值截然不同[11-12]。将明文图像的散列值与密钥进行异或计算,通过logistic映射产生混沌序列用于比特循环位移与比特平面置乱。最后组合比特平面得到密文。解密算法是加密算法的逆过程。

图2 加密算法流程
2.1 初始值的计算
步骤1读取明文图像P(m×n),其中m,n分别为图像P的长和宽。计算明文图像的SHA-256值与密钥异或计算结果H={H1,H2,…,H64}。
步骤2由式(3)~(6)计算出logistic映射初始值x0,参数μ,以及弃置项个数c。
(3)
(4)
(5)
(6)
2.2 随机序列生成
将式(4)和式(5)产生的初始值代入式(1)迭代c+9×m×n次,得到长度为c+9×m×n的随机序列,弃置前c项以保证序列的随机性,然后将迭代得到的随机序列按顺序分为9段,得到一组随机序列t0,t1,t2,…,t8,其中每个序列的长度为m×n。
2.3 比特循环位移
取随机序列t0,将原图像P中的所有像素灰度值pi按照式(7)映射产生新的图像。

(7)
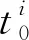

(8)
将比特循环位移后的图像R的每个像素的灰度值按照式 (9)分解成为8个比特平面,得到8个分解之后的比特平面R1~R8:
(9)
式中:R为循环位移之后的图像;Ri为第i个比特平面。
对图像进行比特循环位移能够使每个比特平面包含相近的信息量。从图3和图4可以看出,经过比特循环位移之后的每个比特平面所包含的信息量大致相同,而未循环位移分解的比特平面的信息较多地集中于高比特平面。

图3 未循环位移的8个比特平面

图4 循环位移之后的8个比特平面
2.4 比特平面置乱
取随机序列t1~t8按照算法1产生置乱序列v1~v8。将上节分解得到的8个比特平面R1~R8与置乱序列v1~v8应用算法2置乱。
算法1生成置乱序列

输入: 随机序列t输出: 置乱序列v1: l = length of t2: w = 1,2,3,4,…,l3: for i = l,…,4,3,2,1 Do4: 交换wi,wmod(ti,i-1) 5: end for
算法2置乱

输出:置乱序列v, 图像矩阵R输入:置乱图像矩阵R'1: l = length of v2: for i = 1,2,3,…,l Do3: R'i=Rvi4: end for
2.5 合并比特平面
最终密文图像为合并置乱之后的8个比特平面:
(10)
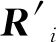
3 仿真结果与分析
选择lena图像,在Python3.6环境下对本文提出的算法进行实验仿真,加密与解密效果如图5 所示。

图5 加密与解密效果
由图可见,使用本文提出的算法进行加密,密文完全隐藏明文图像信息。下面从统计特征、信息熵、密钥敏感性、明文敏感性、密钥空间这几个角度进行分析对比。
3.1 统计特征分析
3.3.1 直方图分析
对图像P中每个像素pi的灰度值进行统计,得出图像灰度值的分布情况如图6所示。
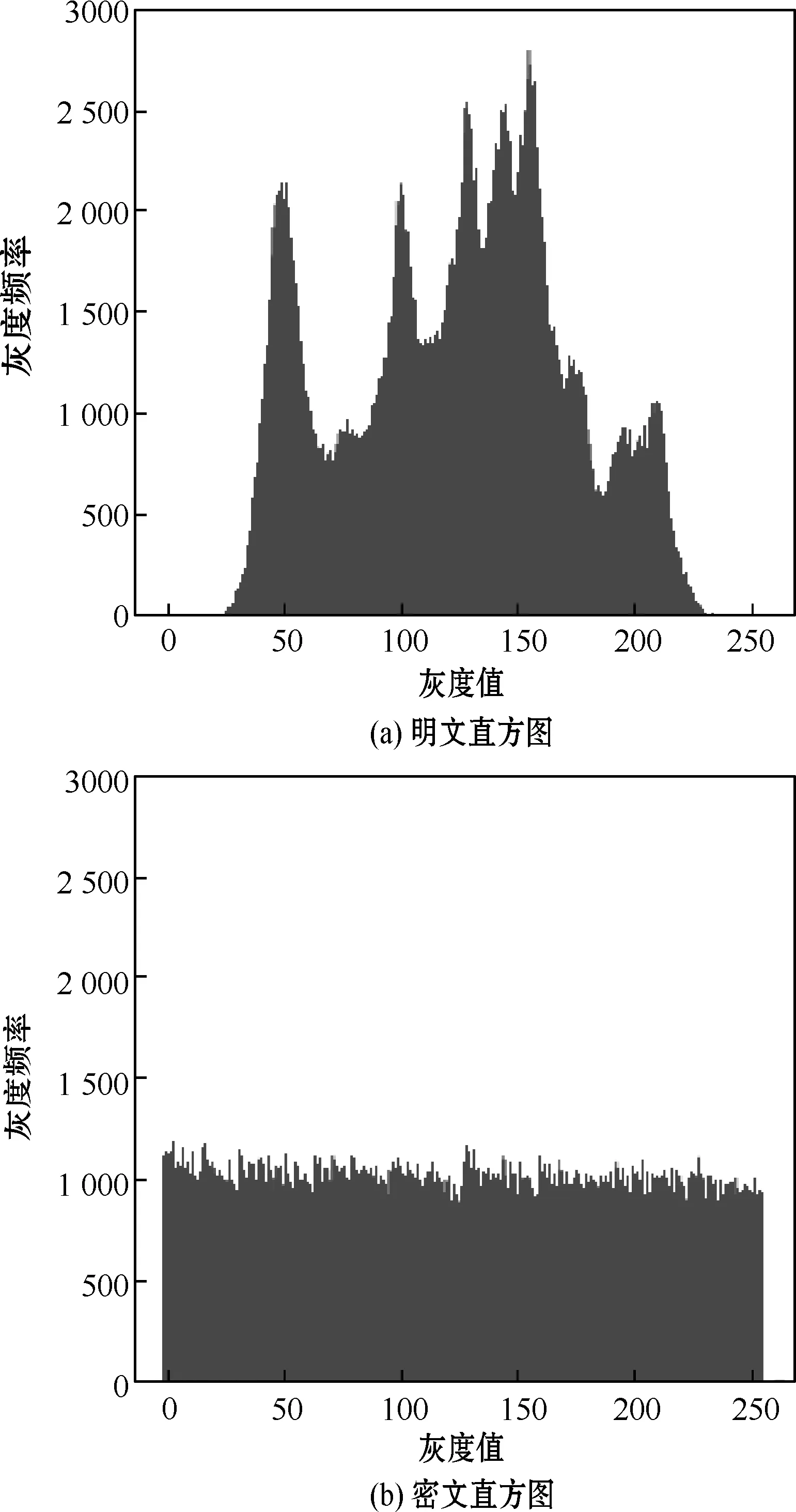
图6 直方图统计
由图6可以看出,明文图像的灰度值有明显的分布规律。而经过加密的密文图像的直方图各个灰度值分布得非常均匀,很好地隐藏了明文图像的信息,使得攻击者难以通过灰度值分布得到信息。
3.3.2 相邻像素相关性
对于一个安全的图像加密算法,应该能够明显地破坏明文图像相邻像素的相关性。
图7 显示了对随机抽取的500个像素点的明文水平相邻像素和密文水平相邻像素的相关性。
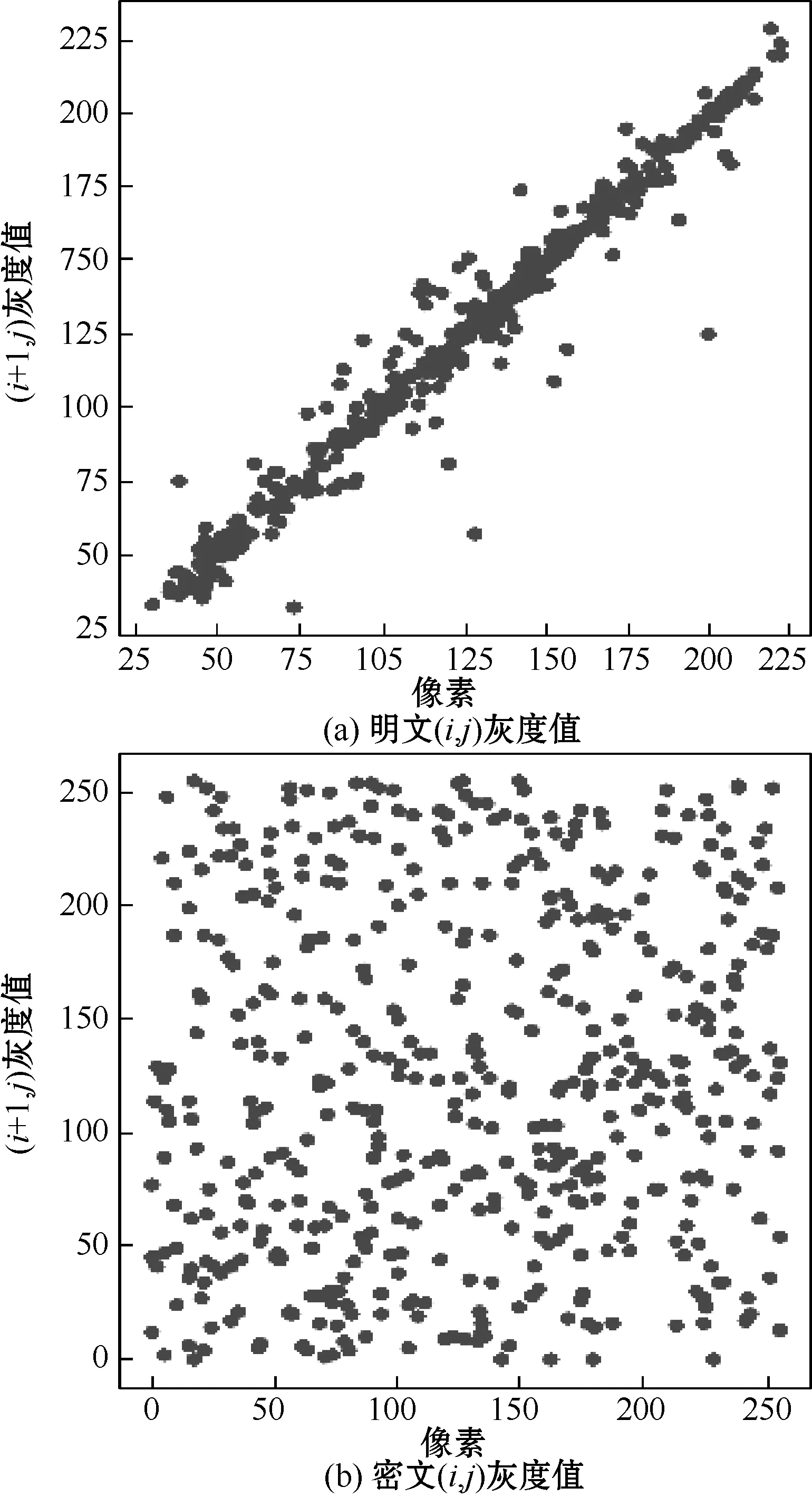
图7 水平相邻像素相关性
由图7可以看出,明文图像的相邻像素有很强的相关性,这是由图像的特点决定的,任何一个有意义的图像,其相邻像素必然有很强的相关性。对于加密之后的图像,其相邻像素的相关性明显降低。由此可见,本文提出的加密算法能够很好地破坏图像相邻像素的相关性,有较高的安全性。
3.3.3 信息熵
信息熵[13]为
(11)
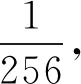
3.2 密钥敏感性分析
密钥敏感性是指解密算法接收到的错误密钥不管与正确密钥多接近都无法正确解密出明文的属性。本文提出的算法在错误密钥与正确密钥仅仅有一位不同时,解密出的明文如图8所示。可以看出,本文提出的算法对密钥有非常高的敏感性。

图8 密钥解密效果
3.3 明文敏感性
明文敏感性是指加密过程中不管两个明文有多接近,加密之后得到的密文也存在差距的属性。
本文采用灰度值变化率RNPC作为指标来分析明文敏感性。原图像加密之后明文为C1,随机交换原图像中两个像素点的位置进行加密之后得到的密文为C2。灰度值变化率为
(12)
式中M、N分别为图像的长与宽。当C1(i,j)=C2(i,j)时p(i,j)=0,否则p(i,j)=1。本文算法灰度值变化率为0.996,对比文献[4]的0.634和文献[5]的0.633,本文算法对于明文敏感性更高。
3.4 密钥空间
本文提出的加密算法使用了3个参数,长度分别为64,50,14。任意一个参数错误都将无法解密密文。因此密钥空间大小为2128。从安全角度来讲,密钥空间大于2100就具有较高的安全性[14],可知本算法能够抵抗一般的穷举攻击。
4 结束语
本文提出了一种新的图像加密算法,能够处理任意大小的图片,并且拥有较高的性能,对于常见的攻击方式具有较好的抵抗能力。采用的分解比特平面的方法不仅能够增加加密系统的安全性,同时也能够提高加密解密的性能,增强了算法的实用性。实验结果表明,本文提出的加密算法对密钥十分敏感,符合加密算法的要求。如何扩大密钥空间使得加密算法更加安全是我们今后研究的重点。
