不同坡率的胶凝砂砾石高坝应力与位移分析
2018-09-10杨冬升吴艾儒罗远吕坤曾文丽潘美言黄雯卢子祥
杨冬升 吴艾儒 罗远 吕坤 曾文丽 潘美言 黄雯 卢子祥

摘要:选择高120m的胶凝砂砾石坝进行不同坡率的坝体应力与位移分析。在建模时使用节点耦合技术,解决了ANSYS有限元模型不同材料分区公共边界材料属性划分、坝基扬压力施加问题。应力分析表明:第一主应力最大值、剪切应力最大值和最小值有相同变化趋势,即均在坡率m=0.8时取得最大值,在m=0.75时取得最小值。位移分析表明:按位移绝对值从大到小排序,依次对应坡率0.80、0.65、0.70、0.60、0.75。综合考虑,建议优选坡率m=0.75。
关键词:胶凝砂砾石;高坝;坡率;应力:位移
中图分类号:TV314
文献标志码:A
doi: 10.3969/j.issn.1000-1379.2018.04.024
胶凝砂砾石坝(Cement-Sand-Gravel Dam,简称CSG坝)所用筑坝材料是坝基、山体、天然河床开挖废弃料等,具有造价低、地基适应性强、抗震性能高、低碳环保等优点。国外最高的胶凝砂砾石坝是土耳其的Cindere坝(坝高为107m),其余坝高均在40m以下;国内永久性胶凝砂砾石坝只有在建的山西守口堡坝(坝高为60.6m),其余均为胶凝砂礫石围堰(临时性水工建筑物)。
经优化计算,参考国内外已建的胶凝砂砾石坝断面形状,胶凝砂砾石坝坝体断面多为梯形。梯形坝坡的坡率是影响工程量、坝体内部应力与位移的关键因素。可以参考的已建胶凝砂砾石高坝很少,其是否可以选择更小的坝坡,需要通过试验研究、模拟仿真进行分析。
本文选择坝高为120.0m的胶凝砂砾石坝进行有限元参数化建模,计算了不同坡率胶凝砂砾石坝体的应力、位移,给出优选的坝坡坡率。
1 胶凝砂砾石高坝有限元模型
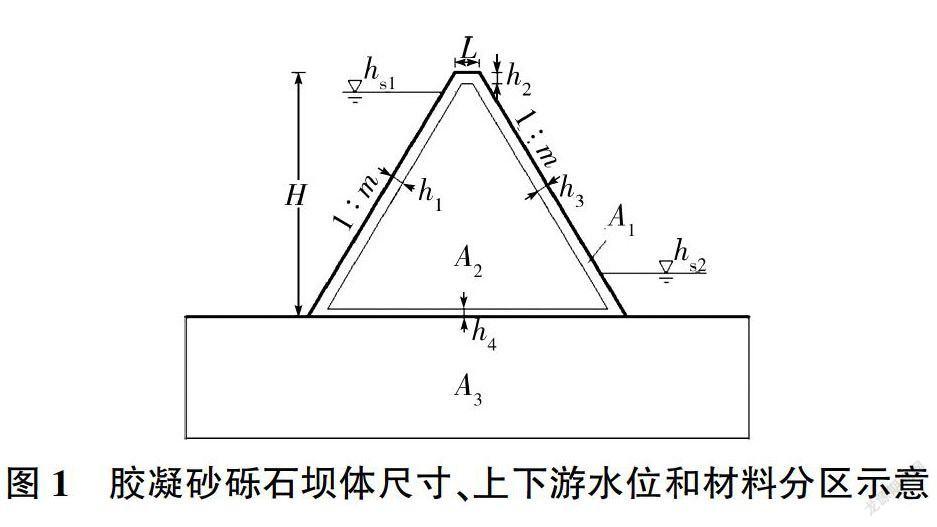
胶凝砂砾石坝的坝体尺寸、上下游水位、材料分区示意见图1。图1中:H为坝体高度,L为坝顶宽度,m为坡率,hsl为上游水位,hs2为下游水位。胶凝砂砾石坝体防渗多为“金包银”方式,即坝体周边用常态混凝土防渗,其厚度上游为h1、坝顶为h2、下游为h3、坝底为h4。胶凝砂砾石坝体有限元模型共3个分区:A1为外部常态混凝土防渗层,A2为内部胶凝砂砾石胶结材料主体,A3为坝基。
对胶凝砂砾石高坝使用ANSYS有限元软件APDL参数化建模,具体过程如下:用参数化命令流K生成关键点、L连接关键点、AL生成胶凝砂砾石坝3个分区、AATT赋予分区属性、AMESH划分网格、CPINTF(CPINTF,ALL,0.0001,)实现分区公共边界的节点耦合、DL定义约束线、SFL施加水压力、ACEL施加惯性力、SOLVE求解。
参考守口堡胶凝砂砾石坝、土耳其Cindere胶凝砂砾石坝的坝体尺寸,设本文胶凝砂砾石高坝H=120m、L=12m、h1=h2=6m、h3=5m、h4=3m、hs1=118m、hs2=IOffl。坝体及坝基材料属性见表1。
坝基有限元模型的长、宽分别向上下游、坝基深度取2H。
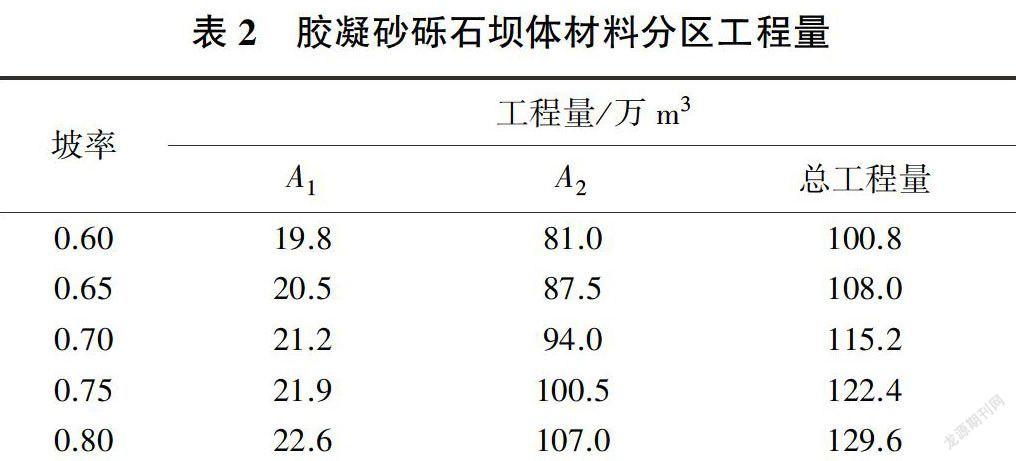
守口堡胶凝砂砾石坝坡率m=0.6、土耳其Cindere胶凝砂砾石坝坡率m=0.7。这里为了探索百米级(坝高在100~200m之间)胶凝砂砾石坝的坡率与坝体应力、位移之间的关系,m分别取0.60、0.65、0.70、0.75、0.80,进行建模分析。假设坝轴线的长度为100m,不同坡率对应的材料分区A1、A2工程量见表2。
由表2可看出相邻坡率之间A,工程量相差0.7万m3、A2工程量相差6.5万m3,坝体总工程量相差7.2万m3。
胶凝砂砾石坝有限元模型如图2所示(以坡率m=0.6为例),x轴以水平向有为正、y轴以竖直向上为正。图2中黄线为胶结材料A2分区与胶凝砂砾石坝体常态混凝土A1分区、胶凝砂砾石坝体常态混凝土A1分区与坝基A3分区存在公共边界上节点耦合后的结果,解决了材料分区公共边界材料属性划分、坝基扬压力施加的问题。由于节点总数是计算自由度的体现,因此表3给出了不同坡率的ANSYS有限元模型节点信息。
2 应力分析
表4给出了不同坡率胶凝砂砾石坝有限元模型计算得到的第一主应力和剪切应力的最大、最小值(σmax、σmin及Tmax、Tmin,应力以压为正、拉为负)。可以看出,A1、A2材料分区中σmax、及Tmax、Tmin有相同变化趋势,即均在坡率m=0.8时取得最大值,在m=0.75时取得最小值。A1、A2材料分区中σmin在坡率m=0.70时取得最大值(绝对值),m=0.75时取得最小值。A1、A2,材料分区中第一主应力和剪切应力最大、最小值随着坡率m的增大或减少并不是线性关系。经比较可知:当坡率m=0.75时,应力最小;当坡率m=0.60时,应力稍小;当坡率m=0.70、0.65、0.80时,应力依次增大。在满足剪切应力的要求下,选择坡率m=0.6,工程量最小。《胶结颗粒料筑坝技术导则》规定最小胶凝砂砾石抗压强度为4.0MPa,因此坡率m=0.65、0.80不满足行业标准要求。胶凝砂砾石材料本体的抗剪强度在0.89~1.44MPa之间,而胶凝砂砾石材料层间抗剪强度在0.43~0.86MPa之间,因此坡率m=0.60、0.70不满足规范要求。故综合考虑,应优先选择坡率m=0.75。
第一主应力云图见图3。可以看出:m=0.60、0.70、0.75时坝体应力分布较均匀;m=0.65、0.80时坝体应力靠近上游部分出现拉应力区,且范围较大:m=0.75时坝体断面仅在下游坝趾处出现很小的拉应力区。
3 位移分析
表5给出了不同坡率胶凝砂砾石坝有限元模型x向最大位移、y向最大位移、xy平面最大位移。按位移绝对值从大到小排序,依次对应坡率m=0.80、0.65、0.70、0.60、0.75,《胶结颗粒料筑坝技术导则》并未给出变形限值,考虑最优的坡率m=0.75。根据不同坡率的x向位移云图可以看出,坝体位移分布有明显的梯度变化。
4 结论
对坝高为120m的胶凝砂砾石坝进行有限元参数化建模,计算了不同坝坡材料分区的工程量,第一主应力和剪切应力的最大值与最小值,x向、y向、x平面最大位移,得到如下结论:
(1)使用节点耦合技术,解决了ANSYS有限元建模不同材料分区公共边界材料属性划分问题、坝基扬压力施加的难题。
(2)相邻坝坡坡率(m差值为0.5)之间外围防渗常态混凝土工程量相差0.7万m3、内部胶结材料工程量相差6.5万m3,坝体工程总量相差7.2万m3。
(3)第一主应力的最大值和剪切应力的最大值、最小值有相同的变化趋势,即均在m=0.8时取得最大值,在m=0.75时取得最小值,因此优选坡率m=0.75。
(4)按位移绝对值从大到小排序,依次对应坡率m=0.80、0.65、0.70、0.60、0.75。综合考虑,建议优选m=0.75。
