超声速气流中液体横向射流雾化过程数值模拟

翟小飞, 白菡尘, 李 春

(中国空气动力研究与发展中心高超声速冲压发动机技术重点实验室, 四川绵阳 621000)

引 言

当前, 飞行Mach数4～7范围的超燃冲压发动机技术正在深入发展并逐步走向工程化应用. 为了进一步提高发动机性能, 更加深入地对液体碳氢燃料(主要是航空煤油)的超声速雾化过程、 蒸发过程、 燃料/空气混合过程、 点火过程及燃烧过程进行研究并获得规律性的结论, 具有重要的意义. 由于气流在超燃冲压发动机燃烧室中的驻留时间很短(仅为毫秒量级), 因此, 如何实现液体燃料的快速雾化和蒸发对提高发动机性能至关重要, 为此, 国内外学者对超声速气流中液体横向射流的雾化过程开展了大量研究工作[1-4].

Lin等[5-7]对超声速气流中液体射流的雾化开展了较为系统的实验研究, 研究了喷嘴尺寸、 气液动量比、 液体物性、 喷射角度等因素对射流雾化过程的影响, 并采用阴影法和相位Doppler粒子分析仪(phase Doppler particle analyzer, PDPA)测量了液体射流穿透深度, 总结出了穿透深度的经验表达式. 岳连捷等[8]基于Euler-Lagrange体系, 采用RANS方法, 对超声速气流中液体射流的液雾结构及液滴破碎过程进行了仿真计算, 得到了与实验结果吻合较好的射流穿透深度, 此外, 研究揭示了液体射流与气流之间的强烈相互作用: 液滴在进入气流中不久就破碎成很小的子液滴, 受煤油液雾的影响, 气流速度、 温度急剧下降. 李佩波等[9]对来流Mach数为1.94的超声速气流中液体横向射流的气液相互作用过程进行了数值研究, 仿真结果较详细地揭示了液体射流喷雾与气流之间的强烈相互作用过程. 计算给出的射流穿透深度、 液滴Sauter平均直径(Sauter mean diameter, SMD)及液滴速度分布均与实验吻合较好.

在超声速气流液体横向射流雾化数值模拟中, 雾化模型的选择至关重要, 很多学者对此展开了研究. 杨顺华等[10]采用K-H/R-T二次破碎模型对Lin等[7]的水射流实验进行了数值模拟, 计算中利用实验数据对模型中的部分参数进行了修正, 从而获得了更加准确的计算结果, 缺点是其计算中涉及的经验参数难以准确给出. 刘静等[11-12]针对超声速横向气流中雾化的特点, 结合雾化机理和实验测量结果, 对原有的混合雾化模型进行了改进, 并将改进后的计算结果与TAB模型和Reitz波模型的计算结果进行了对比. 结果表明: 改进的混合雾化模型的计算结果与实验测量值符合较好, 更适用于超声速横向气流中燃料雾化的数值模拟. 杨东超等[13]分别采用4 种不同二次破碎模型对超声速横向流作用下射流雾化过程进行了数值模拟, 计算结果表明, TAB模型得到的滴径最小, 其穿透深度也最小, 不适用于超声速条件下的破碎过程; SSD模型计算的滴径尺寸较为均一; WAVE模型与K-H/R-T模型的结果相近; 而K-H/R-T模型得到的穿透深度与实验更为相符. 基于上述研究结果, 本文在开展雾化计算时液滴二次破碎模型采用K-H/R-T模型.

总的来说, 国内外学者已经对超声速气流中液体横向射流的雾化过程进行了较为详细和深入的研究, 研究重点主要是气相与液相之间的相互作用, 液滴破碎过程, 液雾结构, 射流穿透深度, 不同二次破碎模型、 喷嘴尺寸、 气液动量比、 液体物性、 喷射角度等因素对射流雾化过程的影响, 液滴直径分布, 液滴速度分布等等. 对于初始液滴直径、 初始雾化锥角以及是否考虑二次破碎对雾化过程的影响等方面, 研究的很少. 而这些问题又是影响雾化数值模拟结果准确性的重要因素. 鉴于此, 本文从这些角度对超声速气流中液体横向射流的雾化过程开展了进一步的数值模拟研究, 以期获得能够指导雾化数值模拟的规律性结论.

1 计算模型及方法

本文数值模拟对象为Lin等于2004年开展的超声速空气气流中水射流实验[7]. 来流为空气, Mach数为1.94, 总压为206 kPa, 总温为533 K. 射流为水, 水通过直径0.5 mm的圆形喷孔垂直喷入空气中. 射流初始温度为298.15 K, 射流/空气动压比为10, 射流流量为20 g/s, 喷射速度为40 m/s(沿Y轴正向喷射). 计算区域为 600 mm×127 mm×152 mm, 如图1所示.

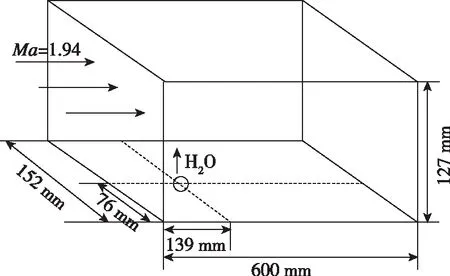
图1 计算域Fig. 1 Computational domain

计算采用FLUENT流体力学软件并采用其中的离散相(discrete phase model, DPM)模型. 采用Euler-Lagrange方法进行计算, 气相控制方程为Euler坐标系中的三维Reynolds平均N-S方程, 液相采用Lagrange轨道模型. 气液两相间的质量、 动量和能量的相互作用, 以源项的形式分别加到气液两相的控制方程中.

液滴运动方程为

其中,up为液滴速度,FD为单位质量液滴受到的阻力,u为连续相速度,g为重力加速度,ρ为连续相密度,ρp为液滴密度,F为其他作用力.

FD的计算公式为

其中,μ为连续相动力黏性系数,dp为液滴直径,CD为阻力系数,Re为相对Reynolds数(液滴Reynolds数).

计算中, 采用基于密度的耦合隐式求解器, 湍流模型采用SSTk-ω模型, 喷雾模型采用雾化锥模型, 液滴二次破碎模型采用K-H/R-T模型. 颗粒阻力系数的准确确定对于喷雾模拟是非常重要的, 本文在计算液滴阻力时采用动态阻力模型, 该模型可以根据颗粒形状的变化动态地确定颗粒的阻力系数. 计算网格采用结构化网格(如图2所示), 壁面第1层网格厚度0.05 mm, 在射流喷孔及壁面附近进行网格加密, 总网格量9.6×105.

图2 计算网格Fig. 2 Computational grids

Lin等[7]采用PDPA技术获得的射流穿透深度拟合关系式, 在射流雾化文献中被广泛地引用并作为与数值模拟结果比较的依据. 本文亦采用Lin等的拟合公式与计算结果进行对比, 其具体形式如下

其中,h表示射流穿透深度,d表示射流喷孔直径,q表示射流/空气动压比,x表示距射流喷孔中心的流向距离.

2 计算结果与讨论

2.1 考虑液滴二次破碎时的情形

本节计算时, 考虑液滴的二次破碎过程, 二次破碎模型采用K-H/R-T模型.

(1)采用雾化锥模型时的计算结果

雾化锥模型认为在射流喷孔出口有一组液滴, 该组液滴以锥形分布喷出. 雾化锥模型是液体射流雾化计算中使用较多的一种雾化模型. 本文采用雾化锥模型, 对图1所示的模型进行了计算. 计算时, 初始雾化锥角选为10°, 初始液滴直径选为100 μm, 液滴二次破碎模型采用K-H/R-T模型. 计算结果如图3所示. 可以看出, 采用雾化锥模型获得的射流穿透深度与采用Lin等拟合公式时的结果符合得很好. 可见, 采用雾化锥模型(与此同时, 要合理设置初始计算参数)对液体射流雾化过程进行模拟是可靠的.

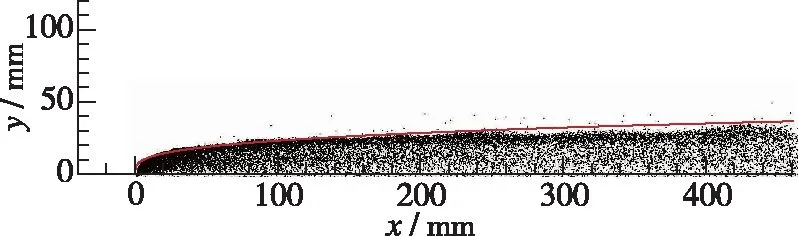
图3 采用雾化锥模型时的液滴分布Fig. 3 Droplet distribution using spray cone model

图4是不同横截面上的液体分布, 其中, 液滴用圆圈表示, 圆圈大小代表了液滴大小. 可以看出, 随着水射流向下游发展, 液滴在Y向和Z向的分布区域均逐渐增大. 观察x=20, 50, 150 mm截面上的液滴分布可以看出, 直径较大的液滴位于液滴群的中心位置, 而直径较小的液滴位于液滴群的边缘位置, 这是因为在液滴群边缘位置处, 液滴与空气气流的相互作用更强, 在更强的气动力作用下, 边缘位置的液滴破碎速度更快. 随着射流进一步向下游发展, 液滴与空气气流不断相互作用, 在x=450 mm 截面上, 液滴的分布已经比较离散, 且液滴直径已经比较均匀.

图5～7为不同截面上的液滴速度分布, 可以看出, 在同一横截面上, 液滴群边缘的液滴与周围空气的相互作用很强, 在空气气流的带动和剪切效应下, 液滴速度很高, 达到600 m/s以上; 而液滴群中心的液滴由于有周围液滴的包裹, 其与空气的相互作用较弱, 因而液滴速度较低. 在x=450 mm 截面上, 由于液滴群不断向Y方向和Z方向扩散, 且液滴与空气不断相互作用, 此时, 整个横截面上的液滴速度均比较高.

图8为x=150 mm截面上液滴速度沿Y方向的计算结果与实验结果的比较. 可以看出, 本文获得的计算结果与实验结果符合得较好. 总的来说, 在靠近壁面的位置, 液滴速度较小, 而在外围靠近空气主流的位置, 液滴速度较大. 沿Y向, 液滴速度呈现先增大后减小, 再逐渐增大的过程.

图9为沿射流喷孔中心对称面上的水蒸气摩尔分数分布. 可以看出, 随着液滴向下游不断运动, 液滴不断蒸发为气相. 水蒸气的分布区域与液滴的分布区域基本一致. 水蒸气的摩尔分数大部分位于2%～4%之间.

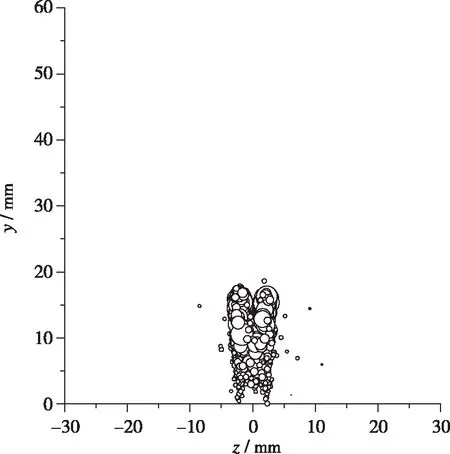
(a) x=20 mm

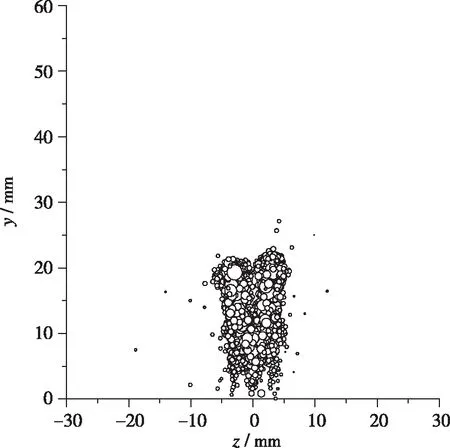
(b) x=50 mm

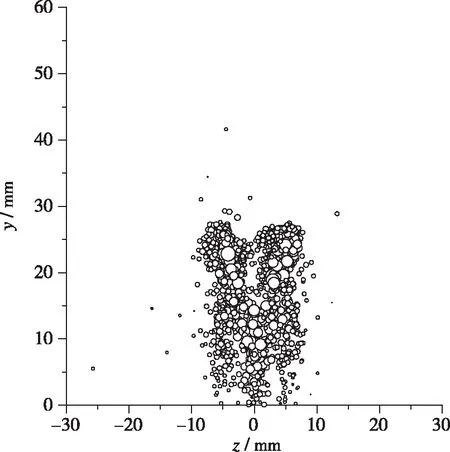
(c) x=150 mm

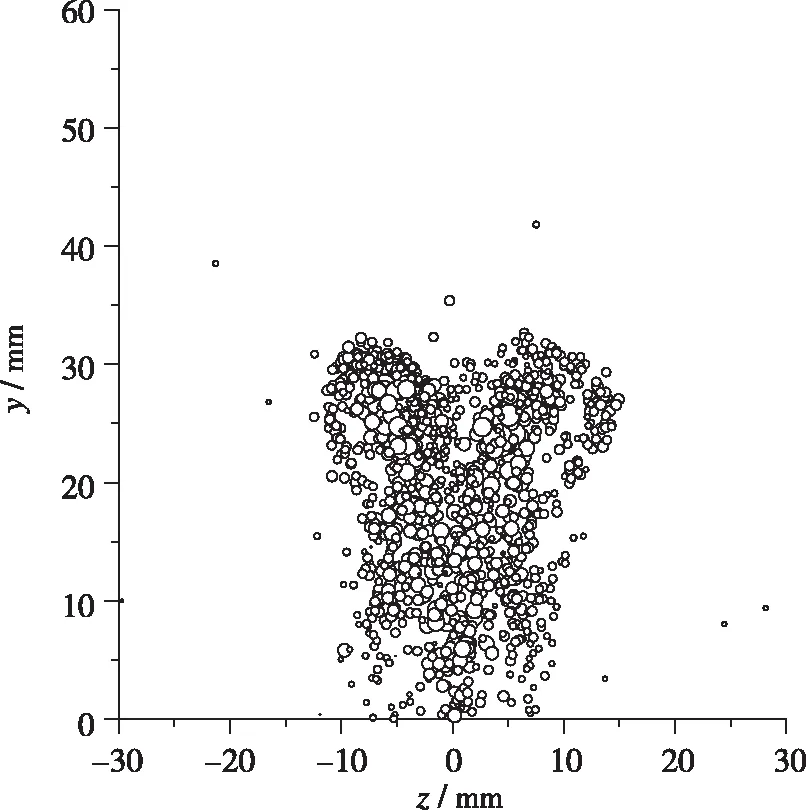
(d) x=250 mm

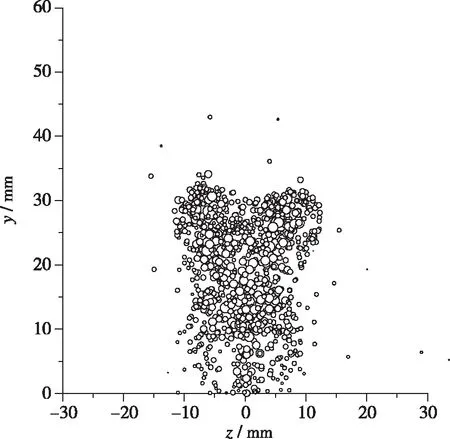
(e) x=350 mm

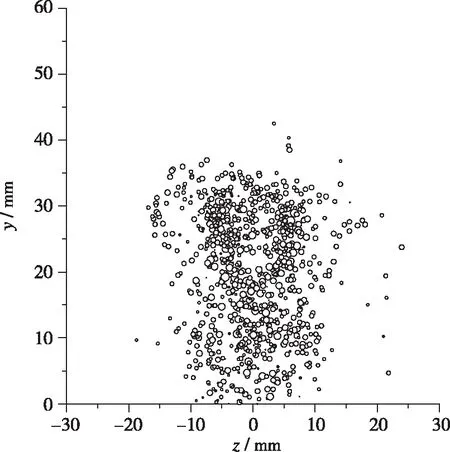
(f) x=450 mm

图5 x=50 mm截面上的液滴速度分布Fig. 5 Droplet velocity on x=50 mm plane

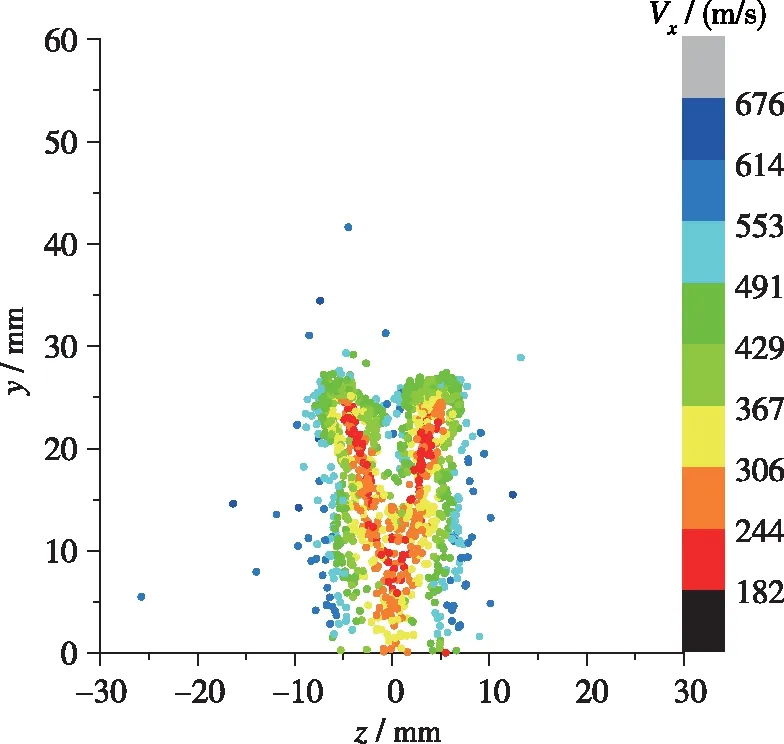
图6 x=150 mm截面上的液滴速度分布Fig. 6 Droplet velocity on x=150 mm plane

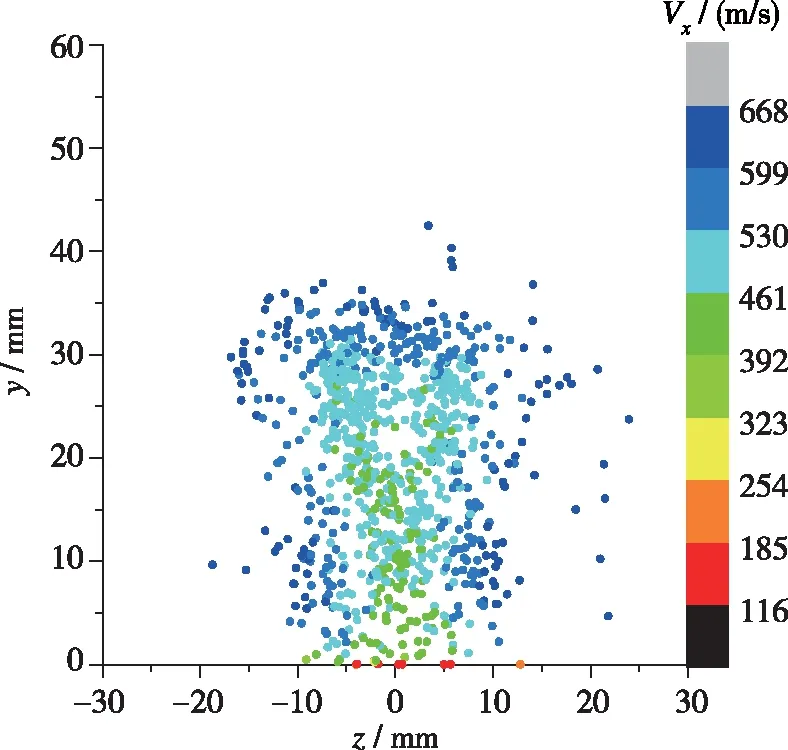
图7 x=450 mm截面上的液滴速度分布Fig. 7 Droplet velocity on x=450 mm plane

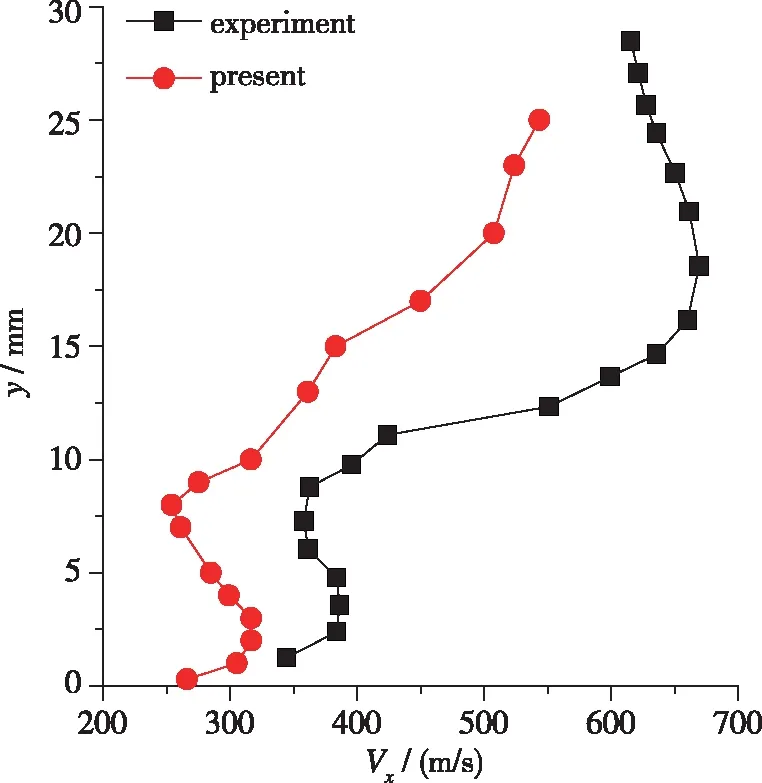
图8 x=150 mm截面上的液滴速度沿Y向分布Fig. 8 Droplet velocity distribution along Y direction on x=150 mm plane

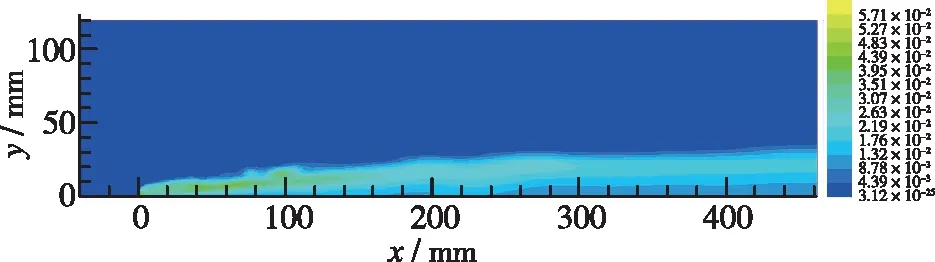
图9 中心对称面上水蒸气摩尔分数分布Fig. 9 Distribution of water vapor mole fraction on the central symmetric plane

(2)初始液滴直径的影响

本节研究了初始液滴直径(即射流喷孔位置的液滴直径)对液滴分布的影响. 根据水射流雾化的实验数据[7], 选取初始液滴直径范围为50～200 μm, 初始雾化锥角均为10°. 计算结果如图10, 3(图3为初始液滴直径100 μm时的计算结果), 11及12所示. 可以看出, 初始液滴直径对射流穿透深度和液滴分布的影响很小, 4种初始液滴直径条件下, 计算获得的射流穿透深度与采用Lin等拟合公式时的结果均符合得很好.

(3)初始雾化锥角的影响

选取初始雾化锥角分别为10°, 40°, 70°这3种工况, 研究了初始雾化锥角对射流穿透深度和液滴分布的影响. 计算时, 选取初始液滴直径均为100 μm. 计算结果如图13～15所示. 可以看出, 随着初始雾化锥角的增加, 相同横截面上的射流穿透深度逐渐减小. 这是因为, 当初始雾化锥角增加时, 液滴在Y方向的速度分量减小, 导致液滴在Y方向的动量减小, 进而导致射流穿透深度减小. 对于3种初始雾化锥角而言, 只有当雾化锥角为10°时, 计算获得的射流穿透深度与采用Lin等拟合公式时的结果符合得很好. 因此, 在开展与本文条件类似的超声速气流中液体横向射流雾化计算中, 建议选择10°左右的初始雾化锥角.

图10 初始液滴直径为50 μm时的液滴分布Fig. 10 Droplet distribution with initial droplet diameter of 50 μm

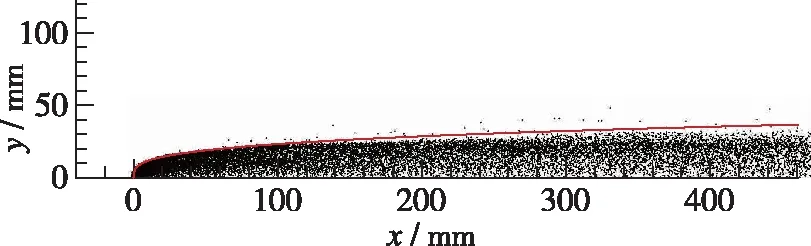
图11 初始液滴直径为150 μm时的液滴分布Fig. 11 Droplet distribution with initial droplet diameter of 150 μm

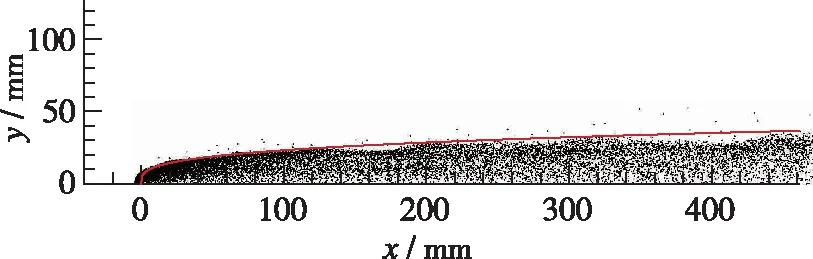
图12 初始液滴直径为200 μm时的液滴分布Fig. 12 Droplet distribution with initial droplet diameter of 200 μm

图13 初始雾化锥角为10°时的液滴分布Fig. 13 Droplet distribution with initial spray cone angle of 10°

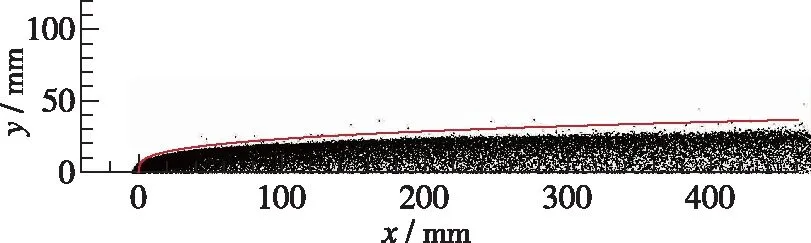
图14 初始雾化锥角为40°时的液滴分布Fig. 14 Droplet distribution with initial spray cone angle of 40°

图15 初始雾化锥角为70°时的液滴分布Fig. 15 Droplet distribution with initial spray cone angle of 70°

2.2 不考虑液滴二次破碎时的情形

在某些液体雾化数值模拟中[15](尤其是计算液体燃料与空气的燃烧流场时), 为了简化计算, 不考虑液滴的二次破碎过程, 直接在射流喷孔给定液滴群的数目, 这种情况下, 液滴在向下游运动的过程中, 不再发生破碎, 仅发生蒸发. 本文对这种情况进行了研究, 计算时选取初始液滴直径分别为20， 5 μm 两种情况, 初始雾化锥角均为10°. 计算结果如图16， 17所示. 可以看出, 液滴直径为 20 μm 时的射流穿透深度与采用Lin等拟合公式时的结果符合得很好, 而液滴直径为 5 μm 时的射流穿透深度与采用Lin等拟合公式时的结果差别很大. 液滴直径为5 μm 时的射流穿透深度明显低于采用Lin等拟合公式时的结果, 这是因为选择5 μm液滴直径时, 液滴动量较小, 进而导致其穿透深度减小. 可见, 当不考虑二次破碎时, 液滴穿透深度及分布与所选的初始液滴直径有很大关系. 如果要采用这种模型(不考虑液滴二次破碎过程)进行雾化计算, 必须根据相关的实验数据和经验选择合适的初始液滴直径, 否则计算结果可能与实际情况有较大的偏差.

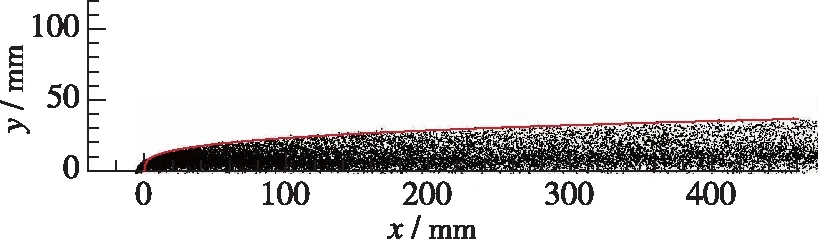
图16 液滴直径为20 μm时的液滴分布Fig. 16 Droplet distribution with droplet diameter of 20 μm

图17 液滴直径为5 μm时的液滴分布Fig. 17 Droplet distribution with droplet diameter of 5 μm

3 结论

本文采用Euler-Lagrange方法对超声速空气中水射流雾化及蒸发过程进行了仿真研究, 研究获得的主要结论如下:

(1)考虑液滴二次破碎过程时, 合理设置初始液滴直径和初始雾化锥角的条件下, 采用雾化锥模型获得的射流穿透深度与采用Lin等拟合公式时的结果符合得很好; 采用本文计算方法获得的液滴速度沿Y向分布规律与实验结果符合得很好; 初始液滴直径对射流穿透深度和液滴分布的影响很小; 随着初始雾化锥角的增加, 相同横截面上的射流穿透深度逐渐减小. 此外, 计算结果表明: 在射流喷孔下游的横截面上, 直径较大的液滴分布于液滴群的中心位置, 而直径较小的液滴分布于液滴群的边缘位置.

(2)不考虑液滴二次破碎过程时, 液滴穿透深度及分布与所选的初始液滴直径有很大关系; 如果要采用这种模型(不考虑液滴二次破碎过程)进行雾化计算, 必须根据相关的实验数据和经验选择合适的初始液滴直径.

致谢感谢中国空气动力研究与发展中心高超声速冲压发动机技术重点实验室基金项目的支持, 感谢国防科技大学李佩波在论文撰写过程中提供的帮助.