基于物理机制模型的民机机体噪声预测
2021-05-19徐康乐陈迎春
徐康乐, 陈迎春, 徐 亮
(1. 上海飞机设计研究院环境集成部, 上海 201210; 2. 中国商用飞机有限责任公司, 上海 201210)
引 言

基于物理机制建模的方法是通过对噪声物理机理的理解, 使用简单有效的模型来描述复杂物理现象, 从而避免对复杂物理现象进行综合求解. 气动声学问题不可避免地涉及高Reynolds数非定常流动. 这些问题是没有解析解的. 同时, 数值解也极具挑战性, 很难应用于飞机噪声的实际问题. 因此, 基于物理机制的建模方法在工程中是非常有效和实用的.
针对飞机级的整机噪声预测, 基于物理机制模型的预测方法被世界主要飞机制造商和航空航天机构所采用, 其中最为典型的方法有NASA Langley中心的飞机噪声预测程序(aircraft noise prediction program, ANOPP)[1-2]和DLR的参数化飞机噪声分析模块(parametric aircraft noise analysis module, PANAM)[3]等. Brooks等通过试验测量所得的表面压力, 基于Howe理论预测了襟翼侧缘噪声[4]; Guo等[5-7], Fink[8]在全尺寸飞机噪声试验数据的基础上发展了预测增升装置气动噪声的物理机制预测方法. 该方法包含有不同飞机在不同飞行状态下机体噪声数据库, 数据库中机体部件噪声的试验数据主要是通过麦克风相阵列技术测得的. 文献[9-13]给出了基于物理机制模型预测机体, 包括起落架、缝翼和襟翼噪声的更多实际应用.
目前, 中国商飞搭建了基于物理机制的飞机级机体噪声预测体系, 形成相应的预测工具UNICRAFT, 见图1. 本文采用UNICRAFT对飞机机体噪声进行了预测. 计算表明基于物理机制的飞机级噪声预测方法可以控制在秒量级, 同时通过将预测结果和试验数据进行对比, 校核验证了该预测工具的可靠性.
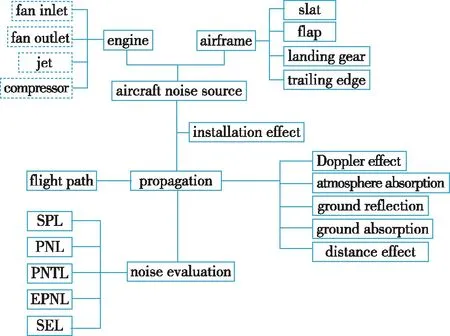
图1 基于物理机制的飞机级外部噪声预测Fig. 1 Physical based aircraft noise prediction

1 基于物理机制的机体噪声建模方法

1.1 基本方程
基于物理机制建模的方法以气动声学的基本理论为出发点, 结合量纲分析、渐近分析、统计分析、相关性分析等对每个噪声分量的声源机理进行建模. 利用能量加法将分量噪声相加得到飞机的总噪声. 对于每个噪声分量, 预测方法包括噪声幅值、远场方向性、谱函数、特征长度、Mach数相关函数、安装效应和其他相关量. 噪声分量的计算首先从窄带频谱函数的模拟开始, 然后导出与窄带频谱有关的Mach数、远场方向性、噪声幅度和安装效果, 最后将窄带频谱积分到倍频程频谱的1/3[14].
假设飞机在具有恒定平均密度ρ0和声速c0的静态声介质中以恒定Mach数飞行. 坐标系选择为相对于麦克风位置固定. 对于低Mach数流动, 根据声类比理论, 表面压力波动引起的远场声压可表达为

(1)
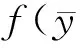
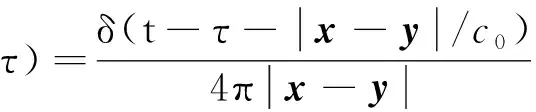
(2)
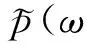
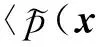
(3)
其中, П表示功率谱密度, *表示复共轭, 〈〉表示系统平均. 由式(1)和(3)可得
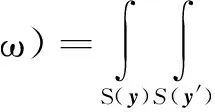
(4)
式中, Пs为表面压力波动的功率谱密度. 从平稳随机过程的一般统计量出发, 表面压力功率谱密度可表示为幅值函数、空间相关函数和时间相干函数的乘积形式
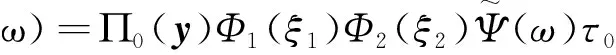
(5)
式中, 空间相关函数在表面上被分成两个分量ξ1和ξ2, 且
y=y′+ξ
(6)
以及
G0(x-y′)=G0(x-y)e-ikξ
(7)
将式(5),(7)代入式(4)可得
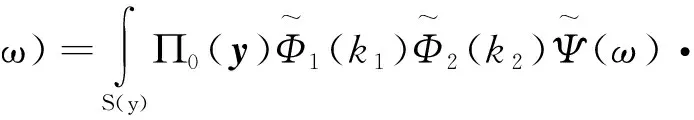
(8)
式(8)即为基于物理机制求解远场声源的一般形式. 通过对式(8)中自功率谱幅值П0及空间相关性Φ1(ξ1)Φ2(ξ2)进行不同形式的模化表征, 以及将Green函数解析表达后, 可以建立起不同部件的预测模型. 通过积分变量模化表征, 式(8)可以转化为如下的解析形式
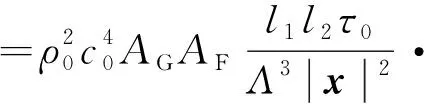
(9)
式中,AG为几何影响因子,AF为流动影响因子,Γ(Ma)为Mach数幂指数率关系,D(θ,φ)为指向性因子,F(St,Ma)为频谱形状, e-α0|x|定义了声衰减关系. 衰减系数可以参照CCAR 36部适航规章相关定义给出. 显然, 不同部件上述影响因子均不同. 本节略去详细推导过程, 直接给出了不同部件的物理机制预测模型, 具体细节见文献[15].

1.2 频谱形状
流动相关函数采用指数函数的形式, 其频域形式
(10)
其中, 频率用来流St的形式表示,μ0为常数. 空间相关函数表示为
(11)
通过空间Fourier变换, 可得波数形式下
(12)
式中,μ1,μ2为常数. Green函数在无量纲形式下对噪声频率谱的贡献
(13)
式中,μ3为常数. 于是, 噪声功率谱密度的谱形状函数
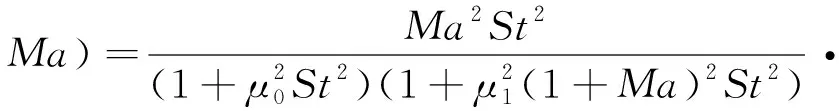
(14)
襟翼侧边缘噪声由两种噪声频谱分量组成. 一种来自于襟翼前缘沿下游的流动分离, 另一种来自襟翼后半弦长处侧缘涡/边缘的相互作用. 两种分量覆盖不同的频率域,由各自主导的St决定. 即
П=ПL+ПH
(15)
式中角标L,H分别代表低频和高频分量. 同时每个分量形式均如式(9)所示. 对于缝翼, 则以不同声源分布位置进行总频谱的合成, 如缝翼凹穴声源ПC, 缝道声源ПG, 导轨声源ПB, 如式(16)所示
П=ПC+ПG+ПB
(16)

1.3 指向性因子
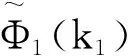
从式(8)可以得出方向性因子的一般形式如下
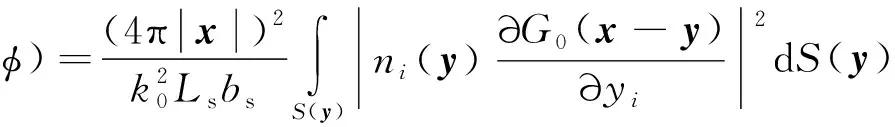
(17)
式中, 积分前系数为保证指向因子为无量纲形式.Ls为缝翼展长,bs为缝翼弦长.θ为飞机下方极角, φ为横侧角. 这两个角度为全局坐标. 积分在缝翼的局部坐标系中可进行, 最终的结果可以通过坐标旋转和平移转换为全局坐标系. 局部坐标系定义如下:
{η1,η2,η3}分别为偶极子极性方向、缝翼弦长方向、缝翼展长方向. 在局部坐标系下远场麦克风坐标为ξ, Green函数为
(18)
通常情况下忽略缝翼厚度影响, 即偶极子只沿着缝翼弦向和展向分布. 由此, 可以将式(17)简化为只沿着η1的法线方向, 即
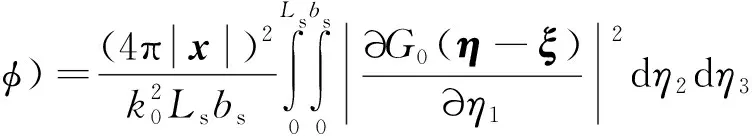
(19)
将式(19)被积函数展开
(20)
将式(20)代入式(19)可以得到指向性解析形式
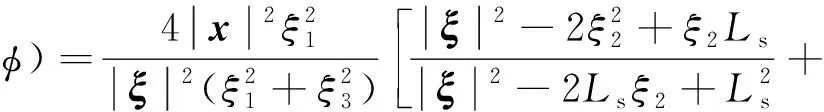
(21)

2 预测与验证

2.1 预测模型输入
物理机制模型预测方法输入参数包括飞机总体参数和部件的几何信息. 宏观几何参数包括定义机身的长度、宽度和高度, 机翼的翼展、最大弦长、最小弦长和后掠角, 前起落架到机身前端的距离和主起落架到前起落架的距离、主起落架到机身的距离, 以及发动机到机身中心线的距离. 部件几何参数包括: 翼根弦长, 翼尖弦长, 翼展, 缝宽, 襟缝翼角度, 襟缝翼类别和其导轨个数.

2.2 机体噪声预测与验证
算例1: 翼吊式布局飞机机体噪声预测验证.
翼吊式布局飞机采用典型的前缘缝翼和单缝Fowler式襟翼形式. 飞机在DNW-LLF声学风洞进行了机体噪声测量. DNW-LLF声学风洞是最早也是最成熟的大型声学试验风洞, 试验段尺寸为 8 m×6 m, 因此试验数据具有较大的可靠性. 模型试验如图2所示, 模型缩尺比例为1∶7.6. 由于风洞试验硬件限制, 远场麦克风极角位置涵盖60°~120°. 图3~7显示了飞机以着陆构型在Mach数为0.2条件下, 基于模型预测结果和风洞试验结果的对比情况. 这里指出, 图3~7所示结果均为修正至全尺寸条件下的飞机机体噪声数据. 因此, 图中横坐标的有效频率截止在2 000 Hz左右. 从图中可以看出飞机全尺寸条件下, 在所有有效极角范围内, 预测频谱和试验频谱幅值偏差均控制在2 dB以内, 且频谱形状与试验结果基本吻合. 因此, 工具UNICRAFT可以有效预测飞机级全尺寸条件下的噪声预测水平.

图2 DNW-LLF声学风洞试验Fig. 2 Airframe noise wind tunnel test in DNW-LLF
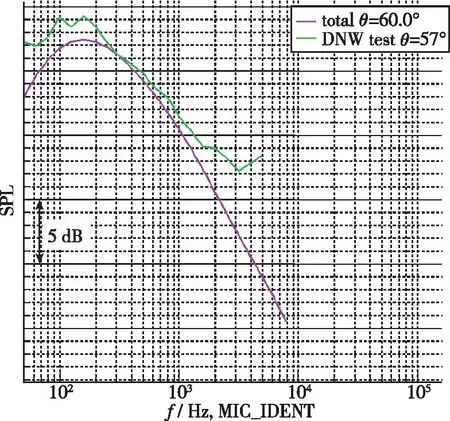
图3 预测和试验结果对比(θ=60°)Fig. 3 Comparison between prediction and test results(θ=60°)
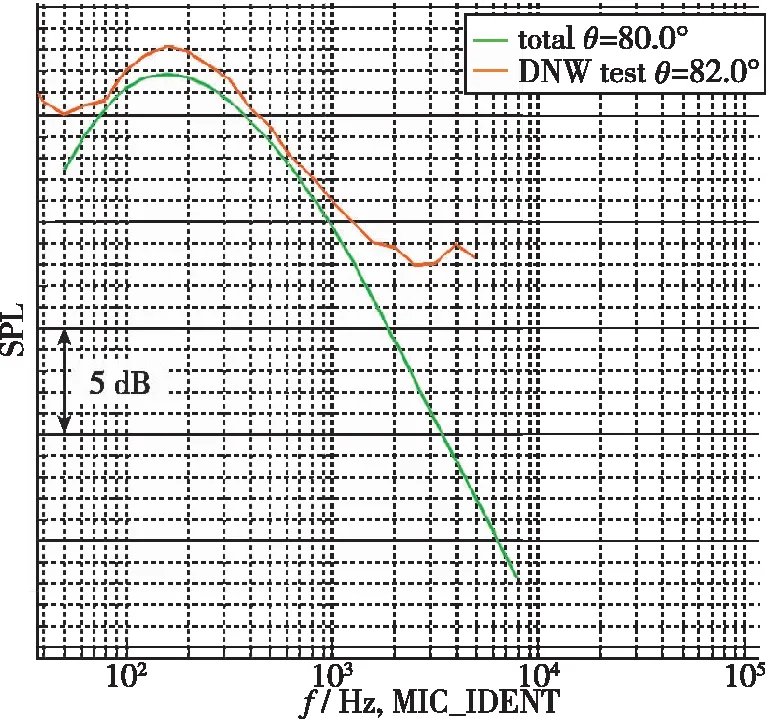
图4 预测和试验结果对比(θ=80°)Fig. 4 Comparison between prediction and testresults(θ=80°)
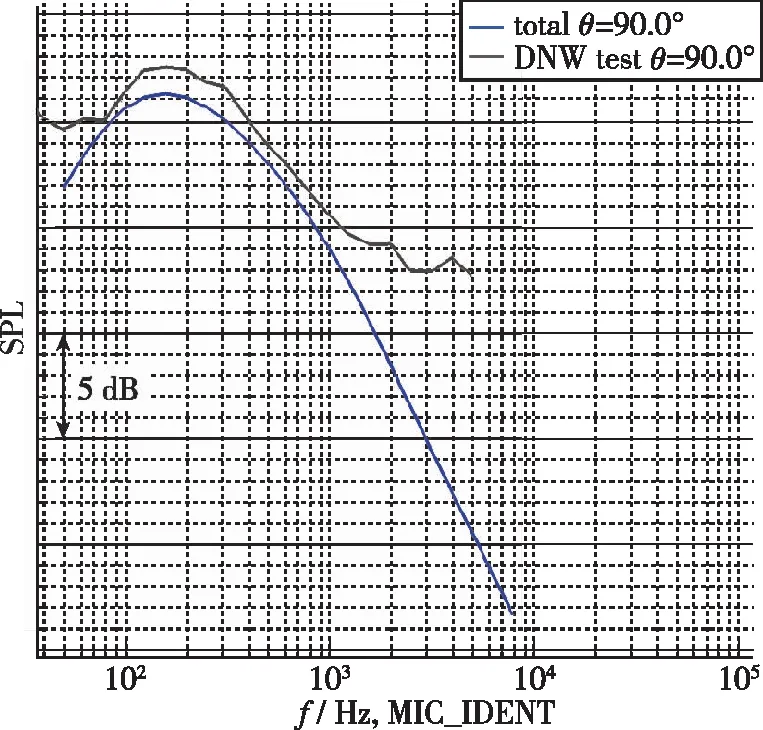
图5 预测和试验结果对比(θ=90°)Fig. 5 Comparison between prediction and test results(θ=90°)
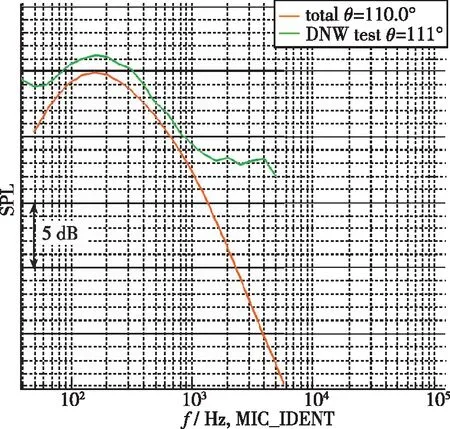
图6 预测和试验结果对比(θ=110°)Fig. 6 Comparison between prediction and test results(θ=110°)
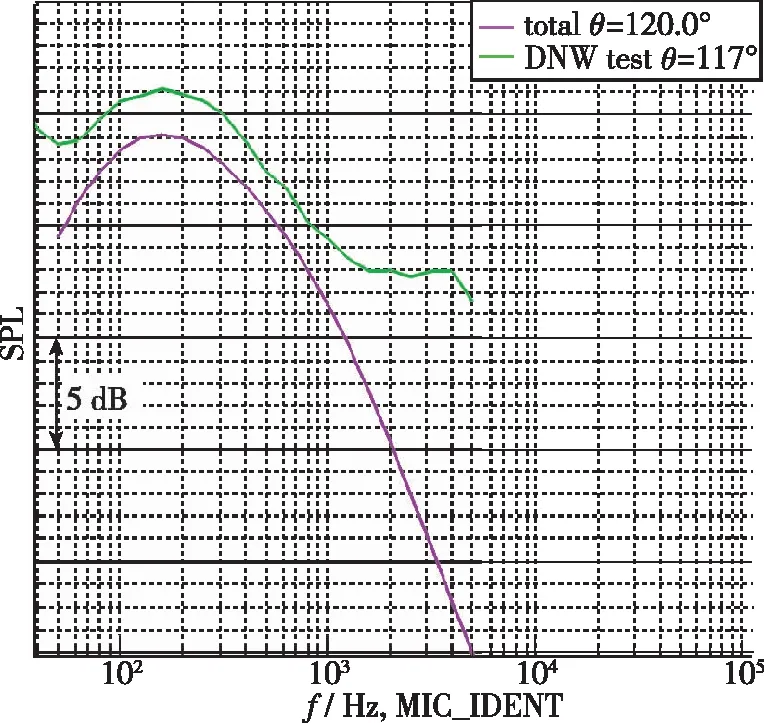
图7 预测和试验结果对比(θ=120°)Fig. 7 Comparison between prediction and test results(θ=120°)
算例2: 尾吊式布局飞机机体噪声预测验证
尾吊式布局飞机采用前缘缝翼和双缝子翼加后退式襟翼形式. 该模型采用半模开口式声学风洞试验, 试验段尺寸5.5 m×4 m, 试验模型比例1∶7, 具体如图8所示. 图9、 图10分别给出了起飞构型条件下不同Mach数预测结果和风洞试验结果的对比. 该算例试验数据只做了半模至全模修正、壁面反射和风洞剪切层修正等, 未开展全尺寸修正.

图8 飞机机体半模声学风洞试验Fig. 8 Half model noise test in wind tunnel
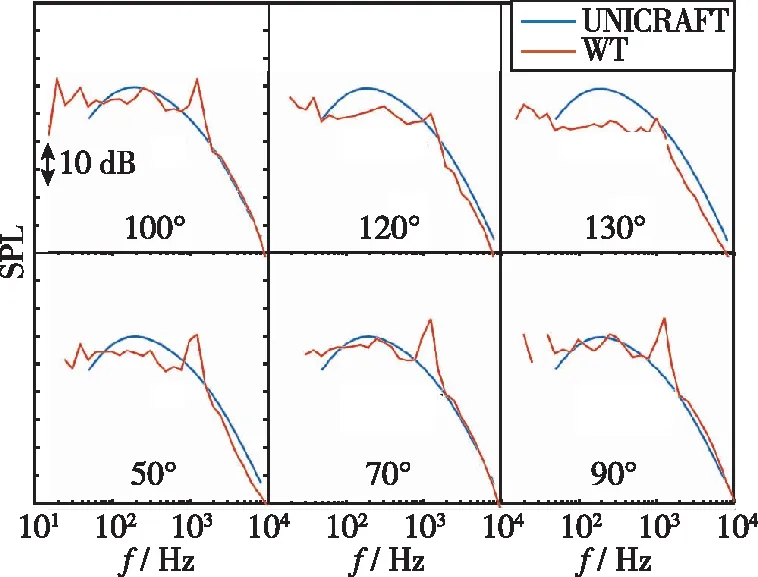
图9 各极角位置预测与风洞试验结果对比(起飞构型, Ma=0.15)Fig. 9 Comparison between prediction and test results(takeoff configuration, Ma=0.15)
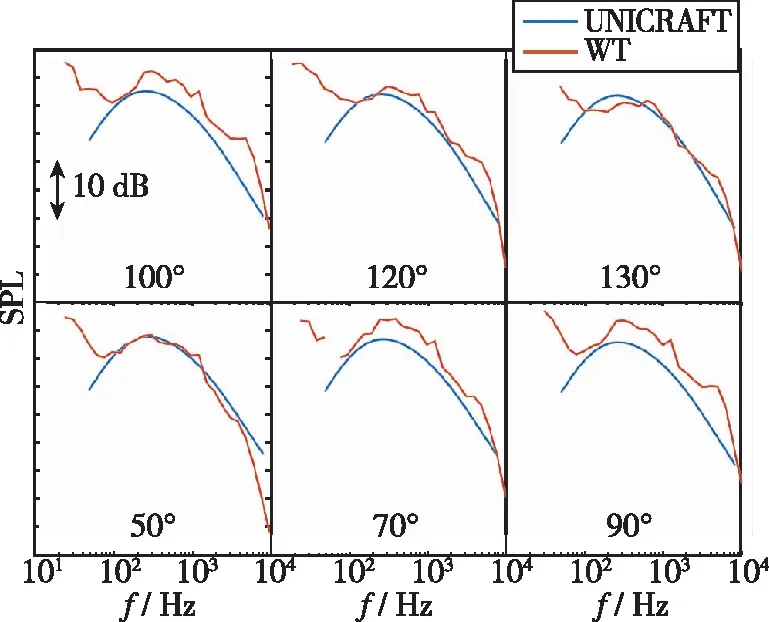
图10 各极角位置预测与风洞试验结果对比(起飞构型, Ma=0.22)Fig. 10 Comparison between prediction and test results(takeoff configuration, Ma=0.22)
从图9、 图10可以看出预测结果在试验有效极角范围内幅值和频谱均与试验结果吻合良好, 具有很好的工程预测精度.

3 结论

本文基于物理机制模型预测了不同飞机布局及增升装置形式下的机体噪声水平, 并与声学风洞试验结果进行了对比验证. 结论如下:
(1)基于物理机制的飞机级机体噪声预测方法能够高效地预测机体噪声水平, 计算时间可以控制在秒量级;
(2)本文发展的计算工具UNICRAFT其精度满足工程预测要求. 预测和试验结果的误差在试验有效极角和频段范围内不超过2 dB;
(3)基于物理机制的UNICRAFT机体噪声预测工具能够有效支持飞机总体方案评估、优化迭代以及飞机级需求分解等工作.
