受限空间内旋流回流区特性

2021-05-19李玉栋涂晓波王林森

气体物理 2021年3期

关键词：旋流流线燃烧室

李玉栋, 张俊, 陈爽, 涂晓波, 王林森

(中国空气动力研究与发展中心, 四川绵阳 621000)

引言

旋流广泛存在于燃烧器、工业锅炉、燃气轮机、航空发动机等设备中[1]. 足够高的旋流强度, 会使流场中产生逆压梯度, 形成中心回流区, 能够增加火焰稳定性, 提高燃料掺混程度和燃烧效率.

旋流从喷嘴进入燃烧室经历突然扩张的过程, 通常用燃烧室直径与喷嘴直径的比值受限率表示旋流在燃烧室内的受限程度, 受限率越小, 表示流体受限的程度越强. 有研究表明[2]受限率是旋流器、燃烧室结构设计参数中对旋流影响最显著的因素.

对于中心回流区, Sheen等[3]最早根据Reynolds数和旋流数划分了7种形态, 除了最后的合并形态, 其余6种在受限和非受限空间中差别很小. Archer等[4]采用粒子图像测速法(particle image velocimetry， PIV)研究了受限率为2的情况, 表明受限空间增加了中心回流区的湍动能, 减小了回流区宽度和回流速度. Fu等[5-6]采用激光Doppler测速法(laser dopler velocimetry， LDV)研究了不同受限空间内的旋流流动, 发现旋流杯尺寸为4.3 in × 4.3 in(1 in=25.4 mm)时, 产生了一个过渡的旋流状态, 与其他情况有显著的差异. 此外, Khalil等[7]、 Sharma等[8]研究了受限率分别为1.7和5.4的旋流流场. 以上都是对二维流场的研究. Ceglia等[9]采用层析PIV测量了受限率等于3.2时的三维流场, 并通过本征正交分解(proper orthogonal decomposition， POD)和低阶重构方法(low order reconstruction, LOR)重构了旋流场涡结构. 用涡核进动的三维结构, 直观地展示了旋流扩张角及回流区增大的情况.

采用光学测量方法研究受限空间旋流流场特性时, 由于结构限制、壁面激光反射等因素, 往往难以获得近壁面及空间视线死角的流动情况. 因此, 数值模拟也广泛应用于旋流流场的研究, 同时也可与实验数据相互验证. Guo等[10-12]采用标准k-ε湍流模型和超大涡模型(very large eddy simulation, VLES)模型, 研究了不同旋流数的旋流形态和涡核进动频率, 指出k-ε湍流模型可以很好地预测旋流的基本特征和涡核进动. Paik等[13]采用分离涡算法(detached eddy simulation， DES)模型研究了不同旋流数速度剪切层和速度分布沿流向的变化、旋流流场湍流拟序结构和回流区形态. Nogenmyr等[14]采用大涡模拟法(large eddy simulation， LES)模拟旋流流场并与PIV实验对照, 分析了边界条件设置的影响. Xia等[15]对比了VLESk-ε模型、 VLESk-ω模型与标准k-ε模型、k-ω模型, 指出VLES模型能够更好地预测旋流回流区结构和速度分布.

对于受限空间旋流过渡状态, 目前研究较少, Fu等[6]也只是研究了二维平均流场, 而旋流是一种三维非定常复杂流动, 二维流场中往往难以对回流区的特征现象进行全面描述. 本文在Fu的研究基础上, 借鉴了数值模拟的相关结论[10-12], 采用ANSYS Fluent软件的realizablek-ε湍流模型模拟了旋流数等于0.884时不同受限空间内的非定常旋流流场, 研究了旋流在不同受限条件下, 回流区及涡结构的发展过程, 并分析了过渡状态的特殊涡核进动形式及流场参数分布.

1 计算模型及网格划分

1.1 计算模型

如图1所示, 流体经过旋流器产生切向速度, 进入燃烧室, 燃烧室高度200 mm, 不同燃烧室宽度分别为30， 40， 52， 62， 92 mm. 燃烧室入口轴向速度(箭头方向)大约为8 m/s, 采用非结构网格, 燃烧室网格如图2所示.

图1 计算域示意图Fig. 1 Sketch map of computational domain

图2 燃烧室网格Fig. 2 Grids of the chamber

旋流数采用Beér等[16]的公式计算

(1)

φ=nσ/(2πRcosα)

(2)

式中，S为旋流数,φ为阻塞度系数,α为旋流片角度(弧度),n为旋流叶片数,σ为旋流叶片厚度,R为套筒内径.

数值计算基于ANSYS Fluent软件, 湍流模型采用realizablek-ε模型, 压力速度耦合项采用SIMPLE算法, 动量方程采用2阶格式离散, 湍动能和湍流耗散率方程采用QUICK格式, 近壁面采用标准壁面函数处理[17-19], 时间步长0.01 s[11].

1.2 网格无关性验证

在30 mm的燃烧室进行不同密度的网格划分, 网格数分别是1.5×106， 2.0×106， 2.5×106. 在相同的参数设置下进行计算, 通过对比不同网格数下的中心回流区来验证网格无关性. 如图3所示, 1.5×106网格的中心回流区明显偏大, 2.0×106和2.5×106网格的中心回流区相差很小, 说明计算网格达到2.0×106时, 计算结果与网格数无关. 自由空间、 40 mm 燃烧室、 52 mm燃烧室、 62 mm燃烧室、 92 mm燃烧室的网格数分别为9.0×106， 3.2×106， 5.0×106， 7.0×106， 1.5×107.

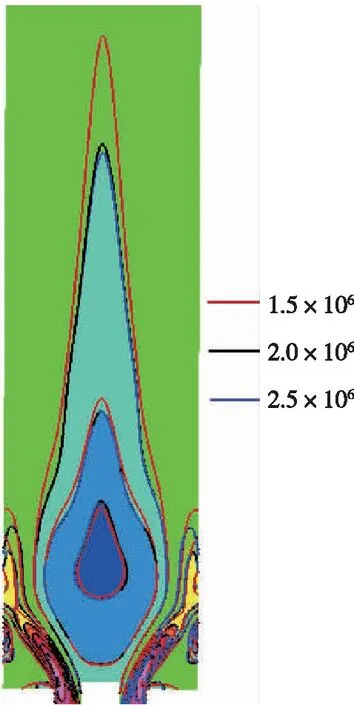
图3 网格无关性验证Fig. 3 Grid independence verification

2 计算结果及分析

2.1 不同受限空间的回流区形态

表1给出了不同燃烧室的参数, 包括壁面宽度L，受限率C，旋流数S, 其中S由公式(1)(2)得到.

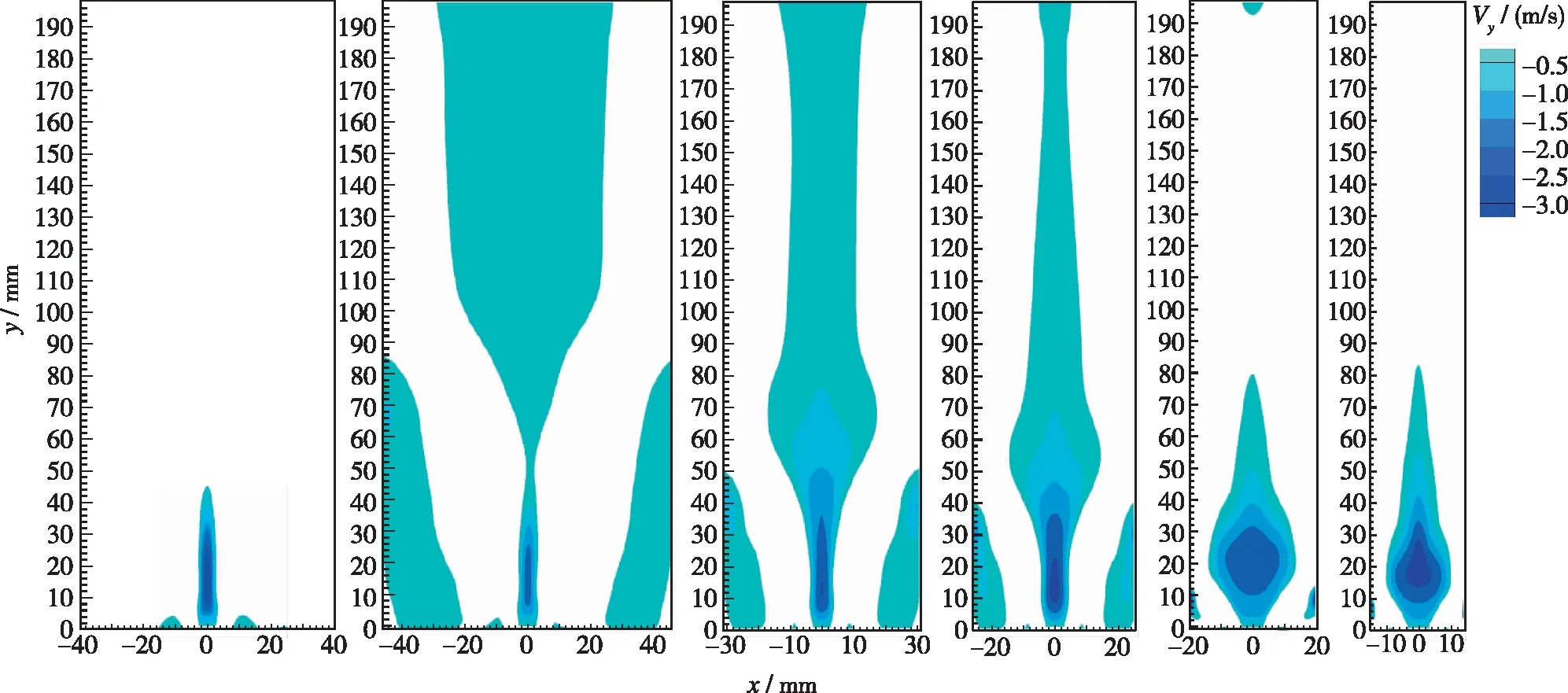
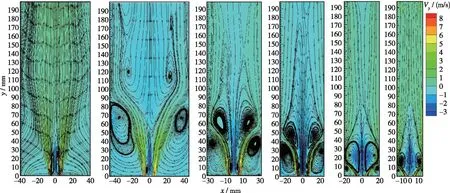
计算结果如图4， 5所示, 为中心处截面. 图4， 5中(a)～(f)分别对应表1中工况1～6. 其中, 自由空间(工况1)的流场只截取了-40～40 mm的部分.

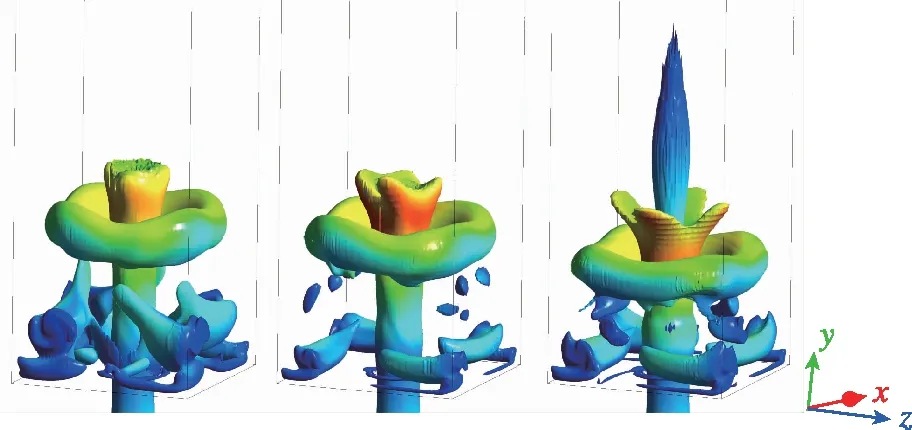
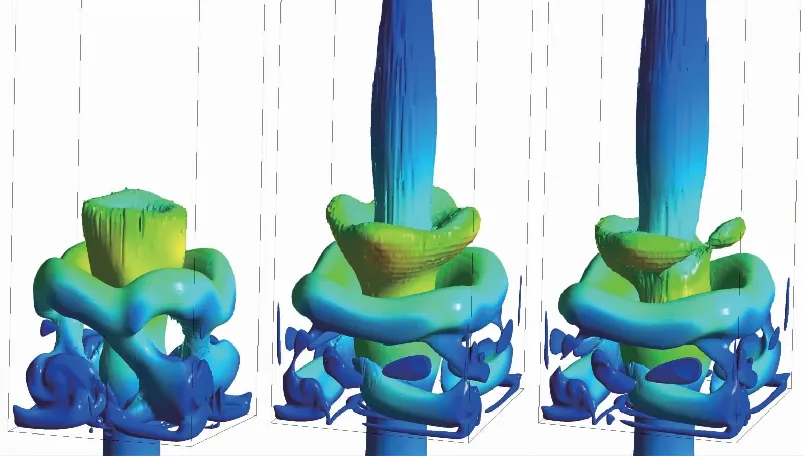
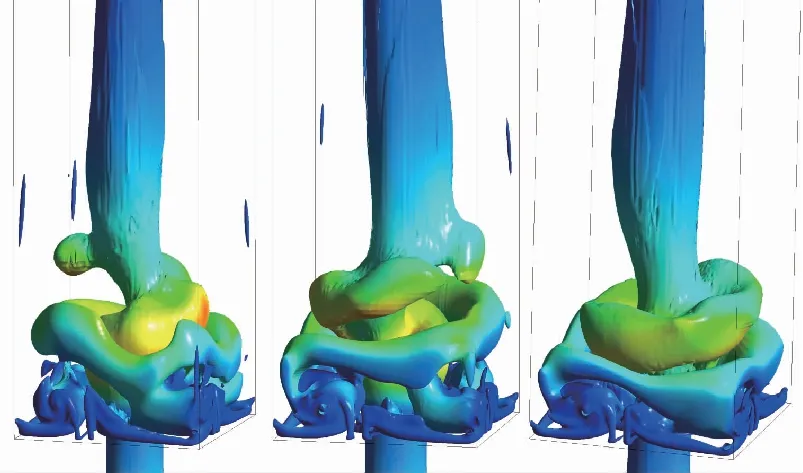
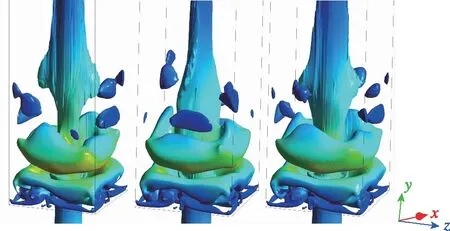
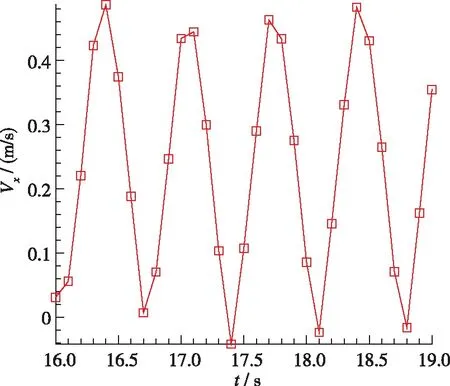
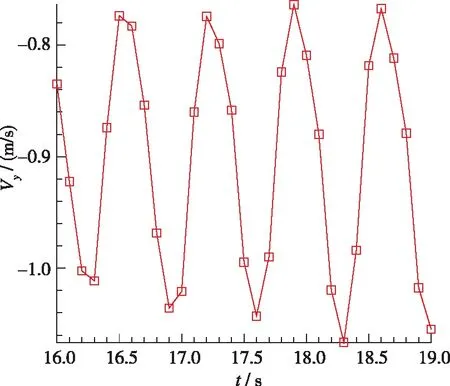
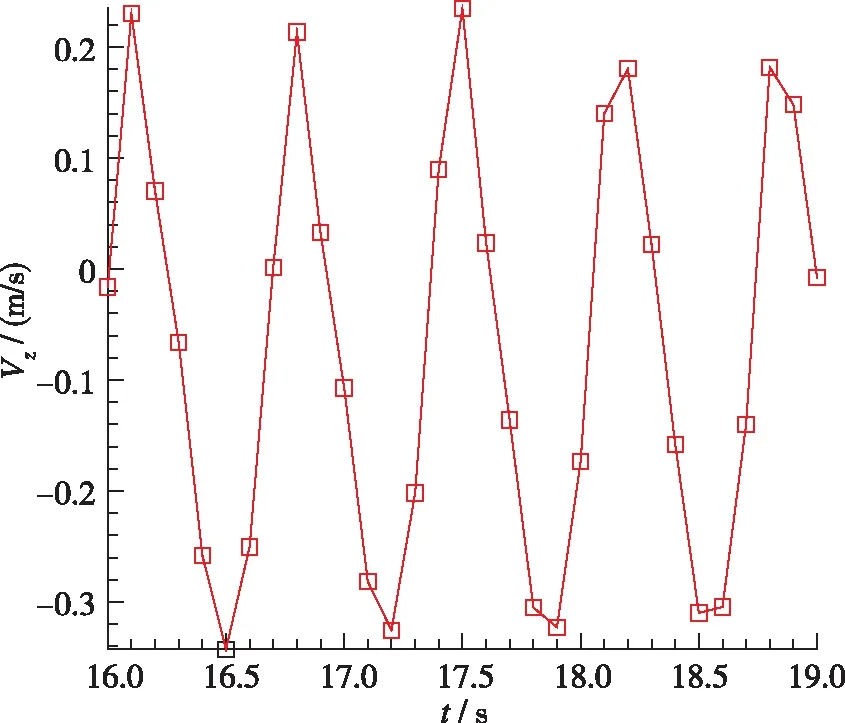
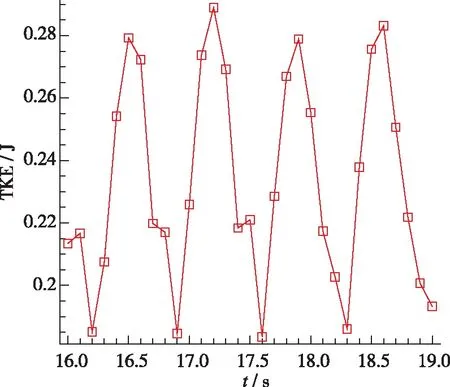
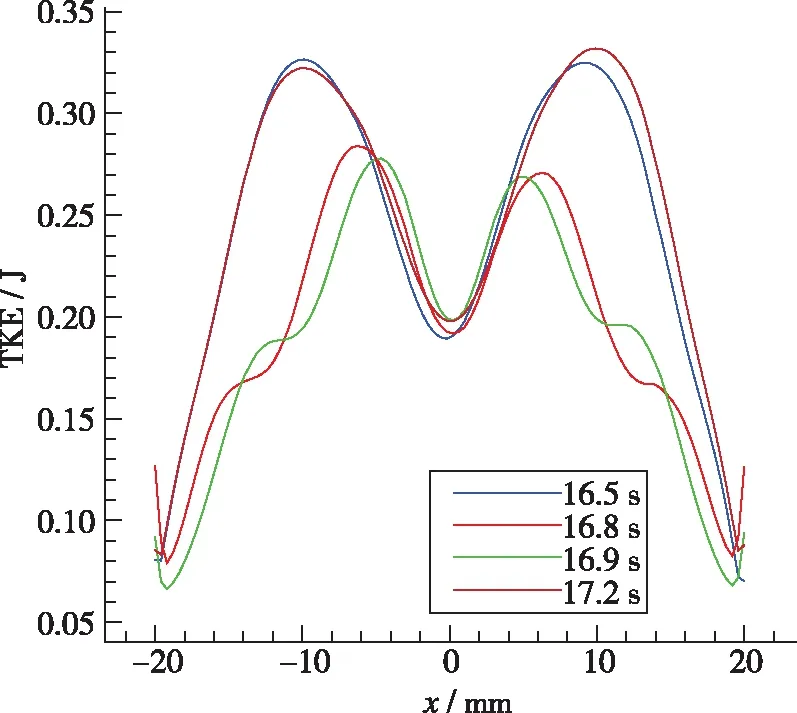
自由空间和受限空间中, 都会出现中心回流区. 受限空间中, 流场中还会出现角回流区. 如图4(a), 5(a), 在自由空间内, 由于旋流数较小, 中心回流区只存在于钝体上方狭长的区域内, 高度约45 mm. 对于受限空间, 随着壁面宽度减小, 壁面对旋流的限制作用逐渐增强, 回流区主要呈现3种不同的形态. 图4(b), 5(b)中, 壁面宽度为92 mm, 中心回流区的形态与自由空间内的中心回流区没有明显差别, 可以看到在入口处有一对涡. 在流场下游, 流线扩张, 流体与壁面撞击反弹, 在出口附近又出现较弱的回流区和另一对涡, 这两个回流区是两个独立的区域. 图4(c)(d)， 5(c)(d)中, 壁面宽度分别为62 mm和52 mm, 流线扩张角度增大, 与壁面的作用加强, 下游回流区向上游移动, 与中心回流区合并, 使中心回流区宽度明显增大,但上下游的两对涡并没有合并. 图4(e)(f)， 5(e)(f)中, 壁面宽度分别为40 mm和30 mm, 流线继续扩张, 角度明显增大, 下游回流区与中心回流区合并形成一个大的中心回流区, 同时两对涡合并, 角回流区减小. 综上所述，可根据受限率C将回流区形态大致划分如下:C>6时, 中心回流区与下游回流区是两个独立的区域, 有两对涡结构, 中心回流区的形态与自由空间内的回流区差别不大; 3

表1 燃烧室参数

(a) Case 1 (b) Case 2 (c) Case 3 (d) Case 4 (e) Case 5 (f) Case 6图4 不同受限空间的回流区Fig. 4 Recirculation zone of different cases

(a) Case 1 (b) Case 2 (c) Case 3 (d) Case 4 (e) Case 5 (f) Case 6图5 不同受限空间的速度流线Fig. 5 Velocity pathlines of different cases

2.2 过渡状态的回流区发展过程

对不同受限空间中旋流流场的发展过程进行分析, 工况3， 4， 6的回流区, 不管是纺锤形还是气泡形, 形成之后都会稳定地存在于流场中.

工况5的回流区发展过程与其他几种情况不同. 如图6(a), 工况5的回流区和速度流线与工况3, 4相似, 上下游的两个回流区合并到一起, 有两对涡, 流线的扩张角度较小. 随后出现扰动, 流线变得混乱, 对称的涡结构被破坏, 回流区变得扭曲不规则, 这种扰动传播到下游, 使下游的流线扭曲, 出现了不对称的回流. 然后, 流线扩张角增大, 中心回流区增大, 形成了对称的两对涡, 之后两对涡合并为一对, 发展成图4(e)和图5(e)所示的气泡状回流区. 值得一提的是, 工况6在流场发展初期也出现了类似工况5的狭长回流区和两对涡结构, 但是由于壁面的限制作用, 两对涡很快合并成了一对涡, 并一直保持稳定. 综上所述, 工况5是文献[6]中的过渡状态, 一方面, 工况5的壁面宽度比工况6大, 限制相对较弱, 所以才能在中心回流区下游产生另一对涡; 另一方面, 工况5 的壁面宽度又比工况4小, 限制作用较强, 上下游的两对涡并不稳定, 还会进一步演化变成图4(e)和5(e)或6(g)(h)所示的形态.

(a) t=3 s (b) t=3 s (c) t=6 s (d) t=6 s (e) t=8 s (f) t=8 s (g) t=16 s (h) t=16 s 图6 工况5不同时刻的回流区和速度流线Fig. 6 Recirculation zones and velocity pathlines of case 5

2.3 过渡状态的涡核进动形式

采用q准则来识别流场中的三维涡结构. 如图7～9所示, 不同受限条件下q=0.055的等值面计算结果, 以涡黏性系数着色, 分别对应工况4， 5， 6. 从工况4的中心回流区外围可以看到非常弱的涡核进动痕迹, 呈多螺旋形态; 在下游, 涡黏性系数增大, 动量交换强烈, 涡主要向外围扩散, 此处的多螺旋涡核进动消失. 随着涡的扩散, 涡黏性系数减小, 流场达到平衡, 最终形成两个回流区保持稳定. 工况6的多螺旋涡核进动非常明显, 和工况4一样, 涡黏性系数较大的涡向外围扩散, 但是由于壁面的限制较强, 无法进行充分的动量交换, 所以在下游仍然有明显的多螺旋涡核进动, 最终在两种动量交换形式作用下, 形成了稳定的单个回流区. 工况5中除了带状的涡核进动方式外, 还出现了两种新的涡核进动方式. 工况5形成了类似于工况4的涡结构之后并不稳定, 出现了涡破碎和脱落, 产生一种单螺旋涡核进动方式, 如图8(d)(e). 单螺旋中涡黏性系数较大的涡核通过涡扩散进行动量交换, 最终形成中心回流区, 另一部分涡核继续向下游进动, 形成双螺旋的涡核进动方式. 双螺旋的涡核进动使流场中产生了一个旋转的下游回流区, 当下游回流区旋转到截面处时, 截面上正好可以看到两对涡, 如图6(h)所示; 当下游回流区没有旋转到截面位置时, 只能看到一对涡, 如图5(e)所示. 涡核进动的方向也发生了变化, 多螺旋涡核进动是顺时针旋转(逆流动方向观察), 而单螺旋和双螺旋涡核进动是逆时针旋转.

(a) t=0.2 s (b) t=0.5 s (c) t=3.5 s图7 工况4的q等值面(q=0.055)Fig. 7 Iso-surface of q=0.055 of case 4

(a) t=1 s (b) t=3 s (c) t=4 s

(d) t=6 s (e) t=8 s (f) t=10 s

(g) t=16 s (h) t=24 s (i) t=36 s 图8 工况5的q等值面(q=0.055)Fig. 8 Iso-surface of q=0.055 of case 5

(a) t=1 s (b) t=2 s (c) t=3 s (d) t=4 s图9 工况6的q等值面(q=0.055)Fig. 9 Iso-surface of q=0.055 of case 6

图10为监测点处的3个速度分量和湍动能随时间的变化曲线, 监测点位于图6(h)下游回流区涡结构的中心处. 可以看到4个流场参数均呈周期性变化, 周期为0.6～0.7 s. 图11给出了一个周期内湍动能沿径向的分布变化情况, 其中16.5 s和17.2 s时刻, 双螺旋涡结构的位置对应图6(h)和8(g), 16.8 s和16.9 s时刻, 对应图4(e)和8(h). 当下游回流区的双螺旋涡结构旋转到图6(h)的截面位置时, 由于涡的存在, 流线扩张, 与壁面的作用强烈, 速度脉动增大, 所以其湍动能更大且峰值更靠近壁面; 当双螺旋结构在其他位置时, 由于没有涡的扰动, 所以湍动能较小, 且峰值靠近中心.