基于LADRC的APF在电动钻机电网中的研究*

闫宏亮 李雷明 李家鹏

(西安石油大学电子工程学院；陕西省油气井测控技术重点实验室)

0 引 言

电动钻机动力系统中的钻机绞车、钻井泵及转盘的功耗约占系统装机容量的70%，产生大量的谐波，其中以5、7次谐波最为显著[1-2]。传统的LC滤波器将滤波器的谐振次数设定为与所需滤除的谐波次数一样来达到滤除该次谐波的目的，虽然其结构简单、成本低，但只能滤除指定次谐波且容易发生串、并联谐振，不足以应对电动钻机电网中实时变化的母线谐波电流。有源电力滤波器[3](Active Power Filter，APF)能对大小和频率变化的谐波进行补偿，动态性能良好，其应用可克服LC滤波器等传统谐波抑制方法的缺点[4]，且APF适用于小容量非线性负载的场合，故在电动钻机动力系统中APF可为滤除谐波提供有效解决方案。

补偿电流的跟踪控制和直流侧电压的稳定控制是保证APF良好运行的关键技术。传统的电流跟踪控制方法采用PID控制，但PID控制的稳定性与动态品质存在矛盾，快速性与超调存在矛盾。文献[5]提出了基于重复控制的电流双闭环控制方法，并设计了双闭环电流控制器，相比于单独使用PI控制器较好地提升了APF动态性能和稳态性能。文献[6]提出一种超螺旋二阶滑模控制的电流跟踪控制方法，将高频抖振输出信号转移到高阶，使得APF有更好的性能。文献[7]提出一种基于模型预测控制的单目标预测控制法，通过建立电流跟踪误差的指标函数，采用输出电平作为控制变量，减少了计算量。自抗扰控制[8](Active Disturbance Rejection Controller，ADRC)由传统PID控制演变而来，继承了传统PID误差反馈的核心理念。自抗扰控制器由跟踪微分器(TD)、扩张状态观测器(ESO)和非线性误差反馈控制律(NLSEF)等3部分组成。ADRC在电机控制、航空航天飞行器和风电机组等方面都有广泛的应用，大量研究表明，其控制性能和抗扰特性均优于传统的PID控制。文献[9]将自抗扰控制应用在风电机组中，相比于传统的PD控制器具有更好的鲁棒性，但计算略微复杂。文献[10]将自抗扰控制用于逆变器控制中，设计了一种基于微分前馈的自抗扰控制器，将参考信号的微分通过前馈补偿的方式来减小系统的稳态误差。文献[11]将ADRC应用在高速飞行器中，简化了控制系统设计，增强了系统的跟踪性能和抗扰性能。文献[12-13]将自抗扰控制用于永磁同步电机控制中，有效提升了电机针对时变输入的跟踪精度及抗扰性能。文献[14]将线性自抗扰控制器应用于APF的电压外环控制中，有效提升了微网中APF的稳定性能、直流侧电压的暂态响应速度及谐波补偿效果。

本文针对电动钻机电网中较为严重的谐波问题，将线性自抗扰控制器应用于有源电力滤波器的电流跟踪控制中，保证APF的补偿电流能较为实时地跟踪指令信号变化。通过对电动钻机电网APF进行建模分析得到简化的系统数学模型，进而得到其状态空间模型，以此设计线性扩张状态观测器(LESO)和线性状态误差反馈控制律(LSEF)，从而得到其电流跟踪控制器模型。对比传统的PID控制，该控制策略提高了APF的滤波性能和抗扰性能，从而保证电动钻机电网电能质量和电动钻机动力系统的安全稳定运行。

1 电动钻机电网APF模型建立

1.1 电动钻机电网APF结构

针对电动钻机电网中钻机绞车(DW)、钻井泵(MP)、转盘(RT)等谐波源对电动钻机电网造成的电能质量问题，建立如图1所示的电动钻机电网APF系统结构。

图1 电动钻机电网APF系统结构Fig.1 APF structure of electric drilling rig power grid

图1中ua、ub、uc为三相电压源，另用Za、Zb、Zc表示三相电网阻抗，ia、ib、ic和in为APF主电路发出的补偿电流，IS为电网电流，IL为负载电流，C为直流侧电容。三相四线制APF主电路采用四桥臂式，产生各相的补偿电流，N相可单独对中性线上的补偿电流进行控制。

1.2 APF数学模型

将图1简化为如图2所示的开关等效电路。图2中uA、uB、uC、uN为各桥臂电流输出点电位，ia、ib、ic分别为三相电流，R为交流侧等效电阻，L为交流侧等效电感，ud为直流侧电容两端电压。Sj为开关函数，表示开关器件的开关状态，其中j=A、B、C、N。Sj=1表示开关处于导通状态，Sj=0表示开关处于关断状态。

图2 APF等效电路图Fig.2 APF equivalent circuit diagram

为了简化模型，对APF系统进行理想化处理。系统中所有开关器件均为不考虑开关损耗及开关时间的理想器件，三相电源电压对称且只含基波正序分量，即满足ua+ub+uc=0。

针对图2所示拓扑结构，由基尔霍夫电压定律和基尔霍夫电流定律可得APF开关函数的数学模型，如式(1)和式(2)所示。

(1)

(2)

在开关频率很高的前提下，忽略开关函数的高频谐波成分，利用状态空间平均法用占空比dj代替开关函数Sj，简化系统数学模型，得到APF的低频模型：

X′=AX+BU

(3)

式中：

(4)

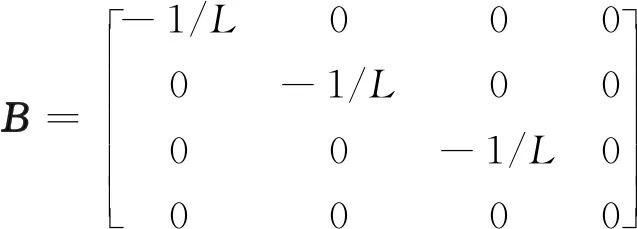
(5)

(6)

(7)

2 线性自抗扰控制器的设计

2.1 线性自抗扰控制原理

自抗扰控制是由中国科学院韩京清研究员提出的一种解决非线性(包括线性)不确定性系统的控制策略。自抗扰控制的核心思想就是将系统的内扰和外扰统一视为系统的总扰动，然后通过ESO对总扰动进行观测和补偿，以实现对系统的稳定控制。自抗扰控制由跟踪微分器(TD)、扩张状态观测器(ESO)和非线性状态误差反馈(NLSEF)等3部分组成，这3部分均采用非线性函数，参数众多且调整参数的过程复杂，控制器设计较为繁琐。但自抗扰控制器在正常运行时基本工作在线性区，美国克利夫兰大学高志强教授将ADRC线性化，提出了线性自抗扰控制技术(LADRC)[15-16]。LADRC在保证自抗扰控制器性能优良的同时能减少控制参数，且便于计算。

图3为n阶LADRC的结构图，以此为例对LADRC进行推导。线性扩张状态观测器LESO为：

(8)

通过对β1、β2、……、βn+1的选取，估计出系统总扰动zn+1，同时得到y以及其各阶微分的估计值z1、z2、……、zn。

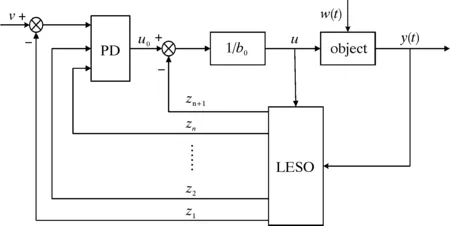
图3 n阶LADRC结构图Fig.3 Structure diagram of n-stage LADRC

线性状态误差反馈控制律变为PD控制器形式，即：

u0=kp(v-z1)-kd1z2-……-kd(n-1)zn

(9)

本文选择适当的kp、kd1、kd2、……、kd(n-1)来构造控制分量u0，进而获得LADRC的控制量u，计算式如下：

(10)

式(8)、式(9)和式(10)构成了n阶LADRC。其中PWM控制方式在采用三角波调制情况下，占空比满足：

(11)

式中：vrj为j相谐波补偿电流瞬时值，Vtri为三角波幅值

将式(11)代入式(3)，可得：

(12)

化简为：

(13)

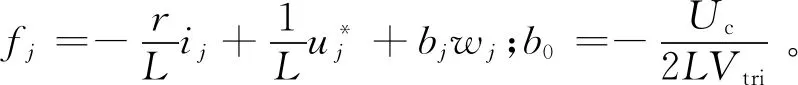
2.2 线性扩张状态观测器

将式(10)写为状态空间形式，即：

(14)

状态空间形式(14)可写成：

(15)

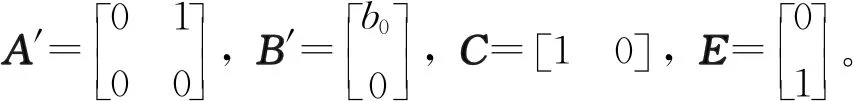
则为系统设计的LESO如下：

(16)

LESO的具体形式可写为：

(17)

它的输入为u(t)和y(t)，LESO中的2个系统状态z1和z2分别跟踪y和被扩张的状态f，且观测器带宽ω0是唯一可调参数。

2.3 线性状态误差反馈控制律

线性状态误差反馈控制律是对LESO产生的状态误差量进行反馈来构成线性状态误差反馈环节，它和LESO对总扰动的补偿量组合来构成系统控制量。LSEF把非线性反馈用状态误差的线性加权来进行替代，使用扰动估计量的实时补偿项-z2/b0来消除静差。

通常在二阶及以上的系统中,LSEF环节采用比例-微分(PD)控制律，而对于一阶系统，由于没有对状态误差的微分进行观测，则采用下式所示P控制律。

(18)

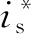
此处，u0是系统控制量，但还没有加入对扰动估计值z2的补偿。考虑到对扰动的补偿，在上文已设计的二阶线性扩张状态观测器的基础上，最终的控制量可取为：

(19)

由以上控制律和控制量的选择，设计如图4所示的线性自抗扰控制器。

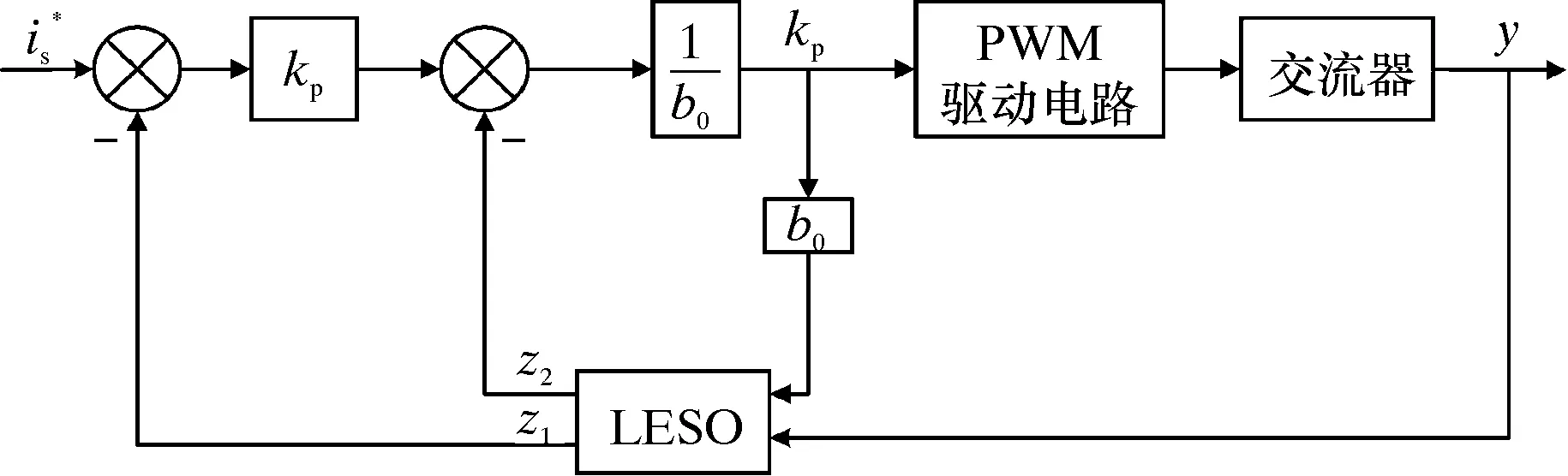
图4 线性自抗扰控制器Fig.4 Linear active disturbance rejection controller

线性自抗扰控制器中参数如下：增益系数kp，观测器带宽ω0，扰动补偿因子b0。对于已经建立模型的系统b0为已知，在控制器参数整定时可以先确定ω0，再根据实际控制效果调整并选择合适的kp。LADRC控制模型如下：

(20)

其中：

β1=2ω0

(21)

(22)

kp=ωc

(23)

2.4 系统控制结构

APF系统的控制器设计可以看作由一个直流侧电压控制外环和一个电流控制内环构成。外环通过一个PI控制器对直流侧电压进行控制，并获得电源电流的给定值。内环的电流控制采用LADRC，在得到控制量后由脉宽调制(PWM)环节实现对APF的控制。系统控制结构框图如图5所示。

图5 APF控制结构框图Fig.5 APF control block diagram

3 对比仿真分析

为验证上述方法的有效性和可行性，依据图1所示的电动钻机电网APF结构，在Matlab/Simulink环境下建立仿真模型。建模时主电路元件参数取值如下：线电压为380 V，频率50 Hz，输出电感1 mH，直流侧电容4 mF，直流侧电压参考值设置800 V；线性自抗扰控制器中ω0=150，kp=20，b0=2 350。

非线性负载为带阻感负载的三相不可控整流电路，设置2组不同参数的非线性负载以验证控制策略的适应性：A负载的电阻为10 Ω，电感为2 mH；B负载的电阻为15 Ω，电感为4 mH。

3.1 稳态性能对比分析

图6为负载电流和频谱分析图。从图6可看出，负载电流中含有较高的谐波电流，主要以3、5、7次谐波为主。A负载的谐波总畸变率(THD)达到23.77%，B负载的THD达到29.84%，都远超过了国家标准规定的5%。

图6 负载电流和频谱分析Fig.6 Command signal and compensation current waveform

图7 指令信号和补偿电流波形Fig.7 Grid current waveform and spectrum analysis after PID compensation

图8为采用PID控制补偿后的负载电流波形及频谱分析图。由图8可以看出，补偿后A负载的THD为4.52%，符合国家标准规定的要求，但补偿后B负载的THD为6.09%，未达到国家标准规定的要求。

图9为采用LADRC控制补偿后的负载电流波形及频谱分析。

由图9可以看出， A、B负载补偿后的THD分别为1.04%和3.23%，均符合国家标准规定的要求，验证了LADRC比PID具有更好的滤波性能。

图9 LADRC补偿后负载电流波形和频谱分析Fig.9 Load current waveform and spectrum analysis after LADRC compensation

3.2 抗扰性能对比分析

为验证LADRC的抗扰性能强于PID，将突加负载作为系统扰动。在t=0.1 s时接入负载，通过观察突变时的电流波形回到稳态的时间，对比分析2种控制器的抗扰性能。图10为突加负载时的负载电流波形。图11a、图11b分别为PID和LADRC控制时补偿后的网侧电流波形。

由图11可知，采用PID控制时系统在不同负载下突变后经过约0.04 s均能恢复到稳态，而采用LADRC控制时不同负载下的系统经过约0.02 s均能恢复到稳态，验证了在APF系统中LADRC比PID具有更强的抗扰性能。

图10 突加负载后负载电流波形Fig.10 Load current waveform after sudden load

图11 系统突加负载后的网侧电流波形Fig.11 Grid-side current waveform after the system is suddenly loaded

4 结束语

针对电动钻机电网中传统PID控制时谐波补偿精度低和动态响应速度慢的缺点，设计了一种线性自抗扰控制器用于APF的电流跟踪控制，对不同负载下分别采用PID与LADRC控制时APF的跟踪性能、滤波性能及抗扰性能进行分析。通过将不同负载下2种控制策略的仿真结果对比，验证了在LADRC控制下APF的补偿电流能更实时地跟踪指令信号、具有更好的滤波性能以及具有更强的抗扰性能。因此，LADRC相比于PID控制更适合APF控制，具有较高的工程应用价值。