聚焦二次函数中已知最值求参问题
2021-05-18山东省威海市第二中学264200宗香荣
山东省威海市第二中学 (264200) 宗香荣
二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动,不论哪种类型,解决问题的关键是讨论对称轴与所给区间的关系.研究已知最值求参数问题,就是要依据二次函数图象的对称轴与给定区间的变化关系进行分析,再通过分类讨论确定取最值点,然后建立等式求出参数的值.下面根据几个典型特题例的分析,揭示此类问题的求解方案,供读者朋友参考.
一、定轴、定区间、定开口方向
例1 已知f(x)=x2+2x+a2-1在闭区间[0,1]上有最小值为1,求a的值.
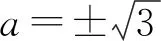
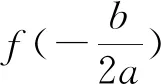
二、定轴、定区间、开口方向不确定
例2 已知f(x)=ax2+2ax+1在[-3,2]上有最大值4,求a的值.

评注:由于二次函数的开口方向的不同,则何时取得最值也可能是不同的,我们必须通过研究对应的函数图像确定取最值的情况,再列式求解.
三、定区间、定开口方向而对称轴位置变化
例3 已知函数f(x)=-x2+2ax+1-a在区间[0,1]上有最大值2,求a的值.
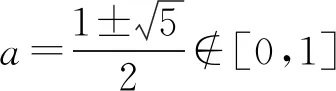
评注:由于抛物线的对称轴是沿x轴左右平移的,所以只要分别讨论对称轴在定区间的两侧和中间等三种情况就可以了.此类问题中需要注意,通过列式解方程得到的参数值要与此时参数所在的对应范围进行比较后才能确定,否则容易出现增解.
四、定区间、对称轴与开口方向都不确定
例4 已知函数f(x)=ax2-2x在区间[0,1]上有最小值为-1,求a的值.
解析:(1)当a=0时,f(x)=-2x在[0,1]上单调递减,所以[f(x)]min=f(1)=-2,所以a=0不满足题意,舍去.

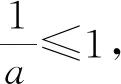
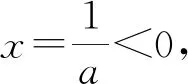
评注:区间定、对称轴与开口方向都不确定的求函数最值问题是一个非常复杂的问题,一般情况下,要分开口方向和对称轴两级讨论.由于此题中的一次项系数为常数,没有常数项,所以很多步骤都省略了,若不是如此,就难以承受了.
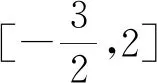
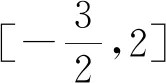
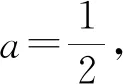
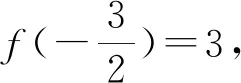
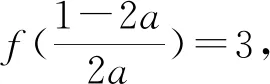
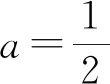
评注:本题如果采用例4的方法,那是困难重重的,而本解法是从整体上去考虑问题,这样就大大简化了解题难度,所以在遇到困难时,换一种想法,跳出原来圈子外重新思考问题,可能会有惊喜出现.
五、定二次函数,而区间的一端在动
例6 已知函数y=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,求m的取值范围.
解析:由于二次函数y=x2-2x+3图象的对称轴为x=1.当m<1时,y=f(x)在[0,m]上为减函数.所以ymax=f(0)=3,ymin=f(m)=m2-2m+3=2.则m=1,无解.当1≤m≤2时,ymin=f(1)=12-2×1=3=2,ymax=f(0)=3.当m>2时,ymax=f(m)=m2-2m+3=3,所以m=0或m=2,无解.所以m的取值范围1≤m≤2.
评注:由于只有一个变参数,所以难度不大,只要我们通过分析函数图像,抓住何时取最大或最小值的情况,就不会出现什么意外的.
六、定二次函数,区间长度定,而两端在动
例7 设函数f(x)=x2-2x+2,若x∈[t,t+1],t∈R,求函数f(x)的最小值g(t)的最小值.
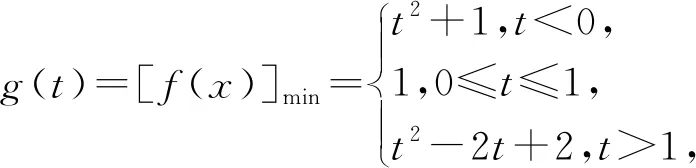
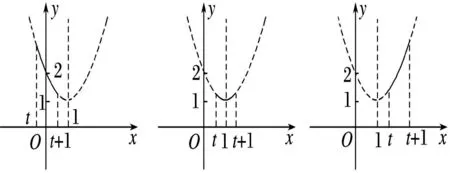
图1 图2 图3
评注:由于区间的长度不变,所以就可以看成是一个线段在x轴上滑动,然后通过研究函数图像在此变区间内的单调情况确定其最值.本题通过对区间端点关于抛物线顶点位置的讨论,利用函数图象确定函数在所对应的区间内单调性,顺利找到了最小值,这也是解决二次函数的最值问题的通法.
虽然求二次函数的最值有通法,但在各类不同类型的题目中又有题目本身的特点,所以在具体解题过程中,要在通法的基础上抓住特点,建立符合自身条件的解题方案,这样就是简化解题、精确思考的优良思维品质的体现.
