一道复旦大学自主招生试题的解法探究

重庆市中山外国语学校 (404500) 廖双平

二元函数最值问题一直是各高校自主招生考试中的重点考查对象，也是学生学习的难点之一，因其灵活多变，备受命题者的关注.本文对2020年复旦大学自招试题的一道给定条件的二元函数最值问题的解法进行了深入的探究，希望给大家启发.

1.试题呈现与分析

(2020年复旦大学自主招生试题第3题)已知x2+2xy=1，求x2+y2的最小值.

试题分析：题目结构清晰，形式简洁，以函数为背景，主要考查二元函数的最值问题，突出考查学生逻辑推理和运算求解方面的能力，试题的思维过程和运算过程体现了能力立意的命题思想，较好地检测学生的数学素养和学习潜能.

2.解法探究

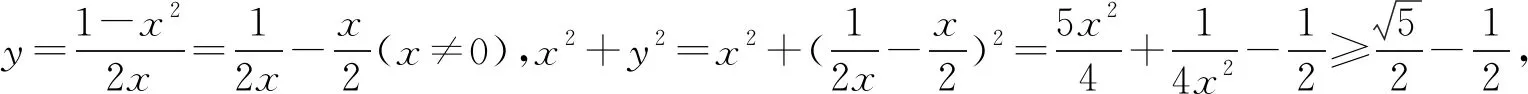
评注：本解法是参考答案给出的方法， 采用代入消元法解决最值问题，思路清晰，解法自然，是解决此类问题的常规方法，但是运算量稍大.

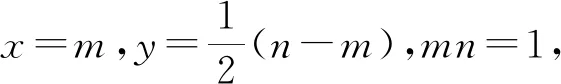
评注:“化陌生为熟悉”是数学中处理问题的常用方法，体现了数学转化思想，换元法是解此类最值问题的常用方法之一.

由于所给式子具有齐次式特点，所以有下面两种解法.

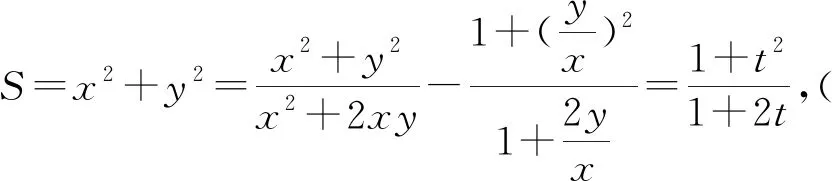
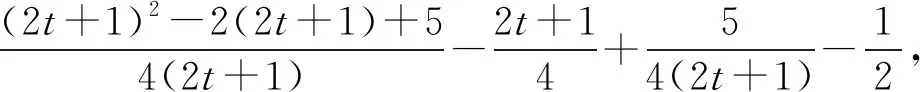
评注：将x2+2xy看成一个整体，巧妙借助“1”的代换将所求表达式转化为齐次式并换元，结合均值不等式求解，技巧性强，需要学生对该类问题有一定的知识储备.

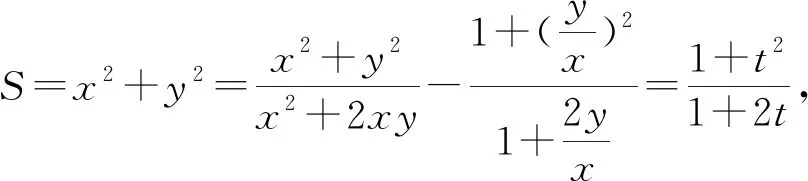
评注：解法4采用判别式法，对于类似于这种二元最值问题，判别式法也是一种通法，而且运算量不大，二元转化为一元的过程也比较自然.

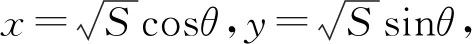
评注：解法5是采用三角换元，借助三角函数的有界性确定变量的最值，极大简化了运算过程.

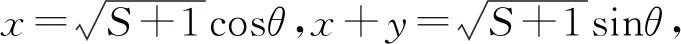
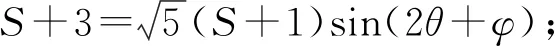
评注：解法6本质上同解法5一样，根据题目条件进行三角换元再结合三角函数有界性求解.

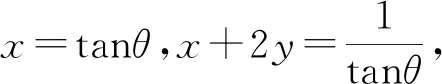
评注：解法7本质上与解法3是一致，利用三角换元后借助基本不等式法.

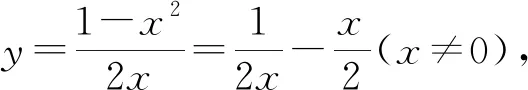
评注：多元函数最值问题可以通过消元，最终变为一元函数最值问题来处理，而 “导数法”则是求一元函数最值的通用解法,具有普遍性.

3.进一步的运用

例2 若x2+3xy+2y2=1，求x2+y2的最小值.

分析：此题为二元条件最值问题，求解较为麻烦.通过部分换元可以得到较为简便的解法.

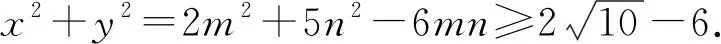
例3 已知x2+xy+2y2=1，求x2-3xy+2y2的取值范围.

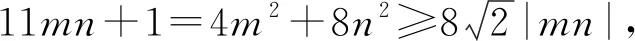
例4 若6x2+6xy+4y2-1=0求x2-y2的最大值.

例5 在正实数范围内，xy(x-y)=4求x+y的最小值.

分析：此题解法较多，常见的方法有消元，换元，整体代换等.根据试题特点，此题用整体代换较为简单.

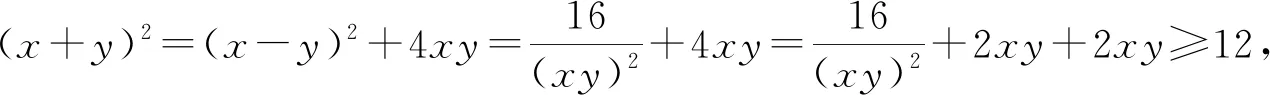
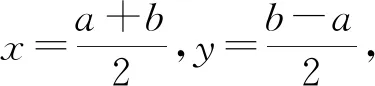
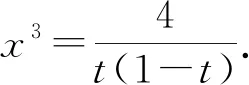
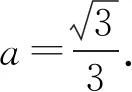
对于多元条件下的函数最值问题，不论是竞赛、自主招生考、高考还是各地的模似考，一直是考试中命题的热点；由于这类问题求解时，所要求的分析能力较强，涉及到的数学思想方法较多，变形的技巧性较高，其重点关注学生对基本知识、基本技能的理解和掌握及灵活运用，着重提升学生思维的深刻性、灵活性、创造性，通过多视角透析题目条件，探寻多角度解法，提炼解题策略.