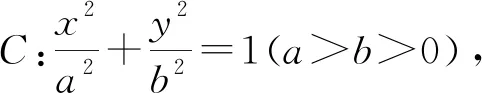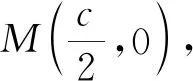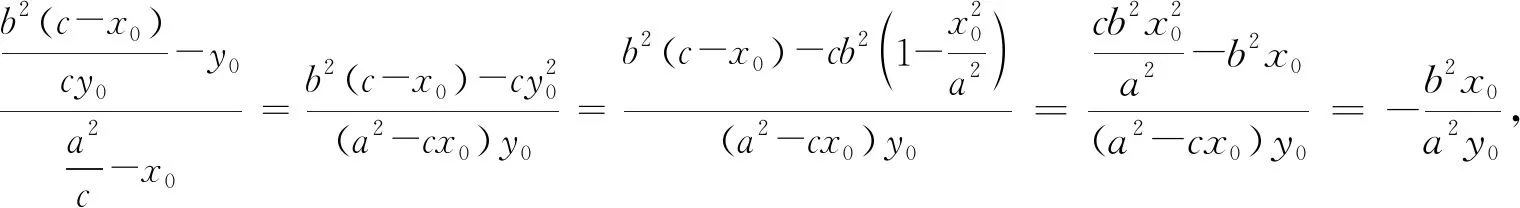一道质检题的解析与引申

福建省龙岩市高级中学 (364000) 林金荣

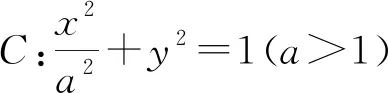
(Ⅰ)求C的方程；

(Ⅱ)过点F2引PF2的垂线交直线l:x=2于点Q，试判断直线PQ是否与C有其他公共点？说明理由.

本题源自2010年安徽卷理科19题及2013年山东卷理科压轴题，它以椭圆的几何性质为基本素材，为考生创设了一个陌生情境，旨在考查学生的逻辑思维能力、运算求解能力，以及应用解析几何思想方法分析问题解决问题的能力. 本题第(Ⅰ)小题，考查椭圆之焦点三角形的基本计算，考查学生在直角三角形的情形，内角平分线的处置办法．本小题入口较宽，方法多种多样，注意到角是一个轴对称图形，角与等腰三角形之间具有天然的内在联系，以及角平分线的诸多几何性质等，学生可以根据自己的情况，用自己熟悉的方法入手，比如：几何方法的分割；直接套用正余弦定理的三角方法；机械的代数方法等，以充分发挥自己的长处，如果方法得当且运用得比较灵活，那么将省时省力，为完成后面的题目创造有利条件．

一、几何方法

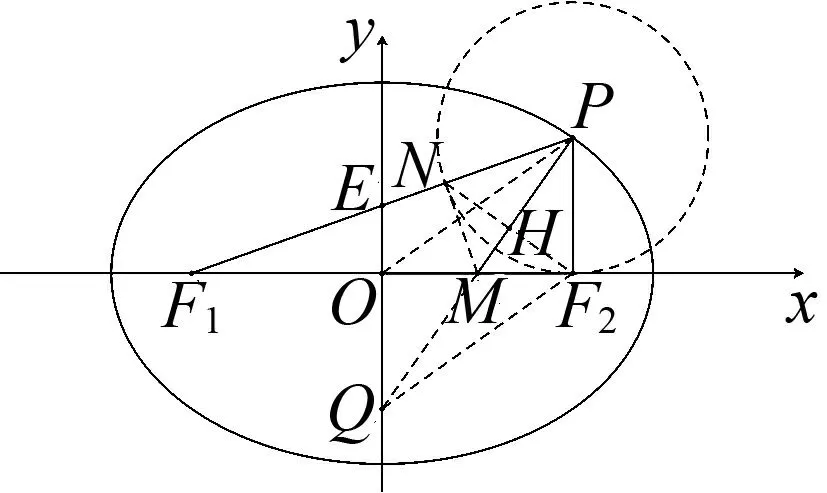
图1

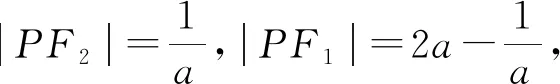
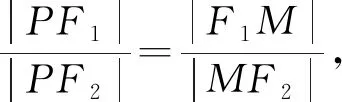
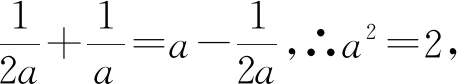
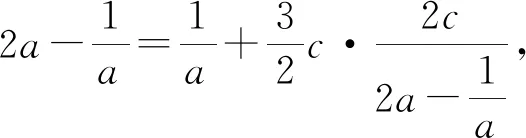
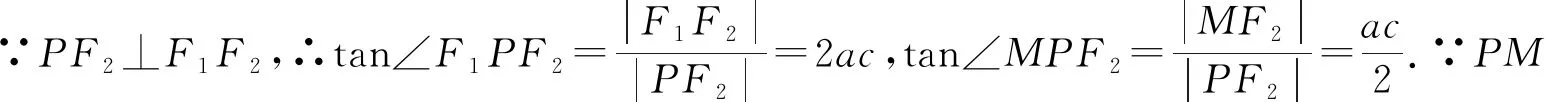
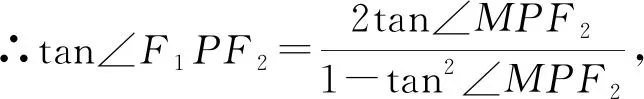
二、三角方法

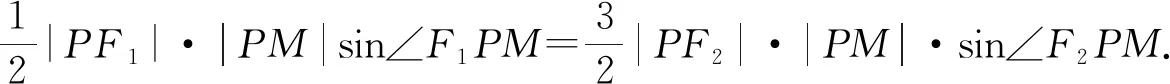
解法六：(正弦定理)在△PMF1与△PMF2中，根据正弦定理，化简整理可得|PF1|=3|PF2|，以下同解1.

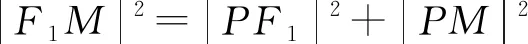
三、代数方法

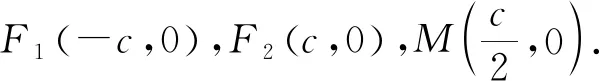
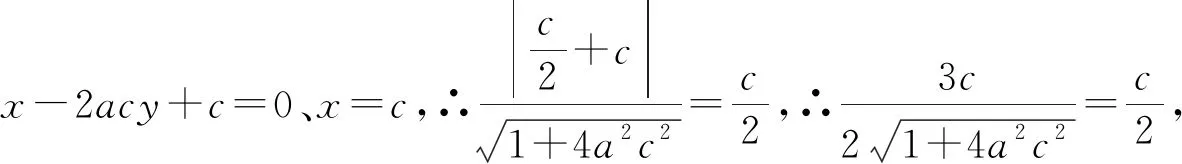
解法9：(倒角公式)∵PM平分∠F1PF2，

∴tan∠F1PM=tan∠MPF2，根据倒角公式，

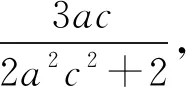
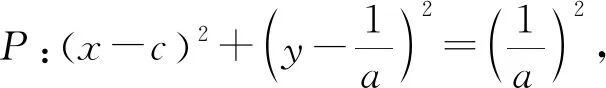
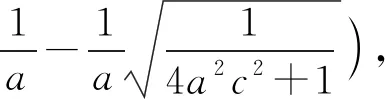
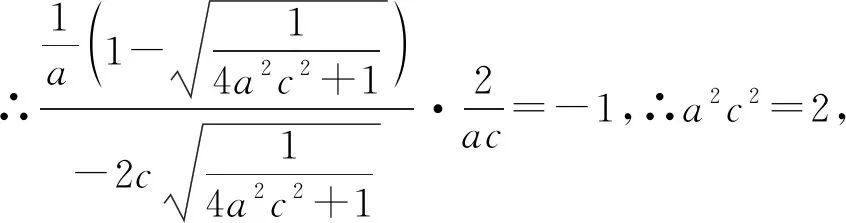
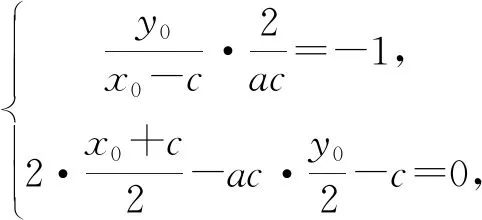
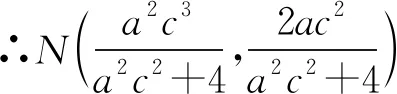
∴a2c2=2，以下同解法4.

评注：求解三角形问题，是高中数学的基本计算之一，直接运用三角方法的题目占了很大地盘，但当直接应用正弦定理、余弦定理、三角形的面积公式求解它遇到一定困难的时候，我们不妨换一个角度想一想，通过添设辅助线并联想平面几何的知识对图形进行处理(比如解一至解三)；或者运用数形结合的思想方法去分析(比如解八、解九)，也许思路更加自然，能寻找到一条更加简捷合理的途径．

本题第(Ⅱ)小题，揭示了与椭圆焦点、准线，以及切线息息相关的一个几何性质，内涵十分丰富，主要考查直线与圆锥曲线的位置关系，考查学生的运算求解能力、推理论证能力，考查函数与方程思想、转化与化归思想等.

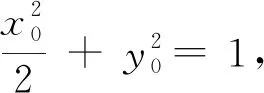
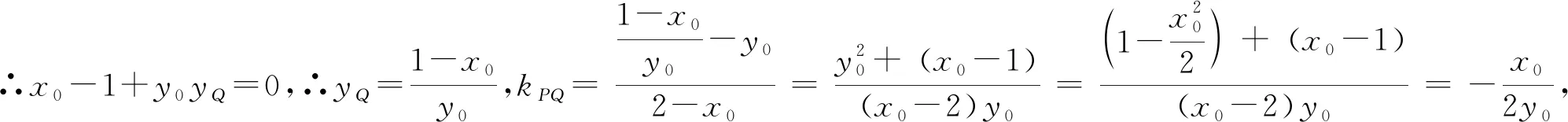
评注：研究直线与圆锥曲线的位置关系，基本的途径就是将直线方程与圆锥曲线方程联立，消去y(或x)，得到关于x(或y)的方程，运用判别式等作进一步讨论．

以下，我们将上述题目引申为更一般的情形．