一道与外心有关的向量题的解法与变式*

重庆市长寿中学校 (401220) 田 鹏

平面向量是高考考查的重要知识，其中与三角形的重心、垂心、内心、外心综合考查的题目屡见不鲜.本文从多角度探究一道与外心有关的向量题，以期和同行们交流.

1 题目呈现

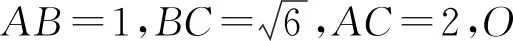
本题是课时作业上的一道习题，具有题干简洁，问题明了的特征.在讲评该题时，多数学生表示一时难以找到突破口，笔者课后对本题进行了深入的探究，发现是一道综合考查学生逻辑推理、数学运算等数学学科核心素养难得的好题，其解题过程不乏处处彰显数学思想.为了解题方便，在此先给出两个引理.

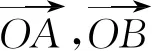
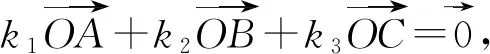
2 解法探究

本题中的△ABC是完全确定的，外心O是△ABC三边的中垂线的交点，故O在△ABC三边上的投影为三边的中点，且满足OA=OB=OC，如果从这些性质入手，建立x,y的两个方程，则问题迎刃而解，所以有以下几种解法.

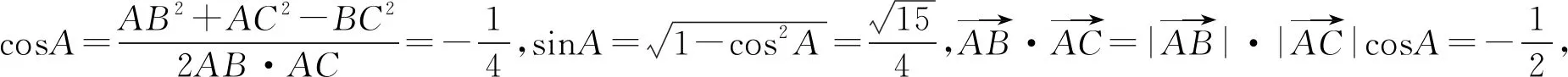
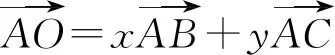
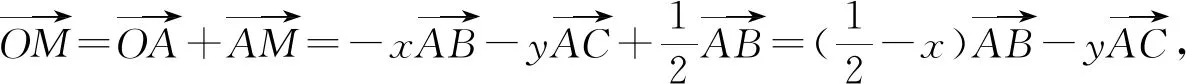
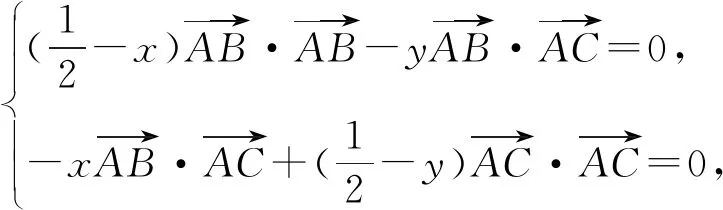
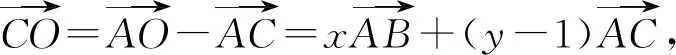
以上四种解法大同小异，充分利用了外心的各种性质，建立起了x,y的两个方程，通过解方程的思想求出了答案，那么此题还有其他解法吗？还有没有建立x,y关系式的其他方法呢？经过继续探究，发现了另外两种建立x,y关系式的方法.

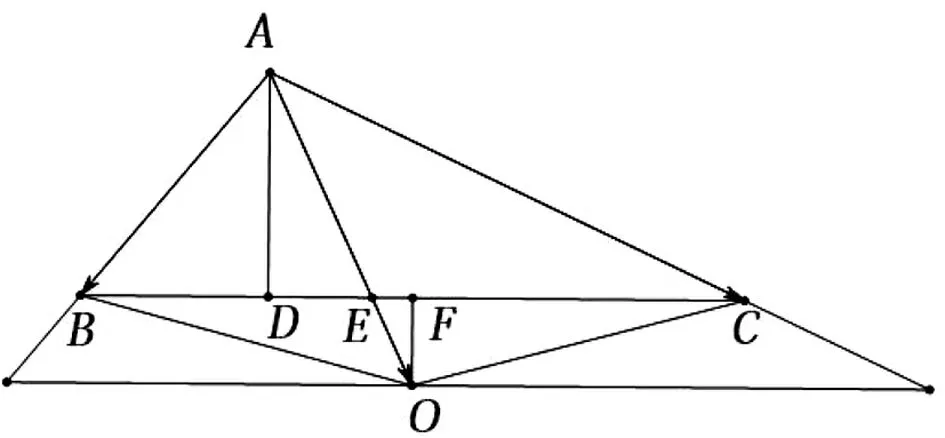
图1

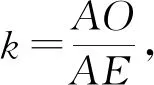
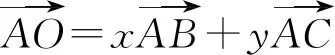
解法五和解法六从另一角度对该问题进行了分析，具有很大教育价值，特别是对基础较好的学生更应该培养他们分析问题，提出问题，解决问题的能力.问题是灵魂，以问题为载体，不断加强学生的创新思维意识，培养举一反三的能力，这也是新课程改革重要目标之一.那么还有没有解决这道题的其他方法呢？上面六种解法都是以建立x,y的方程为核心，充分体现了方程思想的重要作用.通过探究，发现还可以建立坐标系或运用向量的基本运算这两种方法.

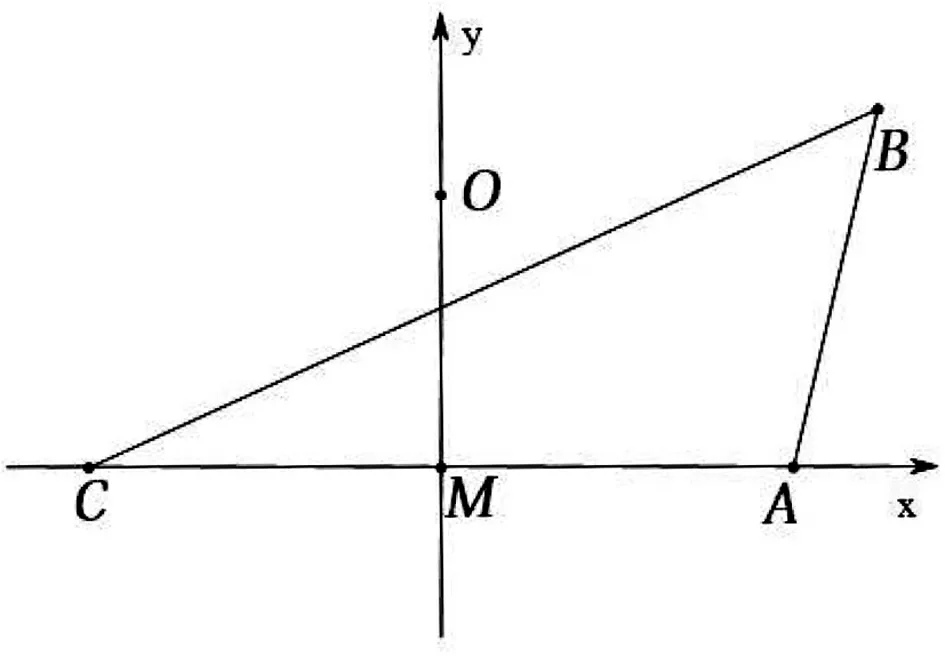
图2

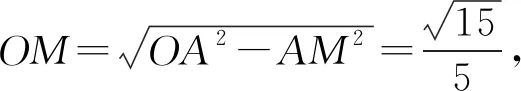
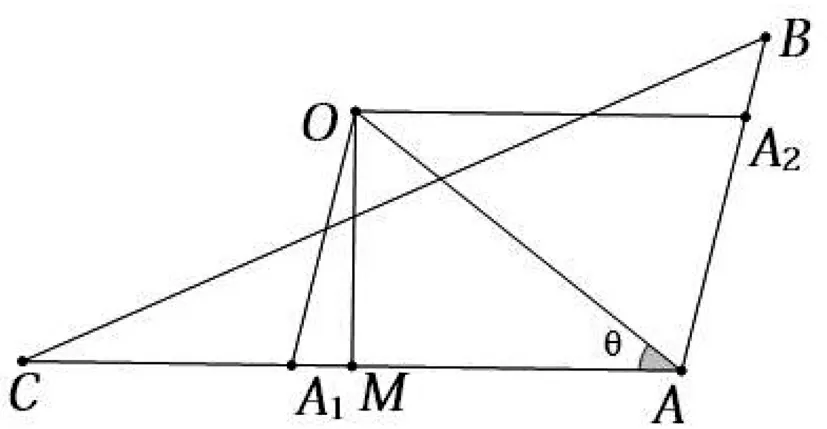
图3

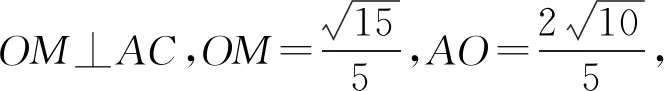
解法七和解法八本质是一样的，都利用了向量的基本运算.解法七用了向量的坐标运算，解法八用到了向量的平行四边形法则.这两种方法对加深学生对向量运算的理解大有好处.如何建立坐标系？如何利用平行四边形法则来分解向量，如何把复杂问题转化为简单问题？这是落实学生数学学科核心素养的重要途径之一.

3 变式探究

学会解一道题不是最重要的，而是通过解一道题，学会一类题的解法.把原题所考查的知识点进行梳理，全方位、多角度去剖析问题.通过改变题目的条件或者结论，就可以得到与原题相关的一些变式题，研究一下这些变式题与原题在解法上的区别，就会有收获.本着以题育人，以题培养学生数学核心素养的目的，对该题作出以下变式：

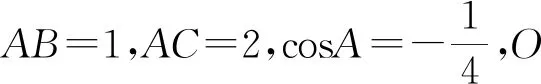
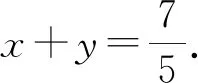
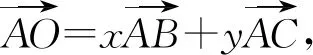
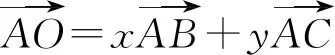
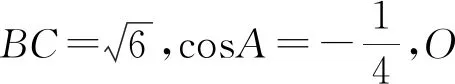
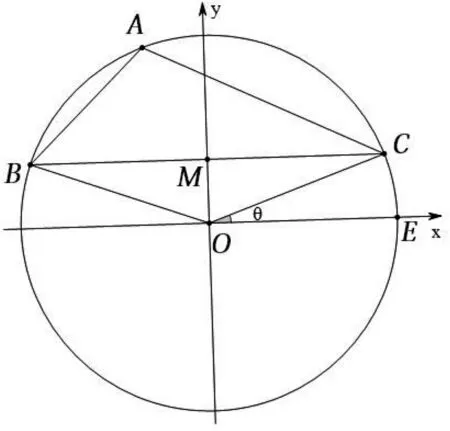
图4

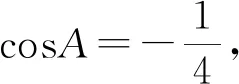
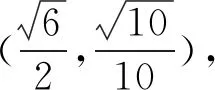
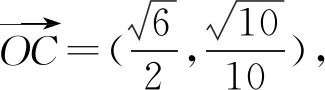
以上变式都采用了其中一种方法，当然也可以用其他方法，读者可以尝试一下.通过一题多变，一题多解，学生的发散思维得到锻炼，提高了分析问题，提出问题，解决问题的能力.

4 小结

新的高考改革，是从知识立意到能力立意，再到以学科核心素养为导向的深层次改革，不仅要求学生会解题，更应该要求学生创新，能够利用已有的知识解决数学内部，乃至自然生活中的问题，学会用数学的眼光观察现实世界，用数学的思维分析现实世界，用数学的语言表达现实世界.这条路任重而道远，需要每一位教育工作者不懈地努力.在平时的教学中，提倡一题多解，一题多变，多题归一的教学模式，有利于提升学生的思维品质，有利于培养学生数学核心素养.