数学教学中要重视数据处理能力的培养*

广东省中山市龙山中学 (528471) 李云章

数据处理能力是现代社会发展中对学生提出的一项新要求．《普通高中数学课程标准(实验)》对数学能力的要求有所提高,增加了数据处理能力．数据处理能力是指会收集、整理、分析数据,能从大量数据中抽取对研究问题有用的信息, 从而作出正确的判断与决策的能力．

每一个数学问题都是由数据组成的,提高数据处理能力,能够帮助学生找出正确的解题思路．完善的数据处理能力包含多个方面的内容,它要求学生在正确审题的基础上能运用相关的数学方法分析数据，能利用图象和数字等整合数据，同时能够熟练应用计算机等辅助工具处理数据，并能够通过计算准确得出结果等．数据处理能力不只是一般的数据统计问题，它在高中数学的很多分支上都体现出来，能够对题目中所给的数据由识别、理解，到筛选、归类，再到运用、发挥作用，就有可能比较完美的解决这道题．下面分类举例介绍数据处理能力的体现和要求，供读者朋友参考．

一、统计问题中的数据处理

统计问题在小学、初中、高中的教材都有，而高中的要求更为具体，涉及的内容也比较多，是对数据处理能力的培养的集中体现之一．

例1 某个班级的四个小组的人数分别为12、12、x、10，若已知这组数据的中位数与平均数相等且有一个众数，试求这组数据的平均数．

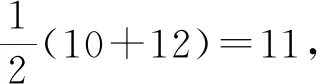
评注：本题对平均数、中位数、众数的概念进行了考查，是较为简单的问题，但如果对概念理解不清，数据处理能力不强，尤其是没有分类，就会发生错误．

二、立体几何问题中的数据处理

虽然说立体几何问题是与几何图形相关，但有的题目中含有角的大小的计算，距离的计算和面积、体积的计算，也有的需要通过数据处理来判断线面关系．

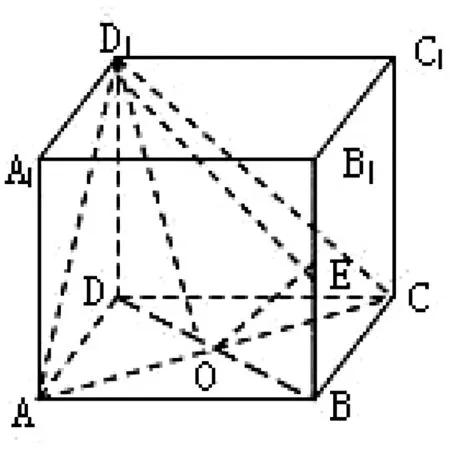
图1

例2 如图1，在正方体ABCD-A1B1C1D1中，E是BB1的中点，O是底面ABCD的中心.求证：OE⊥平面ACD1.

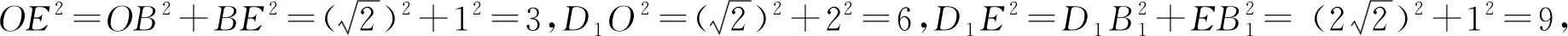
评注：正方体和正四面体等是一些特殊的几何体，有许多的数量关系，应该利用好这一点．本题中虽然没有给出具体数据，但通过赋值，然后再计算处理，使问题获得解决．

三、函数问题中的数据处理

一些函数问题的题目中，会出现含有一定规律的数据出现，通过对这些数据变形和化归处理，可以挖出当中所隐含的条件，揭示其中规律．

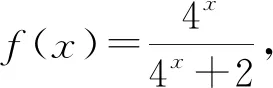
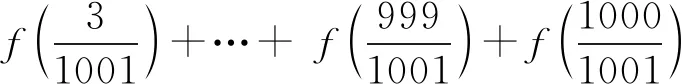
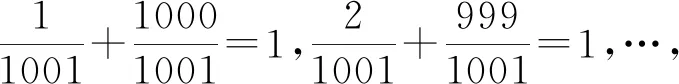
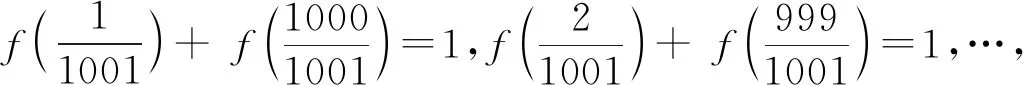
评注：有些给出的数据中隐含着等式关系，它就提示了该数学问题的本质，挖掘出这些隐含的等式关系，就是我们解答此问题的切入点．

四、解析几何问题中的数据处理

一般的解析几问题都是与大量的字母运算有关，但有时对一些特殊数据进行分析处理，才能抓住机会巧妙破题．

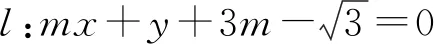
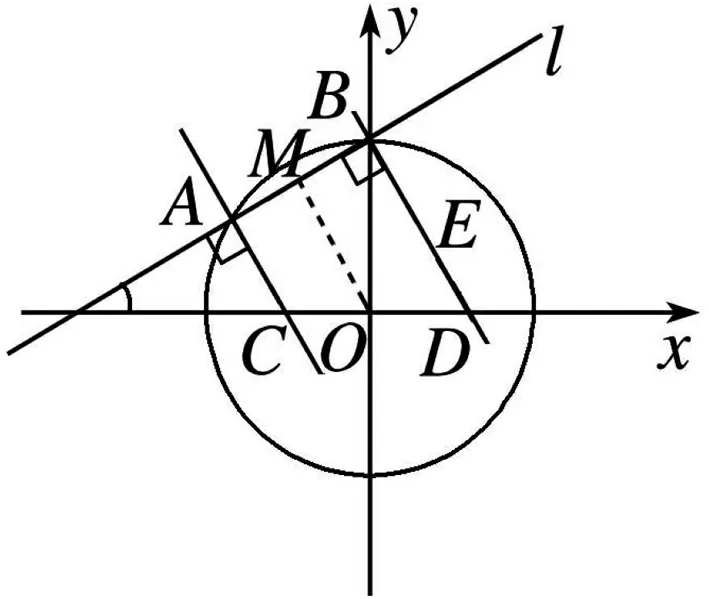
图2

解析：如图2，设AB的中点为M，由题意知，圆的半径

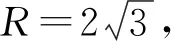
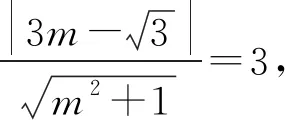
评注：在本题中抓住弦长的值分析出△OAB为等边三角形是成功解题的重要一环，而后续解题就是围绕如何求C,D两点坐标进行的努力，也是比较容易达到解题目的的．

五、数列问题中的数据处理

数列中的数据比较精致，某一个数据有时都能起很大作用，如数列的下标、数列中的项和某一些表达式中的数据，我们不可轻视它的作用．

例5 在等差数列{an}中，若前n项和记为Sn，已知a3=12，S12>0，S13<0，当n为何值时，Sn最大？

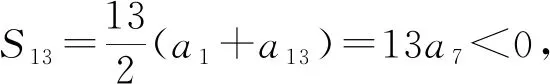
评注：本题中通过分析条件S12>0，S13<0，得出相邻两项a6>0，a7<0，虽然做的是数列下标的数字游戏，但问题就在这些下标变化中解决了．

六、基本不等式问题的数据处理

用基本不等式解决最值问题是高频率的题目，其中题目条件的不同，解题方法也多种多样，而利用数字“1”就是常用方法，必须熟练掌握．

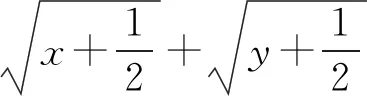
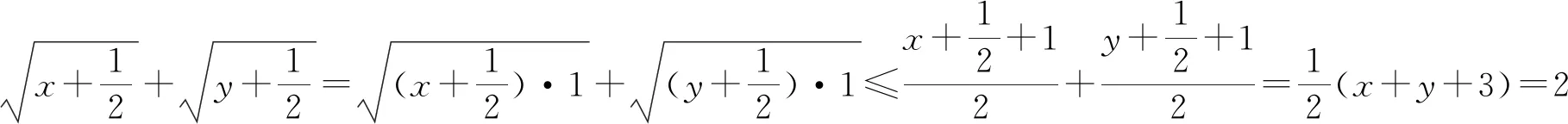
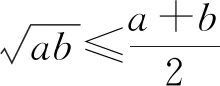
七、三角函数问题中的数据处理

三角函数中对角的数值处理比较多，要善于发现和运用某些特殊角的关系，将问题化归分类解决．

例7 求(1+tan1°)(1+tan2°)(1+tan3°)…(1+tan44°)的值．

评注：通过观察给出角的特点，寻找熟悉的三角公式的模型是分析题意的要点，灵活地将tanα+tanβ转化为tanαtanβ的关系，这样就为后续解题排除了障碍．

通过以上各例的分析求解我们可以知道，正确有效的数据处理有时是解决问题的关键，我们必须正视发展数据处理能力在高中数学中的重要性，而作为教学人员必须提醒同学们，在做题时严肃对待每一个数据的处理，通过足量的练习，就能使数据处理能力得到提高．