一道高考压轴小题的多解探究与反思
2021-05-18云南大学附属中学星耀学校650092
云南大学附属中学星耀学校 (650092) 黄 波
一、试题呈现
(2020年全国Ⅲ卷理12)已知55<84,134<85,设a=log53,b=log85,c=log138,则( ).
A.a C.b 本题结构较为简洁,以指对数为载体考查比大小问题,综合考查了指对数运算,比较大小的常规思路与方法,在考查通性通法的同时,对学生的数学思维能力提出了更高的要求,重点考查逻辑推理、直观想象、数学运算、数学建模等核心素养. 下面例举几种常用比较a,b大小关系的解法. 评析:比较两数的大小关系,作差法是常见的方法,属于通性通法.本题作差法容易想到,但使用基本不等式难易想到,此时就需要学生要有逻辑推理能力,并对对数运算法则要有深刻的认识.对数运算法则的基本法则是加法与减法,在乘积运算lg3·lg8时需考虑转化为加法与减法运算,需要构建加减与乘积的关系,进而联想到基本不等式.学生在学习过程中要重视逻辑推理思维能力的培养,步步要有章可循,有理可讲. 评析:比较两数的大小关系,作商法是常见的方法,属于通性通法.使用作商法也会涉及乘积运算lg3·lg8的处理,方法与上述相同. 解法四:(同倍放大)4a=log534=log581 评析:一般比较大小问题数与数差异性都不大,此题a,b的值差异很小,很难发现a,b的大小关系,为了容易发现差异性,可以同倍放大,直到具有明显差异并能够比较大小为止.所以,在两数值差异性较小的情况下,同倍放大是一种十分直观而又有效的方法. 评析:由于此题属于函数模块,所以解决问题要有函数的观点,函数的思想.比较大小要联想到函数的单调性,选择构造合适的函数,通过函数的单调性比较大小,该思想在2020年全国Ⅰ,Ⅱ卷中都有明显的体现.此题由于对数的底数和真数都在变,所以对数的底数与真数都要有自变量,但是通过观察很难构造函数,所以可以选择待定系数法,设f(x)=logkx+mx,利用两组数据求出解析式,由于无法直接判断函数的单调性,可以采取求导的方式判断函数的单调性,再通过单调性比较大小. 对于比较大小问题,常用的方法有作差法、作商法、直接法、间接法、二分法、同倍放大、构造函数等方法,要掌握住核心知识和知识的核心,同时需要重视同性通法,逻辑思维能力培养,加强数学运算,形成模块观点,数学学习要以提升数学思维能力为目标.二、试题分析
三、解法赏析

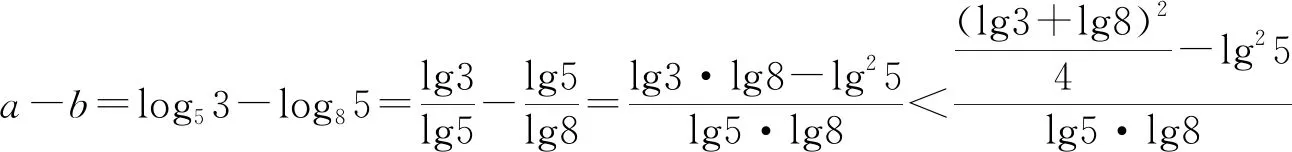
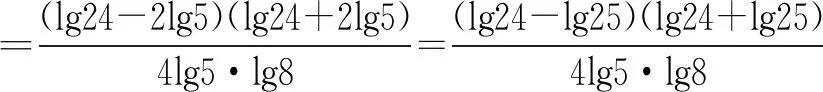
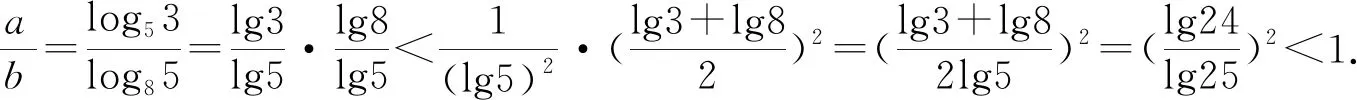
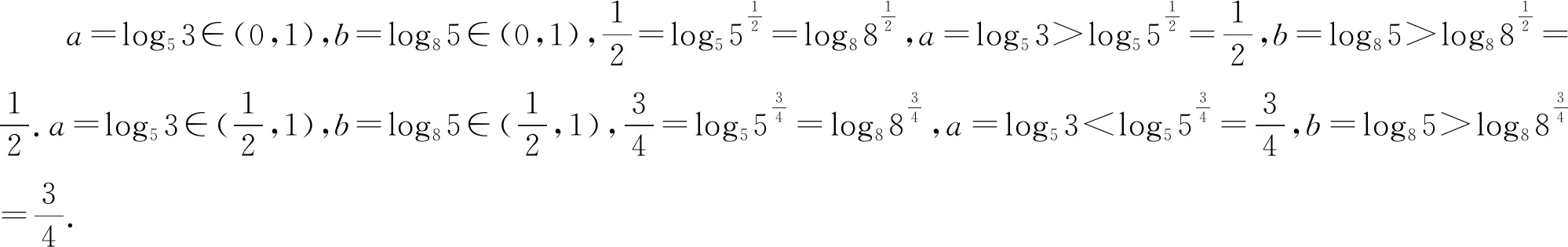
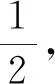
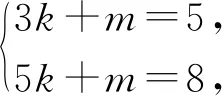
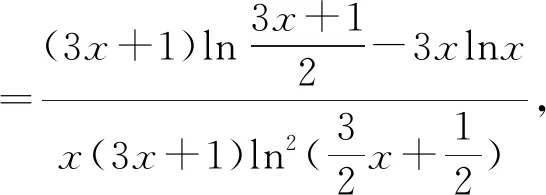
四、方法归纳
