排列组合中的分组分配问题微课教学

江西省南昌二中 (330013) 游 佳

排列组合的学习中经常遇到分组分配问题，尤其是部分均匀分组或分配问题．学生在求解这类问题时，常常会产生错误的解法：一是将其中均匀的部分重复计数；二是将分组、分配问题混淆．如何更好地处理这类问题，笔者进行了一堂微课教学.

引例1 疫情防控期间，我市某医院将5名援鄂医务工作者分配到3个不同的科室工作，每个科室至少分配一名医务工作者的方案种数为( ).

A.540 B.300 C.180 D.150

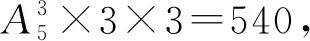
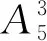
上述计数方法中是否出现了重复计数呢？我们不妨将5名医务工作者用a,b,c,d,e表示，三个不同的科室用A,B,C表示．举个例子,按上述计数方法，如果我们先安排了a,b,c分别去科室A,B,C，再安排d,e分别去科室A,B，则ad,be,c分别被安排在A,B,C三个不同的场馆．同理，如果先安排了d,e,c分别去科室A,B,C，再安排a,b分别去科室A,B，则da,be,c分别被安排在A,B,C三个不同的场馆．很明显这两种安排方案是相同的，也就是说在上面的计数方法中，对这种方案重复进行了计算．那怎样计算才可以避免重复呢？

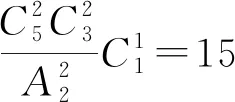
不难发现，这类问题是利用分步乘法计数原理，将第一步结果数乘以第二步结果数得到最终方法数的．学生的普遍错误原因在于混淆分组分配问题，并且对于分组问题中的部分均匀分组没有理解到位，在计算过程中往往会出现重复计数．

一般地，将n个不同的元素按某些条件分成k组，称为分组问题．分组问题有平均分组,不平均分组和部分平均分组三种情况．分组问题中的平均分组是无序的,各组方法数相乘时产生了顺序,故应消序(即除以平均组数的全排列);不平均分组是有序的,不需要消序;而部分平均分组应局部消序．

同样地，将n个不同的元素按某些条件分配给k个不同的对象，称为分配问题．分配问题有定向分配和不定向分配．

分组问题和分配问题是有区别的,前者组与组之间只要元素个数相同是不区分的,后者即使2组元素个数相同,但因对象不同,仍然是可区分的．对于后者一般我们按照先分组后排列(分配)的原则计数．所以求解排列组合综合问题为通常要遵循”先分组再分配”的原则,分组时应注意消去均匀部分的重复计数,定向分配问题可以理解为依次选择．

例1 甲，乙，丙三项任务，甲任务需2人承担，乙，丙各需1人承担，现从10人中选派4人承担这三项任务，则不同的选法种数有多少种？

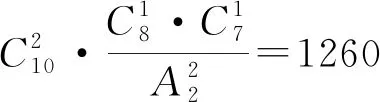
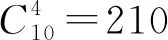
实际上，这是一道典型的排列组合计算问题，计算方法不只是以上两种．但求解时往往会将分组分配问题混为一谈，察觉不出其中的部分平均分问题，也容易出现重复计数的结果．主要原因是没有按照分类加法计数原理、分步乘法计数原理去分析问题特征，通常是几个组合数、排列数的叠加，不理解其中的实际意义，难以达到触类旁通．

例2 四个不同的小球放入编号为1，2，3，4的四个盒子中，恰有一个空盒的放法有多少种？

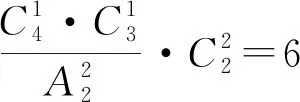
变式四个不同的小球放入编号为1，2，3，4的四个盒子中，恰有两个空盒的放法又有多少种？

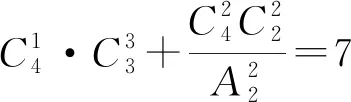
掌握了以上求解方法后，同学们在处理排列组合中此类问题时也就不易出错了.

巩固练习：设集合A={1，3，5，7，9}，B={0,2，4，6}，A为定义域，B为值域，则从集合A到集合B的不同函数有多少个？

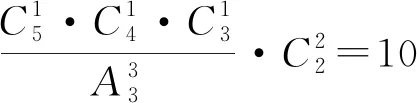
综上，笔者通过本微课对分组分配问题求解时采用“先分组再分配”求解的学习原则，教学时没有特别强调如何套用模型，而是引导学生在分析不同情境下如何按照分步乘法计数原理，理解这类问题的求解步骤，并在各步骤中进行准确分类．在此基础上再按照先分组后分配的原则准确分组，观察其中是否含有包含平均分组问题，从而考虑对均分的组数进行消序．由此达到触类旁通，灵活处理排列组合中的分法分配问题的目标.