掺杂硅波导实现可调谐红外激光输出

徐 浩，乔丽君，张明江，张建忠，王 涛，高少华

1)太原理工大学物理与光电工程学院，山西太原 030024；2)太原理工大学新型传感器与智能控制教育部与山西省重点实验室，山西太原，030024

近年来，高质量的中红外激光由于具有谱带灵敏度高、基频振动强且透射率比传统通信波段强的特点，在光网络、传感及检测等领域得到广泛应用. 量子级联激光器和级联拉曼激光器等中红外激光源存在低效率、高成本及调谐难等缺点，因此，利用非线性效应实现红外波长转换[1-2]成为研究热点. 采用聚合物AlGaAs和AlGaAs/Al2O3等二阶非线性[3]材料可以实现红外波长转换，但高损耗导致其转换效率较低. 利用三阶非线性效应也可以实现波长转换，如在高非线性光纤中通过简并四波混频效应可实现2 μm附近中红外波长输出[4]，但仍需要通过硅波导进一步扩大波长转换范围，具有结构复杂的缺点. 通过光子晶体光纤中受激拉曼散射效应也可实现高效波长转换[5]，但由于光纤弯曲半径减小会导致损耗增大，这种方法不利于集成化和小型化.

得益于互补金属氧化物半导体(complementary metal-oxide semiconductor, CMOS)平台的支持，硅光子技术日趋成熟．利用硅波导中的非线性效应可实现通信波段与中红外区的高效波长转换. 如利用双泵浦四波混频效应在多模硅波导中可实现70 nm的波长转换[6]；在高折射率掺杂二氧化硅波导中可实现100 nm的波长转换[7]. 对于通信波段到中红外波段的波长转换，受限于波长匹配等条件，三阶非线性效应的波长转换效率较低[8]. 硅材料的晶格对称性一旦被破坏，硅波导中也可实现二阶非线性效应. 如外加直流电场时，在多个泵浦波长下产生二次谐波[9]，或采用SiN等具有二阶非线性效应的材料涂附在硅波导表面形成复合硅基波导，从而产生诸如二次谐波等非线性效应[10-11]. 上述方法虽然推动了红外波长转换领域的进步，但仍难以实现波长可调谐输出.

本研究数值模拟掺杂硅波导中通信波段到中红外波段的波长调谐过程，通过掺杂粒子破坏硅材料对称性产生二阶非线性效应，并通过改变材料自由载流子浓度提高三阶非线性效应作用，导致硅波导中的非线性效应显著增强，实现由通信波段泵浦波长向中红外波长的调谐.

1 仿真模型

图1为掺杂波导的结构示意图. 选取导波层中的一段区域进行掺杂形成掺杂区，掺杂区长度为L， 激光信号由掺杂波导一端输入，经波导掺杂区的粒子随机散射作用，最终一部分光后向散射返回入射端，一部分光前向散射至波导另一端.

图1 掺杂波导结构示意图Fig.1 (Color online) Schematic diagram of doped waveguide structure

由于硅材料中的晶格对称性，其二阶极化系数一般为0，粒子掺杂导致对称性被破坏，会产生二次谐波等硅波导中较为常见的二阶非线性效应[12]. 硅材料中的简并四波混频通过非共振电子响应产生，强非线性效应产生时，简并四波混频效应占据主导作用，泵浦光、信号光及闲频光满足[13]

i(γpPp+2γpsPs+2γpiPi)Ap+

(1)

i(γsPs+2γspPp+2γsiPi)As+

(2)

i(γiPi+2γipPp+2γisPs)Ai+

(3)

ωp、ωs及ωi分别代表泵浦光、信号光及闲频光的频率， 对于简并四波混频， 满足2ωp=ωs+ωi. 在简并四波混频中，闲频光频率(ωi=2ωp-ωs)与泵浦光、信号光的频率相差较大，三阶非线性极化系数、线性损耗系数和模式重叠因子较为分散，特别是硅波导在如此宽的光谱范围内，其非线性效应会发生显著变化.

2 结果分析

硅基波导的总长度为500 μm，其中，导波层材料为Si；限制层材料为SiO2；掺杂材料为ZnO. 3种材料的光学参数如表1. 入射激光波长为1.55 μm，脉宽为10 fs. 基于硅波导中简并四波混频效应，采用时域有限差分法，计算从波导两端输出光信号的光谱特征，将能量归一化处理进行讨论分析.

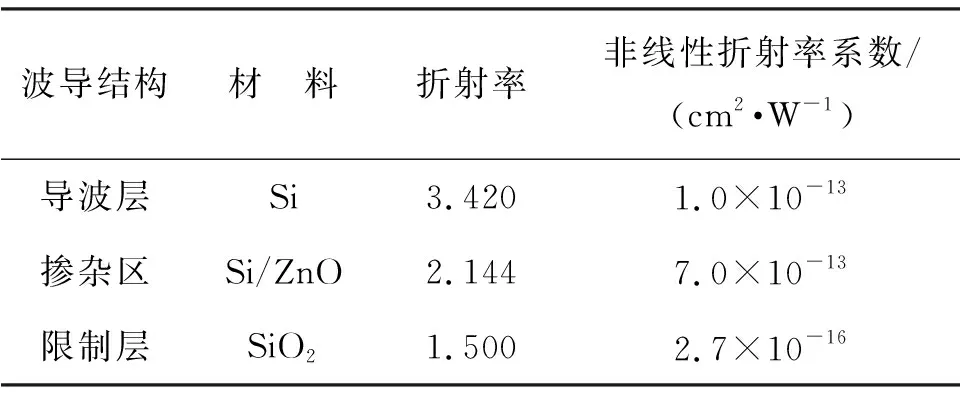
表1 波导材料光学参数

2.1 掺杂粒子尺寸为0.5 nm

采用离子注入法进行掺杂时，掺杂粒子尺寸小于纳米量级，设置粒子尺寸0.5 nm(本研究默认粒子形状为球体，以其直径代表粒子尺寸)，长度方向的粒子掺杂线密度100 μm-1. 得到不同掺杂长度对波导前向和后向散射光谱的影响，如图2和图3.

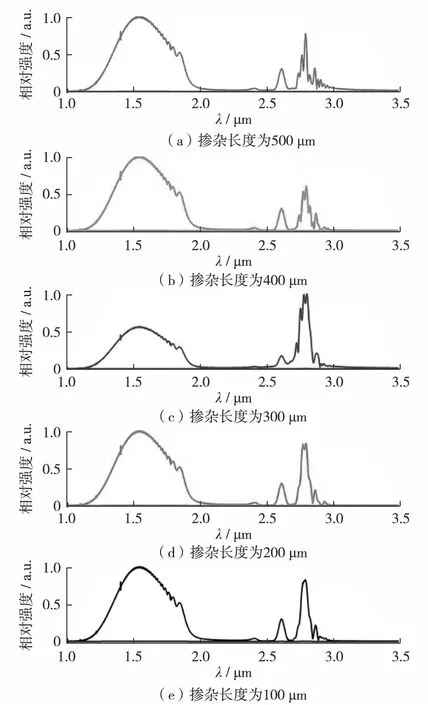
图2 掺杂粒子尺寸为0.5 nm时，不同掺杂长度下波导的前向散射光谱Fig.2 Forward scattering spectra of waveguides with different length of doping region and the size of doped particle 0.5 nm

图3 掺杂粒子尺寸为0.5 nm时，不同掺杂长度下波导的后向散射光谱Fig.3 Backward scattering spectra of waveguides with different length of doping region and the size of doped particle 0.5 nm

由图2可见，波长为2.62 μm的光是频率193 THz的泵浦波与272 THz光波发生简并四波混频效应而产生；随后2.62 μm的光与泵浦波、频率为187 THz光波通过四波混频效应产生2.77 μm的新频率成分；光波在2.77 μm处发生拉曼散射，在2.40 μm处产生较弱的反斯托克斯频移. 由图3的后向散射光谱图可见，2.62 μm及2.77 μm处的光成分与前向散射光的产生方式相同；当掺杂长度增加到300 μm时，波导中自由载流子吸收(free carrier absorption, FCA)和TPA效应明显，导致波长λ4处红移光和λ2处蓝移光的产生，其中，λ1是泵浦波与2.62 μm处光波通过简并四波混频产生；2.77 μm 的光波经过倍频产生λ3； 而后λ3与泵浦波长通过简并四波混频效应得到λ5.λ1—λ5依次为1.10、1.28、1.40、1.60及1.77 μm. 波导中自相位调制及自由载流子色散效应导致光谱宽度由44 THz展宽至约120 THz. 在前向散射谱中，由于四波混频效应的波长转换效率高于简并四波混频，因此，2.77 μm处的能量要高于2.66 μm处，当掺杂长度增加到300 μm时，非简并四波混频转换效率达到最低而后继续增加. 由后向散射光谱可见，当掺杂长度小于300 μm时，四波混频效应的波长转换效率比简并四波混频低；当掺杂长度超过300 μm时，简并四波混频的转换效率降低，导致2.66 μm处相对强度的降低；随着掺杂长度增加，波导中的二阶非线性效应在略增强后保持恒定(波长λ3). 由以上分析可知，在掺杂密度保持一定的情况下，对于尺寸为0.5 nm掺杂粒子，改变掺杂长度可以调节波长转换效率，当掺杂长度为300 μm时，前向输出光谱中2.77 μm处的能量最高.

图4 掺杂粒子尺寸为5 nm时，不同掺杂长度下波导的前向散射光谱Fig.4 Forward scattering spectra of waveguides with different length of doping region and the size of doped particle 5 nm

2.2 掺杂粒子尺寸为5 nm

在实际加工中，通过改变退火工艺条件，可以使粒子与缺陷结合，表现为掺杂粒子尺寸的增加. 因此，仿真中保持掺杂粒子密度为100 μm-1，掺杂粒子尺寸为5 nm. 图4和图5分别为不同掺杂长度下波导的前向和后向光谱. 可见，当掺杂密度一定时，掺杂波导中的非线性效应虽然有强弱变化，但波长转换范围保持1.55～2.77 μm不变. 随着掺杂区域长度变化，光谱在自由载流子色散作用下发生展宽，但中心峰值总体相差不大. 因此，当掺杂粒子尺寸为5 nm，保持掺杂密度固定时，掺杂区域长度对掺杂硅波导前后向的散射光谱并无明显影响.

图5 掺杂粒子尺寸为5 nm时，不同掺杂长度下波导的后向散射光谱Fig.5 Backward scattering spectra of waveguides with different length of doping region and the size of doped particle 5 nm

2.3 掺杂粒子数量的影响

保持波导掺杂区域长度为50 μm不变，当掺杂粒子尺寸为5 nm时，改变掺杂粒子数量n， 并对比掺杂前后波导的前向和后向散射谱，结果如图6. 由图6(a)可见，前向散射光谱中由于瑞利散射导致1.55 μm处出现明显波峰，随着掺杂粒子数量增加，泵浦信号透过率降低，导致瑞利散射峰明显下降；当n=1 000个时，在1.55 μm处形成反常色散，导致散射谱强度峰值降低. 由于四波混频效应，在波长2.70 μm附近出现了波长输出和较小范围的波长调谐. 对于未掺杂粒子的波导而言(图中黑实线)，在红外区附近还存在拉曼散射(左侧)和布里渊散射(右侧)，随着掺杂粒子数量增加非线性效应增强，这两种非弹性散射逐渐被抑制消失. 由于瑞利散射较强，在前向谱中无法探测到二阶非线性效应所产生的频率成分.由图6(b)可见，当未掺杂粒子时，λ1、λ3及λ5的产生机理与图3中相同. 增加掺杂粒子数量后，半导体材料晶格结构发生变化，在中红外区实现了225 nm的波长调谐，该峰值随着掺杂粒子数量的改变出现漂移，在n=5 000 个时，输出波长为2.85 μm的光信号. 由于掺杂区域长度固定，改变掺杂粒子数量等同于改变掺杂粒子密度. 因此，在掺杂密度一定时，调谐波长即可确定；通过改变掺杂区域长度，可以调节调谐质量，提高调谐波长的下转化效率. 应该注意的是，虽然未掺杂情况下的结果与图2和图3类似，并不表明掺杂粒子对波导的非线性效应无贡献，这是由于图2和图3中粒子尺寸较小所致.

硅波导中若存在多模激光信号，则会导致更复杂的非线性效应，本研究仿真中，前向和后向散射激光远场均为基模模式.

图6 掺杂区域长度固定时，不同掺杂粒子数量下波导的前向和后向散射光谱Fig.6 Forward and backward spectra of waveguides with different doping amounts when doped region length is fixed

结 语

本研究利用掺杂波导中非线性效应，实现从1.55 μm到中红外波段的可调谐波长转换，调谐范围达到225 nm，通过建模仿真研究掺杂粒子尺寸、掺杂长度及掺杂密度(即掺杂粒子数量)分别变化下，对波导非线性的影响. 根据仿真结果对比分析得出，掺杂密度对掺杂波导中的非线性效应影响显著. 仿真中使掺杂粒子数量由0个变为10 000个时，出现了0.225 μm的波长调谐范围. 根据本研究结果，可通过合理选择掺杂密度，实现不同的期望波长调谐范围，为后续研究提供基础及参考.