基于AP相似日选取与FISOA-RBF的短期负荷预测

于军琪，王佳丽，赵安军，解云飞，冉 彤，赵泽华

西安建筑科技大学建筑设备科学与工程学院，陕西西安 710055

大型公共建筑能耗大约占建筑总能耗的1/3，近年来随着社会经济的发展，该比例越来越大[1]，这令大型公共建筑能耗逐渐成为研究焦点．准确可靠的大型公共建筑用电短期负荷预测(short-term load forecasting, STLF)是建筑进行合理能源调度和节能优化运行的前提．与长期预测相比，时效性较高的STLF主要用于供配电的合理规划，受温差和湿度等突变因素影响大，属于动态非线性时间序列[2]．

近年来，许多学者提出了如人工神经网络(artificial neural network, ANN)、自回归(auto regressive, AR)、支持向量回归(support vector regression, SVR)及灰色模型(gray model, GM)等预测模型[2-6]．然而，AR模型根据平稳线性特征处理时间序列，难以适应动态非线性的STLF时间序列；SVR更适合小样本数据，在面对大规模训练样本时，收敛速度慢；GM适用于单调变化的时间序列，难以预测波动较大的时间序列[7]．针对逆传播(back propagation, BP)神经网络存在收敛速度慢、易陷入局部极小值的不足[8]，径向基(radial basis function, RBF)神经网络因只有一个隐层所以具有收敛速度快的特点，被广泛用于不同的实际需求中[9-10]．选取合适的网络参数是提高RBF性能的有效手段[11]．回立川等[12]采用近邻传播算法获取RBF神经网络的中心矢量，提高了网络的训练精度，但算法收敛速度慢．翟莹莹等[13]通过改进k-means++算法和方差度量法，提出一种组合式的RBF参数优化方法，但该方法仍存在过拟合的问题．

搜索者优化算法(seeker optimization algorithm, SOA)是一种基于人群的启发式搜索算法[14]，其全局搜索能力比粒子群优化(particle swarm optimization, PSO)算法强，且不易受局部极值的影响[15]．尽管有研究人员成功将SOA用于参数寻优和模型改进中[16-17]，但收敛速度慢和搜索精度低的缺陷仍令寻优结果不理想[18]．

此外，考虑到气象和时间等因素对建筑用电负荷的影响[19]，进行相似日选取可提升负荷预测模型的性能．吸引子传播(affinity propagation, AP)算法通过在待聚类对象之间传递相似度进行聚类[20]，与传统的k-means和模糊c均值聚类算法相比，AP算法参数设定简单，所有样本均参与竞争迭代，与目标对象的主要特征匹配更精准[7]．因此，本研究采用AP聚类算法分解样本空间，以期更准确的满足天气及日期类型的需求．

为提高利用RBF神经网络对大型公共建筑短期用电负荷预测的精度和速度，提出一种基于融合策略的改进人群搜索算法(fusion improvement seeker optimization algorithm, FISOA)，通过对传统SOA算法引入自适应速度因子，加快对RBF网络参数的寻优速度；采用多人协同搜索策略提高寻优效率；通过精英后代遗传策略降低解的随机性，并利用FISOA优化RBF神经网络的中心、宽度和权值．仿真实验结果显示，本研究所提基于AP相似日选取与FISOA-RBF神经网络模型(简称AP-FISOA-RBF模型)，能有效处理连续非线性动态规划问题，在预测精度和运行速度上均表现良好．

1 AP相似日理论

AP作为一种无监督聚类算法，能更快更优地处理大规模数据[21]．AP相似日理论的关键在于建立给定历史数据的相似性矩阵，并根据聚类特征获取历史负荷样本数据的相似日聚类结果．利用欧式距离定义任意两个样本Xi与Xj之间的相似度为

(1)

则所有样品的相似度构成相似度矩阵S．

AP算法通过在待聚类样本数据之间不断迭代代表矩阵R和归属矩阵A，并逐渐收敛至聚类中心[20]，每个聚类中心点即该类样本的代表. 第t次迭代时，样本点j适合作为样本点i的聚类中心的代表度Rt(i,j)为

(2)

其中，j′≠j, 表示除样本点j以外的其他样本点.因此，加入阻尼调节后实际的代表度Ract(t+1)为第t+1次迭代与第t次迭代的加权和，即

Ract(t+1)=(1-λ)Rt+1+λRt

(3)

At(i,j)为第t次迭代时， 样本点i选择样本点j作为聚类中心的合适程度即归属度，表达式为

(4)

其中，i′≠i, 表示除样本点i以外的其他样本点. 同样的，加入阻尼调节后实际的归属度Aact(t+1)的更新规则为

Aact(t+1)=(1-λ)At+1+λAt

(5)

其中，i为待聚类中心；λ为阻尼因子，λ∈(0, 1)默认λ=0.75． 决策矩阵为所有样本点的归属度矩阵A与代表度矩阵R的和．λ的引入可避免在迭代过程中产生数据振荡，保证决策矩阵的稳定收敛．当矩阵收敛时，将决策矩阵中的对角线元素大于0的数据点作为聚类中心，其余点按照决策矩阵中最大值所在位置依次分配到各个聚类中心[20]．

2 RBF神经网络

RBF神经网络作为3层反馈神经网络，基本结构包含n个神经元节点的输入层，m个节点的隐含层和k个节点的输出层[12]．RBF神经网络利用径向基函数作为单隐层空间的基，能将输入矢量X=[x1,x2, …,xn]T直接映射到隐层空间，并经隐层快速完成与输出层的线性映射，大大加快了RBF的学习速度并避免算法陷入局部最优，提高了非线性拟合能力，适用于具有复杂非线性特点的建筑用电负荷预测．隐含层H的第j个节点径向基函数是一个高斯函数，表达式为

(6)

其中，xi为第i个输入样本；cj为第j个网络节点中心；bj为第j个网络节点的网络基宽．网络输出Y=[y1,y2,…,yk]T中的第k个节点由隐层函数的线性加权和表示，即

(7)

其中，wjk为第j个隐层节点到第k个输出节点的权值．

3 SOA及其改进策略

3.1 SOA

SOA通过模拟人的智能搜索行为，寻求问题最优解[14]．算法以搜索队列为种群，根据智能群体的经验梯度和不确定推理行为，确定搜索方向和步长，进行适应度评价并完成位置更新，逐步逼近问题的最优解，实现问题的全局优化[22]．

3.1.1 搜索步长

采用线性隶属函数表示搜索步长模糊变量，结合文献[22]，设在最佳位置有最大隶属度值umax=0.900 0， 最差位置有最小隶属度umin=0.011 1． 适应度函数值i的隶属度ui和j维搜索空间适应度函数值i的隶属度ui， j分别为

(8)

ui, j=rand(ui,1),j=1,2,…,D

(9)

其中，s为种群规模；Ii为种群按适应度降序排列后的个体位置编号，I=1； rand()为随机数产生函数；D为问题维数．

由ui, j得到第j维空间的搜索步长为

(10)

其中，δi, j为高斯隶属度函数参数,δi, j=β|xmin-xmax|;xmin和xmax是同一种群中最小和最大函数值位置；惯性权值β跟随迭代过程从0.9线性递减至0.1，β=(tmax-t)/tmax;t和tmax为当前及最大迭代次数．αi, j在每迭代中都不小于0.

3.1.2 搜索方向

第i个搜寻个体的搜索方向di(t)由利己方向di,ego、利他方向di,alt和预动方向di,pro加权确定[20]，即

di(t)=sign(βdi,pro+φ1di,ego+φ2di,alt)

(11)

di,ego=pi,best-xi(t)

(12)

di,alt=gi,best-xi(t)

(13)

di,pro=xi(t1)-xi(t2)

(14)

其中， sign()为符号函数；φ1和φ2为[0, 1]内的常数；xi(t1)和xi(t2)分别为{xi(t-2),xi(t-1),xi(t)}中的前2名最佳位置；gi,best为第i个搜寻个体所在种群的集体历史最佳位置;pi,best为第i个搜寻个体到目前为止经历过的最佳位置．

3.1.3 位置更新

根据搜索方向和步长可实现位置的更新为

xi, j(t+1)=xi, j(t)+Δxi, j(t+1)

(15)

其中， Δxi, j(t+1)=ai, j(t)di, j(t);di, j(t)为第j维空间的第i个搜寻个体的搜索方向．

3.2 FISOA

3.2.1 自适应搜索改进

针对传统SOA收敛速度慢的问题，本研究提出的FISOA在搜索过程中，引入自适应搜索速度v及适应系数η， 以实现速度自适应，令SOA的迭代更新速度在数据量较大时，也能保持在良好水平．

第i个搜寻个体在j维空间里的速度适应过程为

vi, j(t+1)=ηvi, j(t)

(16)

(17)

其中，t为迭代次数；βmin和βmax分别为惯性权重最小值和最大值；f为当前位置的适应度；fmin和favg分别为适应度最小值和平均值．

3.2.2 搜索模式改进

传统SOA的单队列搜索模式严重影响搜索的效率和成功率，因此，本研究模拟人类的合作行为，提出一种多人协同搜索模式，通过将全体划分为多个子群体，使得在每一个子群体空间都能同时更新搜索步长、方向和速度，并根据适应度条件判断是否完成搜索．

设s为群体规模，l为每个子群体中的个体数，则子目标群体数g=s/l． 至此，可建立g×l维的解空间矩阵X=(xij)． 其中，i=1, 2, …,g;j=1, 2, …,l．

3.2.3 精英杂交策略

为提高SOA解空间的质量，本研究提出精英杂交遗传策略，以期能在最少的迭代次数中寻求最优解，令算法表现出更强的适应度，也获得较高的收敛精度．

首先，对局部最优解按照适应度由优至劣排序后记为P=[f1,f2, …,fl]， 取前k名组成“精英”，记为K=[f1,f2, …,fk]， 个体间的差异系数为

ε=|f(i+1)-fi|

(18)

其中，f(i+1)和fi分别为两个不同个体的适应度．

在算法迭代过程中，利用如式(19)的杂交因子α， 将保留的“精英”在杂交池中杂交g代，并用后代更替父代，以保持种群数目不变．

(19)

其中，fbest为最佳适应度值．可见， 个体间的差异系数ε越大，对精英后代的影响程度越大．

3.3 改进SOA算法性能测试

通过对传统SOA进行多策略融合改进，提出了改进后的FISOA寻优算法，具体步骤为：

1)设定迭代次数初始值t=0．

2)在可行解域随机产生s个初始位置．

3)子群体分配．将全体s划分为相互独立的g个子群体空间，每个子群体中包含l个个体，建立g×l维的子空间矩阵X．

4)在杂交池中按照式(18)和式(19)进行精英杂交并产生多组精英后代．

5)计算每个搜索位置的适应度值．

6)执行多人协同搜索策略，在各个子空间内，搜索者同时计算个体i在j维的搜索方向di, j(t)及步长αi, j(t)， 并根据自适应搜索速度vi, j(t)进行动态调整．

7)判断终止条件．当适应度或迭代次数达到设定值时跳出循环，并输出寻优结果；否则， 更新迭代次数并执行步骤2)．

采用3个典型测试函数Sphere、Schaffer和Rastrigin(函数表达式及参数设置请扫描论文末页右下角二维码查看表S1)对算法进行验证．记录PSO、SOA与FISOA算法对3个函数各运行50次后的平均最佳适应度值、平均收敛次数和达到最佳适应度的平均迭代次数，如表1，适应度迭代过程如图1所示．分析表1和图1可知，多数情况下 FISOA的性能比PSO和SOA算法表现更优，收敛曲线更平滑，收敛速度明显提高，同时具有更好的全局搜索性能，且适应度更强．

表1 采用PSO、SOA与FISOA算法对3个函数的测试结果

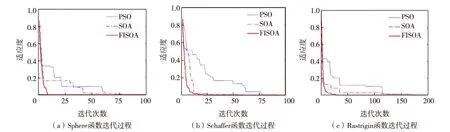
图1 PSO、SOA与FISOA算法在不同函数上的收敛性能Fig.1 (Color online) Algorithm convergence of PSO, SOA and FISOA

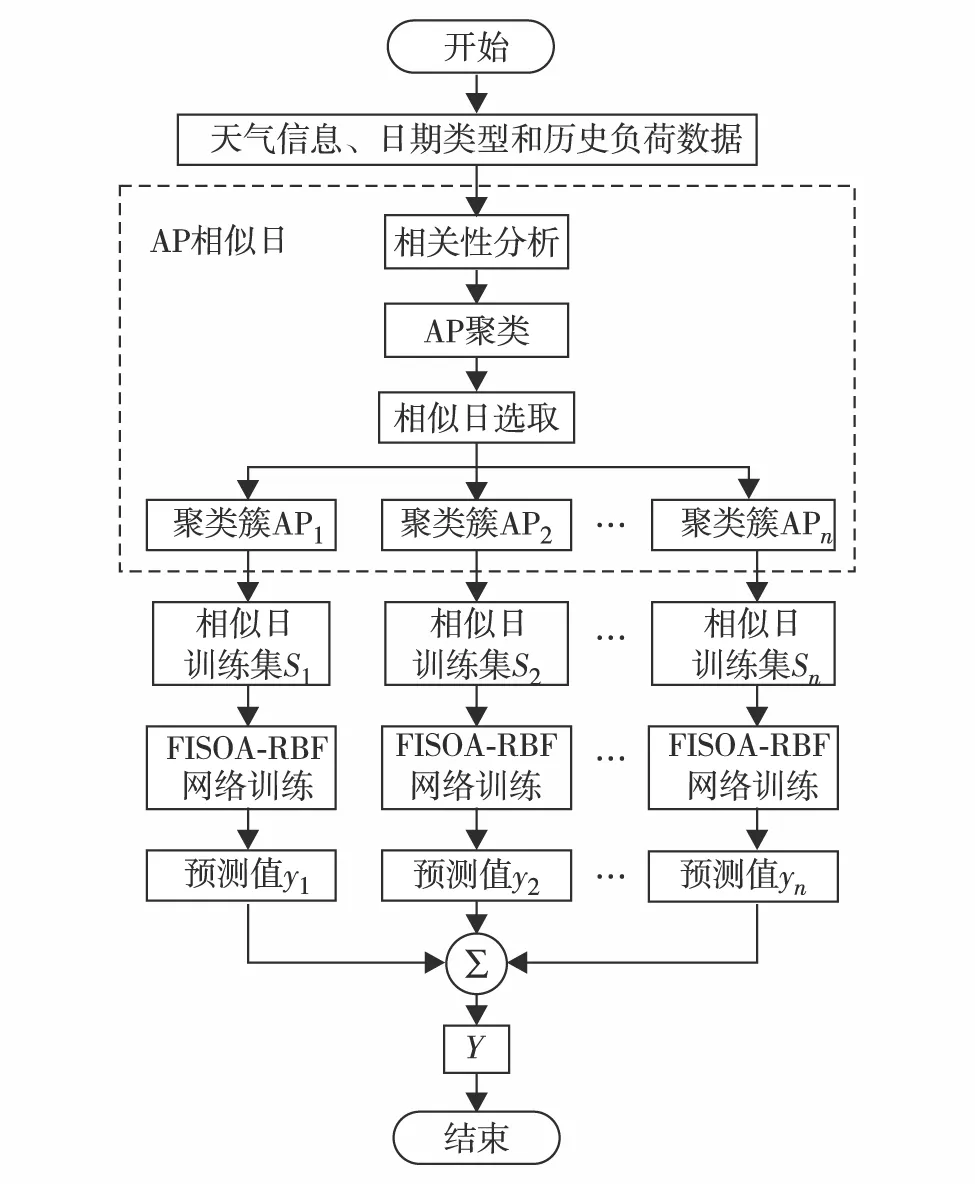
图2 AP-FISOA-RBF预测算法流程Fig.2 Flow chart of AP-FISOA-RBF forecasting algorithm

4 用电负荷预测模型

AP-FISOA-RBF模型的用电负荷预测算法流程如图2．首先，对天气信息、日期类型和历史负荷数据进行相关性分析，选取特征向量作为AP聚类的输入，获取AP聚类结果．然后，利用AP相似日理论，选取与预测日相关性较强的前n组AP聚类簇作为历史相似日，建立对应的FISOA-RBF神经网络相似日选取训练集并进行训练．最后，输出n个第i簇相似日预测值yi的加权求和结果Y作为最终实际预测值，即

(20)

其中，φi为预测权值，φi=ri/∑ri；ri为相关系数．

在算法迭代的过程中，以RBF神经网络的中心C、 宽度B和权值W建立初始搜索种群x=[c1b1w1c2b2w2…cmbmwm]， 寻求最小适应度下的最优解作为网络参数．以误差函数最小建立的适应度函数为

(21)

其中，Xi(t)和Ri(t)分别为第i次数据采集得到的电力负荷的预测值和实际值;n为预测时刻个数．

分析FISOA-RBF模型的适应度变化曲线(请描论文末页右下角二维码查看图 S1)可知，融合策略的引入，保持了随机解的稳定性，能够更快更准确地寻求RBF参数的全局最优解，使得RBF获得更好的学习速度和精度．

5 仿真实验结果与分析

以中国西安市某大型公共商业建筑为研究对象，采集2019-09-01—2019-10-21共1 224组用电负荷、日天气信息和日类型信息的标准化数据，并以2019-10-21为预测日，使用AP-FISOA-RBF模型仿真预测当天的用电负荷．其中，取前1 200组数据用于网络训练．预测模型的固定参数请扫描论文末页右下角二维码查看表S2，不同模型的参数训练方式请扫描论文末页右下角二维码查看表S3．

5.1 数据处理与特征向量

AP相似日选取的首要任务是选择合适的特征向量．首先，对天气和日期类型等定性指标进行数据量化，并归一化至[0, 1]．然后，利用皮尔逊系数法分析量化后的数据，获得影响建筑用电负荷的主要特征参数，如表2．选取系数较大的特征向量作为AP聚类与预测网络的输入，分别为历史日用电负荷(U1)、 日平均温度(U2)和日期类型(U3)， AP聚类的输出为AP簇(P)， 预测网络的输出为预测日用电负荷(Y)．

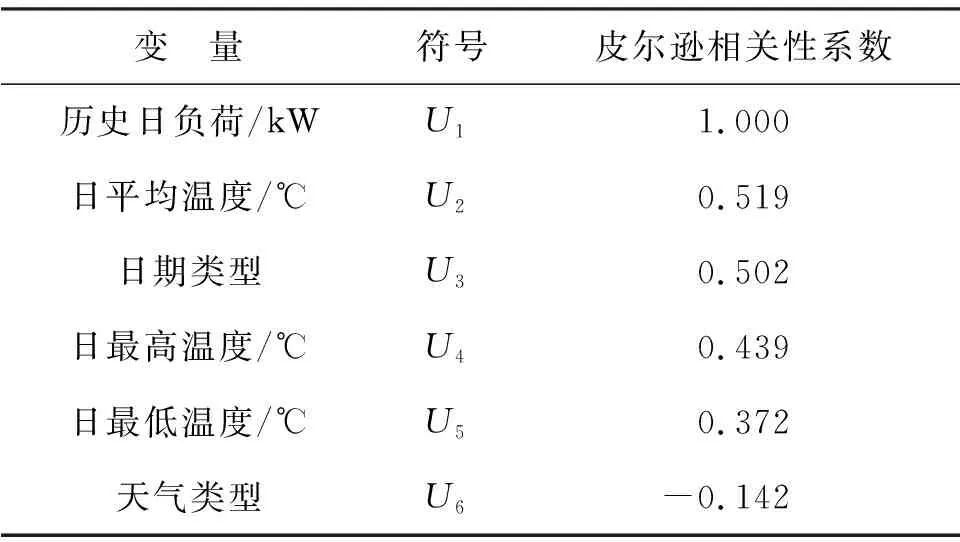
表2 负荷影响因素的相关性分析

5.2 AP相似日选取

AP相似日选取包括AP聚类与相似日的选取．输入历史日负荷、日平均温度和日期类型3个特征向量，采用AP算法进行聚类，结果如图3和表3,得到8组放射状AP聚类结果，同组聚类点之间具有显著相似性．相似日编号为[1, 2, …, 50]，分别代表历史日[2019-09-01, 2019-09-02, …, 2019-10-20]．

图3 AP聚类结果Fig.3 Result of AP clustering algorithm

将主要影响用电负荷的日平均温度(U2)和日类型(U3)作为2个特征向量，结合表3，利用皮尔逊系数法筛选与预测日相关性较高的前5组AP簇，即分别为AP8、AP7、AP1、AP6和AP3对应的相似日，从而完成相似日选取．

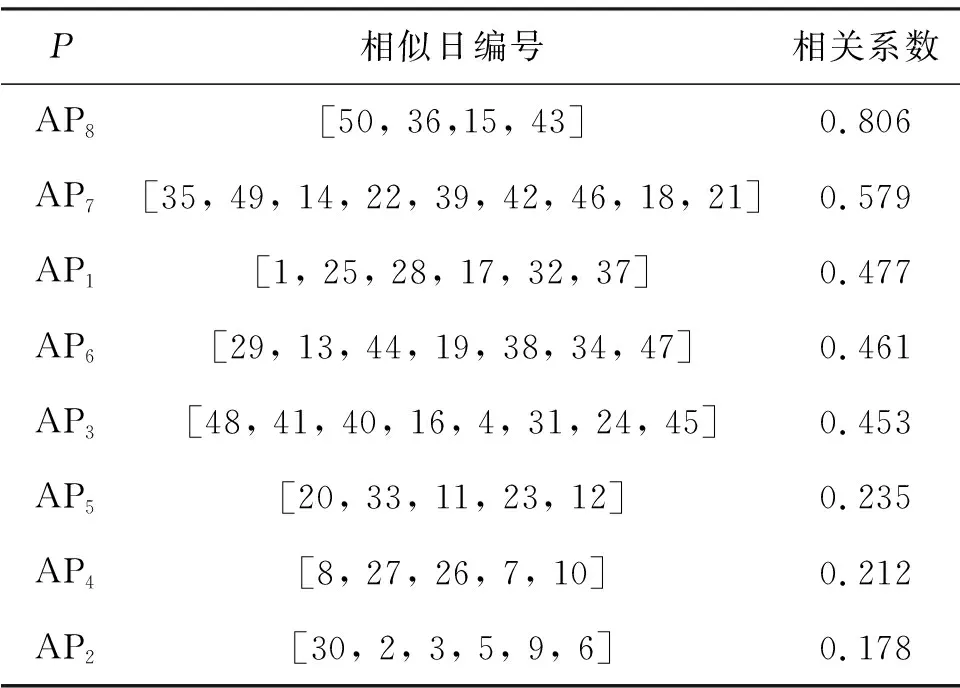
表3 AP聚类簇的相关性分析

5.3 模型评价指标

本研究采用平均绝对百分比误差(mean absolute percentage error, MAPE)和预测均方误差(mean square error, MSE)两个指标对预测模型进行评价，计算式分别为

(22)

(23)

其中，Xi和Ri分别为第i次采集数据的电力负荷的预测值和实际值；r为样品采集次数．预测模型的MAPE值越小表明模型的预测精度越好．

5.4 负荷预测及结果分析

本研究基于AP-FISOA-RBF模型预测2019-10-21的建筑物短期用电负荷．结合表2设置RBF神经网络为3-8-1结构，即网络输入层神经元个数n=3， 隐含层数目m=8， 输出层神经元个数k=1．结合表3，对AP8、AP7、AP1、AP6和AP3这5组AP相似日的数据进行训练，确定FISOA-RBF模型的相似日预测权值，计得实际预测值为

Y=0.28y1+0.21y2+0.17y3+

0.17y4+0.16y5

(24)

网络参数训练结果如表4．由表4可见，与传统RBF、SOA-RBF和PSO-RBF模型相比，训练后的AP-FISOA-RBF神经网络能够很好的逼近该非线性时间序列，逼近能力较高，也更易获得最佳运行效果下的最优解．

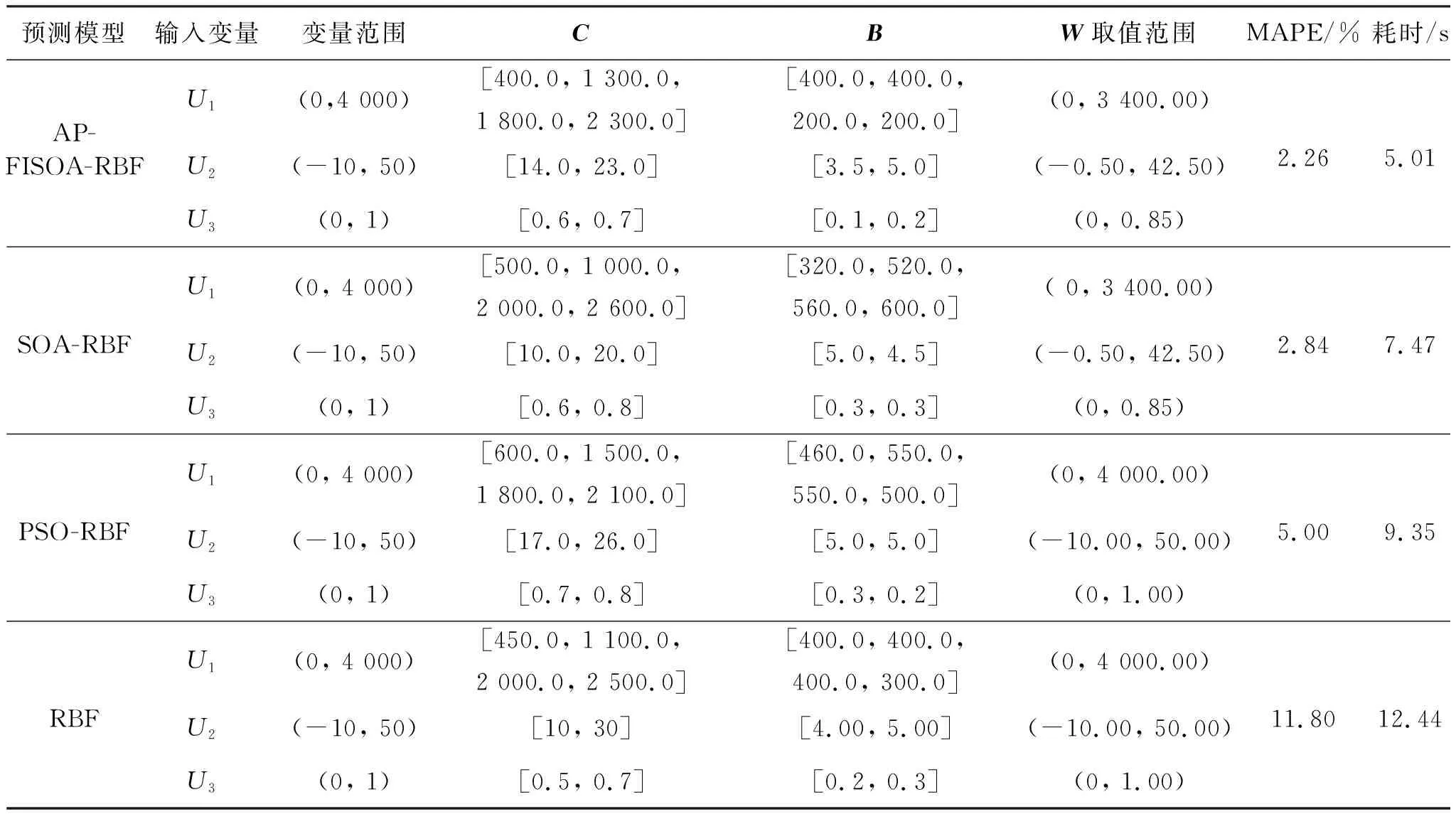
表4 网络训练参数及运行效果

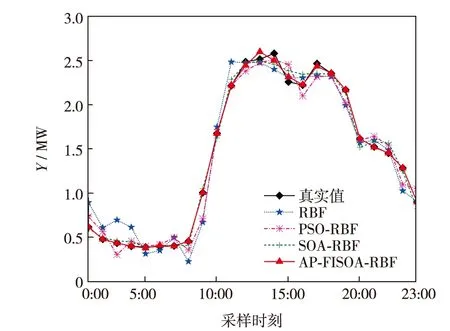
图4 RBF、PSO-RBF、SOA-RBF和AP-FISOA-RBF模型的建筑电力负荷日预测结果Fig.4 (Color online) Comparison of daily load forecasting results based on RBF、PSO-RBF、SOA-RBF、AP-FISOA-RBF mode

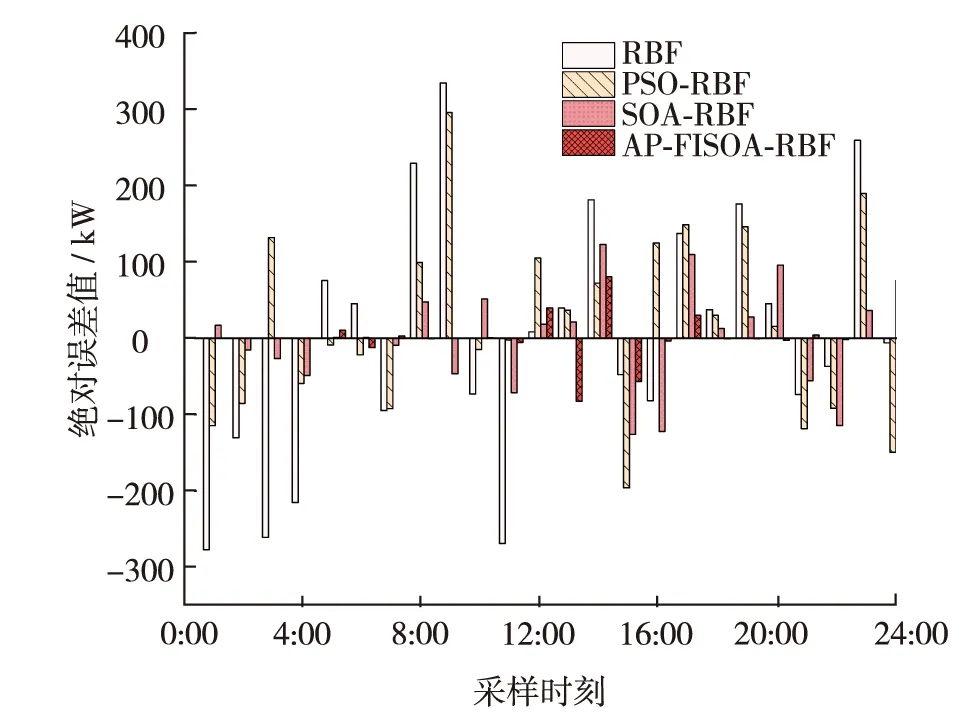
图5 建筑用电负荷日预测误差对比Fig.5 (Color online) Comparison of absolute errors of load forecasting

图4和图5为采用RBF、PSO-RBF、SOA-RBF和AP-FISOA-RBF算法进行建筑用电负荷预测的结果．可见，与传统的RBF、PSO-RBF和SOA-RBF预测模型相比，AP-FISOA-RBF模型的拟合度更高，预测结果更贴近真实值，MAPE值分别降低了93.05%、83.60%和71.13%，MSE值分别降低了95.30%、87.57%和73.23%．综上，采用融合策略改进后的FISOA 算法比常规PSO和SOA 算法性能更好，全局寻优性能更强，尤其是在对历史数据进行AP聚类处理后，可显著提升FISOA-RBF的预测精度．

采用聚类算法(k-means、模糊c-means和AP)和无聚类算法(AR、SVR、GM、RBF、PSO-RBF、SOA-RBF和FISOA-RBF)，计算建筑用电负荷预测的MAPE值、MSE值和模型运行的耗时，结果如表5．所有结果都是运行10次后的平均值．

分析表5可知，无聚类算法处理下，RBF模型的MAPE值比其他采用单一算法模型更小，即预测结果更稳定，证明采用RBF神经网络的合理性．其中，FISOA-RBF模型的预测误差最小，更贴近真实值．可见，融合改进策略能够使FISOA算法更好地优化RBF网络参数，弥补了梯度下降法进行参数调整的不足，提高了传统RBF的预测性能．采用AP聚类后，AP-FISOA-RBF模型预测的MAPE低至0.82%，MSE低至805.17 kW2，比无聚类算法的FISOA-RBF模型降低了68.05%，明显减少了外界环境对负荷预测的影响，增强了模型的稳定性．但是，k-means和模糊c-means算法因初始聚类中心及聚类数难以设定，预测时长和误差均显著增加．

分析模型运行耗时结果发现，虽然传统的RBF模型的预测时间较长，但优化后训练速度均能得到显著提高，AP-FISOA-RBF模型的平均预测速度比传统RBF、PSO-RBF和SOA-RBF模型分别提高了54.34%、39.25%和23.96%，收敛速度显著提高．

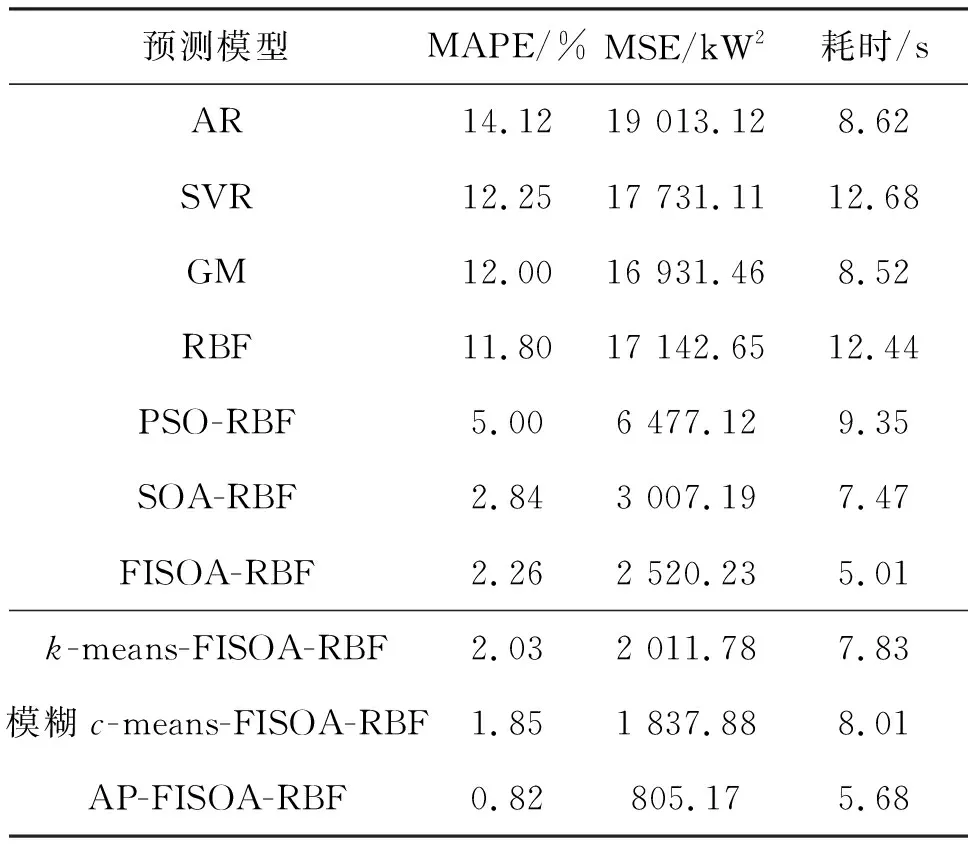
表5 不同模型的预测性能

结 语

结合SOA算法的全局搜索性能，改进后的FISOA算法可对RBF网络的中心、权值和宽度参数进行更准确有效的全局寻优．同时，AP相似日选取的应用能有效克服天气和日期类型等影响，快速且准确地处理大量样本数据．相比传统的PSO和SOA算法，采用融合策略的FISOA算法能明显优化RBF网络．自适应搜索速度和多人协同搜索模式显著加快了对RBF参数的寻优速度，精英后代遗传策略明显降低了子代种群的随机性，提高了解的质量．综上可见，本研究提出的AP-FISOA-RBF预测模型受输入影响较小，在预测精度和收敛速度上均有较好的表现，证明了模型在高精度用电负荷预测方面的有效性和可靠性．